中考数学压轴题12讲

目录
第1讲因动点产生的相似三角形问题
第2讲因动点产生的等腰三角形问题
第3讲因动点产生的直角三角形问题
第4讲因动点产生的平行四边形问题
第5讲因动点产生的面积问题
第6讲因动点产生的相切问题
第7讲因动点产生的线段和差问题
第8讲由比例线段产生的函数关系问题
第9讲代数计算及通过代数计算进行说理问题
第10讲图形的平移
第11讲图形的翻折
第12讲图形的旋转
第1讲因动点产生的相似三角形问题
课前导学
相似三角形的判定定理有3个,其中判定定理1和判定定理2都有对应角相等的条件,
因此探求两个三角形相似的动态问题,一般情况下首先寻找一组对应角相等
判定定理2是最常用的解题依据,一般分三步:寻找一组等角,分两种情况列比例方程,
解方程并检验
如果已知∠A=∠D,探求△ABC与△DEF相似,只要把夹∠A和∠D的两边表示出来
按照对应边成比例,分
AB
DE
AB
DE
两种情况列方程
应用判定定理1解题,先寻找一组等角,再分两种情况讨论另外两组对应角相等
应用判定定理3解题不多见,根据三边对应成比例列连比式解方程(组)
还有一种情况,讨论两个直角三角形相似,如果一组锐角相等,其中一个直角三角形的
锐角三角比是确定的,那么就转化为讨论另一个三角形是直角三角形的问题,
求线段的长,要用到两点间的距离公式,而这个公式容易记错.理解记忆比较好
如图1,如果已知A、B两点的坐标,怎样求A、B两点间的距离呢?
我们以AB为斜边构造直角三角形,直角边与坐标轴平行,这样用勾股定理就可以求斜
边AB的长了,水平距离BC的长就是A、B两点间的水平距离,等于A、B两点的横坐标相
减:竖直距离AC就是A、B两点间的竖直距离,等于A、B两点的纵坐标相减
图1
例1
2014年湖南省衡阳市中考第28题
次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(-3,0)、B(1,O)两点,与y轴交于
点C(0,-3m)(m>0),顶点为D.
(1)求该二次函数的解析式(系数用含m的代数式表示)
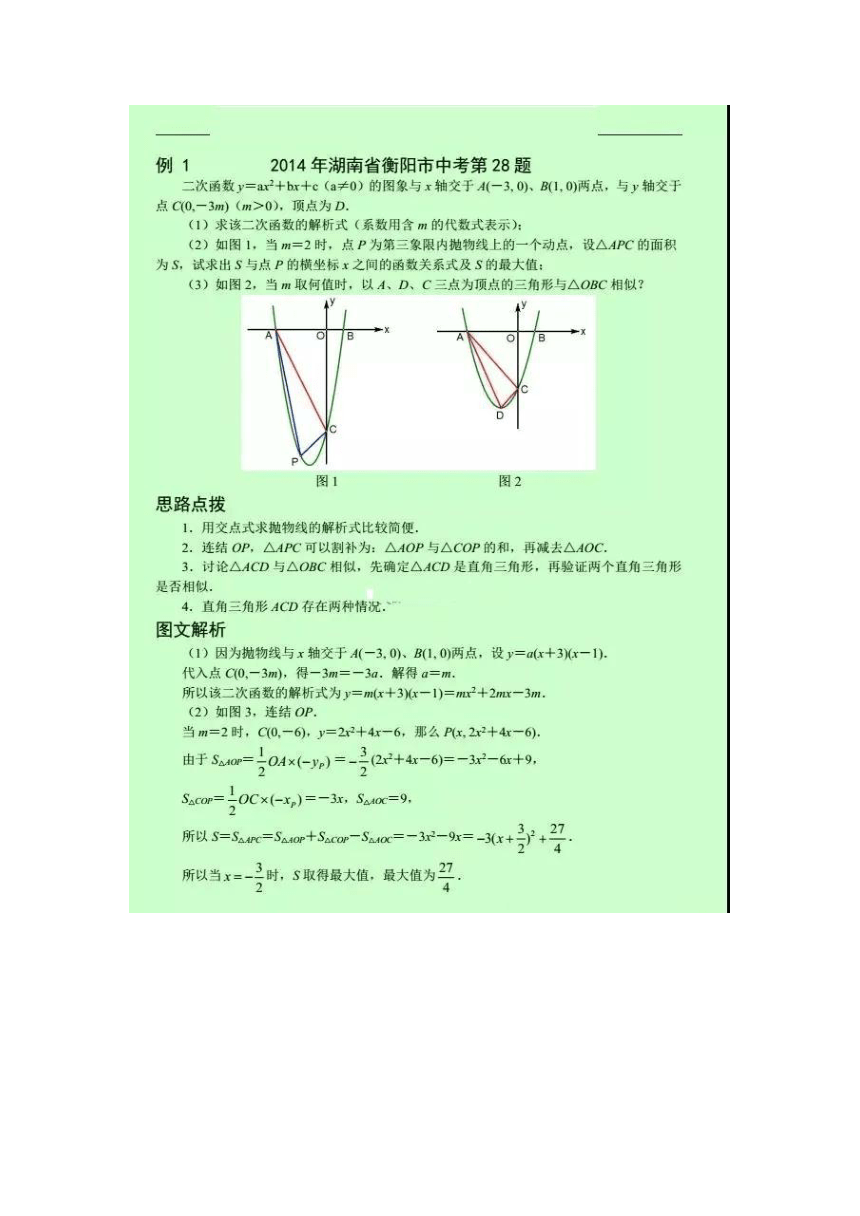
(2)如图1,当m=2时,点P为第三象限内抛物线上的一个动点,设△APC的面积
为S,试求出S与点P的横坐标x之间的函数关系式及S的最大值
(3)如图2,当m取何值时,以A、D、C三点为顶点的三角形与△OBC相似?
图2
思路点拨
1.用交点式求抛物线的解析式比较简便
2.连结OP,△APC可以割补为:△AOP与△COP的和,再减去△AOC.
3,讨论△ACD与△OBC相似,先确定△ACD是直角三角形,再验证两个直角三角形
是否相似
4.直角三角形ACD存在两种情况.
图文解析
(1)因为抛物线与x轴交于A(-3,0)、B(1,0)两点,设y=a(x+3)x-1)
代入点C(0,-3m),得-3m=-3a.解得a=m,
以该二次函数的解析式为y=m(x+3)x-1)=mx2+2mx-3m
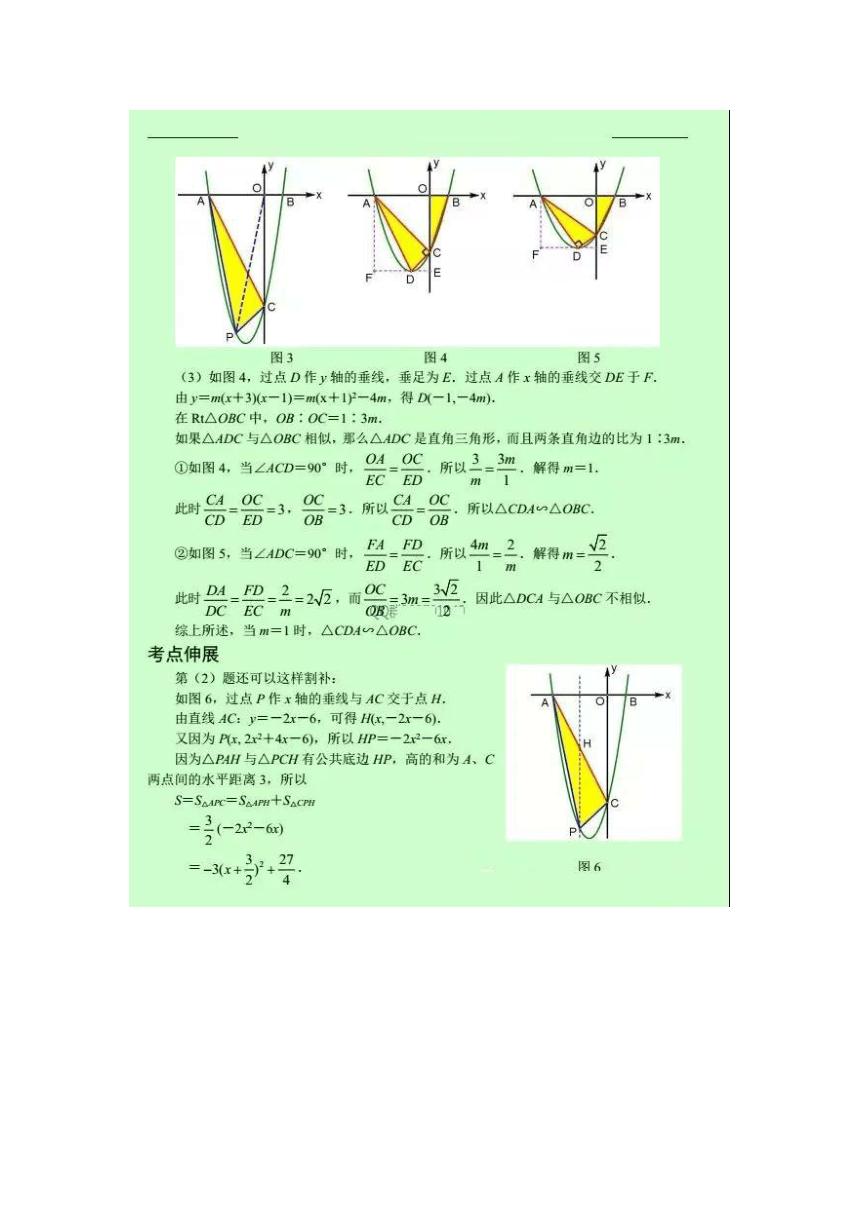
(2)如图3,连结OP
当m=2时,C(0,-6,y=2x2+4x-6,那么P(x,2x2+4x-6)
-3x,
S
所以S=Sw=S+32cm-S△=-3x2-9x=_,3:,27
所以当x=2时取得最大值,最大值为