初中数学二级结论（pdf版）

公式及其变式
(x+ax+b)
(a+b)x+ab
a2+b2=(a+b)2-2ab=(a-b)2+2ab
(a+b)+(a-b)
)2(a+b)2-(a2+b2)(a-b)2-(
4
3、和的立方公式:(a+b)=a3+3a2b+3b2+b3
差的立方公式:(a-b)=a2-3ab+3a
4、立方和公式:a3+b3=(a+b)a2-ab+b2)
变式a4+b2=(a+b)a+b2-3m
5、立方差公式:a3-b3=(a-b)a2+ab+b2)
变式
b3=(a-b)ka-b)2+3
注意区别:(a+b+c)=a2+b2+a2+2ab+2be+2ac
(a+b)+(b+c)2+(a+c)2=2a2+2b2+2c2+2ab+2bc+2
6.
a+6+c-3abc
=(a+6+cXa+62+c2-ab-bc-ac)
(a+b+c)
(a-b)+(b-c)2+(a-c)
二、数学计算中的常用结论
1、1+2+3+…+n=m(n+1
2
2、2+4+6+…+2Hn=1(n+1)
3、1+3+5+7+…+(2H-1)=n
4、12+2+32+42+…+n2=mn+)(2n+1
43
(1+2+3
6、1×2+2×3+3×4+4×5+…+m(n+1)=2+(n+2
k
n(n+h)
nn+k
a+b11
b
常见几何基本图形及结论:
1、∠ADC=∠A+∠B+∠C
2、BD,CD分别平分∠ABC,∠ACB,则∠BDC=90°+
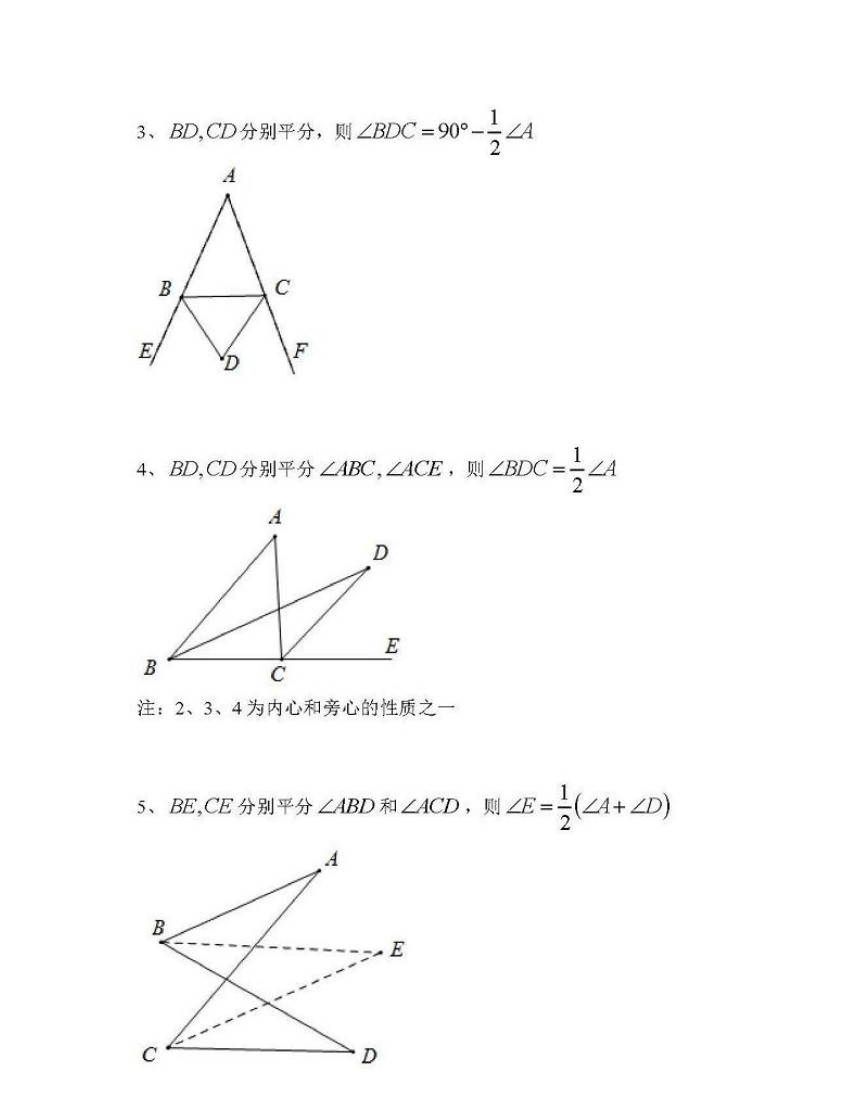
3、BD,CD分别平分,则∠BDC=90°-∠4
4、BD、CD分别平分∠ABC,∠ACE,则∠BDC=∠A
A
注:2、3、4为内心和旁心的性质之
5、BE,CE分别平分∠BD和∠ACD,则EE=(∠4+∠D)
E
C
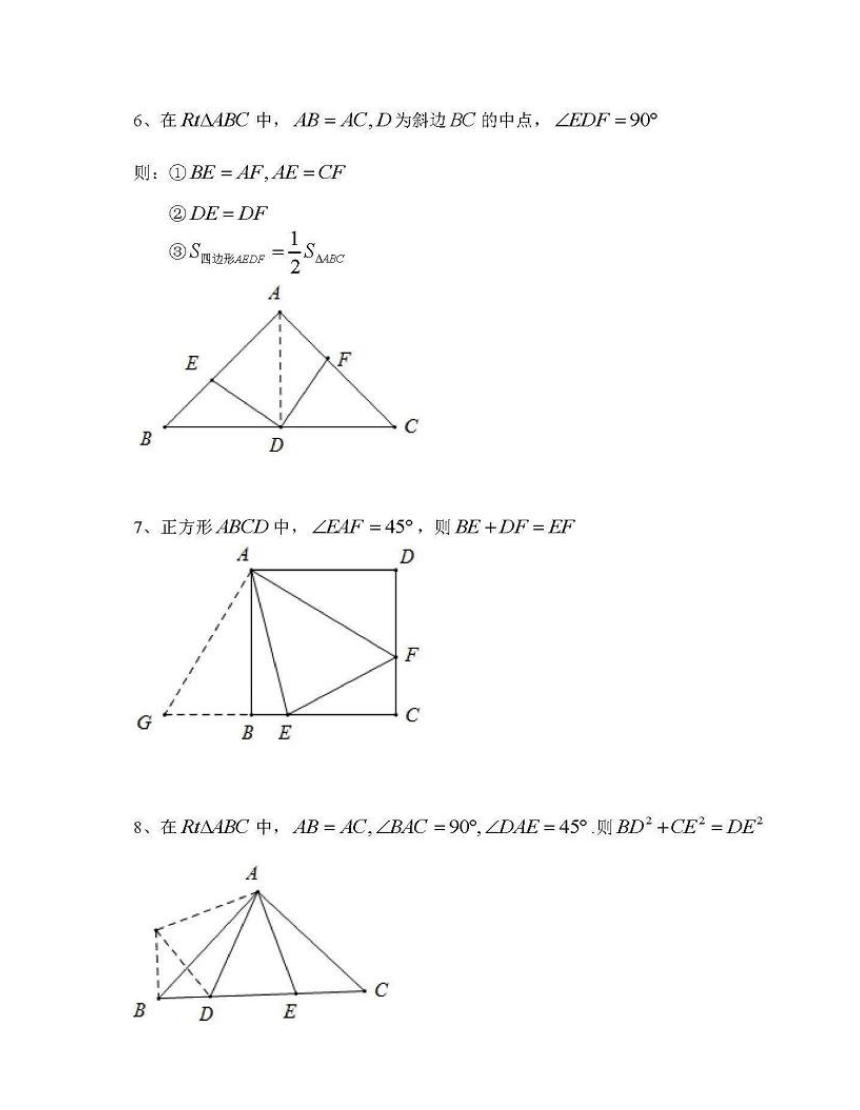
6、在RMBC中,AB=AC,D为斜边BC的中点,∠EDF=90°
则:①BE=AF,AE=CF
②DE=DF
四边形AEDF
E
7、正方形ABCD中,∠EAF=45°,则BE+DF=EF
B
E
、在R△BC中,AB=AC,∠BAC=90°,∠DAE=45°则BD2+CE2=DE2
B
D
E
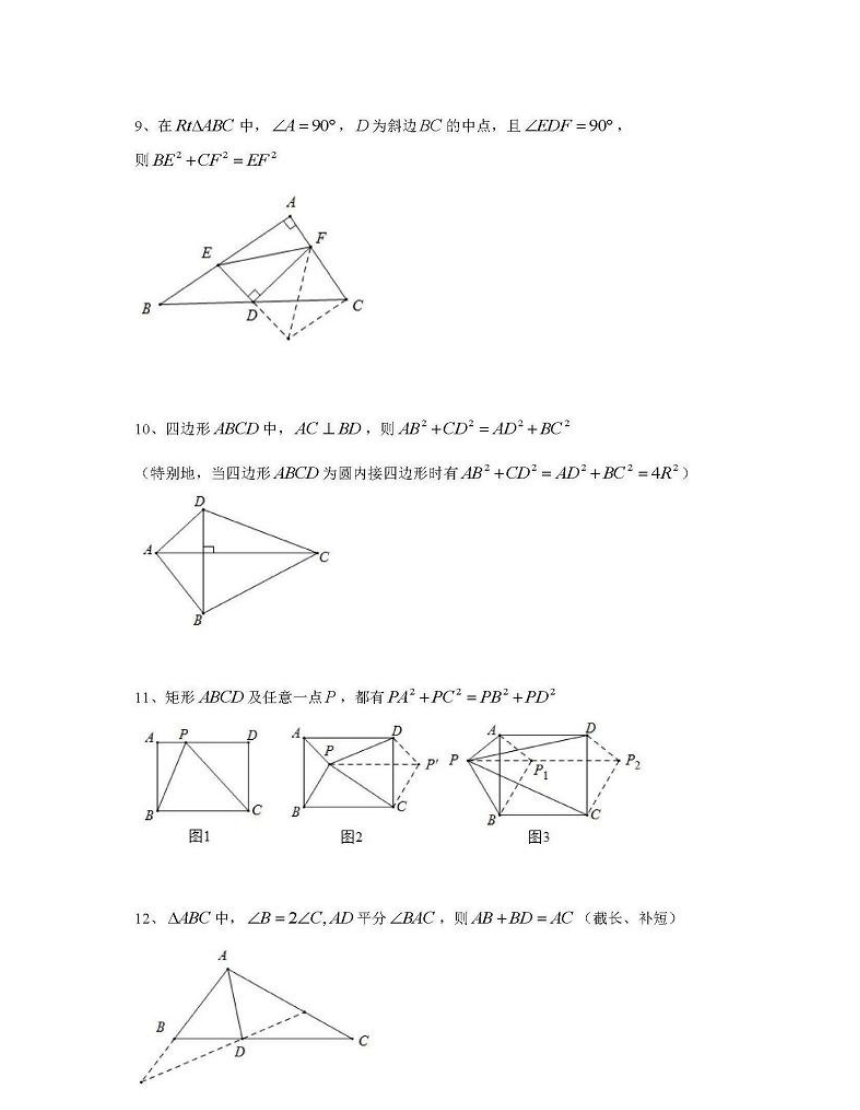
9、在R△ABC中,∠A=90°,D为斜边BC的中点,且∠EDF=90°
BE
+CF2=EFZ
10、四边形ABCD中,AC⊥BD,则AB2+CD2=AD2+BC2
(特别地,当四边形ABCD为圆内接四边形时有AB2+CD2=AD2+BC2=4R2)
11、矩形ABCD及任意一点P,都有PA2+PC2=PB2+PD2
12、△ABC中,∠B=2∠C,AD平分∠BC,则AB+BD=AC(截长、补短)
A
B