人教版八年级数学下册 18.1.1平行四边形的性质 课件(共19张ppt)
文档属性
| 名称 | 人教版八年级数学下册 18.1.1平行四边形的性质 课件(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 204.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 09:29:59 | ||
图片预览



文档简介
(共19张PPT)
任画一个三角形,如果平移两边后,得到一个什么图形?
A
B
C
18.1.1平行四边形
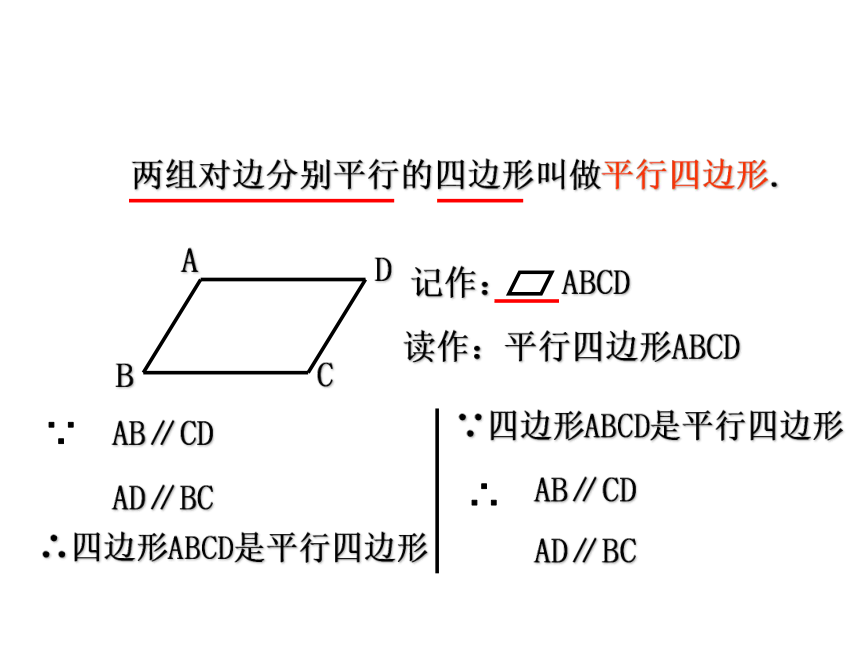
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作:
ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
画一画
请在草稿纸上任意画一个平行四边形
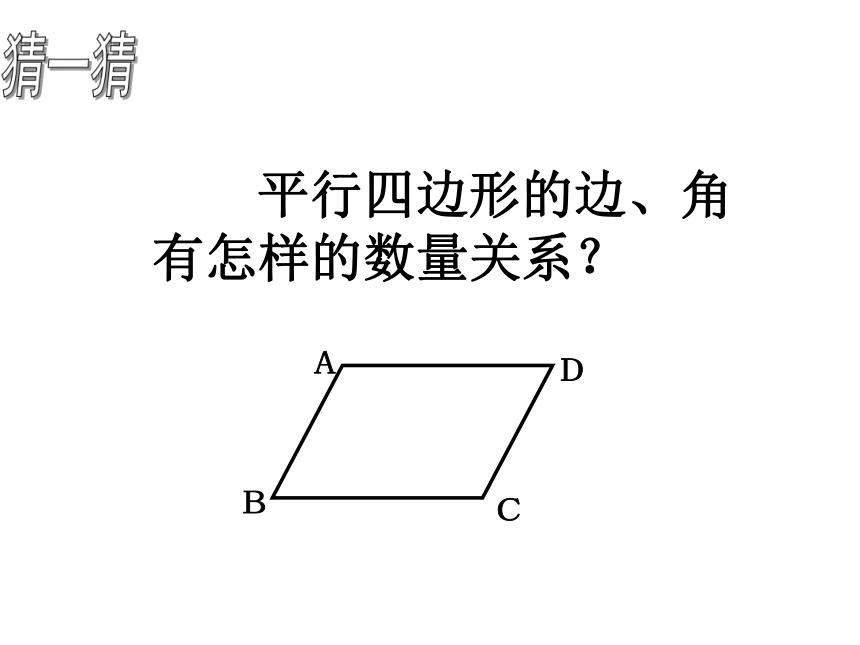
平行四边形的边、角有怎样的数量关系?
A
B
C
D
猜一猜
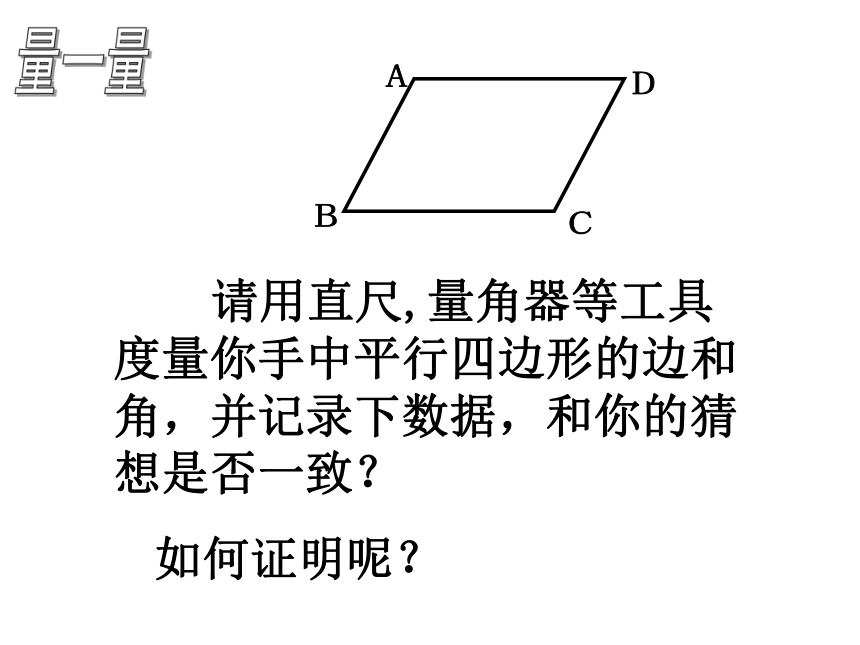
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,和你的猜想是否一致?
量一量
A
B
C
D
如何证明呢?
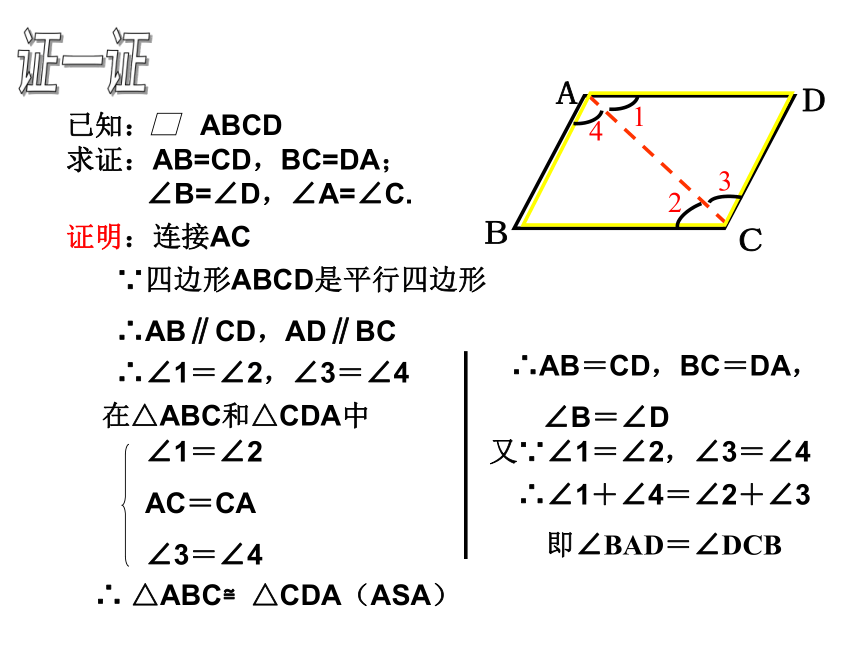
已知:
ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
证一证
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴
△ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的性质
几何语言:
定理1:平行四边形的对边相等
定理2:平行四边形的对角相等
∵
四边形ABCD是平行四边形
∴
AB=CD,AD=BC.(平行四边形的对边相等)
∠B=∠D,∠A=∠C
.(平行四边形的对角相等)
思考:平行四边形的邻角有什么关系呢?
平行四边形的邻角互补
D
A
B
C
F
E
例1:如图,在
ABCD中,DE垂直于AB,BF垂直于CD,垂足分别为E,F。求证:AE=CF。
H
A
B
C
D
G
若a
//
b,作
AD
//
GH
//
BC,分别交
b于D、H、C,交
a于A、G、B.
两条平行线间的距离
则
GH=AD=BC.
两条平行线之间的平行线段相等
则
DA
HG
CB.
若a
//
b,DA、GH、CB垂直于
a,交a于A、G、B,交
b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
1、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
A
B
C
D
⑵
若∠A+∠C=200°,
则∠A和∠B分别为多少度?
⑴
其他三条边各长多少?
A
B
D
C
F
E
2.已知
ABCD,延长AB到E,
延长CD到F
,使BE=DF
求证:AF=CE
练习
1.在
ABCD中,
AB=3cm,BC=8cm,则 ABCD的周长
是
cm.
2. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3.
ABCD的周长为30cm,AB比BC长5cm,则AB=
cm,
CD=
cm.
22
10cm,5cm
10
10
4、在
ABCD中,外角38°,则四个内角的度数分别是:
????????????
142°,38°,142°,38°
2.如图,在
ABCD中,∠B的平分线BE交AD于E,BC=5,AB=3,则ED的长为
.
2
∠BCD的平分线交AD于点F,则EF长_________
F
1
CF与BE位置关系呢?
垂直
课堂练习(提高题)
证明题
1、如图(1),△ABC中,AB=AC.D、E、F分别在BC、AB、AC上,且四边形AEDF是平行四边形.求证:DE+DF=AB.
2、如图(2),四边形ABCD与EBFD均是平行四边形.求证:AE=CF.
A
B
C
D
E
F
(1)
(2)
A
B
C
D
E
F
课堂小结
通过本节课的学习,你有哪些收获?
1.平行四边形的概念
两组对边分别平行的四边形叫做平行四边形
2.平行四边形的性质及应用
边:平行四边形的对边平行且相等
角:平行四边形的对角相等,邻角互补。
作业
课本43页:练习第1、2题
课本49页:
习题18.1复习巩固
第1、2题
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
任画一个三角形,如果平移两边后,得到一个什么图形?
A
B
C
18.1.1平行四边形
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作:
ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
画一画
请在草稿纸上任意画一个平行四边形
平行四边形的边、角有怎样的数量关系?
A
B
C
D
猜一猜
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,和你的猜想是否一致?
量一量
A
B
C
D
如何证明呢?
已知:
ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
证一证
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴
△ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的性质
几何语言:
定理1:平行四边形的对边相等
定理2:平行四边形的对角相等
∵
四边形ABCD是平行四边形
∴
AB=CD,AD=BC.(平行四边形的对边相等)
∠B=∠D,∠A=∠C
.(平行四边形的对角相等)
思考:平行四边形的邻角有什么关系呢?
平行四边形的邻角互补
D
A
B
C
F
E
例1:如图,在
ABCD中,DE垂直于AB,BF垂直于CD,垂足分别为E,F。求证:AE=CF。
H
A
B
C
D
G
若a
//
b,作
AD
//
GH
//
BC,分别交
b于D、H、C,交
a于A、G、B.
两条平行线间的距离
则
GH=AD=BC.
两条平行线之间的平行线段相等
则
DA
HG
CB.
若a
//
b,DA、GH、CB垂直于
a,交a于A、G、B,交
b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
1、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
A
B
C
D
⑵
若∠A+∠C=200°,
则∠A和∠B分别为多少度?
⑴
其他三条边各长多少?
A
B
D
C
F
E
2.已知
ABCD,延长AB到E,
延长CD到F
,使BE=DF
求证:AF=CE
练习
1.在
ABCD中,
AB=3cm,BC=8cm,则 ABCD的周长
是
cm.
2. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3.
ABCD的周长为30cm,AB比BC长5cm,则AB=
cm,
CD=
cm.
22
10cm,5cm
10
10
4、在
ABCD中,外角38°,则四个内角的度数分别是:
????????????
142°,38°,142°,38°
2.如图,在
ABCD中,∠B的平分线BE交AD于E,BC=5,AB=3,则ED的长为
.
2
∠BCD的平分线交AD于点F,则EF长_________
F
1
CF与BE位置关系呢?
垂直
课堂练习(提高题)
证明题
1、如图(1),△ABC中,AB=AC.D、E、F分别在BC、AB、AC上,且四边形AEDF是平行四边形.求证:DE+DF=AB.
2、如图(2),四边形ABCD与EBFD均是平行四边形.求证:AE=CF.
A
B
C
D
E
F
(1)
(2)
A
B
C
D
E
F
课堂小结
通过本节课的学习,你有哪些收获?
1.平行四边形的概念
两组对边分别平行的四边形叫做平行四边形
2.平行四边形的性质及应用
边:平行四边形的对边平行且相等
角:平行四边形的对角相等,邻角互补。
作业
课本43页:练习第1、2题
课本49页:
习题18.1复习巩固
第1、2题
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
