人教版七年级数学上册 4.3 角 课件(共68张ppt)
文档属性
| 名称 | 人教版七年级数学上册 4.3 角 课件(共68张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 00:00:00 | ||
图片预览






文档简介
(共68张PPT)
4.3
角
4.3.1
角
角的两种定义和四种表示方法;
角度制的定义和度量单位之间的相互转换.
学习目标
房顶的角
剪刀的角
圆规的角
楼梯的折角
时针和分针的夹角
棱锥上的角
三角尺上的角
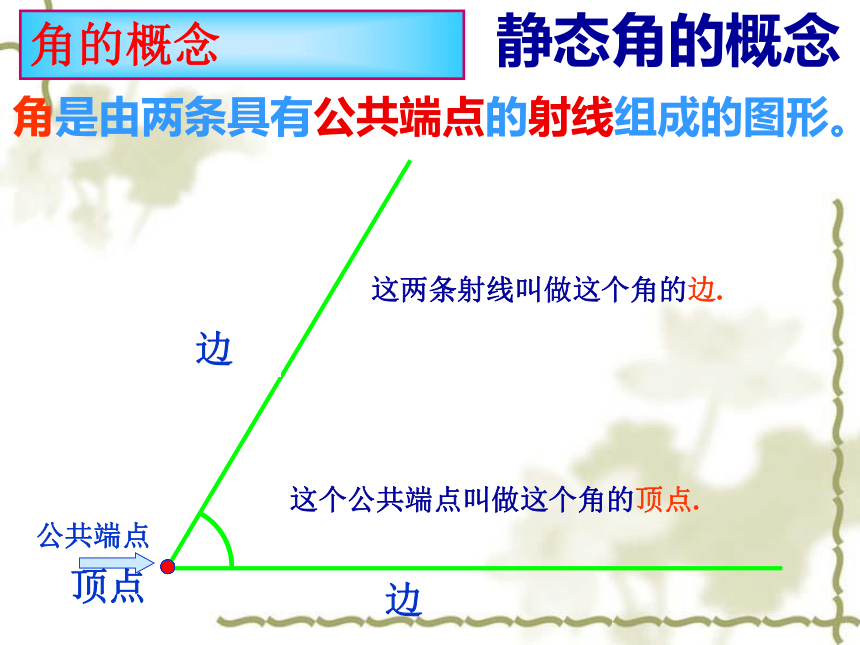
角是由两条具有公共端点的射线组成的图形。
公共端点
顶点
射线
射线
边
边
静态角的概念
角的概念
这个公共端点叫做这个角的顶点.
这两条射线叫做这个角的边.
(
)
(
)
(
)
(
)
(
)
(
)
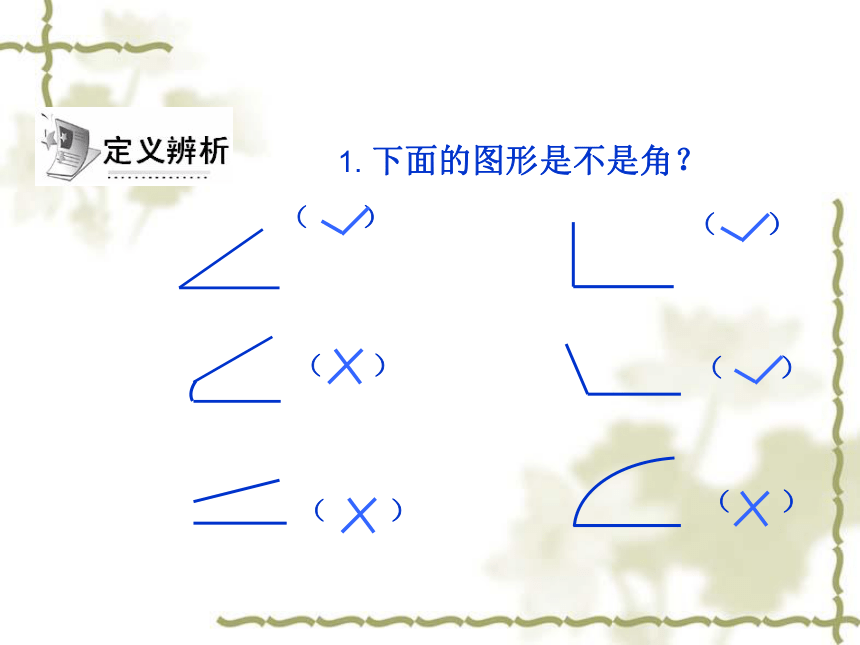
1.
下面的图形是不是角?
(1)两条直线组成一个角。
(
)
(2)两条射线组成一个角。
(
)
(3)具有公共端点的两条射线组成一个角
。(
)
(4)角的边画得越长,角就越大。
(
)
2.判断下列说法是否正确。
1
2
3
4
5
6
7
8
9
10
11
12
时针和分针的夹角
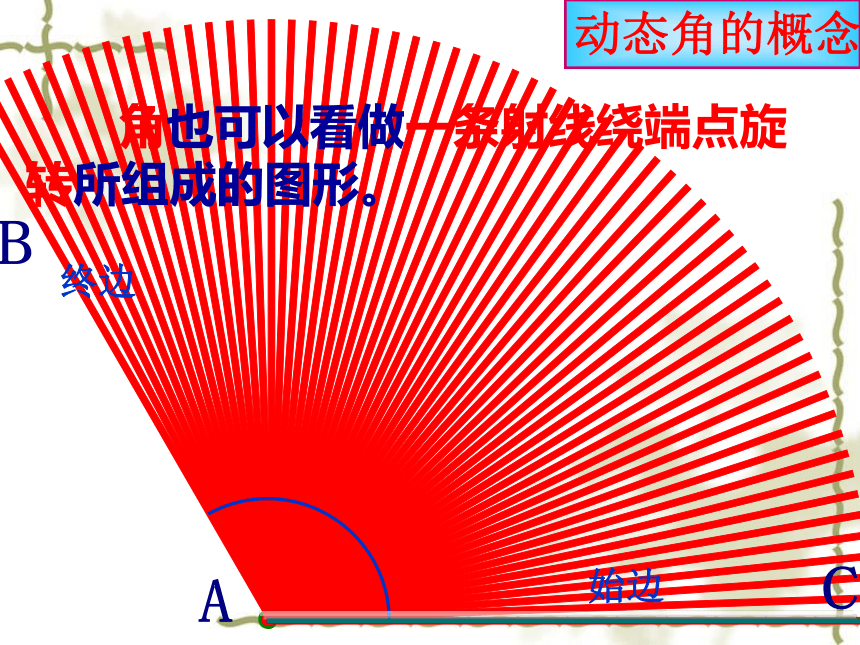
C
A
B
角也可以看做一条射线绕端点旋转所组成的图形。
动态角的概念
终边
始边
O
A
B
如果一个角的终边旋转到与始边成一条直线时,所成的角叫做平角。
认识平角
B
O
A
(B)
当终边继续旋转,旋转到与始边重合时,所成的角叫做周角。
认识周角
B
在不做特别说明的情况下,我们说的角都指不大于平角的角
角的表示方法
角用“∠”表示,读做“角”。角的表示方法有下面几种:
A
B
C
如:∠ABC
或∠CBA
(1)表示:
(2)
用角的顶点字母表示:
如:∠B
A
B
C
D
这里能用∠
B表示角吗?
(顶点字母写在中间)
(只有一个角时)
角的表示方法
如:∠1、∠2
(3)
用一个数字表示:
A
B
C
D
1
2
A
B
C
D
β
α
如:∠α、∠
β
(4)也可用一个希腊字母表示:
角的表示
角用符号“∠”来表示.
(1)用三个大写字母表示,三个字母应分别写在顶点及两边上的点,顶点的字母必须写在中间.
(2)角也可用一个大写字母表示,这个字母写在顶点处,它只适用于顶点处只有一个角.
∠O
∠AOB
或∠BOA
表示的是同一个角
(3)用一个数字加弧线表示.
1
α
(4)用一个小写希腊字母加弧线表示.
∠1
∠
α
O
A
O
B
试一试
1.把图中的角表示成下列形式:
①∠APO
②∠AOP
③∠OPC,
④∠O
⑤∠COP
⑥∠P。
其中正确的有
(把你认正确的序号都填上。)
P
O
A
C
①
③
⑥
你会了吗?
将图中的角用不同的方法表示出来,并填写下表:
A
D
B
C
E
1
2
α
∠1
∠ACB
∠BAC
∠
β
β
∠ABC
∠BCE
∠α
∠2
∠BAD
∠B
把圆周分成360等分,每一份所对的角叫做
。
记作
“
”
。
把1度的角60等分,每一份所对的角叫做
1
分角。
记作
“
1
′
”
。
把1分的角60等分,每一份所对的角叫做
1
秒角。
记作
“1″
”
。
1度角
1°
以度,分,秒为单位的角的度量制叫做角度制。
角的度量单位:度
、分、秒.
度
分
秒
×60
×60
×3600
÷60
÷3600
÷60
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″
例1
填空
72036/
=
0
解:(1)72036/=720+36/
=720+(36÷60)0
=720+0.60
=72.60
(2)38.170=380+0.17
0
=380+(0.17
×60)/
=380+10/+0.2/
=380+10/+(0.2
×60)//
=380
+10/+12
//
=38010/
12
//
1.用度、分、秒表示:
⑴0.75°= ′= ″
⑵(-)°= ′= ″
⑶16.24°= ° ′ ″
⑷34.37°= ° ′ ″
4
15
45
2700
16
960
16
14
24
34
22
12
练习
小结
1.角的定义一:
有公共端点的两条射线组成的图形
叫做角,这个公共端点叫做角的顶点,这
两条射线叫做角的边。
2.角的定义二:
角可以看成是一条射线绕着它的
端点从一个位置旋转到另一个位置所形成
的图形。射线旋转时经过的平面部分叫角
的内部。
角的表示
角用符号“∠”来表示.
(1)用三个大写字母表示,三个字母应分别写在顶点及两边上的点,顶点的字母必须写在中间.
(2)角也可用一个大写字母表示,这个字母写在顶点处,它只适用于顶点处只有一个角.
∠O
∠AOB
或∠BOA
表示的是同一个角
(3)用一个数字加弧线表示.
1
α
(4)用一个小写希腊字母加弧线表示.
∠1
∠
α
O
A
O
B
5、角的度量单位:度
、分、秒.
度
分
秒
×60
×60
×3600
÷60
÷3600
÷60
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″
4.3.2
角的比较与运算
角的两种比较大小的方法;
会计算角度的和差,能理解两个角的和、差、的意义.
学习目标
问题:有一天学生张虎和王鹏各带了一把折扇(如图),下面是他们的一段对话:
张:我的折扇大一些,所以我的折扇的角
也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
同学们,你们有办法帮他们进行判断吗?
A
B
C
D
E
F
怎样比较∠ABC和∠DEF的大小?
知识回顾:线段的比较方法
1.以“数”
出发,通过度量长度进行数值大
小比较。
度量法
以“数”
出发,通过度量长度,长度大的线段也大。
5
cm
A
B
3
cm
C
D
AB
>
CD
2.从“形”出发,利用线段移动叠合的方法
A
B
A
C
叠合法
叠合
A
(
C
)
A
C
A
B
C
A
A
B
A
B
(AB
>
AC)
(AB
=
AC)
(AB
<
AC)
一,角的比较:
请同学们任意画出两个角比较一下,并讨论你们的比较方法:
B
A
C
E
D
F
你的方法有:
(1)度量法比较
(2)叠合法比较
45°
60°
A
o
B
D
E
F
度量法
所以:∠AOB<∠DEF
读数为45
读数为60
ED落在∠ABC的外部,则∠DEF
>
∠ABC。
把∠DEF移动,使它的顶点E和∠ABC的顶点B重合,一边EF和BC重合,另一边ED和BA落在BC的同旁。
A
B
C
D
E
F
(
)
(
)
比较∠ABC
和
∠DEF的大小
叠合法
两“重”一“同”
(
)
(
)
(
)
例如:
ED与BA重合,则∠DEF
=∠ABC。
把∠DEF移动,使它的顶点E和∠ABC的顶点B重合,一边EF和BC重合,另一边ED和BA落在BC的同旁。
A
B
C
D
E
F
比较∠ABC
和
∠DEF的大小
例如:
ED落在∠ABC的内部,则∠DEF
<
∠ABC
把∠DEF移动,使它的顶点E和∠ABC的顶点B重合,一边EF和BC重合,另一边ED和BA落在BC的同旁。
A
B
C
D
E
F
(
)
(
)
比较∠ABC
和
∠DEF的大小
D
E
F
D
E
F
D
E
F
A
B
C
A
B
C
A
B
C
∠DEF
>∠ABC
∠DEF
=∠ABC
∠DEF
<
∠ABC
作一个角等于已知角
已知:∠AOB.求作:一个角,使它等于∠AOB.
步骤如下::
(1)作射线O′A′?
(2)以O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D?
(3)以O′为圆心,以OC的长为半径画弧,交O′A′于点C′?
(4)以点C′为圆心,以CD的长为半径画弧,交前弧于点D′?
(5)过D′作射线O′B′
则∠A′O′B′就是所求作的角
O
A
C
B
思考:下图中共有几个角?它们有什么关系?
完成下列问题:
1、图中共有__个角,它们分别是______________
2、∠AOB=____+_____
3、∠AOC=____-_____
4、∠BOC=____-_____
3
∠AOB
∠AOC
∠BOC
∠AOC
∠BOC
∠AOB
∠BOC
∠AOB
∠AOC
按图1填空:
4)∠A0B+∠BOC=
5)∠A0C+∠COD=
6)∠B0D-∠COD=
7)∠A0D-
=∠A0B
O
D
C
B
A
图1
∠AOC
∠AOD
∠BOC
∠BOD
1)
∠D0B
∠BOC
2)
∠C0B
∠AOC
3)
∠D0C+∠COB
∠B0D
>
<
=
同类练习:
A
B
O
C
问题:
已知射线OC是∠AOB的角平分线,你能写出图中各角的关系吗?
OC是∠AOB的二等分线
∠AOC
=∠BOC=1/2
∠AOB
类似地:还有角的三等分线
如图
O
A
B
C
D
⌒
⌒
⌒
1
2
3
OB、OC是∠AOD的三等分线
回到开始的问题,学生张虎和王鹏的对话中说的折扇的大小和长短能判断角的大小吗?
张:我的折扇大一些,所以我的折扇的角也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
结论:角的大小与角的两边张开的大小一致,与所画边的长短无关
34°34’+21°51’=________
180°-52°31’=________
77°42’+34°45’=________
108°-(34°54’+21°33’)=_____
108°18’-56°23’=________
角的加减运算:
4.3.3
余角和补角
认识一个角的余角和补角,并会求一个角的余角和补角;
掌握余角和补角的性质,并能用它解决相关问题.
学习目标
1
2
4
3
O
B
A
M
O
C
D
N
∠1+∠2=90°
∠3+∠4=180°
∠1=300,
∠2=?
∠3=600,
∠4=?
1
2
O
B
A
M
1
B
M
O
1
B
M
O
2
O
A
M
2
O
A
M
∠1+∠2=90°
∠1+∠2=90°
∠AOB=90°
一般地,如果两个角的和等于90°(直角),就说这两个角互为余角.即其中每一个角都是另一个角的余角。
两个角
互为
请你判断:
(1)∠1+∠2=90°则∠1是余角.(
)
(2)
∠1
+∠2+
∠3=90°,则∠1
、∠2、
∠3、互为余角.(
)
×
×
互为余角
∠1、∠2互为余角
∠1是∠2的余角,
或∠2是∠1的余角
一般地,如果两个角的和等于900,就说这两个角互为余角.
互为余角
几何语言表示为:
若∠1+∠2=90°,那么∠1与∠2互为余角
∠1
=
90°—∠2
或:若∠1与∠2互为余角,那么∠1+∠2=90°
找朋友
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
4
3
O
C
D
N
∠3+∠4=180°
∠3+∠4=180°
4
D
N
O
3
O
C
N
4
D
N
O
3
O
C
N
∠DOC=180O
一般地,如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个是另一个角的补角。
两个角
互为
互为补角
若∠1+∠2=180°,则∠1与∠2互为补角
∠1
=
180°—∠2
反过来说也成立:若∠1与∠2互为补角,那么∠1+∠2=180°
几何语言表示为:
找朋友
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
练一练
判断题:
2、互补的两个角不可能相等。(
)
3、钝角没有余角,但一定有补角(
)
?
?
?
1、如果一个角有补角,那么这个角一定是钝角(
)
▲相等的两个角互补,
这两个角是直角;
▲锐角既有余角又有补角;
5、已知∠A=50°,则∠A的余角是____
补角是____
,补角与余角的差是_____.
40
°
130°
90°
6、一个锐角为X度
,它的余角为
______
度
,它的补角为_______
度,则它的补角比余角大___度.
(90-
X)
(180-X)
90
4、
∠A=25°37
,则它的余角
为_______,它的补角为________.
64°23
154°23
填空题:
5)
30°的余角是_____,补角是______。
2)若∠1与∠2互补,则∠1+
∠2=________.
3)
∠1=
180°-
∠2,则∠1与∠2的关系为___________.
180°
互为补角
60°
150°
抢答
反馈练习
1)已知∠1+∠2=90°则
∠1
、∠2互为______.
4)已知∠A=40°,则∠A的余角是
___
补角是___
,补角与余角的差是___.
余角
50°
140°
90°
∠α
∠α
的余角
∠α
的补角
30°
42°
54°
62°23′
看谁答得快
60
°
150
°
48
°
138
°
36
°
126
°
27
°
37
′
117
°
37
′
从上表中你可以得到什么结论?
锐角的补角比它的余角大90度
如图∠1
与∠2互余,∠3
与∠4互余
,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
答:∠2与∠4相等。
∠4=90°-∠3
∴
∠2
=∠4
∵
∠1
与∠2互余,
∵
∠3与∠4互余
,∴
∵
∠1
=∠3,
理由如下:
探究1
等角的余角相等
余角的性质
这里用到了:
等量减等量,差相等
∴
∠2=90°-∠1
,
已知∠1与∠2互补,∠3
与∠4互补。若∠1=∠3,说说∠2和∠4有什么关系?
由∠1与∠2互补,∴
∠2=
180°-
∠1
由∠3与∠4互补,∴
∠4=
180°-
∠3
又因为∠1=∠3,
180°-
∠1=180°-
∠3
所以∠2=∠4
推导性质
1
2
3
4
补角性质
等角的补角相等
画完图后请回答下列问题:
C
O
B
A
D
(1)图中有哪几对互余的角?
(2)你能发现哪几个角是相等的(直角除外)?
(3)你能用一句话概括以上规律吗?
同角的余角相等.
1
2
3
∠1与∠2,∠2与∠3
∠1=∠3
解:
设这个角的度数为x度,
由题意得:
设这个角的度数为x度
请你试一试
1、已知:一个锐角的补角加上
后等于
求:这个角的度数
这个角的三倍
35
x
=
解
得
°
答
:
这
个
角
为
35
例
如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.
仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
O
●
东
南
西
北
●
A
60°
∴射线OA的方向就是南偏东60°,即灯塔A所在的方向.
●
B
●
D
射线OB的方向就是北偏东40°,即客轮B所在的方向.
C
●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向.
射线OD的方向就是南偏西45°,即海岛D所在的方向.
45°
余角、补角的概念:
余角、补角的性质:
(1)
和为90°的两个角称互为余角;(2)
和为180°的两个角称互为补角;
(1)
等角的余角相等;
(2)
等角的补角相等;
今天我们学了什么?
Good
Bye
4.3
角
4.3.1
角
角的两种定义和四种表示方法;
角度制的定义和度量单位之间的相互转换.
学习目标
房顶的角
剪刀的角
圆规的角
楼梯的折角
时针和分针的夹角
棱锥上的角
三角尺上的角
角是由两条具有公共端点的射线组成的图形。
公共端点
顶点
射线
射线
边
边
静态角的概念
角的概念
这个公共端点叫做这个角的顶点.
这两条射线叫做这个角的边.
(
)
(
)
(
)
(
)
(
)
(
)
1.
下面的图形是不是角?
(1)两条直线组成一个角。
(
)
(2)两条射线组成一个角。
(
)
(3)具有公共端点的两条射线组成一个角
。(
)
(4)角的边画得越长,角就越大。
(
)
2.判断下列说法是否正确。
1
2
3
4
5
6
7
8
9
10
11
12
时针和分针的夹角
C
A
B
角也可以看做一条射线绕端点旋转所组成的图形。
动态角的概念
终边
始边
O
A
B
如果一个角的终边旋转到与始边成一条直线时,所成的角叫做平角。
认识平角
B
O
A
(B)
当终边继续旋转,旋转到与始边重合时,所成的角叫做周角。
认识周角
B
在不做特别说明的情况下,我们说的角都指不大于平角的角
角的表示方法
角用“∠”表示,读做“角”。角的表示方法有下面几种:
A
B
C
如:∠ABC
或∠CBA
(1)表示:
(2)
用角的顶点字母表示:
如:∠B
A
B
C
D
这里能用∠
B表示角吗?
(顶点字母写在中间)
(只有一个角时)
角的表示方法
如:∠1、∠2
(3)
用一个数字表示:
A
B
C
D
1
2
A
B
C
D
β
α
如:∠α、∠
β
(4)也可用一个希腊字母表示:
角的表示
角用符号“∠”来表示.
(1)用三个大写字母表示,三个字母应分别写在顶点及两边上的点,顶点的字母必须写在中间.
(2)角也可用一个大写字母表示,这个字母写在顶点处,它只适用于顶点处只有一个角.
∠O
∠AOB
或∠BOA
表示的是同一个角
(3)用一个数字加弧线表示.
1
α
(4)用一个小写希腊字母加弧线表示.
∠1
∠
α
O
A
O
B
试一试
1.把图中的角表示成下列形式:
①∠APO
②∠AOP
③∠OPC,
④∠O
⑤∠COP
⑥∠P。
其中正确的有
(把你认正确的序号都填上。)
P
O
A
C
①
③
⑥
你会了吗?
将图中的角用不同的方法表示出来,并填写下表:
A
D
B
C
E
1
2
α
∠1
∠ACB
∠BAC
∠
β
β
∠ABC
∠BCE
∠α
∠2
∠BAD
∠B
把圆周分成360等分,每一份所对的角叫做
。
记作
“
”
。
把1度的角60等分,每一份所对的角叫做
1
分角。
记作
“
1
′
”
。
把1分的角60等分,每一份所对的角叫做
1
秒角。
记作
“1″
”
。
1度角
1°
以度,分,秒为单位的角的度量制叫做角度制。
角的度量单位:度
、分、秒.
度
分
秒
×60
×60
×3600
÷60
÷3600
÷60
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″
例1
填空
72036/
=
0
解:(1)72036/=720+36/
=720+(36÷60)0
=720+0.60
=72.60
(2)38.170=380+0.17
0
=380+(0.17
×60)/
=380+10/+0.2/
=380+10/+(0.2
×60)//
=380
+10/+12
//
=38010/
12
//
1.用度、分、秒表示:
⑴0.75°= ′= ″
⑵(-)°= ′= ″
⑶16.24°= ° ′ ″
⑷34.37°= ° ′ ″
4
15
45
2700
16
960
16
14
24
34
22
12
练习
小结
1.角的定义一:
有公共端点的两条射线组成的图形
叫做角,这个公共端点叫做角的顶点,这
两条射线叫做角的边。
2.角的定义二:
角可以看成是一条射线绕着它的
端点从一个位置旋转到另一个位置所形成
的图形。射线旋转时经过的平面部分叫角
的内部。
角的表示
角用符号“∠”来表示.
(1)用三个大写字母表示,三个字母应分别写在顶点及两边上的点,顶点的字母必须写在中间.
(2)角也可用一个大写字母表示,这个字母写在顶点处,它只适用于顶点处只有一个角.
∠O
∠AOB
或∠BOA
表示的是同一个角
(3)用一个数字加弧线表示.
1
α
(4)用一个小写希腊字母加弧线表示.
∠1
∠
α
O
A
O
B
5、角的度量单位:度
、分、秒.
度
分
秒
×60
×60
×3600
÷60
÷3600
÷60
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″
4.3.2
角的比较与运算
角的两种比较大小的方法;
会计算角度的和差,能理解两个角的和、差、的意义.
学习目标
问题:有一天学生张虎和王鹏各带了一把折扇(如图),下面是他们的一段对话:
张:我的折扇大一些,所以我的折扇的角
也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
同学们,你们有办法帮他们进行判断吗?
A
B
C
D
E
F
怎样比较∠ABC和∠DEF的大小?
知识回顾:线段的比较方法
1.以“数”
出发,通过度量长度进行数值大
小比较。
度量法
以“数”
出发,通过度量长度,长度大的线段也大。
5
cm
A
B
3
cm
C
D
AB
>
CD
2.从“形”出发,利用线段移动叠合的方法
A
B
A
C
叠合法
叠合
A
(
C
)
A
C
A
B
C
A
A
B
A
B
(AB
>
AC)
(AB
=
AC)
(AB
<
AC)
一,角的比较:
请同学们任意画出两个角比较一下,并讨论你们的比较方法:
B
A
C
E
D
F
你的方法有:
(1)度量法比较
(2)叠合法比较
45°
60°
A
o
B
D
E
F
度量法
所以:∠AOB<∠DEF
读数为45
读数为60
ED落在∠ABC的外部,则∠DEF
>
∠ABC。
把∠DEF移动,使它的顶点E和∠ABC的顶点B重合,一边EF和BC重合,另一边ED和BA落在BC的同旁。
A
B
C
D
E
F
(
)
(
)
比较∠ABC
和
∠DEF的大小
叠合法
两“重”一“同”
(
)
(
)
(
)
例如:
ED与BA重合,则∠DEF
=∠ABC。
把∠DEF移动,使它的顶点E和∠ABC的顶点B重合,一边EF和BC重合,另一边ED和BA落在BC的同旁。
A
B
C
D
E
F
比较∠ABC
和
∠DEF的大小
例如:
ED落在∠ABC的内部,则∠DEF
<
∠ABC
把∠DEF移动,使它的顶点E和∠ABC的顶点B重合,一边EF和BC重合,另一边ED和BA落在BC的同旁。
A
B
C
D
E
F
(
)
(
)
比较∠ABC
和
∠DEF的大小
D
E
F
D
E
F
D
E
F
A
B
C
A
B
C
A
B
C
∠DEF
>∠ABC
∠DEF
=∠ABC
∠DEF
<
∠ABC
作一个角等于已知角
已知:∠AOB.求作:一个角,使它等于∠AOB.
步骤如下::
(1)作射线O′A′?
(2)以O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D?
(3)以O′为圆心,以OC的长为半径画弧,交O′A′于点C′?
(4)以点C′为圆心,以CD的长为半径画弧,交前弧于点D′?
(5)过D′作射线O′B′
则∠A′O′B′就是所求作的角
O
A
C
B
思考:下图中共有几个角?它们有什么关系?
完成下列问题:
1、图中共有__个角,它们分别是______________
2、∠AOB=____+_____
3、∠AOC=____-_____
4、∠BOC=____-_____
3
∠AOB
∠AOC
∠BOC
∠AOC
∠BOC
∠AOB
∠BOC
∠AOB
∠AOC
按图1填空:
4)∠A0B+∠BOC=
5)∠A0C+∠COD=
6)∠B0D-∠COD=
7)∠A0D-
=∠A0B
O
D
C
B
A
图1
∠AOC
∠AOD
∠BOC
∠BOD
1)
∠D0B
∠BOC
2)
∠C0B
∠AOC
3)
∠D0C+∠COB
∠B0D
>
<
=
同类练习:
A
B
O
C
问题:
已知射线OC是∠AOB的角平分线,你能写出图中各角的关系吗?
OC是∠AOB的二等分线
∠AOC
=∠BOC=1/2
∠AOB
类似地:还有角的三等分线
如图
O
A
B
C
D
⌒
⌒
⌒
1
2
3
OB、OC是∠AOD的三等分线
回到开始的问题,学生张虎和王鹏的对话中说的折扇的大小和长短能判断角的大小吗?
张:我的折扇大一些,所以我的折扇的角也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
结论:角的大小与角的两边张开的大小一致,与所画边的长短无关
34°34’+21°51’=________
180°-52°31’=________
77°42’+34°45’=________
108°-(34°54’+21°33’)=_____
108°18’-56°23’=________
角的加减运算:
4.3.3
余角和补角
认识一个角的余角和补角,并会求一个角的余角和补角;
掌握余角和补角的性质,并能用它解决相关问题.
学习目标
1
2
4
3
O
B
A
M
O
C
D
N
∠1+∠2=90°
∠3+∠4=180°
∠1=300,
∠2=?
∠3=600,
∠4=?
1
2
O
B
A
M
1
B
M
O
1
B
M
O
2
O
A
M
2
O
A
M
∠1+∠2=90°
∠1+∠2=90°
∠AOB=90°
一般地,如果两个角的和等于90°(直角),就说这两个角互为余角.即其中每一个角都是另一个角的余角。
两个角
互为
请你判断:
(1)∠1+∠2=90°则∠1是余角.(
)
(2)
∠1
+∠2+
∠3=90°,则∠1
、∠2、
∠3、互为余角.(
)
×
×
互为余角
∠1、∠2互为余角
∠1是∠2的余角,
或∠2是∠1的余角
一般地,如果两个角的和等于900,就说这两个角互为余角.
互为余角
几何语言表示为:
若∠1+∠2=90°,那么∠1与∠2互为余角
∠1
=
90°—∠2
或:若∠1与∠2互为余角,那么∠1+∠2=90°
找朋友
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
4
3
O
C
D
N
∠3+∠4=180°
∠3+∠4=180°
4
D
N
O
3
O
C
N
4
D
N
O
3
O
C
N
∠DOC=180O
一般地,如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个是另一个角的补角。
两个角
互为
互为补角
若∠1+∠2=180°,则∠1与∠2互为补角
∠1
=
180°—∠2
反过来说也成立:若∠1与∠2互为补角,那么∠1+∠2=180°
几何语言表示为:
找朋友
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
练一练
判断题:
2、互补的两个角不可能相等。(
)
3、钝角没有余角,但一定有补角(
)
?
?
?
1、如果一个角有补角,那么这个角一定是钝角(
)
▲相等的两个角互补,
这两个角是直角;
▲锐角既有余角又有补角;
5、已知∠A=50°,则∠A的余角是____
补角是____
,补角与余角的差是_____.
40
°
130°
90°
6、一个锐角为X度
,它的余角为
______
度
,它的补角为_______
度,则它的补角比余角大___度.
(90-
X)
(180-X)
90
4、
∠A=25°37
,则它的余角
为_______,它的补角为________.
64°23
154°23
填空题:
5)
30°的余角是_____,补角是______。
2)若∠1与∠2互补,则∠1+
∠2=________.
3)
∠1=
180°-
∠2,则∠1与∠2的关系为___________.
180°
互为补角
60°
150°
抢答
反馈练习
1)已知∠1+∠2=90°则
∠1
、∠2互为______.
4)已知∠A=40°,则∠A的余角是
___
补角是___
,补角与余角的差是___.
余角
50°
140°
90°
∠α
∠α
的余角
∠α
的补角
30°
42°
54°
62°23′
看谁答得快
60
°
150
°
48
°
138
°
36
°
126
°
27
°
37
′
117
°
37
′
从上表中你可以得到什么结论?
锐角的补角比它的余角大90度
如图∠1
与∠2互余,∠3
与∠4互余
,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
答:∠2与∠4相等。
∠4=90°-∠3
∴
∠2
=∠4
∵
∠1
与∠2互余,
∵
∠3与∠4互余
,∴
∵
∠1
=∠3,
理由如下:
探究1
等角的余角相等
余角的性质
这里用到了:
等量减等量,差相等
∴
∠2=90°-∠1
,
已知∠1与∠2互补,∠3
与∠4互补。若∠1=∠3,说说∠2和∠4有什么关系?
由∠1与∠2互补,∴
∠2=
180°-
∠1
由∠3与∠4互补,∴
∠4=
180°-
∠3
又因为∠1=∠3,
180°-
∠1=180°-
∠3
所以∠2=∠4
推导性质
1
2
3
4
补角性质
等角的补角相等
画完图后请回答下列问题:
C
O
B
A
D
(1)图中有哪几对互余的角?
(2)你能发现哪几个角是相等的(直角除外)?
(3)你能用一句话概括以上规律吗?
同角的余角相等.
1
2
3
∠1与∠2,∠2与∠3
∠1=∠3
解:
设这个角的度数为x度,
由题意得:
设这个角的度数为x度
请你试一试
1、已知:一个锐角的补角加上
后等于
求:这个角的度数
这个角的三倍
35
x
=
解
得
°
答
:
这
个
角
为
35
例
如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.
仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
O
●
东
南
西
北
●
A
60°
∴射线OA的方向就是南偏东60°,即灯塔A所在的方向.
●
B
●
D
射线OB的方向就是北偏东40°,即客轮B所在的方向.
C
●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向.
射线OD的方向就是南偏西45°,即海岛D所在的方向.
45°
余角、补角的概念:
余角、补角的性质:
(1)
和为90°的两个角称互为余角;(2)
和为180°的两个角称互为补角;
(1)
等角的余角相等;
(2)
等角的补角相等;
今天我们学了什么?
Good
Bye
