苏科版八年级上册数学上册 6.1函数学案(含答案)
文档属性
| 名称 | 苏科版八年级上册数学上册 6.1函数学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 262.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览



文档简介
一次函数章节----函数教案(含答案)
知识梳理:
概念:
1.变量:在一个变化过程中可以取不同数值的量。
2.常量:在一个变化过程中只能取同一数值的量。
3.函数:一般的,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就把x称为自变量,把y称为因变量,y是x的函数。
4.表示方法:图像法、解析式法、列表法。
5.注意点:一个变量的数值随另一个变量的数值的变化而发生变化。x与y是单值对应。
例题讲解:
例1.函数中,自变量的取值范围是(
)
A.
B.
C.
D.
例2
.下列函数中,自变量的取值范围是≥3的是(
)
(A)
(B)
(C)
(D)
例3
.函数的自变量的取值范围是(
)
A.
B.
C.
D.
例4
.函数y=+中自变量x的取值范围是
A.x≤2
B.x=3
C.
x<2且x≠3
D.x≤2且x≠3
例5
.函数中自变量的取值范围是()
A.
B.
C.
D.
例6
.一定质量的二氧化碳,当它的体积V=5,密度p=1.98kg/时,p与V
之间的函数关系式是(
)
A.p=9.9V
B.
C.
D.
例7
.下列函数中,自变量的取值范围选取错误的是
A.y=2x2中,x取全体实数
B.y=中,x取x≠-1的实数
C.y=中,x取x≥2的实数
D.y=中,x取x≥-3的实数
例8
.要画一个面积为20cm2的长方形,其长为xcm,宽为ycm,在这一变化过程中,常量与变量分别为(
)
A.常量为20,变量为x,y;
B.常量为20、y,变量为x;
C.常量为20、x,变量为y;
D.常量为x、y,变量为20;
例9
.如图,分别给出了变量y与x之间的对应关系,y不是x的函数的是(
)
例10.进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价.若设平均每次降价的百分率是x,降价后的价格为y元,原价为a元,则y与x之间的函数关系式为(
)
A.y=2a(x-1)
B.y=2a(1-x)
C.y=a(1-x2)
D.y=a(1-x)2
例11.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,
按时赶到了学校.
图2描述了他上学的情景,下列说法中错误的是
A.修车时间为15分钟
B.学校离家的距离为2000米
C.到达学校时共用时间20分钟
D.自行车发生故障时离家距离为1000米
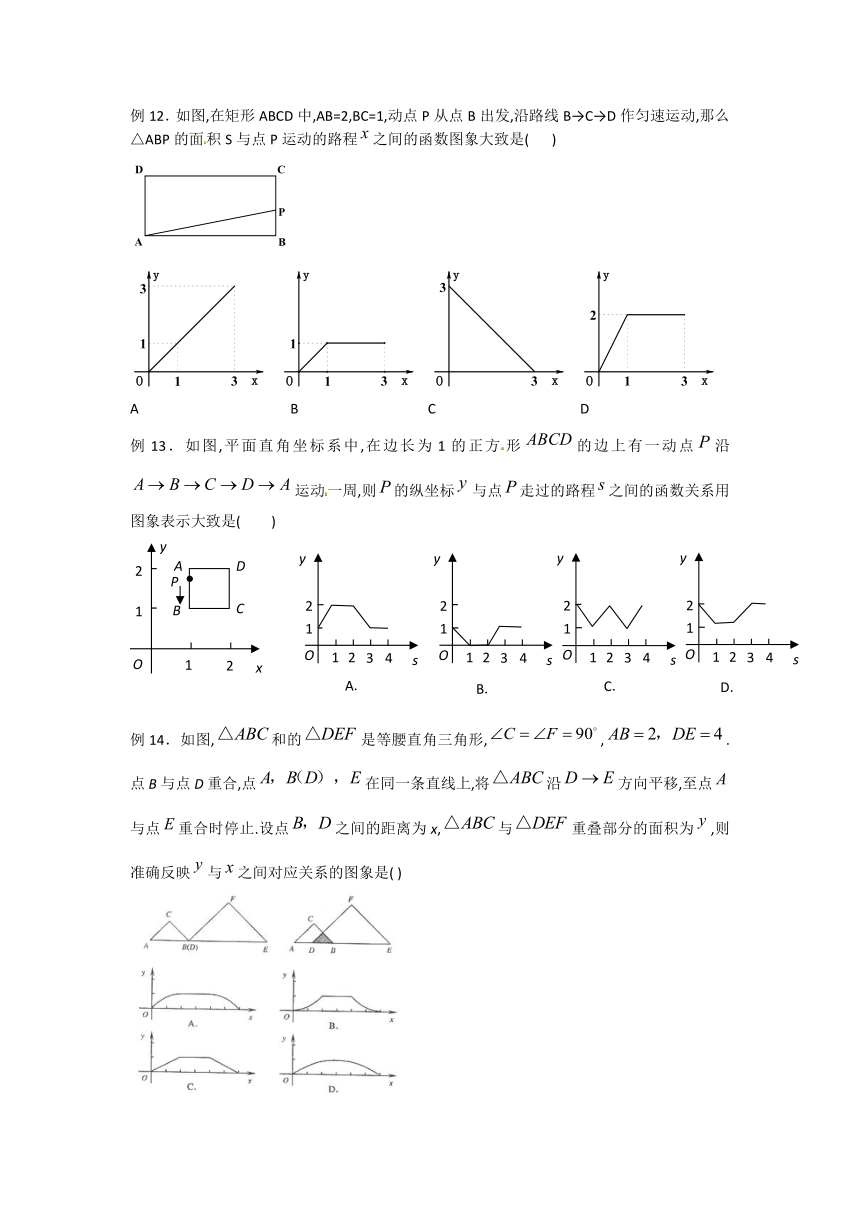
例12.如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积S与点P运动的路程之间的函数图象大致是(
)
A
B
C
D
例13.如图,平面直角坐标系中,在边长为1的正方形的边上有一动点沿运动一周,则的纵坐标与点走过的路程之间的函数关系用图象表示大致是(
)
例14.如图,和的是等腰直角三角形,,.点B与点D重合,点在同一条直线上,将沿方向平移,至点与点重合时停止.设点之间的距离为x,与重叠部分的面积为,则准确反映与之间对应关系的图象是(
)
例15.如图,边长为1和2的两个正方形的一边在同一水平线上,小正方形沿水平线自左向右匀速穿过大正方形,下图反映了这个运动的全过程.设小正方形的运动时间为t,两正方形重叠部分面积为S,则S与t的函数图象大致为(
).
例16.如图5,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动连结DP,过点A作AE⊥DP,垂足为E,设DP=,AE=,
则能反映与之间函数关系的大致图象是(
)
例17.已知函数,当=1时,的值是________
例18.在函数y=中,自变量x的取值范围是____________________
.
例19.已知函数,则__________.
例20.矩形面积为,长为,那么这个矩形的宽与长的函数关系为______.
例21.矩形的面积为2,一条边的长为x,另一条边的长为y,则用x表示y的函数解析式为__________________________(其中x>0)
例22.某同学带10元钱去新华书店买数学辅导书,已知每册定价1元8角,设买书后余下的钱数y(元)和买书的册数x
,则y与x的函数关系为__________________.其中自变量x的取值范围为__________________________.
例23.国家为了关心广大农民群众,增强农民抵御大病风险的能力,积极推行农村医疗保险制度.某市根据本地的实际情况,制定了纳入医疗保险的农民医疗费用报销规定,享受医保的农民可在定点医院就医,在规定的药品品种范围内用药,由患者先垫付医疗费用,年终到医保中心报销.医疗费的报销比例标准如下表:
费用范围
500元以下(含500元)
超过500元且不超过10000元的部分
超过10000元的部分
报销
比例标准
不予报销
70%
80%
(1)设某农民一年的实际医疗费为x元(500(2)若某农民一年内自付医疗费为2600元(自付医疗费=实际医疗费-按标准报销的金额),则该农民当年实际医疗费为多少元?
(3)若某农民一年内自付医疗费不少于4100元,则该农民当年实际医疗费至少为多少元?
例题答案:
1
.B
2
.D
3
.C
4
.A
5
.C
6
.B
7
.D
8
.A
9
.B
10.D
11.A
12.B
13.D
14.B
15.C
16.C
17.2
18.x≠-2
19.1
20.
21.Y=
22.y=10-1.8x
,
0≤x≤5的整数
23.解:(1)y=
(x-500)
(500;
(2)
x=7500(元);
(3)
x≥13750.
巩固练习:
1.三角形一边的长为30
cm,这边上的高为h
cm,面积为S
cm2,则S与h的关系为_______,
其中常量是_______,变量是_______,自变量是_______,因变量是_______.
2.下列各式:①y=x2+3;②y2=x+3;③.其中,x是自变量,y是x的函数的是_______
(填序号).
3.李大爷出去散步,从家出发走了20
min,来到一个离家900
m远的阅报亭,看了10
min报纸后,用了20
min回家.下列图形中表示李大爷离家距离与时间之间的关系是
(
)
4.写出下列函数的关系式,并求出自变量的取值范围.
(1)矩形的周长为12,求它的面积S与一边的长x之间的关系式.
(2)梯形的下底长为10
cm,上底与高都是x
cm,求梯形的面积S(cm2)与高x(cm)之间的关系式.
(3)行走距离为100
km,求平均速度v(km/h)与所走时间t(h)的关系式.
(4)某种储蓄月利率为0.15%,存入10
000元本金,求本金与利息的和y(元)与所存月数x之间的关系式.
5.在圆周长公式C=2r中,变量是
(
)
A.C、2、、r
B.C、、r
C.C、r
D.r
6.函数中,自变量x的取值范围是
(
)
A.x≠0
B.x≠1
C.x≠一1
D.x=l
7.下列关于变量x、y的关系式:①3x一2y=5;②y=|x|;③2x一y2=10.其中表示y是x的函数关系的是
(
)
A.①②③
B.①②
C.②③
D.①③
8.从高楼楼顶掉下一物体,物体下落的距离s与下落的时间t有的关系,根据公式填写下表:
下落时间t/s
1
2
3
4
···
下落距离s/m
···
可知__________是自变量,_________是___________的函数.
9.当x=________时,函数y=一5x+l的函数值为0;已知函数,当y=l时,x=______.
10.直角三角形的面积为60
cm2,两直角边长分别为xcm、ycm.
(1)当x=10
cm时,y的值是多少?
(2)当y=8
cm时,x的值是多少?
(3)y是x的函数吗?如果是,请写出表示它们关系的式子.
x/kg
0
1
2
3
4
y/cm
12
12.5
13
13.5
14
11.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)有下面的关系.
根据上述关系回答:
(1)弹簧不挂物体时的长度是_____________.
(2)所挂物体的质量为1
kg时弹簧伸长______________.
(3)挂6
kg的物体时弹簧的长度(在弹性限度内)是____________.
(4)下列各式:①y+x=2;②x=y一12;③y=12+0.5x;④x=12+0.5y,其中表示弹簧总长y(cm)与所挂物体质量x(kg)的关系式是__________(填序号).
(5)上式中,有_________个变量,________是自变量,__________是因变量.
12.
汽车的速度随时间变化的情况如图所示.
(1)这辆汽车的最高时速是多少?
(2)汽车在行驶了多长时间后停了下来,停了多长时间?
(3)汽车在第一次匀速行驶时共用了几分钟?速度是多少?在这段时间内,它行驶了多远?
巩固练习答案
1.S=
15h
15
h
、S
h
S
2.①③
3.D
4.(1)S=x(6一x),x的取值范围为0(2)S=(x+10)x,x的取值范围为0(3)V=100/t的取值范围为t>0
(4)y=10
000(1+0.15%x),x的取值范围为x为正整数
5.C
6.B
7.B
8.填表略.t
s
t
9.
1
10.(1)12
(2)15
(3)是
11.(1)12
cm
(2)0.5
cm
(3)15
cm
(4)③
(5)两
x
y
12.(1)120千米/时
(2)10分钟
2分钟
(3)4分钟
90千米/时
6千米
知识梳理:
概念:
1.变量:在一个变化过程中可以取不同数值的量。
2.常量:在一个变化过程中只能取同一数值的量。
3.函数:一般的,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就把x称为自变量,把y称为因变量,y是x的函数。
4.表示方法:图像法、解析式法、列表法。
5.注意点:一个变量的数值随另一个变量的数值的变化而发生变化。x与y是单值对应。
例题讲解:
例1.函数中,自变量的取值范围是(
)
A.
B.
C.
D.
例2
.下列函数中,自变量的取值范围是≥3的是(
)
(A)
(B)
(C)
(D)
例3
.函数的自变量的取值范围是(
)
A.
B.
C.
D.
例4
.函数y=+中自变量x的取值范围是
A.x≤2
B.x=3
C.
x<2且x≠3
D.x≤2且x≠3
例5
.函数中自变量的取值范围是()
A.
B.
C.
D.
例6
.一定质量的二氧化碳,当它的体积V=5,密度p=1.98kg/时,p与V
之间的函数关系式是(
)
A.p=9.9V
B.
C.
D.
例7
.下列函数中,自变量的取值范围选取错误的是
A.y=2x2中,x取全体实数
B.y=中,x取x≠-1的实数
C.y=中,x取x≥2的实数
D.y=中,x取x≥-3的实数
例8
.要画一个面积为20cm2的长方形,其长为xcm,宽为ycm,在这一变化过程中,常量与变量分别为(
)
A.常量为20,变量为x,y;
B.常量为20、y,变量为x;
C.常量为20、x,变量为y;
D.常量为x、y,变量为20;
例9
.如图,分别给出了变量y与x之间的对应关系,y不是x的函数的是(
)
例10.进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价.若设平均每次降价的百分率是x,降价后的价格为y元,原价为a元,则y与x之间的函数关系式为(
)
A.y=2a(x-1)
B.y=2a(1-x)
C.y=a(1-x2)
D.y=a(1-x)2
例11.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,
按时赶到了学校.
图2描述了他上学的情景,下列说法中错误的是
A.修车时间为15分钟
B.学校离家的距离为2000米
C.到达学校时共用时间20分钟
D.自行车发生故障时离家距离为1000米
例12.如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积S与点P运动的路程之间的函数图象大致是(
)
A
B
C
D
例13.如图,平面直角坐标系中,在边长为1的正方形的边上有一动点沿运动一周,则的纵坐标与点走过的路程之间的函数关系用图象表示大致是(
)
例14.如图,和的是等腰直角三角形,,.点B与点D重合,点在同一条直线上,将沿方向平移,至点与点重合时停止.设点之间的距离为x,与重叠部分的面积为,则准确反映与之间对应关系的图象是(
)
例15.如图,边长为1和2的两个正方形的一边在同一水平线上,小正方形沿水平线自左向右匀速穿过大正方形,下图反映了这个运动的全过程.设小正方形的运动时间为t,两正方形重叠部分面积为S,则S与t的函数图象大致为(
).
例16.如图5,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动连结DP,过点A作AE⊥DP,垂足为E,设DP=,AE=,
则能反映与之间函数关系的大致图象是(
)
例17.已知函数,当=1时,的值是________
例18.在函数y=中,自变量x的取值范围是____________________
.
例19.已知函数,则__________.
例20.矩形面积为,长为,那么这个矩形的宽与长的函数关系为______.
例21.矩形的面积为2,一条边的长为x,另一条边的长为y,则用x表示y的函数解析式为__________________________(其中x>0)
例22.某同学带10元钱去新华书店买数学辅导书,已知每册定价1元8角,设买书后余下的钱数y(元)和买书的册数x
,则y与x的函数关系为__________________.其中自变量x的取值范围为__________________________.
例23.国家为了关心广大农民群众,增强农民抵御大病风险的能力,积极推行农村医疗保险制度.某市根据本地的实际情况,制定了纳入医疗保险的农民医疗费用报销规定,享受医保的农民可在定点医院就医,在规定的药品品种范围内用药,由患者先垫付医疗费用,年终到医保中心报销.医疗费的报销比例标准如下表:
费用范围
500元以下(含500元)
超过500元且不超过10000元的部分
超过10000元的部分
报销
比例标准
不予报销
70%
80%
(1)设某农民一年的实际医疗费为x元(500
(3)若某农民一年内自付医疗费不少于4100元,则该农民当年实际医疗费至少为多少元?
例题答案:
1
.B
2
.D
3
.C
4
.A
5
.C
6
.B
7
.D
8
.A
9
.B
10.D
11.A
12.B
13.D
14.B
15.C
16.C
17.2
18.x≠-2
19.1
20.
21.Y=
22.y=10-1.8x
,
0≤x≤5的整数
23.解:(1)y=
(x-500)
(500
(2)
x=7500(元);
(3)
x≥13750.
巩固练习:
1.三角形一边的长为30
cm,这边上的高为h
cm,面积为S
cm2,则S与h的关系为_______,
其中常量是_______,变量是_______,自变量是_______,因变量是_______.
2.下列各式:①y=x2+3;②y2=x+3;③.其中,x是自变量,y是x的函数的是_______
(填序号).
3.李大爷出去散步,从家出发走了20
min,来到一个离家900
m远的阅报亭,看了10
min报纸后,用了20
min回家.下列图形中表示李大爷离家距离与时间之间的关系是
(
)
4.写出下列函数的关系式,并求出自变量的取值范围.
(1)矩形的周长为12,求它的面积S与一边的长x之间的关系式.
(2)梯形的下底长为10
cm,上底与高都是x
cm,求梯形的面积S(cm2)与高x(cm)之间的关系式.
(3)行走距离为100
km,求平均速度v(km/h)与所走时间t(h)的关系式.
(4)某种储蓄月利率为0.15%,存入10
000元本金,求本金与利息的和y(元)与所存月数x之间的关系式.
5.在圆周长公式C=2r中,变量是
(
)
A.C、2、、r
B.C、、r
C.C、r
D.r
6.函数中,自变量x的取值范围是
(
)
A.x≠0
B.x≠1
C.x≠一1
D.x=l
7.下列关于变量x、y的关系式:①3x一2y=5;②y=|x|;③2x一y2=10.其中表示y是x的函数关系的是
(
)
A.①②③
B.①②
C.②③
D.①③
8.从高楼楼顶掉下一物体,物体下落的距离s与下落的时间t有的关系,根据公式填写下表:
下落时间t/s
1
2
3
4
···
下落距离s/m
···
可知__________是自变量,_________是___________的函数.
9.当x=________时,函数y=一5x+l的函数值为0;已知函数,当y=l时,x=______.
10.直角三角形的面积为60
cm2,两直角边长分别为xcm、ycm.
(1)当x=10
cm时,y的值是多少?
(2)当y=8
cm时,x的值是多少?
(3)y是x的函数吗?如果是,请写出表示它们关系的式子.
x/kg
0
1
2
3
4
y/cm
12
12.5
13
13.5
14
11.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)有下面的关系.
根据上述关系回答:
(1)弹簧不挂物体时的长度是_____________.
(2)所挂物体的质量为1
kg时弹簧伸长______________.
(3)挂6
kg的物体时弹簧的长度(在弹性限度内)是____________.
(4)下列各式:①y+x=2;②x=y一12;③y=12+0.5x;④x=12+0.5y,其中表示弹簧总长y(cm)与所挂物体质量x(kg)的关系式是__________(填序号).
(5)上式中,有_________个变量,________是自变量,__________是因变量.
12.
汽车的速度随时间变化的情况如图所示.
(1)这辆汽车的最高时速是多少?
(2)汽车在行驶了多长时间后停了下来,停了多长时间?
(3)汽车在第一次匀速行驶时共用了几分钟?速度是多少?在这段时间内,它行驶了多远?
巩固练习答案
1.S=
15h
15
h
、S
h
S
2.①③
3.D
4.(1)S=x(6一x),x的取值范围为0
(4)y=10
000(1+0.15%x),x的取值范围为x为正整数
5.C
6.B
7.B
8.填表略.t
s
t
9.
1
10.(1)12
(2)15
(3)是
11.(1)12
cm
(2)0.5
cm
(3)15
cm
(4)③
(5)两
x
y
12.(1)120千米/时
(2)10分钟
2分钟
(3)4分钟
90千米/时
6千米
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
