一次函数的图象（2）

(共31张PPT)
复习：
1.一次函数y = kx + b的图象是什么图形？你是通过确定几个点来作一次函数y=kx+b的图象的呢？
2.求作函数
的图象。
y=kx+b的图象是一条直线；
两个点。
y
x
（1）正比例函数y=kx的图象有什么特点？
(2)你作正比例函数y=kx的图象时描了几个点
想
一
想
0
2
1
-1
-1
2
1
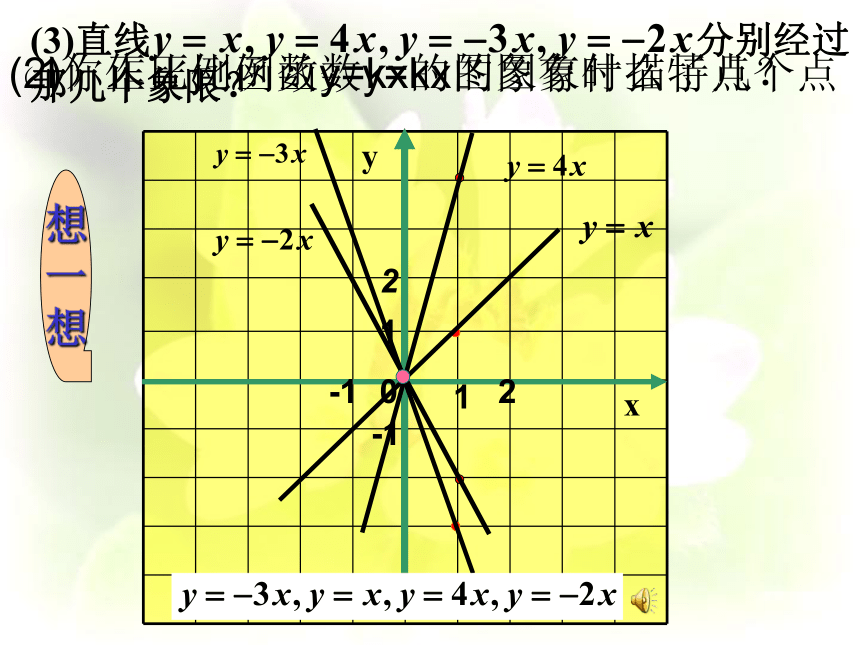
(3)直线 分别经过
那几个象限？
归纳总结：
一、正比例函数y = kx (k≠0)图象的性质
1、正比例函数 y = kx 的图象都是经过坐标原点（0，0）的一条直线；
2、(1)当 k＞0时，y=kx经过一、三象限，
(2)当 k＜0时，y=kx经过二、四象限；
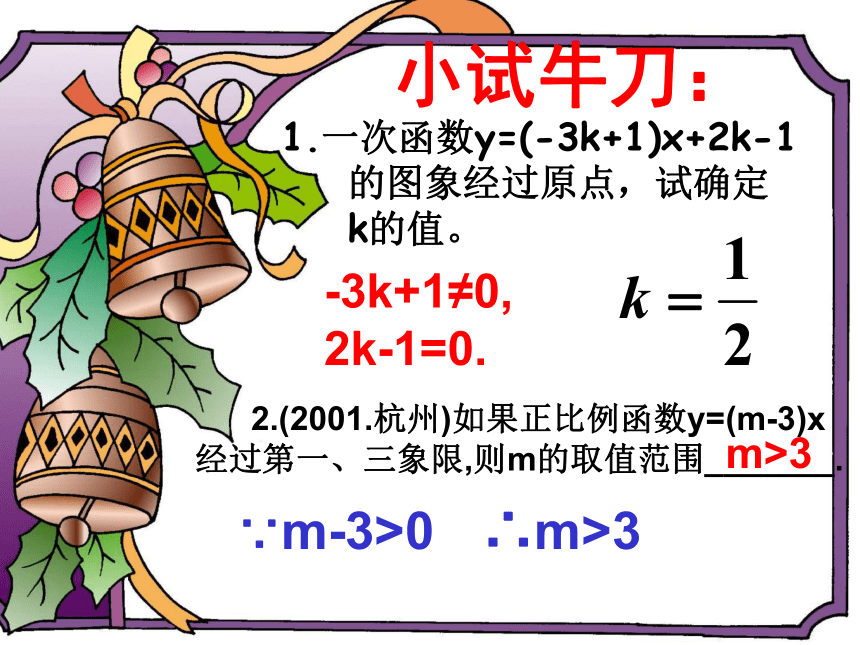
1.一次函数y=(-3k+1)x+2k-1
的图象经过原点，试确定
k的值。
2.(2001.杭州)如果正比例函数y=(m-3)x经过第一、三象限,则m的取值范围_______.
小试牛刀：
-3k+1≠0,
2k-1=0.
∵m-3>0
∴m>3
m>3
探索发现
对一次函数y=x+4，x依次取-3,-2,-1,0,1,2,3
逐渐增大的过程中，y的值是否也在增大？
对y=-x+4呢？
x … -3 -2 -1 0 1 2 3 …
y=x+4 … …
y=-x+4 … …
1
2
3
4 5 6 7
7
6
5
4 3 2 1
y增大
y减小
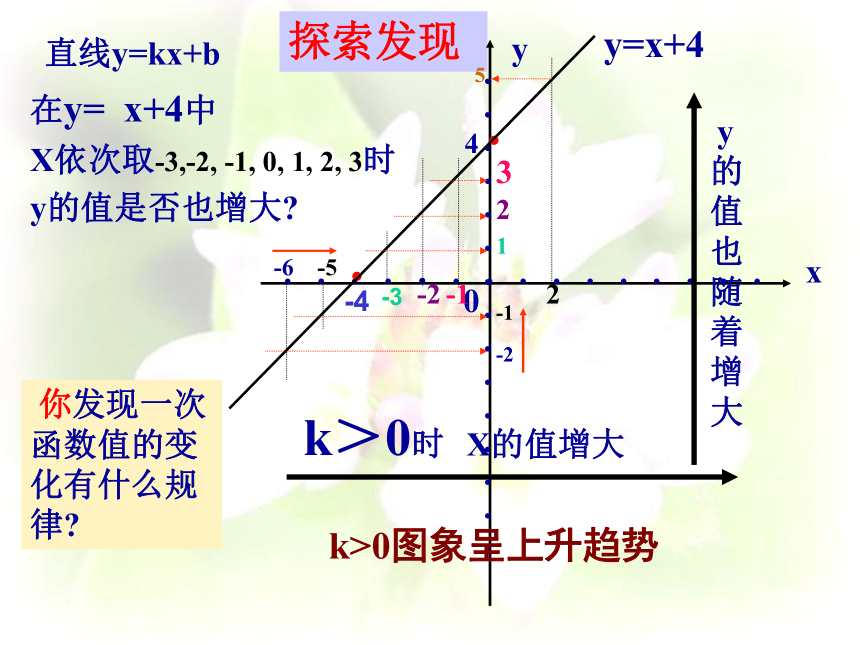
直线y=kx+b
在y= x+4中
X依次取-3,-2, -1, 0, 1, 2, 3时
y的值是否也增大
探索发现
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
0
y
x
·
·
y=x+4
-6
-5
-2
-1
2
-2
-1
1
2
3
5
的值也随着增大
y
X的值增大
k＞0时
你发现一次函数值的变化有什么规律
4
k>0图象呈上升趋势
-4
-3
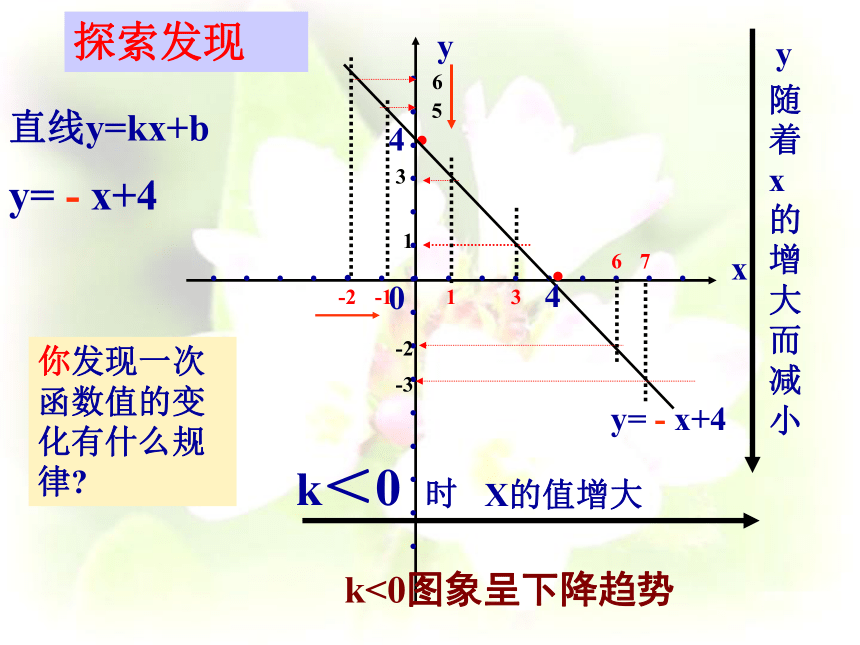
直线y=kx+b
y= - x+4
探索发现
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
0
y
x
·
·
y= - x+4
X的值增大
k＜0 时
y
随着 x 的 增 大而减小
6
5
3
1
-2
-3
-2
1
-1
3
6
7
你发现一次函数值的变化有什么规律
4
k<0图象呈下降趋势
4
归纳总结：
一次函数
y = kx + b
（k≠0）
的性质
在一次函数y = kx+b中
当k>0时，y的值随着x值的增大而增大，
当k<0时，y的值随着x值的增大而减小，
图象呈上升趋势；
图象呈下降趋势。
下列函数,y的值随着x值的增大如何变化？
增大
减小
增大
减小
2、写出m的3个值，使相应的
一次函数y=(2m-1)x+2的值都
是随着x值的增大而减小.
2m-1<0
x … -3 -2 -1 0 1 2 3 …
y=2x … …
y=2x+2 … …
-6 -4 -2 0 2 4 6
-6+2
-4+2
-2+2
0+2
2+2
4+2
6+2
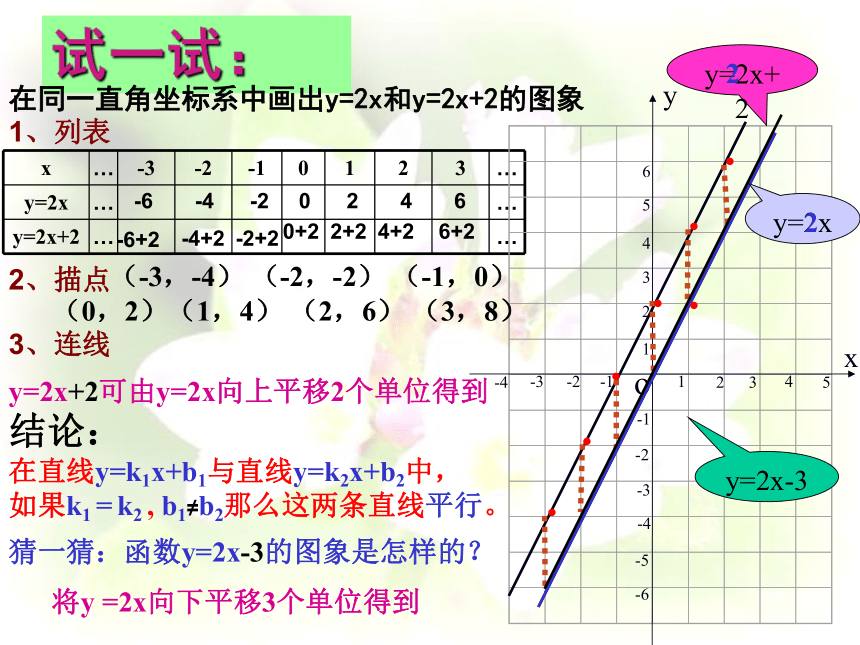
试一试：
在同一直角坐标系中画出y=2x和y=2x+2的图象
1、列表
y






























































































































o
1
2
3
4
5
-1
-2
-3
-4
-5
-6
2
1
3
4
5
6
-1
-2
-3
-4
x
·
·
·
·
·
·
2、描点
3、连线
y=2x-3
（-3，-4） （-2，-2） （-1，0）
（0，2）（1，4） （2，6） （3，8）
猜一猜：函数y=2x-3的图象是怎样的？
y=2x
y=2x+2
结论：
在直线y=k1x+b1与直线y=k2x+b2中，
如果k1 = k2 , b1≠b2那么这两条直线平行。
2
2
·
y=2x+2可由y=2x向上平移2个单位得到
将y =2x向下平移3个单位得到
想一想：
在同一坐标系中画出y=2x，y=2x+2和y=2x-3的图象
y






























































































































o
1
2
3
4
5
-1
-2
-3
-4
-5
-6
2
1
3
4
5
6
-1
-2
-3
-4
x
y=2x-3
那么：函数y=2x+b的图象是怎样得到的？
y=2x
y=2x+2
y=kx+b可由y=kx向上或者向下平移得到。
·
y=2x+2可由y=2x向上平移2个单位得到
y=2x-3可由y =2x向下平移3个单位得到
函数y=kx+b能由y=kx得到吗？
b>0,向上平移；b<0，向下平移。
y=2x经过那些象限？
y=2x+2呢？
y=2x-3呢？
当k>0时，y=kx+b呢？
一、二、三
一、三、四
一、三
归纳总结：
二、一次函数
y = kx + b
（k≠0）
经过象限：
k>0
b>0
b<0
一、三、
一、三、
k<0
b>0
b<0
二、四、
二、四、
x
y
o
y = - 2x - 3
y = -2x + 1
y = 2x + 1
y=2x-2
y=-2x
y=2x
k<0
k>0
二
四
一
三
y
x
0
D
y
x
0
A
y
x
0
C
y
x
0
B
练习1 已知函数 y = kx的图象在二、四象限，那么函数y = kx-k的图象可能是（ ）
B
练习2 1）若直线 y =mx+n经过第一、 二、三象限，讨论m、n的符号。
m＞0，n＞0
练习2 2）已知一次函数 y=(1-2m)x+m-1 ,
求满足下列条件的m的值：
（1）函数值y 随x的增大而增大；
（2）函数图象与y 轴的负半轴相交；
（3）函数的图象过第二、三、四象限；
（4）函数的图象过原点。
　练习3一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是（　 　）
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
A
4、一次函数y=kx+b的图象如图所示，则
k 0,b 0
x
y
o
<
<
1、y=|x|中，x y的函数，y x 的函数（填“是”或“不是”），图象为
不是
是
2、某企业去年积压产品a件(a>0)，今年预计每月销售产
品2b件，同时每月可生产出产品b个，若产品积压量y(件)
是今年开工时间（月）的函数，则它的图象只能是（ ）
3、拖拉机开始工作时，油箱中有油24L，可用6小时。那么油箱中剩余原油量y（L）与工作时间x（h）之间的函数关系式和图象是( )
A. y=4x-24（0≤x ≤ 6） B. y=24-4x
C. y=24-4x (0≤x ≤ 6 ) D. y=-24+4x
x/ 吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
例3. 如图，l1反映了某公司产品的销售收入与销售量的关系，
l1
l2
（1）当销售量为2吨时，销售收入＝　　　　元，
　　　销售成本＝　　　　元；
2000
3000
　　　　l2反映了该公司产品的销售成本与销售量的关系，根据图意填空：
x/ 吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
（2）当销售量为6吨时，销售收入＝　　　　元，
　　　销售成本＝　　　　元；
6000
5000
（3）当销售量为　　时，销售收入等于销售成本；
4吨
x/ 吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
（4）当销售量　　　　时，该公司赢利（收入大于成本）；
　　当销售量　　　　时，该公司亏损（收入小于成本）；
大于4吨
小于4吨
8.已知点(-1,a)和(1/2,b)都在直线
上,试比较a和b的大小.
9.若一次函数y=kx+b的图象经过点
（ x1,y1）和（x2,y2)，且k>0，
则当x1因为k >0,所以y随x的增大而增大
<
解：∵k=2/3>0,
∴y随x的增大而增大
又 ∵-1<1/2
∴ a10.已知一次函数
(1)a为何值时, 函数图象经过原点；
(2)a为何值时，函数图象平行于直线y=-x;
(3)a为何值时， y随x的增大而减小。
解：一次函数y=kx+b,必须满足k≠0，即3-a≠0
因而a≠3.
(1)若图象经过原点，则b=0,即
所以 , a=±3;
而a≠3,所以 a=-3.
(2)若图象平行于y=-x，则3-a=-1,所以 a=4.
(3)若y随x的增大而减小，则3-a<0,所以a>3.
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
0
y
x
·
1
·
-2
如直线y=(1-3k)x+2k-1与y轴
交于B点(0,-2), 则k的值是多
少
A(3/4,0)
B(0,-2)
如直线y=(1-3k)x+2k-1与x轴
交于A点(3/4,0), 则k的值是多少
∵0=(1-3k)(3/4)+2k-1
∴k= -1
∵-2=(1-3k)(0)+2k-1
∴k= -
1
2
巩固知识
拓展与应用
1、一次函数y=kx+b中，kb>0,且y随x的增大而
减小，则它的图象大致为（ ）
C
例 题
例1、已知函数y=(m+1)x-3
(1)当m取何值时，y随x的增大而增大？
这时它的图象经过哪些象限
(2)当 m取何值时，y随x的增大而减小？
这时它的图象经过哪些象限
解：
当m+1>0即m>-1时y随x的增大而增大，
当m+1<0即m<-1时y随x的增大而减小，
这时它的图象经过一、三、四象限
这时它的图象经过二、三、四象限
例 题
例2、对于一次函数y=(a+4)x+2a-1,如果
y随x的增大而增大，且它的图象与y轴的
交点在x轴的下方，试求a的取值范围
解：因为y随x的增大而增大，
所以 a+4>0 即 a>-4
又因为它的图象与y轴的交点在x轴的下方
所以 2a-1 < 0 即 a < 1/2
所以 -4 < a < 1/2
例3、已知点(2,m) 、(-3,n)都在直线 上
试比较 m和n的大小。你能想出几种判断的方法
例 题
解：方法一 把两点的坐标代入函数关系式
当 x=2 时, m=4/3 ， 当 x= -3 时, n=1/2
所以 m > n
方法二 因为 K=1/6 >0，所以函数y随x增加而
增加 。从而直接得到 m > n
一次函数的性质
1.在y=kx+b中:
当k＞0,y随x的增大而______;当k＜0,y随x的增大而______.
正比例函数的性质
1.正比例函数y=kx的图象是
经过_________的一条直线;
2.在直线y=k1x+b1与直线y=k2x+b2中，
如果______________,那么这两条直线平行。
2. 1)当 k >0,y=kx经过______象限
2)当 k <0,y=kx经过______象限.
k1 = k2 , b1≠b2
增大
减小
原点(0,0)
一、三
二、四
3.y=kx+b(k≠0)所经过的象限：
k>0,b>0→___ ___ ___
k>0,b<0→___ ___ ___
k<0,b>0→___ ___ ___
k<0,b<0→___ ___ ___
一、三、二
一、三、四
二、四、一
二、四、三