人教版 八年级 上册 数学11.1 --11.3基础练习题(3课时 Word版 含答案)
文档属性
| 名称 | 人教版 八年级 上册 数学11.1 --11.3基础练习题(3课时 Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 494.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 11:39:52 | ||
图片预览




文档简介
人教版
八年级
上册
数学11.1
--11.3基础练习题
11.1与三角形有关的线段
一、选择题
下面几个图形不具有稳定性的是
A.
B.
C.
D.
已知a,b,c是的三条边长,化简的结果为
A.
B.
C.
2c
D.
0
长度分别为2,7,x的三条线段能组成一个三角形,x的值可以是
A.
4
B.
5
C.
6
D.
9
长为9,6,5,4的四根木条,选其中三根组成三角形,选法有
A.
1种
B.
2种
C.
3种
D.
4种
下列各组数中,不可能成为一个三角形三边长的是
A.
2,3,4
B.
5,7,7
C.
5,6,12
D.
6,8,10
如图,在中,,G为AD的中点,延长BG交AC于E,F为AB上一点,于H,下面判断正确的有
是的角平分线;是边AD上的中线;
是边AD上的高;是的角平分线和高.
A.
1个
B.
2个
C.
3个
D.
4个
如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,测得米,米,A、B间的距离不可能是
A.
5米
B.
10米
C.
15米
D.
20米
若a、b、c为的三边长,且满足,则c的值可以为
A.
5
B.
6
C.
7
D.
8
下列说法错误的是
A.
一般锐角三角形的三条高、三条中线、三条角平分线分别交于一点
B.
钝角三角形有两条高在三角形外部
C.
直角三角形只有一条高
D.
任意三角形都有三条高、三条中线、三条角平分线
三角形的高、中线和角平分线都是
??
A.
直线
B.
射线
C.
线段
D.
以上答案都不对
如图,在中,AE是和AF分别是BC边上的中线和高线,AD是的平分线.则下列线段中最短的是
A.
AE
B.
AD
C.
AF
D.
AC
如图,图中直角三角形共有
A.
1个
B.
2个
C.
3个
D.
4个
二、填空题
有四条线段,长分别为3cm、5cm、7cm、9cm,如果用这些线段组成三角形,可以组成______
个三角形.
如图,在中,D,E,F分别是BC,AD,CE的中点,且,则________.
如图,D、E分别是边AB、BC上的点,,,设的面积为,的面积为,若,则的值为__.
如图,在中,,,则以为内角的三角形是__________,以BC为边的三角形是___________,所对的边为___________.
三、解答题
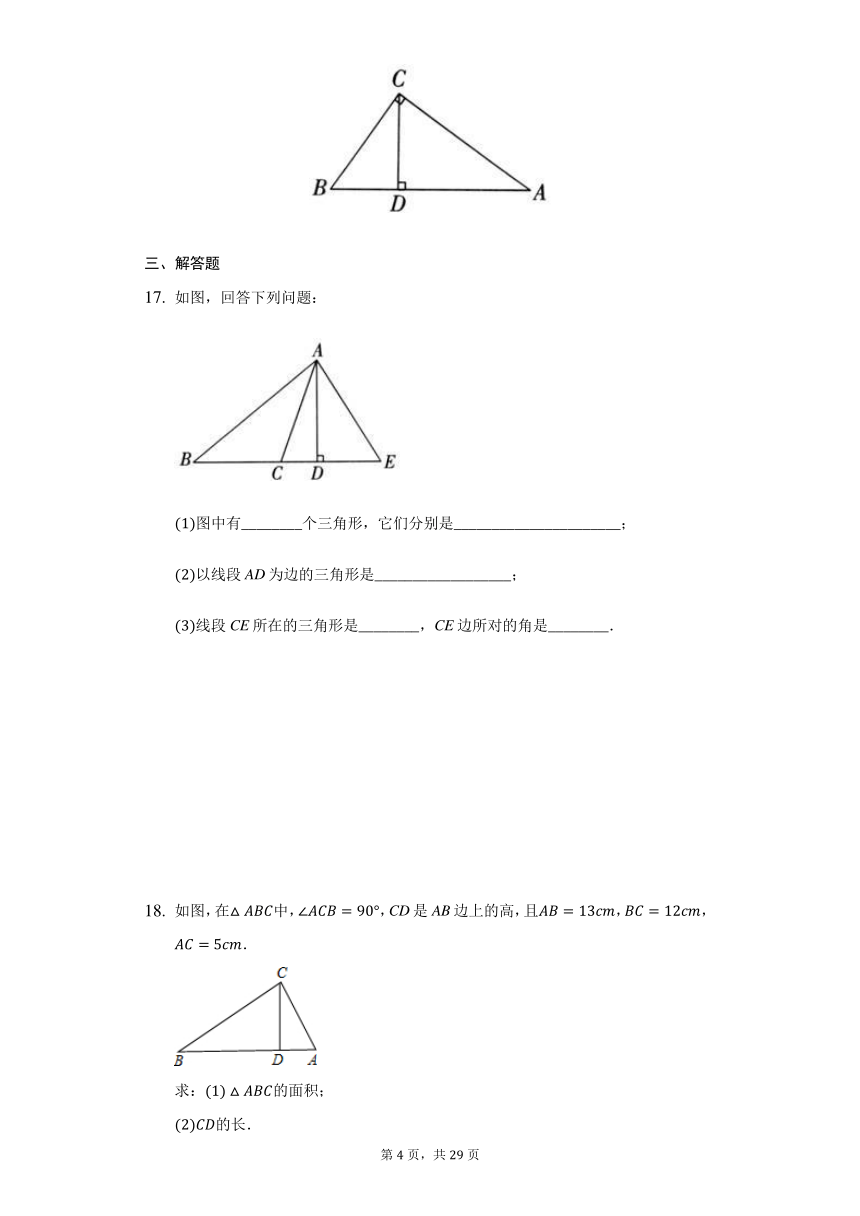
如图,回答下列问题:
图中有________个三角形,它们分别是______________________;
以线段AD为边的三角形是__________________;
线段CE所在的三角形是________,CE边所对的角是________.
如图,在中,,CD是AB边上的高,且,,.
求:的面积;
的长.
已知三角形的三条边为互不相等的整数,且有两边长分别为7和9,另一条边长为偶数.
请写出一个三角形,符合上述条件的第三边长.
若符合上述条件的三角形共有a个,求a的值.
如图,在中,D、E分别是BC,AD的中点,,求.
答案和解析
1.【答案】A
【解答】
解:根据三角形的稳定性可得,B、C、D都具有稳定性.不具有稳定性的是A选项.
故选A.
2.【答案】D
【解答】
解:、b、c为的三条边长,
,,
原式
.
故选D.
3.【答案】C
【解答】
解:由三角形三边关系定理得,即.
因此,本题的第三边应满足,把各项代入不等式符合的即为答案.
4,5,9都不符合不等式,只有6符合不等式,
故选C.
4.【答案】C
【解答】
解:四根木条的所有组合:9,6,5和9,6,4和9,5,4和6,5,4;
根据三角形的三边关系,得能组成三角形的有9,6,5和9,6,4和6,5,4.
故选C.
5.【答案】C
【解析】解:,
三角形三边长为5,6,12不可能成为一个三角形,
故选:C.
6.【答案】B
【解答】
解:根据三角形的角平分线的概念,知AG是的角平分线,故此说法错误;
根据三角形的中线的概念,知BG是的边AD上的中线,故此说法错误;
根据三角形的高的概念,知CH为的边AD上的高,故此说法正确;
根据三角形的角平分线和高的概念,知AH是的角平分线和高线,故此说法正确.
故选B.
7.【答案】A
【解答】
解:连接AB,根据三角形的三边关系定理得:
,
即:,
、B间的距离在5和25之间,
、B间的距离不可能是5米;
故选:A.
8.【答案】A
【解答】
解:,
,;,;
则,
即,
符合条件;
故选A.
9.【答案】C
【解答】解:锐角三角形的三条高线、三条角平分线分别交于一点,故本选项说法正确;
B.钝角三角形有两条高线在三角形的外部,故本选项说法正确;
C.直角三角形也有三条高线,故本选项说法错误;
D.任意三角形都有三条高线、中线、角平分线,故本选项说法正确;
故选C.
10.【答案】C
【解答】
解:三角形的高、中线和角平分线都是线段.
故选C.
11.【答案】C
【解答】
解:在中,AF是高,
,
又在中,AD是的平分线,AE是BC边上的中线,
,,,故最短线段为AF.
故选C.
12.【答案】C
【解析】
【分析】
本题考查了直角三角形的定义,比较简单,掌握直角三角形的定义是关键,要做到不重不漏.
根据直角三角形的定义:有一个角是直角的三角形是直角三角形,可作判断.
【解答】
解:如图,
,
图中直角三角形有、、,共有3个.
故选C.
13.【答案】3
【解析】解:其中的任意三条组合有3、5、7;3、5、9;3、7、9;5、7、9四种情况.
根据三角形的三边关系,则其中的,不能组成三角形,应舍去,
故可以组成3个三角形.
故答案为:3.
根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
此题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.
14.【答案】
【解答】
解:点D,E,F,分别为BC、AD、CE的中点,且,
,
,
,
,
故答案为.
15.【答案】1
【解答】
解:,
,
,
,
.
故答案为1.
16.【答案】和;和;CD和AC.
【解答】
解:以为内角的三角形是和,以BC为边的三角形是和,所对的边为CD和AC,
故答案为和;和;CD和AC.
17.【答案】;,,,,,;
,,;
,.
【解答】
解:图中有6个三角形,它们分别是,,,,,.
故答案为6;,,,,,;
以线段AD为边的三角形是,,.
故答案为,,;
线段CE所在的三角形是,CE边所对的角是.
故答案为,.
18.【答案】解:的面积;
的面积,
.
19.【答案】解:两边长分别为9和7,设第三边是a,则,即.
第三边长是答案不唯一;
,
的值为4,6,8,10,12,14共六个,
;
20.【答案】解:、E分别是BC,AD的中点,,
.
11.2
与三角形有关的角
一、选择题
1.
已知在△ABC中,∠A=70°,∠B=60°,则∠C的度数为( )
A.50°
B.60°
C.70°
D.80°
2.
在△ABC中,∠A,∠C与∠B处的外角的度数如图所示,则x的值是( )
A.80
B.70
C.65
D.60
3.
在Rt△ABC中,∠C=90°,∠A-∠B=50°,则∠A的度数为( )
A.80°
B.70°
C.60°
D.50°
4.
如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )
A.65°
B.70°
C.75°
D.85°
5.
一个三角形三个内角的度数之比为2∶3∶4,这个三角形是( )
A.
直角三角形
B.
等腰三角形
C.
锐角三角形
D.
钝角三角形
6.
若三角形的三个内角的度数之比为2∶3∶7,则这个三角形的最大内角是( )
A.75°
B.90°
C.105°
D.120°
7.
如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为
( )
A.118°
B.119°
C.120°
D.121°
8.
如图,在△ABC中,D是∠ABC和∠ACB的平分线的交点,∠A=80°,∠ABD=30°,则∠BDC的度数为( )
A.100°
B.110°
C.120°
D.130°
9.
如图,把△ABC沿DE折叠,当点A落在四边形BCED内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,这个关系是( )
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
10.
如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是
( )
A.x=y+z
B.x=y-z
C.x=z-y
D.x+y+z=180
二、填空题
11.
如图所示,在△ABC中,∠A=45°,∠B=60°,则外角∠ACD= .
?
12.
有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图所示的方式剪去它的一个角,在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为 .?
13.
如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就可以说明一个几何定理.请你写出这个定理的内容:______________________.
14.
如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E.若∠AFD=158°,则∠EDF= °.
15.
定义:当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么“特征角”α的度数为____________.
16.
如图,在△ABC中,点E在BC的延长线上,∠ABC的平分线与∠ACE的平分线相交于点D.
(1)若∠A=70°,则∠ACE-∠ABC=________°,∠D=________°;
(2)若∠A=α,则∠ACE-∠ABC=________,∠D=________.
三、解答题
17.
如图,用钢筋做支架,要求BA,DC相交所成的锐角为32°,现测得∠BAC=∠DCA=115°,则这个支架符合设计要求吗?为什么?
18.
如图,在△ABC中,AD是BC边上的高,E是AB上一点,CE交AD于点M,且∠DCM=∠MAE.
求证:△ACE是直角三角形.
19.
在△ABC中,∠B=55°,且3∠A=∠B+∠C,求∠A和∠C的度数.
20.
如图,在△ABC中,CD,BE分别是AB,AC边上的高,BE,CD相交于点O.
(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)求证:∠BOC+∠A=180°.
人教版
八年级数学上册
11.2
与三角形有关的角
同步培优训练-答案
一、选择题
1.
【答案】A
2.
【答案】B
3.
【答案】B 又∵∠A-∠B=50°,∴2∠A=140°.
∴∠A=70°.
4.
【答案】B ∴∠CFD=∠AFE=55°.
∴∠ACB=∠D+∠CFD=15°+55°=70°.
5.
【答案】
C
6.
【答案】C 由题意,得2x+3x+7x=180°,解得x=15°.
∴7x=105°.
7.
【答案】C ∴∠ACB=180°-∠A-∠ABC=78°.
∵∠ABC,∠ACB的平分线分别为BE,CD,
∴∠FBC=∠ABC=21°,∠FCB=∠ACB=39°,
∴∠BFC=180°-∠FBC-∠FCB=120°.
故选C.
8.
【答案】D ∴∠DBC=∠ABD=30°,∠ABC=2∠ABD=2×30°=60°.
∴∠ACB=180°-∠A-∠ABC=40°.
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°.
∴∠BDC=180°-∠DCB-∠DBC=130°.
9.
【答案】B
10.
【答案】A
二、填空题
11.
【答案】
105°
12.
【答案】105° 所以∠1+∠2=360°-90°=270°.
因为∠1=165°,
所以∠2的度数为105°.
13.
【答案】三角形三个内角的和等于180°
14.
【答案】68 ∴∠CFD=180°-∠AFD=180°-158°=22°.
∵FD⊥BC,
∴∠FDC=90°.
∴∠C=180°-∠FDC-∠CFD=180°-90°-22°=68°.
∵∠B=∠C,DE⊥AB,
∴∠EDB=180°-∠B-∠DEB=180°-68°-90°=22°.
∴∠EDF=180°-90°-22°=68°.
15.
【答案】48°或96°或88° 当β=48°时,则“特征角”α=2×48°=96°;
当第三个角为48°时,α+α+48°=180°,解得α=88°.
综上所述,“特征角”α的度数为48°或96°或88°.
16.
【答案】(1)70 35 (2)α α
三、解答题
17.
【答案】
解:这个支架不符合设计要求.
理由:如图,延长BA,DC交于点E.
∵∠BAC=∠DCA=115°,
∴∠EAC=∠ECA=65°.
∴∠E=180°-∠EAC-∠ECA=50°.
∵要求BA,DC相交所成的锐角为32°,
∴这个支架不符合设计要求.
18.
【答案】
证明:∵AD是BC边上的高,
∴∠ADC=90°.
∵∠DCM=∠MAE,∠CMD=∠AME,
∴∠AEC=∠ADC=90°.
∴△ACE是直角三角形.
19.
【答案】
解:∵在△ABC中,∠A+∠B+∠C=180°,3∠A=∠B+∠C,
∴4∠A=180°,
解得∠A=45°.
∵∠B=55°,∴∠C=180°-45°-55°=80°.
20.
【答案】
解:(1)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠BEC=90°.
∵∠ABC=50°,∠ACB=60°.
∴∠BCO=40°,∠CBO=30°.
∴∠BOC=180°-40°-30°=110°.
(2)证明:∵CD⊥AB,BE⊥AC,
∴∠BDC=∠BEC=90°.
∴∠ABE=90°-∠A.
∴∠BOC=∠ABE+∠BDC=90°-∠A+90°=180°-∠A.
∴∠BOC+∠A=180°.
11.3多边形及其内角和
一.选择题
1.正多边形的每个内角为135度,则多边形为( )
A.4
B.6
C.8
D.10
2.若一个多边形减去一个角后,内角和为720°,则原多边形不可能是几边形( )
A.四边形
B.五边形
C.六边形
D.七边形
3.一个四边形的四个内角度数之比为1:2:4:5,则这个四边形中,最小的内角为( )
A.30°
B.40°
C.50°
D.60°
4.一个正多边形的每个内角的度数都等于相邻外角的2倍,则该正多边形的边数是( )
A.3
B.4
C.6
D.12
5.如图,已知一个五边形ABCDE纸片,一条直线将该纸片分割成两个多边形.若这两个多边形内角和分别为m和n,则m+n不可能是( )
A.540°
B.720°
C.900°
D.1080°
6.如图,在五边形ABCDE中,AE∥BC,延长DE至点F,连接BE,若∠A=∠C,∠1=∠3,∠AEF=2∠2,则下列结论正确的是( )
①∠1=∠2
②AB∥CD
③∠AED=∠A
④CD⊥DE
A.1个
B.2个
C.3个
D.4个
7.如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α
(0°<α<90°),若DE⊥B′C′,则∠α为( )
A.36°
B.54°
C.60°
D.72°
8.如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=210°,则∠P=( )
A.10°
B.15°
C.30°
D.40°
9.设BF交AC于点P,AE交DF于点Q.若∠APB=126°,∠AQF=100°,则∠A-∠F=( )
A.60°
B.46°
C.26°
D.45°
10.如图,已知四边形ABCD中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.90°
B.135°
C.270°
D.315°
11.如图,在六边形ABCDEF中,若∠A+∠B+∠C+∠D=500°,∠DEF与∠AFE的平分线交于点G,则∠G等于( )
A.55°
B.65°
C.70°
D.80°
12.如图,A,B,C,D,E,F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
A.180°
B.360°
C.540°
D.720°
二.填空题
13.八边形的内角和为
;一个多边形的每个内角都是120°,则它是
边形.
14.一个多边形,除了一个内角外,其余各角的和为2750°,则内角和是
.
15.如图,已知在四边形ABCD中,∠A+∠C=135°,∠ADE=125°,则∠B=
.
16.如图所示,若∠DBE=78°,则∠A+∠C+∠D+∠E=
°.
17.如图所示,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
°.
三.解答题
18.(1)已知一个正多边形的每个内角比它的每个外角的4倍多30°,求这个多边形的边数;
(2)一个多边形的外角和是内角和的七分之二,求这个多边形的边数.
19.如图,在四边形ABCD中,BD⊥CD,EF⊥CD,且∠1=∠2.
(1)求证:AD∥BC;
(2)若BD平分∠ABC,∠A=130°,求∠C的度数.
20.如图,四边形ABCD中,∠BAD=106°,∠BCD=64°,点M,N分别在AB,BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC.
求(1)∠F的度数;
(2)∠D的度数.
21.将纸片△ABC沿DE折叠使点A落在点A'处
【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是
;
【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.
【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为
.
22.已知,在四边形ABCD中,∠A+∠C=160°,BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线.
(1)如图1,若BE∥DF,求∠C的度数;
(2)如图2,若BE,DF交于点G,且BE∥AD,DF∥AB,求∠C的度数.
参考答案
1-5:CAACD
6-10:CBBBC
11-12:CB
13、1080°;六
14、2880°
15、170°
16、102
17、720
18、:(1)设这个多边形的每个内角是x°,每个外角是y°,
则得到一个方程组
得
而任何多边形的外角和是360°,
则多边形内角和中的外角的个数是360÷30=12,
则这个多边形的边数是12边形;
(2)设这个多边形的边数为n,
依题意得:(n-2)180°=360°,
解得n=9,
答:这个多边形的边数为9.
19、:(1)证明:∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(垂直于同一直线的两条直线平行),
∴∠2=∠3(两直线平行,同位角相等).
∵∠1=∠2,
∴∠1=∠3(等量代换).
∴AD∥BC(内错角相等,两直线平行).
(2)∵AD∥BC(已知),
∴∠ABC+∠A=180°(两直线平行,同旁内角互补).
∵∠A=130°(已知),
∴∠ABC=50°.
∵DB平分∠ABC(已知),
∴∠3=25°.
∴∠C=90°-∠3=65°.
20、:(1)∵MF∥AD,FN∥DC,∠BAD=106°,∠BCD=64°,
∴∠BMF=106°,∠FNB=64°,
∵将△BMN沿MN翻折,得△FMN,
∴∠FMN=∠BMN=53°,∠FNM=∠MNB=32°,
∴∠F=∠B=180°-53°-32°=95°;
(2)∠F=∠B=95°,
∠D=360°-106°-64°-95°=95°.
21、:(1)如图,∠1=2∠A.
理由如下:由折叠知识可得:∠EA′D=∠A;
∵∠1=∠A+∠EA′D,
∴∠1=2∠A.
(2)如图②,2∠A=∠1+∠2.
理由如下:∵∠1+∠A′DA+∠2+∠A′EA=360°,
∠A+∠A′+∠A′DA+∠A′EA=360°,
∴∠A′+∠A=∠1+∠2,
由折叠知识可得:∠A=∠A′,
∴2∠A=∠1+∠2.
(3)如图③,
∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A+∠2,
∴2∠A=∠1-∠2=56°,
解得∠A=28°.
故答案为:∠1=2∠A;28°.
22、:(1)过点C作CH∥DF,
∵BE∥DF,
∴BE∥DF∥CH,
∴∠FDC=∠DCH,∠BCH=∠EBC,
∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC,
∵BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线,
∴∠FDC=∠CDM,∠EBC=∠CBN,
∵∠A+∠BCD=160°,
∴∠ADC+∠ABC=360°160°=200°,
∴∠MDC+∠CBN=160°,
∴∠FDC+∠CBE=80°,
∴∠DCB=80°;
(2)连接GC并延长,
同理得∠MDC+∠CBN=160°,∠MDF+∠NBG=80°,
∵BE∥AD,DF∥AB,
∴∠A=∠MDF=∠DGB=∠NBG=40°,
∵∠A+∠BCD=160°,
∴∠BCD=160°-40°=120°.
第2页,共2页
第1页,共1页
八年级
上册
数学11.1
--11.3基础练习题
11.1与三角形有关的线段
一、选择题
下面几个图形不具有稳定性的是
A.
B.
C.
D.
已知a,b,c是的三条边长,化简的结果为
A.
B.
C.
2c
D.
0
长度分别为2,7,x的三条线段能组成一个三角形,x的值可以是
A.
4
B.
5
C.
6
D.
9
长为9,6,5,4的四根木条,选其中三根组成三角形,选法有
A.
1种
B.
2种
C.
3种
D.
4种
下列各组数中,不可能成为一个三角形三边长的是
A.
2,3,4
B.
5,7,7
C.
5,6,12
D.
6,8,10
如图,在中,,G为AD的中点,延长BG交AC于E,F为AB上一点,于H,下面判断正确的有
是的角平分线;是边AD上的中线;
是边AD上的高;是的角平分线和高.
A.
1个
B.
2个
C.
3个
D.
4个
如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,测得米,米,A、B间的距离不可能是
A.
5米
B.
10米
C.
15米
D.
20米
若a、b、c为的三边长,且满足,则c的值可以为
A.
5
B.
6
C.
7
D.
8
下列说法错误的是
A.
一般锐角三角形的三条高、三条中线、三条角平分线分别交于一点
B.
钝角三角形有两条高在三角形外部
C.
直角三角形只有一条高
D.
任意三角形都有三条高、三条中线、三条角平分线
三角形的高、中线和角平分线都是
??
A.
直线
B.
射线
C.
线段
D.
以上答案都不对
如图,在中,AE是和AF分别是BC边上的中线和高线,AD是的平分线.则下列线段中最短的是
A.
AE
B.
AD
C.
AF
D.
AC
如图,图中直角三角形共有
A.
1个
B.
2个
C.
3个
D.
4个
二、填空题
有四条线段,长分别为3cm、5cm、7cm、9cm,如果用这些线段组成三角形,可以组成______
个三角形.
如图,在中,D,E,F分别是BC,AD,CE的中点,且,则________.
如图,D、E分别是边AB、BC上的点,,,设的面积为,的面积为,若,则的值为__.
如图,在中,,,则以为内角的三角形是__________,以BC为边的三角形是___________,所对的边为___________.
三、解答题
如图,回答下列问题:
图中有________个三角形,它们分别是______________________;
以线段AD为边的三角形是__________________;
线段CE所在的三角形是________,CE边所对的角是________.
如图,在中,,CD是AB边上的高,且,,.
求:的面积;
的长.
已知三角形的三条边为互不相等的整数,且有两边长分别为7和9,另一条边长为偶数.
请写出一个三角形,符合上述条件的第三边长.
若符合上述条件的三角形共有a个,求a的值.
如图,在中,D、E分别是BC,AD的中点,,求.
答案和解析
1.【答案】A
【解答】
解:根据三角形的稳定性可得,B、C、D都具有稳定性.不具有稳定性的是A选项.
故选A.
2.【答案】D
【解答】
解:、b、c为的三条边长,
,,
原式
.
故选D.
3.【答案】C
【解答】
解:由三角形三边关系定理得,即.
因此,本题的第三边应满足,把各项代入不等式符合的即为答案.
4,5,9都不符合不等式,只有6符合不等式,
故选C.
4.【答案】C
【解答】
解:四根木条的所有组合:9,6,5和9,6,4和9,5,4和6,5,4;
根据三角形的三边关系,得能组成三角形的有9,6,5和9,6,4和6,5,4.
故选C.
5.【答案】C
【解析】解:,
三角形三边长为5,6,12不可能成为一个三角形,
故选:C.
6.【答案】B
【解答】
解:根据三角形的角平分线的概念,知AG是的角平分线,故此说法错误;
根据三角形的中线的概念,知BG是的边AD上的中线,故此说法错误;
根据三角形的高的概念,知CH为的边AD上的高,故此说法正确;
根据三角形的角平分线和高的概念,知AH是的角平分线和高线,故此说法正确.
故选B.
7.【答案】A
【解答】
解:连接AB,根据三角形的三边关系定理得:
,
即:,
、B间的距离在5和25之间,
、B间的距离不可能是5米;
故选:A.
8.【答案】A
【解答】
解:,
,;,;
则,
即,
符合条件;
故选A.
9.【答案】C
【解答】解:锐角三角形的三条高线、三条角平分线分别交于一点,故本选项说法正确;
B.钝角三角形有两条高线在三角形的外部,故本选项说法正确;
C.直角三角形也有三条高线,故本选项说法错误;
D.任意三角形都有三条高线、中线、角平分线,故本选项说法正确;
故选C.
10.【答案】C
【解答】
解:三角形的高、中线和角平分线都是线段.
故选C.
11.【答案】C
【解答】
解:在中,AF是高,
,
又在中,AD是的平分线,AE是BC边上的中线,
,,,故最短线段为AF.
故选C.
12.【答案】C
【解析】
【分析】
本题考查了直角三角形的定义,比较简单,掌握直角三角形的定义是关键,要做到不重不漏.
根据直角三角形的定义:有一个角是直角的三角形是直角三角形,可作判断.
【解答】
解:如图,
,
图中直角三角形有、、,共有3个.
故选C.
13.【答案】3
【解析】解:其中的任意三条组合有3、5、7;3、5、9;3、7、9;5、7、9四种情况.
根据三角形的三边关系,则其中的,不能组成三角形,应舍去,
故可以组成3个三角形.
故答案为:3.
根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
此题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.
14.【答案】
【解答】
解:点D,E,F,分别为BC、AD、CE的中点,且,
,
,
,
,
故答案为.
15.【答案】1
【解答】
解:,
,
,
,
.
故答案为1.
16.【答案】和;和;CD和AC.
【解答】
解:以为内角的三角形是和,以BC为边的三角形是和,所对的边为CD和AC,
故答案为和;和;CD和AC.
17.【答案】;,,,,,;
,,;
,.
【解答】
解:图中有6个三角形,它们分别是,,,,,.
故答案为6;,,,,,;
以线段AD为边的三角形是,,.
故答案为,,;
线段CE所在的三角形是,CE边所对的角是.
故答案为,.
18.【答案】解:的面积;
的面积,
.
19.【答案】解:两边长分别为9和7,设第三边是a,则,即.
第三边长是答案不唯一;
,
的值为4,6,8,10,12,14共六个,
;
20.【答案】解:、E分别是BC,AD的中点,,
.
11.2
与三角形有关的角
一、选择题
1.
已知在△ABC中,∠A=70°,∠B=60°,则∠C的度数为( )
A.50°
B.60°
C.70°
D.80°
2.
在△ABC中,∠A,∠C与∠B处的外角的度数如图所示,则x的值是( )
A.80
B.70
C.65
D.60
3.
在Rt△ABC中,∠C=90°,∠A-∠B=50°,则∠A的度数为( )
A.80°
B.70°
C.60°
D.50°
4.
如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )
A.65°
B.70°
C.75°
D.85°
5.
一个三角形三个内角的度数之比为2∶3∶4,这个三角形是( )
A.
直角三角形
B.
等腰三角形
C.
锐角三角形
D.
钝角三角形
6.
若三角形的三个内角的度数之比为2∶3∶7,则这个三角形的最大内角是( )
A.75°
B.90°
C.105°
D.120°
7.
如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为
( )
A.118°
B.119°
C.120°
D.121°
8.
如图,在△ABC中,D是∠ABC和∠ACB的平分线的交点,∠A=80°,∠ABD=30°,则∠BDC的度数为( )
A.100°
B.110°
C.120°
D.130°
9.
如图,把△ABC沿DE折叠,当点A落在四边形BCED内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,这个关系是( )
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
10.
如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是
( )
A.x=y+z
B.x=y-z
C.x=z-y
D.x+y+z=180
二、填空题
11.
如图所示,在△ABC中,∠A=45°,∠B=60°,则外角∠ACD= .
?
12.
有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图所示的方式剪去它的一个角,在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为 .?
13.
如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就可以说明一个几何定理.请你写出这个定理的内容:______________________.
14.
如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E.若∠AFD=158°,则∠EDF= °.
15.
定义:当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么“特征角”α的度数为____________.
16.
如图,在△ABC中,点E在BC的延长线上,∠ABC的平分线与∠ACE的平分线相交于点D.
(1)若∠A=70°,则∠ACE-∠ABC=________°,∠D=________°;
(2)若∠A=α,则∠ACE-∠ABC=________,∠D=________.
三、解答题
17.
如图,用钢筋做支架,要求BA,DC相交所成的锐角为32°,现测得∠BAC=∠DCA=115°,则这个支架符合设计要求吗?为什么?
18.
如图,在△ABC中,AD是BC边上的高,E是AB上一点,CE交AD于点M,且∠DCM=∠MAE.
求证:△ACE是直角三角形.
19.
在△ABC中,∠B=55°,且3∠A=∠B+∠C,求∠A和∠C的度数.
20.
如图,在△ABC中,CD,BE分别是AB,AC边上的高,BE,CD相交于点O.
(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)求证:∠BOC+∠A=180°.
人教版
八年级数学上册
11.2
与三角形有关的角
同步培优训练-答案
一、选择题
1.
【答案】A
2.
【答案】B
3.
【答案】B 又∵∠A-∠B=50°,∴2∠A=140°.
∴∠A=70°.
4.
【答案】B ∴∠CFD=∠AFE=55°.
∴∠ACB=∠D+∠CFD=15°+55°=70°.
5.
【答案】
C
6.
【答案】C 由题意,得2x+3x+7x=180°,解得x=15°.
∴7x=105°.
7.
【答案】C ∴∠ACB=180°-∠A-∠ABC=78°.
∵∠ABC,∠ACB的平分线分别为BE,CD,
∴∠FBC=∠ABC=21°,∠FCB=∠ACB=39°,
∴∠BFC=180°-∠FBC-∠FCB=120°.
故选C.
8.
【答案】D ∴∠DBC=∠ABD=30°,∠ABC=2∠ABD=2×30°=60°.
∴∠ACB=180°-∠A-∠ABC=40°.
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°.
∴∠BDC=180°-∠DCB-∠DBC=130°.
9.
【答案】B
10.
【答案】A
二、填空题
11.
【答案】
105°
12.
【答案】105° 所以∠1+∠2=360°-90°=270°.
因为∠1=165°,
所以∠2的度数为105°.
13.
【答案】三角形三个内角的和等于180°
14.
【答案】68 ∴∠CFD=180°-∠AFD=180°-158°=22°.
∵FD⊥BC,
∴∠FDC=90°.
∴∠C=180°-∠FDC-∠CFD=180°-90°-22°=68°.
∵∠B=∠C,DE⊥AB,
∴∠EDB=180°-∠B-∠DEB=180°-68°-90°=22°.
∴∠EDF=180°-90°-22°=68°.
15.
【答案】48°或96°或88° 当β=48°时,则“特征角”α=2×48°=96°;
当第三个角为48°时,α+α+48°=180°,解得α=88°.
综上所述,“特征角”α的度数为48°或96°或88°.
16.
【答案】(1)70 35 (2)α α
三、解答题
17.
【答案】
解:这个支架不符合设计要求.
理由:如图,延长BA,DC交于点E.
∵∠BAC=∠DCA=115°,
∴∠EAC=∠ECA=65°.
∴∠E=180°-∠EAC-∠ECA=50°.
∵要求BA,DC相交所成的锐角为32°,
∴这个支架不符合设计要求.
18.
【答案】
证明:∵AD是BC边上的高,
∴∠ADC=90°.
∵∠DCM=∠MAE,∠CMD=∠AME,
∴∠AEC=∠ADC=90°.
∴△ACE是直角三角形.
19.
【答案】
解:∵在△ABC中,∠A+∠B+∠C=180°,3∠A=∠B+∠C,
∴4∠A=180°,
解得∠A=45°.
∵∠B=55°,∴∠C=180°-45°-55°=80°.
20.
【答案】
解:(1)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠BEC=90°.
∵∠ABC=50°,∠ACB=60°.
∴∠BCO=40°,∠CBO=30°.
∴∠BOC=180°-40°-30°=110°.
(2)证明:∵CD⊥AB,BE⊥AC,
∴∠BDC=∠BEC=90°.
∴∠ABE=90°-∠A.
∴∠BOC=∠ABE+∠BDC=90°-∠A+90°=180°-∠A.
∴∠BOC+∠A=180°.
11.3多边形及其内角和
一.选择题
1.正多边形的每个内角为135度,则多边形为( )
A.4
B.6
C.8
D.10
2.若一个多边形减去一个角后,内角和为720°,则原多边形不可能是几边形( )
A.四边形
B.五边形
C.六边形
D.七边形
3.一个四边形的四个内角度数之比为1:2:4:5,则这个四边形中,最小的内角为( )
A.30°
B.40°
C.50°
D.60°
4.一个正多边形的每个内角的度数都等于相邻外角的2倍,则该正多边形的边数是( )
A.3
B.4
C.6
D.12
5.如图,已知一个五边形ABCDE纸片,一条直线将该纸片分割成两个多边形.若这两个多边形内角和分别为m和n,则m+n不可能是( )
A.540°
B.720°
C.900°
D.1080°
6.如图,在五边形ABCDE中,AE∥BC,延长DE至点F,连接BE,若∠A=∠C,∠1=∠3,∠AEF=2∠2,则下列结论正确的是( )
①∠1=∠2
②AB∥CD
③∠AED=∠A
④CD⊥DE
A.1个
B.2个
C.3个
D.4个
7.如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α
(0°<α<90°),若DE⊥B′C′,则∠α为( )
A.36°
B.54°
C.60°
D.72°
8.如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=210°,则∠P=( )
A.10°
B.15°
C.30°
D.40°
9.设BF交AC于点P,AE交DF于点Q.若∠APB=126°,∠AQF=100°,则∠A-∠F=( )
A.60°
B.46°
C.26°
D.45°
10.如图,已知四边形ABCD中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.90°
B.135°
C.270°
D.315°
11.如图,在六边形ABCDEF中,若∠A+∠B+∠C+∠D=500°,∠DEF与∠AFE的平分线交于点G,则∠G等于( )
A.55°
B.65°
C.70°
D.80°
12.如图,A,B,C,D,E,F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
A.180°
B.360°
C.540°
D.720°
二.填空题
13.八边形的内角和为
;一个多边形的每个内角都是120°,则它是
边形.
14.一个多边形,除了一个内角外,其余各角的和为2750°,则内角和是
.
15.如图,已知在四边形ABCD中,∠A+∠C=135°,∠ADE=125°,则∠B=
.
16.如图所示,若∠DBE=78°,则∠A+∠C+∠D+∠E=
°.
17.如图所示,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
°.
三.解答题
18.(1)已知一个正多边形的每个内角比它的每个外角的4倍多30°,求这个多边形的边数;
(2)一个多边形的外角和是内角和的七分之二,求这个多边形的边数.
19.如图,在四边形ABCD中,BD⊥CD,EF⊥CD,且∠1=∠2.
(1)求证:AD∥BC;
(2)若BD平分∠ABC,∠A=130°,求∠C的度数.
20.如图,四边形ABCD中,∠BAD=106°,∠BCD=64°,点M,N分别在AB,BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC.
求(1)∠F的度数;
(2)∠D的度数.
21.将纸片△ABC沿DE折叠使点A落在点A'处
【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是
;
【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.
【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为
.
22.已知,在四边形ABCD中,∠A+∠C=160°,BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线.
(1)如图1,若BE∥DF,求∠C的度数;
(2)如图2,若BE,DF交于点G,且BE∥AD,DF∥AB,求∠C的度数.
参考答案
1-5:CAACD
6-10:CBBBC
11-12:CB
13、1080°;六
14、2880°
15、170°
16、102
17、720
18、:(1)设这个多边形的每个内角是x°,每个外角是y°,
则得到一个方程组
得
而任何多边形的外角和是360°,
则多边形内角和中的外角的个数是360÷30=12,
则这个多边形的边数是12边形;
(2)设这个多边形的边数为n,
依题意得:(n-2)180°=360°,
解得n=9,
答:这个多边形的边数为9.
19、:(1)证明:∵BD⊥CD,EF⊥CD(已知),
∴BD∥EF(垂直于同一直线的两条直线平行),
∴∠2=∠3(两直线平行,同位角相等).
∵∠1=∠2,
∴∠1=∠3(等量代换).
∴AD∥BC(内错角相等,两直线平行).
(2)∵AD∥BC(已知),
∴∠ABC+∠A=180°(两直线平行,同旁内角互补).
∵∠A=130°(已知),
∴∠ABC=50°.
∵DB平分∠ABC(已知),
∴∠3=25°.
∴∠C=90°-∠3=65°.
20、:(1)∵MF∥AD,FN∥DC,∠BAD=106°,∠BCD=64°,
∴∠BMF=106°,∠FNB=64°,
∵将△BMN沿MN翻折,得△FMN,
∴∠FMN=∠BMN=53°,∠FNM=∠MNB=32°,
∴∠F=∠B=180°-53°-32°=95°;
(2)∠F=∠B=95°,
∠D=360°-106°-64°-95°=95°.
21、:(1)如图,∠1=2∠A.
理由如下:由折叠知识可得:∠EA′D=∠A;
∵∠1=∠A+∠EA′D,
∴∠1=2∠A.
(2)如图②,2∠A=∠1+∠2.
理由如下:∵∠1+∠A′DA+∠2+∠A′EA=360°,
∠A+∠A′+∠A′DA+∠A′EA=360°,
∴∠A′+∠A=∠1+∠2,
由折叠知识可得:∠A=∠A′,
∴2∠A=∠1+∠2.
(3)如图③,
∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A+∠2,
∴2∠A=∠1-∠2=56°,
解得∠A=28°.
故答案为:∠1=2∠A;28°.
22、:(1)过点C作CH∥DF,
∵BE∥DF,
∴BE∥DF∥CH,
∴∠FDC=∠DCH,∠BCH=∠EBC,
∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC,
∵BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线,
∴∠FDC=∠CDM,∠EBC=∠CBN,
∵∠A+∠BCD=160°,
∴∠ADC+∠ABC=360°160°=200°,
∴∠MDC+∠CBN=160°,
∴∠FDC+∠CBE=80°,
∴∠DCB=80°;
(2)连接GC并延长,
同理得∠MDC+∠CBN=160°,∠MDF+∠NBG=80°,
∵BE∥AD,DF∥AB,
∴∠A=∠MDF=∠DGB=∠NBG=40°,
∵∠A+∠BCD=160°,
∴∠BCD=160°-40°=120°.
第2页,共2页
第1页,共1页
