人教版九年级数学上册 24.2.2第3课时切线的性质课件(共17张PPT)
文档属性
| 名称 | 人教版九年级数学上册 24.2.2第3课时切线的性质课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 235.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 12:52:09 | ||
图片预览






文档简介
(共17张PPT)
第二十四章
圆
24.2.2直线和圆的位置关系
第3课时
切线的性质
灵宝市秦岭学校
九年级数学组
人教版数学九年级上册
1
理解并掌握圆的切线性质定理.(重点)
2
能运用圆的切线性质定理解决问题.(难点)
学习目标
知识回顾
定义法:与圆只有一个公共点的直线是圆的切线
数量关系法:到圆心的距离等于半径的直线是圆的切线
判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线
1.判定一条直线是圆的切线有哪几种方法?
2.切线判定证明常用辅助线作法有哪几种?
公共点明确:连半径,证垂直。
公共点不明确:作垂直,证半径。
一、圆的切线的性质定理
A
B
C
思考:如图,如果直线BC是⊙O的切线,点A为切点,那么连接OA,OA与BC有怎样的位置关系?
O
BC⊥OA
观察
猜想
圆的切线垂直于经过切点的半径?
思考:如图,如果直线BC是⊙O的切线,点A为切点,那么连接OA,OA与BC有怎样的位置关系?
一、圆的切线的性质定理
O
验证
假设BC与OA不垂直,
过点O作OM⊥BC,垂足为M,
∴BC与⊙O相交.
这与已知条件“直线BC是⊙O的切线”相矛盾.
∴BC⊥OA
反证法.
则OM即圆心到直线BC的距离小于⊙O的半径
M
A
B
C
一、圆的切线的性质定理
归纳
圆的切线性质定理
A
O
B
C
圆的切线垂直于经过切点的半径。
几何语言
∵BC与⊙O相切于点
A
OA是半径
∴
BC⊥OA
一、圆的切线的性质定理
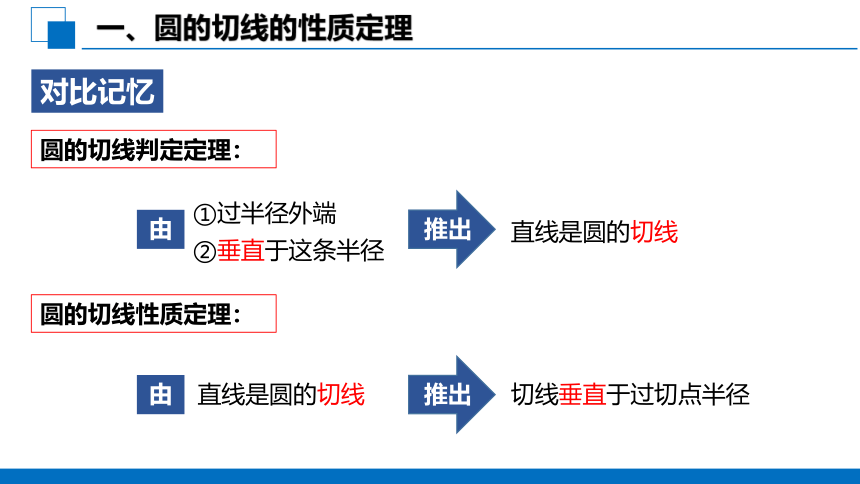
圆的切线判定定理:
圆的切线性质定理:
对比记忆
①过半径外端
②垂直于这条半径
直线是圆的切线
推出
由
直线是圆的切线
切线垂直于过切点半径
推出
由
课堂展示
2.如图,在⊙O中,OA、OB为半径,直线MN与⊙O相切于点B,若∠ABN=30°,
则∠AOB=
.
O
M
B
A
N
60°
1.如图,
PA切半圆⊙O于点A,如果∠P=35°,那么∠
AOP=
.
A
P
O
55°
例题精讲
C
证明:连接OC
∵DE切⊙O于点C
∴OC⊥DE
∴∠OCD=90°
又∵∠COB=2∠A,∠A=32°
∴∠COB=64°
∴∠D=∠OCD-∠COB
=26°
例1:AB是⊙O的直径,点D在AB的延长线上,DE切⊙O于点C,若∠A=32°,求∠D的度数。
方法总结:利用切线的性质解题时,常连接圆心与切点,构造直角三角形,利用直角三角形相关性质解题.
变式训练
∴
1.如图,AB为⊙O的直径,D为AB延长线上一点,DC与⊙O相切于点C,∠DAC=30°,
若⊙O的半径长1cm,则CD=
cm.
O
A
B
D
C
分析:连接OC,则OC⊥DE
又∵∠COB=2∠A=60°
∴∠D=∠OCD-∠COB=30°
∴CD=
OC=
变式训练
O
A
B
C
D
2.如图,AB是⊙O的直径,DC切⊙O于点C,连结CA,CB,如果AB=12cm,
∠ACD=30°,求AC的长和∠B的度数。
证明:连接OC
∵DE切⊙O于点C
∴OC⊥DE
∴∠OCD=90°
又∵∠ACD=30°
∴∠ACO=60°
又∵OA=OC
∴△AOC是等边三角形
∴AB=2AC,∠AOC=60°
∴AC=6cm,∠B=30°
变式训练
3.如图,在☉O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为(
)
A.40°
B.35°
C.30°
D.45°
C
O
A
B
C
D
P
二、圆的切线的判定和性质综合运用
例2:如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.
求证:CD与⊙O相切.
证明:连接OM,过点O作ON⊥CD于点N,
∵⊙O与BC相切于点M,
∴OM⊥BC.
又∵ON⊥CD,
O为正方形ABCD对角线AC上一点,
∴OM=ON,
∴CD与⊙O相切.
M
N
课堂小结
圆的切线的性质
圆的切线垂直于经过切点的半径
性质定理
辅助线作法
见切线,连过切点的半径,得垂直.
1.PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点(不与点A
、B
重合),若∠APB=40°,
求∠ACB的度数.
课堂检测
B
A
O
P
C
证明:连接OA,OB
∵PA、PB切⊙O于A、B
∴∠OAP=∠OBP=90°
又∵∠APB=40°
∴∠AOB=140°
∴∠ACB=70°
课堂检测
2.如图,AB为⊙O的直径,C为⊙O上的一点,AD和过C点的切线互相垂直,垂足为D。求证:AC平分∠DAB
D
A
B
C
O
证明:连接OC
∵CD切⊙O于点C
∴OC⊥CD
又∵AD⊥CD
∴AD∥OC
∴∠CAD=∠OCA
又∵OA=OC
∴∠OAC=∠OCA
∴∠OAC=∠CAD
即:AC平分∠DAB
课堂检测
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作⊙O的切线交AC于点D,试判断△AED的形状,并说明理由.
D
A
B
C
O
E
解:△AED是直角三角形,理由如下:
连接OE
∵AE平分∠BAC
∴∠CAE=∠OAE
又∵OA=OE
∴∠OAE=∠OEA
∴∠OEA=∠CAE
∴AD∥OE
又∵DE切⊙O于点E
∴OE⊥DE
∴AD⊥DE
∴△AED是直角三角形
第二十四章
圆
24.2.2直线和圆的位置关系
第3课时
切线的性质
灵宝市秦岭学校
九年级数学组
人教版数学九年级上册
1
理解并掌握圆的切线性质定理.(重点)
2
能运用圆的切线性质定理解决问题.(难点)
学习目标
知识回顾
定义法:与圆只有一个公共点的直线是圆的切线
数量关系法:到圆心的距离等于半径的直线是圆的切线
判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线
1.判定一条直线是圆的切线有哪几种方法?
2.切线判定证明常用辅助线作法有哪几种?
公共点明确:连半径,证垂直。
公共点不明确:作垂直,证半径。
一、圆的切线的性质定理
A
B
C
思考:如图,如果直线BC是⊙O的切线,点A为切点,那么连接OA,OA与BC有怎样的位置关系?
O
BC⊥OA
观察
猜想
圆的切线垂直于经过切点的半径?
思考:如图,如果直线BC是⊙O的切线,点A为切点,那么连接OA,OA与BC有怎样的位置关系?
一、圆的切线的性质定理
O
验证
假设BC与OA不垂直,
过点O作OM⊥BC,垂足为M,
∴BC与⊙O相交.
这与已知条件“直线BC是⊙O的切线”相矛盾.
∴BC⊥OA
反证法.
则OM
M
A
B
C
一、圆的切线的性质定理
归纳
圆的切线性质定理
A
O
B
C
圆的切线垂直于经过切点的半径。
几何语言
∵BC与⊙O相切于点
A
OA是半径
∴
BC⊥OA
一、圆的切线的性质定理
圆的切线判定定理:
圆的切线性质定理:
对比记忆
①过半径外端
②垂直于这条半径
直线是圆的切线
推出
由
直线是圆的切线
切线垂直于过切点半径
推出
由
课堂展示
2.如图,在⊙O中,OA、OB为半径,直线MN与⊙O相切于点B,若∠ABN=30°,
则∠AOB=
.
O
M
B
A
N
60°
1.如图,
PA切半圆⊙O于点A,如果∠P=35°,那么∠
AOP=
.
A
P
O
55°
例题精讲
C
证明:连接OC
∵DE切⊙O于点C
∴OC⊥DE
∴∠OCD=90°
又∵∠COB=2∠A,∠A=32°
∴∠COB=64°
∴∠D=∠OCD-∠COB
=26°
例1:AB是⊙O的直径,点D在AB的延长线上,DE切⊙O于点C,若∠A=32°,求∠D的度数。
方法总结:利用切线的性质解题时,常连接圆心与切点,构造直角三角形,利用直角三角形相关性质解题.
变式训练
∴
1.如图,AB为⊙O的直径,D为AB延长线上一点,DC与⊙O相切于点C,∠DAC=30°,
若⊙O的半径长1cm,则CD=
cm.
O
A
B
D
C
分析:连接OC,则OC⊥DE
又∵∠COB=2∠A=60°
∴∠D=∠OCD-∠COB=30°
∴CD=
OC=
变式训练
O
A
B
C
D
2.如图,AB是⊙O的直径,DC切⊙O于点C,连结CA,CB,如果AB=12cm,
∠ACD=30°,求AC的长和∠B的度数。
证明:连接OC
∵DE切⊙O于点C
∴OC⊥DE
∴∠OCD=90°
又∵∠ACD=30°
∴∠ACO=60°
又∵OA=OC
∴△AOC是等边三角形
∴AB=2AC,∠AOC=60°
∴AC=6cm,∠B=30°
变式训练
3.如图,在☉O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为(
)
A.40°
B.35°
C.30°
D.45°
C
O
A
B
C
D
P
二、圆的切线的判定和性质综合运用
例2:如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.
求证:CD与⊙O相切.
证明:连接OM,过点O作ON⊥CD于点N,
∵⊙O与BC相切于点M,
∴OM⊥BC.
又∵ON⊥CD,
O为正方形ABCD对角线AC上一点,
∴OM=ON,
∴CD与⊙O相切.
M
N
课堂小结
圆的切线的性质
圆的切线垂直于经过切点的半径
性质定理
辅助线作法
见切线,连过切点的半径,得垂直.
1.PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点(不与点A
、B
重合),若∠APB=40°,
求∠ACB的度数.
课堂检测
B
A
O
P
C
证明:连接OA,OB
∵PA、PB切⊙O于A、B
∴∠OAP=∠OBP=90°
又∵∠APB=40°
∴∠AOB=140°
∴∠ACB=70°
课堂检测
2.如图,AB为⊙O的直径,C为⊙O上的一点,AD和过C点的切线互相垂直,垂足为D。求证:AC平分∠DAB
D
A
B
C
O
证明:连接OC
∵CD切⊙O于点C
∴OC⊥CD
又∵AD⊥CD
∴AD∥OC
∴∠CAD=∠OCA
又∵OA=OC
∴∠OAC=∠OCA
∴∠OAC=∠CAD
即:AC平分∠DAB
课堂检测
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作⊙O的切线交AC于点D,试判断△AED的形状,并说明理由.
D
A
B
C
O
E
解:△AED是直角三角形,理由如下:
连接OE
∵AE平分∠BAC
∴∠CAE=∠OAE
又∵OA=OE
∴∠OAE=∠OEA
∴∠OEA=∠CAE
∴AD∥OE
又∵DE切⊙O于点E
∴OE⊥DE
∴AD⊥DE
∴△AED是直角三角形
同课章节目录
