北师大版九年级数学上册第六章反比例函数重点题型归纳学案(Word版,无答案)
文档属性
| 名称 | 北师大版九年级数学上册第六章反比例函数重点题型归纳学案(Word版,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 327.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 12:04:44 | ||
图片预览



文档简介
第六章
反比例函数
【学习目标】
1.会判断一个函数是否是反比例函数.(重点)
2.会求反比例函数的表达式.(难点)
3.掌握反比例函数图象的特征.(重点)
4.会利用反比例函数图象解决相关问题.(难点)
【知识点内容】
知识点一:反比例函数的概念:一般地,如果两个变量y与x的关系可以表示成,的形式,那么称
y
是
x
的反比例函数.
形如、、的函数称为y关于x的反比例函数。
例题1:在下列关系式中,x均为自变量,哪些式反比例函数?每个反比例函数相应的k值是多少?
1.已知是反比例函数,则m=
.
2.已知函数是反比例函数,则k=
.
②确定反比例函数解析式:用待定系数法求反比例函数
例题2:已知反比例函数y=(k≠0)的图象经过点A(﹣3,﹣6).
(1)求这个函数的表达式;
(2)点B(4,),C(2,﹣5)是否在这个函数的图象上?
3.某反比例函数的图象经过点(﹣2,3),则此函数图象也经过点( )
A.(2,﹣3)
B.(﹣3,﹣3)
C.(2,3)
D.(﹣4,6)
4.若反比例函数y=的图象经过点(﹣1,2),则这个函数的图象一定经过点( )
A.(﹣2,﹣1)
B.(﹣,2)
C.(2,﹣1)
D.(,2)
知识点二:反比例函数图像与性质
反比例函数
k的符号
k>0
k<0
图象
性质
①
②函数图象经过一、三象限,在每个现象内,y随x的值增大而减少
①
②函数图象经过二、四象限,在每个现象内,y随x的值增大而增大
反比例函数图象是轴对称图形,也是中心对称图形,关于原点对称
5.关于反比例函数y=图象,下列说法正确的是( )
A.点(﹣2,1)在它的图象上
B.它的图象经过原点
C.它的图象在第一、三象限
D.当x>0时,y随x的增大而增大
6.已知反比例函数y=﹣,下列结论:①图象必经过(﹣2,4);②图象在二,四象限内;③y随x的增大而增大;④当x>﹣1时,则y>8.其中错误的结论有( )个
A.3
B.2
C.1
D.0
7.已知反比例函数,下列说法中正确的是( )
A.该函数的图象分布在第一、三象限
B.点(﹣4,﹣3)在函数图象上
C.y随x的增大而增大
D.若点(﹣2,y1)和(﹣1,y2)在该函数图象上,则y1<y2
②利用反比例函数图像解决比大小问题
例题3:已知点A(﹣2,y1)、B(﹣1,y2)、C(3,y3)都在反比例函数y=的图象上,则( )
A.y1<y2<y3
B.y3<y2<y1
C.y3<y1<y2
D.y2<y1<y3
8.反比例函数y=图象上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y1<y2<y3
B.y2<y1<y3
C.y3<y1<y2
D.y3<y2<y1
9.函数(a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1,y2,y3的大小关系是( )
A.y3<y1<y2
B.y3<y2<y1
C.y1<y2<y3
D.y2<y3<y1
10.若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
A.x1<x2<x3
B.x1<x3<x2
C.x2<x1<x3
D.x2<x3<x1
③通过图像性质求未知数取值范围
例题4.反比例函数y=的图象有一支位于第一象限,则常数a的取值范围是
.
11.在反比例函数的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>1
B.k>0
C.k≥1
D.k<1
12.已知A(﹣1,y1),B(2,y2)两点在双曲线y=上,且
y1>y2,则m的取值范围是( )
A.m<0
B.m>0
C.m>﹣
D.m<﹣
13.已知反比例函数的图象上有两点A(x1,y1)、B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是
.
④通过图像解决一次函数与反比例函数大小问题(找交点分成四部分、谁大谁在上)
例题5.如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2=(k2≠0)的图象交于A,B两点,观察图象,当y1>y2时,x的取值范围是
.
(例题5)
(14题图)
14.如图,已知一次函数y=mx+n与反比例函数的图象交于A(3,1)、B(﹣1,﹣3)两点.观察图象,可知不等式的解集是
.
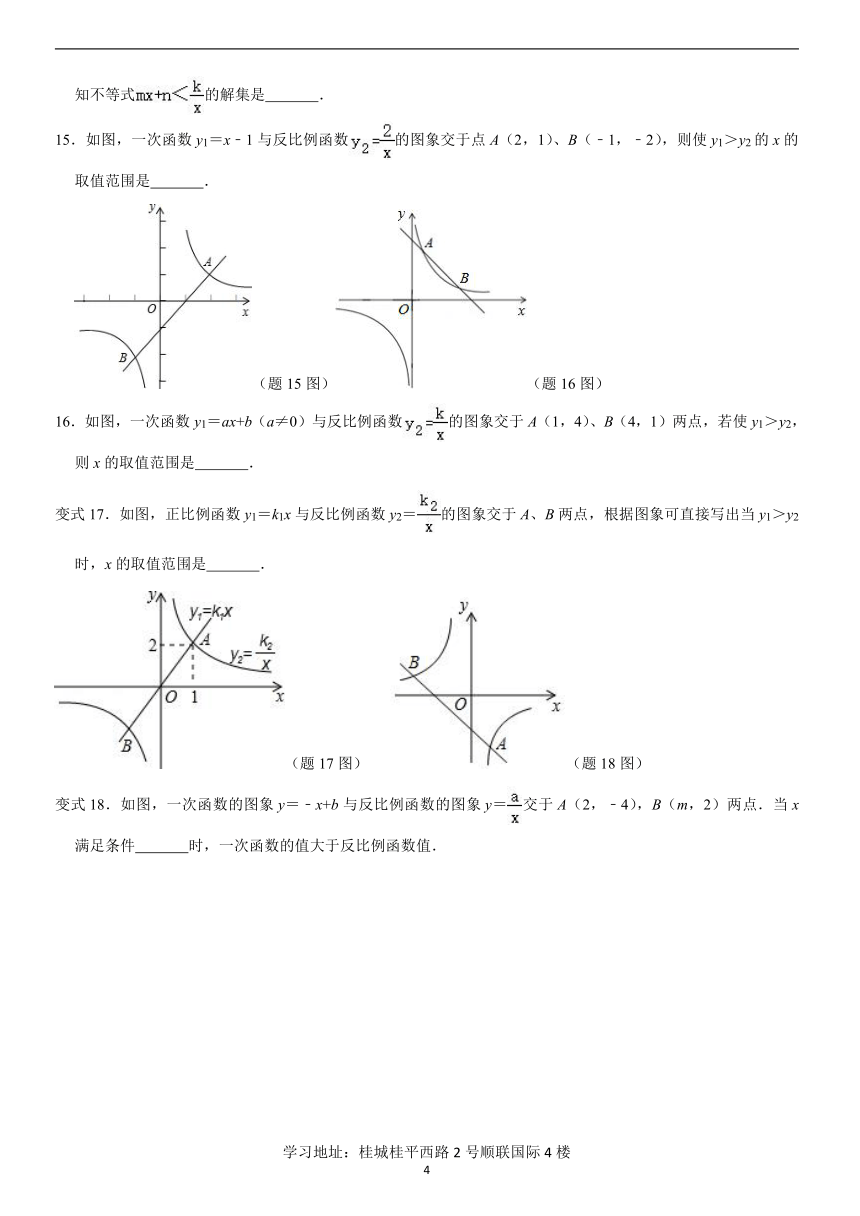
15.如图,一次函数y1=x﹣1与反比例函数的图象交于点A(2,1)、B(﹣1,﹣2),则使y1>y2的x的取值范围是
.
(题15图)(题16图)
16.如图,一次函数y1=ax+b(a≠0)与反比例函数的图象交于A(1,4)、B(4,1)两点,若使y1>y2,则x的取值范围是
.
变式17.如图,正比例函数y1=k1x与反比例函数y2=的图象交于A、B两点,根据图象可直接写出当y1>y2时,x的取值范围是
.
(题17图)
(题18图)
变式18.如图,一次函数的图象y=﹣x+b与反比例函数的图象y=交于A(2,﹣4),B(m,2)两点.当x满足条件
时,一次函数的值大于反比例函数值.
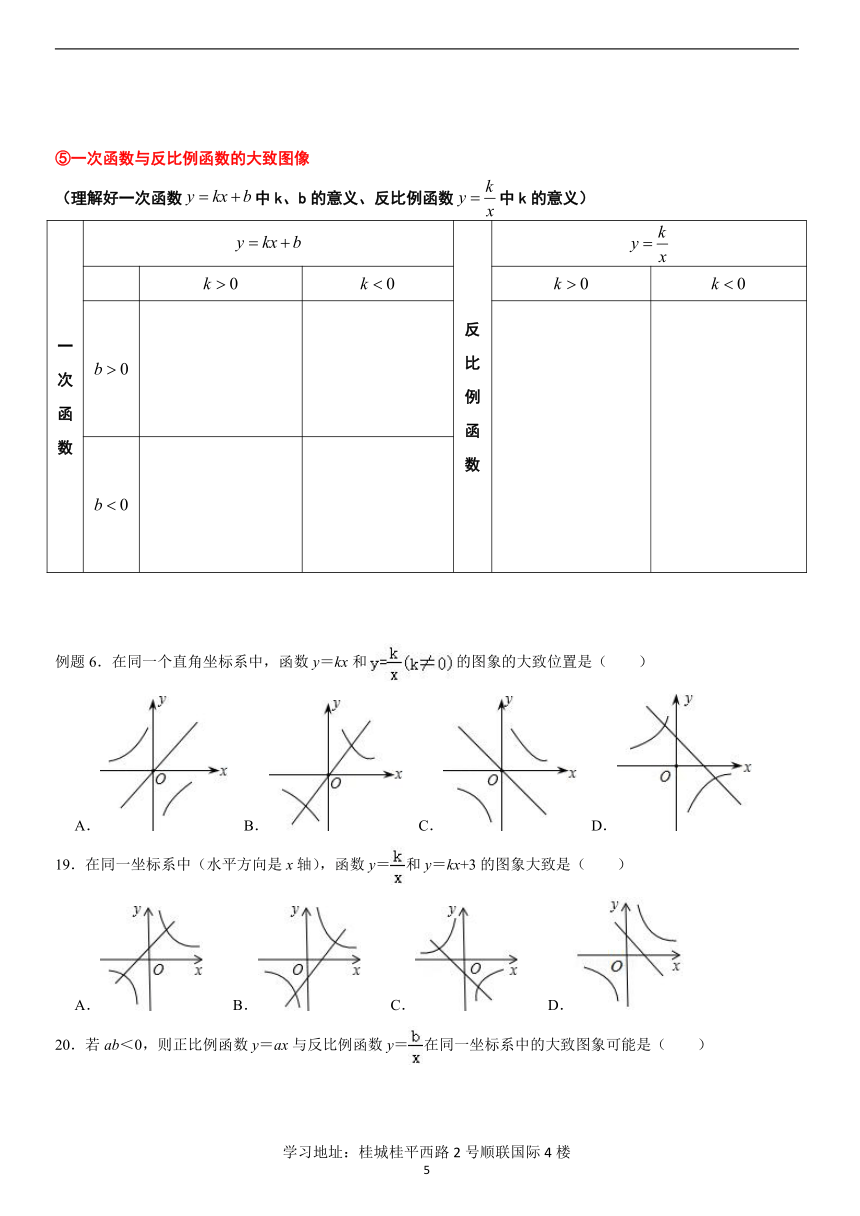
⑤一次函数与反比例函数的大致图像
(理解好一次函数中k、b的意义、反比例函数中k的意义)
一次函数
反比例函数
例题6.在同一个直角坐标系中,函数y=kx和的图象的大致位置是( )
A.
B.
C.
D.
19.在同一坐标系中(水平方向是x轴),函数y=和y=kx+3的图象大致是( )
A.
B.
C.
D.
20.若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的大致图象可能是( )
A.
B.
C.
D.
21.已知k1<0<k2,则函数y=k1x﹣1和y=的图象大致是( )
A.
B.
C.
D.
22.若ab>0,则一次函数y=ax+b与反比例函数y=在同一坐标系中的大致图象是( )
A.
B.
C.
D.
23.已知关于x的函数y=k(x+1)和y=﹣(k≠0),它们在同一坐标系中的大致图象是( )
A.
B.
C.
D.
24.在同一直角坐标系中,函数y=kx﹣k与y=(k≠0)的图象大致是( )
A.
B.
C.
D.
知识点三:反比例函数解析式中k的几何意义
过双曲线()
上任意一点作轴、轴的垂线,所得矩形的面积为.
过双曲线()
上任意一点作一坐标轴的垂线,连接该点和原点,所得三
角形的面积为.
要点诠释:只要函数式已经确定,不论图象上点的位置如何变化,这一点与两坐标轴的垂线和两坐标轴围成的面积始终是不变的.
例题7.如图,点A是反比例函数y=图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足点分别为B、C,矩形ABOC的面积为4,则k=
.
(例题7)(题25图)(题26图)
25.如图,点A是反比例函数y=图象上的一点,AB垂直x轴于点B,若S△ABO=2.5,则k的值为( )
A.2.5
B.5
C.﹣5
D.﹣2.5
26.如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则这个反比例函数的解析式为
.
27.已知反比例函数在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB=
.
(题27图)(题28图)
28.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是
.
29.如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为
.
(题29图)(题30图)
30.如图,点A是反比例函数y=的图象上一点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=的图象于点C,则△OAC的面积为
.
31.双曲线y1、y2在第一象限的图象如图,,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是
.
四:解答题
①相加最小型
1.如图,一次函数y=kx+b与反比例函数y=的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
2.如图,一次函数y1=k1x+b的图象与反比例函数y2=(x>0)的图象交于A、B两点,与y轴交于C点,已知A点坐标为(2,1),C点坐标为(0,3)
(1)求一次函数和反比例函数的解析式;
(2)在x轴上找一点P,使得△PAB的周长最小,请求出点P的坐标.
②求围成面积
3.如图,反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
4.如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)直接写出一次函数的值小于反比例函数值的x的取值范围.
③已知面积反推点坐标
5.如图,一次函数y=kx+b与反比例函数y=的图象交于点A(1,6),B(3,n)两点.与x轴交于点
C.
(1)求一次函数的表达式;
(2)若点M在x轴上,且△AMC的面积为6,求点M的坐标.
(3)结合图形,直接写出kx+b﹣>0时x的取值范围.
(4)在y轴上找一点P,使PA+PB的值最小,直接写出满足条件的点P的坐标是
.
6.如图,矩形ABOD的顶点A是函数y=与函数y=﹣x﹣(k+1)在第二象限的交点,AB⊥x轴于B,AD⊥y轴于D,且矩形ABOD的面积为3.
(1)求两函数的解析式.
(2)求两函数的交点A、C的坐标.
(3)若点P是y轴上一动点,且S△APC=5,求点P的坐标.
7.如图,一次函数y=x+4的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求a,k的值及点B的坐标;
(2)若点P在x轴上,且S△ACP=S△BOC,直接写出点P的坐标.
8.如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
(1)根据图象,直接写出满足k1x+b>的x的取值范围;
(2)求这两个函数的表达式;
(3)点P在线段AB上,且S△AOP:S△BOP=1:2,求点P的坐标.
学习地址:桂城桂平西路2号顺联国际4楼
反比例函数
【学习目标】
1.会判断一个函数是否是反比例函数.(重点)
2.会求反比例函数的表达式.(难点)
3.掌握反比例函数图象的特征.(重点)
4.会利用反比例函数图象解决相关问题.(难点)
【知识点内容】
知识点一:反比例函数的概念:一般地,如果两个变量y与x的关系可以表示成,的形式,那么称
y
是
x
的反比例函数.
形如、、的函数称为y关于x的反比例函数。
例题1:在下列关系式中,x均为自变量,哪些式反比例函数?每个反比例函数相应的k值是多少?
1.已知是反比例函数,则m=
.
2.已知函数是反比例函数,则k=
.
②确定反比例函数解析式:用待定系数法求反比例函数
例题2:已知反比例函数y=(k≠0)的图象经过点A(﹣3,﹣6).
(1)求这个函数的表达式;
(2)点B(4,),C(2,﹣5)是否在这个函数的图象上?
3.某反比例函数的图象经过点(﹣2,3),则此函数图象也经过点( )
A.(2,﹣3)
B.(﹣3,﹣3)
C.(2,3)
D.(﹣4,6)
4.若反比例函数y=的图象经过点(﹣1,2),则这个函数的图象一定经过点( )
A.(﹣2,﹣1)
B.(﹣,2)
C.(2,﹣1)
D.(,2)
知识点二:反比例函数图像与性质
反比例函数
k的符号
k>0
k<0
图象
性质
①
②函数图象经过一、三象限,在每个现象内,y随x的值增大而减少
①
②函数图象经过二、四象限,在每个现象内,y随x的值增大而增大
反比例函数图象是轴对称图形,也是中心对称图形,关于原点对称
5.关于反比例函数y=图象,下列说法正确的是( )
A.点(﹣2,1)在它的图象上
B.它的图象经过原点
C.它的图象在第一、三象限
D.当x>0时,y随x的增大而增大
6.已知反比例函数y=﹣,下列结论:①图象必经过(﹣2,4);②图象在二,四象限内;③y随x的增大而增大;④当x>﹣1时,则y>8.其中错误的结论有( )个
A.3
B.2
C.1
D.0
7.已知反比例函数,下列说法中正确的是( )
A.该函数的图象分布在第一、三象限
B.点(﹣4,﹣3)在函数图象上
C.y随x的增大而增大
D.若点(﹣2,y1)和(﹣1,y2)在该函数图象上,则y1<y2
②利用反比例函数图像解决比大小问题
例题3:已知点A(﹣2,y1)、B(﹣1,y2)、C(3,y3)都在反比例函数y=的图象上,则( )
A.y1<y2<y3
B.y3<y2<y1
C.y3<y1<y2
D.y2<y1<y3
8.反比例函数y=图象上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y1<y2<y3
B.y2<y1<y3
C.y3<y1<y2
D.y3<y2<y1
9.函数(a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1,y2,y3的大小关系是( )
A.y3<y1<y2
B.y3<y2<y1
C.y1<y2<y3
D.y2<y3<y1
10.若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
A.x1<x2<x3
B.x1<x3<x2
C.x2<x1<x3
D.x2<x3<x1
③通过图像性质求未知数取值范围
例题4.反比例函数y=的图象有一支位于第一象限,则常数a的取值范围是
.
11.在反比例函数的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>1
B.k>0
C.k≥1
D.k<1
12.已知A(﹣1,y1),B(2,y2)两点在双曲线y=上,且
y1>y2,则m的取值范围是( )
A.m<0
B.m>0
C.m>﹣
D.m<﹣
13.已知反比例函数的图象上有两点A(x1,y1)、B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是
.
④通过图像解决一次函数与反比例函数大小问题(找交点分成四部分、谁大谁在上)
例题5.如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2=(k2≠0)的图象交于A,B两点,观察图象,当y1>y2时,x的取值范围是
.
(例题5)
(14题图)
14.如图,已知一次函数y=mx+n与反比例函数的图象交于A(3,1)、B(﹣1,﹣3)两点.观察图象,可知不等式的解集是
.
15.如图,一次函数y1=x﹣1与反比例函数的图象交于点A(2,1)、B(﹣1,﹣2),则使y1>y2的x的取值范围是
.
(题15图)(题16图)
16.如图,一次函数y1=ax+b(a≠0)与反比例函数的图象交于A(1,4)、B(4,1)两点,若使y1>y2,则x的取值范围是
.
变式17.如图,正比例函数y1=k1x与反比例函数y2=的图象交于A、B两点,根据图象可直接写出当y1>y2时,x的取值范围是
.
(题17图)
(题18图)
变式18.如图,一次函数的图象y=﹣x+b与反比例函数的图象y=交于A(2,﹣4),B(m,2)两点.当x满足条件
时,一次函数的值大于反比例函数值.
⑤一次函数与反比例函数的大致图像
(理解好一次函数中k、b的意义、反比例函数中k的意义)
一次函数
反比例函数
例题6.在同一个直角坐标系中,函数y=kx和的图象的大致位置是( )
A.
B.
C.
D.
19.在同一坐标系中(水平方向是x轴),函数y=和y=kx+3的图象大致是( )
A.
B.
C.
D.
20.若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的大致图象可能是( )
A.
B.
C.
D.
21.已知k1<0<k2,则函数y=k1x﹣1和y=的图象大致是( )
A.
B.
C.
D.
22.若ab>0,则一次函数y=ax+b与反比例函数y=在同一坐标系中的大致图象是( )
A.
B.
C.
D.
23.已知关于x的函数y=k(x+1)和y=﹣(k≠0),它们在同一坐标系中的大致图象是( )
A.
B.
C.
D.
24.在同一直角坐标系中,函数y=kx﹣k与y=(k≠0)的图象大致是( )
A.
B.
C.
D.
知识点三:反比例函数解析式中k的几何意义
过双曲线()
上任意一点作轴、轴的垂线,所得矩形的面积为.
过双曲线()
上任意一点作一坐标轴的垂线,连接该点和原点,所得三
角形的面积为.
要点诠释:只要函数式已经确定,不论图象上点的位置如何变化,这一点与两坐标轴的垂线和两坐标轴围成的面积始终是不变的.
例题7.如图,点A是反比例函数y=图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足点分别为B、C,矩形ABOC的面积为4,则k=
.
(例题7)(题25图)(题26图)
25.如图,点A是反比例函数y=图象上的一点,AB垂直x轴于点B,若S△ABO=2.5,则k的值为( )
A.2.5
B.5
C.﹣5
D.﹣2.5
26.如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则这个反比例函数的解析式为
.
27.已知反比例函数在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB=
.
(题27图)(题28图)
28.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是
.
29.如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为
.
(题29图)(题30图)
30.如图,点A是反比例函数y=的图象上一点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=的图象于点C,则△OAC的面积为
.
31.双曲线y1、y2在第一象限的图象如图,,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是
.
四:解答题
①相加最小型
1.如图,一次函数y=kx+b与反比例函数y=的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
2.如图,一次函数y1=k1x+b的图象与反比例函数y2=(x>0)的图象交于A、B两点,与y轴交于C点,已知A点坐标为(2,1),C点坐标为(0,3)
(1)求一次函数和反比例函数的解析式;
(2)在x轴上找一点P,使得△PAB的周长最小,请求出点P的坐标.
②求围成面积
3.如图,反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
4.如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)直接写出一次函数的值小于反比例函数值的x的取值范围.
③已知面积反推点坐标
5.如图,一次函数y=kx+b与反比例函数y=的图象交于点A(1,6),B(3,n)两点.与x轴交于点
C.
(1)求一次函数的表达式;
(2)若点M在x轴上,且△AMC的面积为6,求点M的坐标.
(3)结合图形,直接写出kx+b﹣>0时x的取值范围.
(4)在y轴上找一点P,使PA+PB的值最小,直接写出满足条件的点P的坐标是
.
6.如图,矩形ABOD的顶点A是函数y=与函数y=﹣x﹣(k+1)在第二象限的交点,AB⊥x轴于B,AD⊥y轴于D,且矩形ABOD的面积为3.
(1)求两函数的解析式.
(2)求两函数的交点A、C的坐标.
(3)若点P是y轴上一动点,且S△APC=5,求点P的坐标.
7.如图,一次函数y=x+4的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求a,k的值及点B的坐标;
(2)若点P在x轴上,且S△ACP=S△BOC,直接写出点P的坐标.
8.如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
(1)根据图象,直接写出满足k1x+b>的x的取值范围;
(2)求这两个函数的表达式;
(3)点P在线段AB上,且S△AOP:S△BOP=1:2,求点P的坐标.
学习地址:桂城桂平西路2号顺联国际4楼
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
