八年级数学下册课件-17.1 勾股定理-人教版(17张)
文档属性
| 名称 | 八年级数学下册课件-17.1 勾股定理-人教版(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 00:00:00 | ||
图片预览


文档简介
课题:勾股定理的证明
难点名称:数形结合理解勾股定理及证明
*
八年级下册数学-第十七章第1节
目录
CONTENTS
*
B
A
C
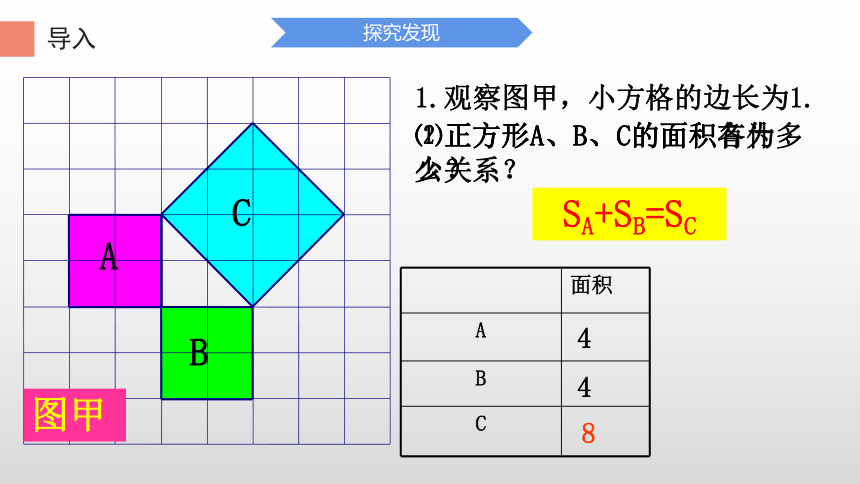
图甲
1.观察图甲,小方格的边长为1.
⑴正方形A、B、C的面积各为多少?
⑵正方形A、B、C的面积有什么关系?
面积
A
B
C
4
4
8
SA+SB=SC
导入
探究发现
课前准备
探究发现
A
B
C
A
B
C
C
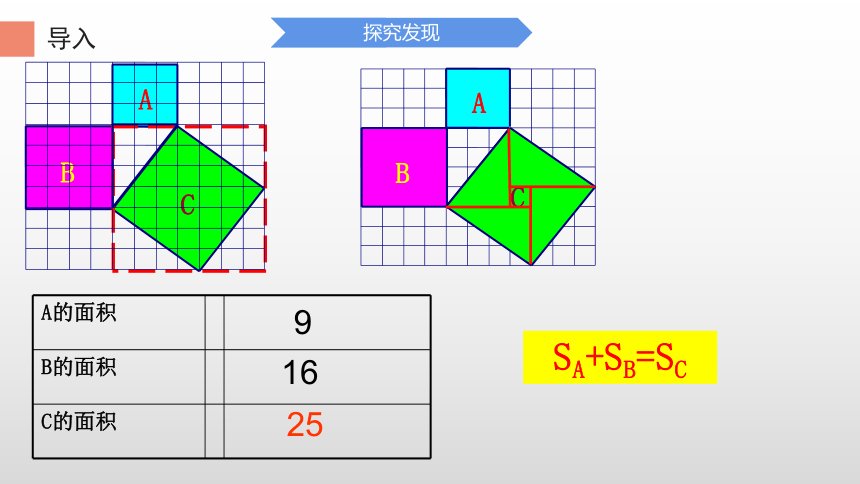
A的面积
B的面积
C的面积
9
16
25
SA+SB=SC
导入
课前准备
探究发现
A
B
C
a
c
b
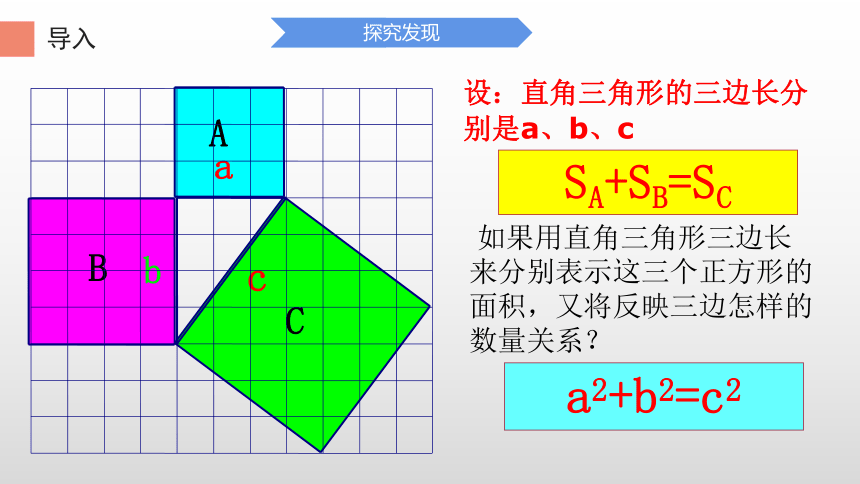
设:直角三角形的三边长分别是a、b、c
SA+SB=SC
如果用直角三角形三边长来分别表示这三个正方形的面积,又将反映三边怎样的数量关系?
a2+b2=c2
导入
课前准备
提出假设
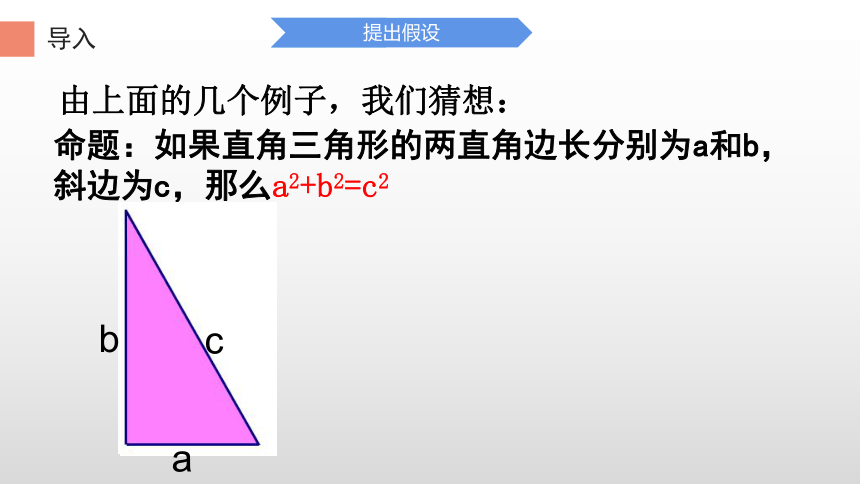
由上面的几个例子,我们猜想:
命题:如果直角三角形的两直角边长分别为a和b,斜边为c,那么a2+b2=c2
a
c
b
导入
课前准备
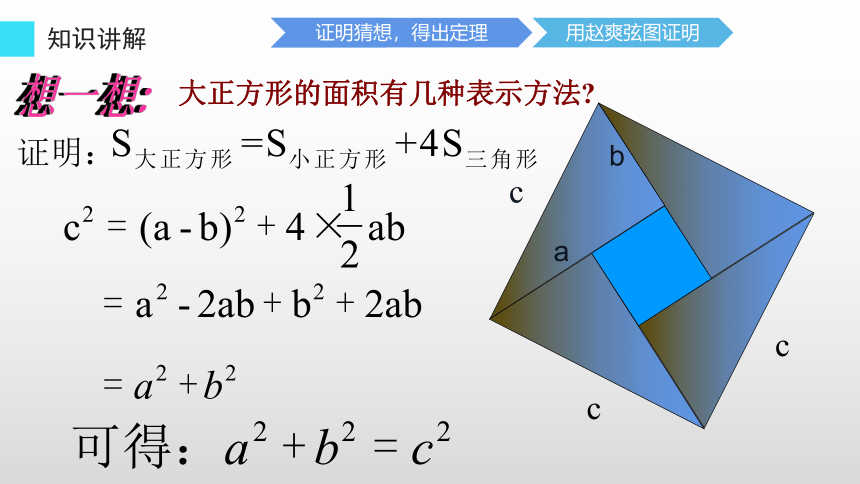
用赵爽弦图证明
证明猜想,得出定理
c
c
a
b
c
a
b
大正方形的面积有几种表示方法?
证明:
知识讲解
课前准备
动手、动画证明
证明猜想,得出定理
你能不能用你手上的4个全等三角形拼成一个正方形?来证明
动画拼图证明
知识讲解
课前准备
动手、动画证明
证明猜想,得出定理
b
a
b
a
c
c
c
c
b
a
b
a
大正方形的面积该怎样表示?
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证明:
知识讲解
课前准备
得出定理
证明猜想,得出定理
定理:经过证明被确认为正确的命题叫做定理。
勾 股 定 理
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
即: 直角三角形两直角边的平方和等于斜边的平方.
知识讲解
1.求出下列直角三角形中未知边的长度
x
3
A
C
B
6
8
x
A
C
B
解:(1)在Rt△ABC中,
由勾股定理得:
X2 =36+64
x2 =100
x2=62+82
∴ x=10
∵x>0
(2)在Rt△ABC中,
由勾股定理:
∴ x=4
x2+32=52
x2=16
x2=52-32
∵x>0
课堂练习
2.在一个直角三角形中, 两边长分别为6、8,则第三边的长为________
10 或
3.如图,受台风莫拉克影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
课堂练习
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系,数形结合更好理解.
⒉勾股定理: 直角三角形两直角边a、b平方和, 等于斜边c平方。
a2+b2 =c2
⒊勾股定理的主要作用是在直角三角形中,已知任意两边求第三边的长。
小结
课前准备
用赵爽弦图证明
证法欣赏,增长见闻
b
a
c
a
b
a
b
c
=
用赵爽弦图证明
课前准备
青朱出入图
证法欣赏,增长见闻
朱方
青方
青入
青入
以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”.
课前准备
茄菲尔德的证法
证法欣赏,增长见闻
b
a
c
b
a
c
c
c
S三角形1 S三角形2 S三角形3
S梯形
化简得:
c2=a2+ b2
=
+
+
(a+b)(a+b)
ab
ab
+
+
c2=
课前准备
证法欣赏,增长见闻
在印度、阿拉伯世界和欧洲出现的一种拼图证明.
难点名称:数形结合理解勾股定理及证明
*
八年级下册数学-第十七章第1节
目录
CONTENTS
*
B
A
C
图甲
1.观察图甲,小方格的边长为1.
⑴正方形A、B、C的面积各为多少?
⑵正方形A、B、C的面积有什么关系?
面积
A
B
C
4
4
8
SA+SB=SC
导入
探究发现
课前准备
探究发现
A
B
C
A
B
C
C
A的面积
B的面积
C的面积
9
16
25
SA+SB=SC
导入
课前准备
探究发现
A
B
C
a
c
b
设:直角三角形的三边长分别是a、b、c
SA+SB=SC
如果用直角三角形三边长来分别表示这三个正方形的面积,又将反映三边怎样的数量关系?
a2+b2=c2
导入
课前准备
提出假设
由上面的几个例子,我们猜想:
命题:如果直角三角形的两直角边长分别为a和b,斜边为c,那么a2+b2=c2
a
c
b
导入
课前准备
用赵爽弦图证明
证明猜想,得出定理
c
c
a
b
c
a
b
大正方形的面积有几种表示方法?
证明:
知识讲解
课前准备
动手、动画证明
证明猜想,得出定理
你能不能用你手上的4个全等三角形拼成一个正方形?来证明
动画拼图证明
知识讲解
课前准备
动手、动画证明
证明猜想,得出定理
b
a
b
a
c
c
c
c
b
a
b
a
大正方形的面积该怎样表示?
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证明:
知识讲解
课前准备
得出定理
证明猜想,得出定理
定理:经过证明被确认为正确的命题叫做定理。
勾 股 定 理
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
即: 直角三角形两直角边的平方和等于斜边的平方.
知识讲解
1.求出下列直角三角形中未知边的长度
x
3
A
C
B
6
8
x
A
C
B
解:(1)在Rt△ABC中,
由勾股定理得:
X2 =36+64
x2 =100
x2=62+82
∴ x=10
∵x>0
(2)在Rt△ABC中,
由勾股定理:
∴ x=4
x2+32=52
x2=16
x2=52-32
∵x>0
课堂练习
2.在一个直角三角形中, 两边长分别为6、8,则第三边的长为________
10 或
3.如图,受台风莫拉克影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
课堂练习
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系,数形结合更好理解.
⒉勾股定理: 直角三角形两直角边a、b平方和, 等于斜边c平方。
a2+b2 =c2
⒊勾股定理的主要作用是在直角三角形中,已知任意两边求第三边的长。
小结
课前准备
用赵爽弦图证明
证法欣赏,增长见闻
b
a
c
a
b
a
b
c
=
用赵爽弦图证明
课前准备
青朱出入图
证法欣赏,增长见闻
朱方
青方
青入
青入
以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”.
课前准备
茄菲尔德的证法
证法欣赏,增长见闻
b
a
c
b
a
c
c
c
S三角形1 S三角形2 S三角形3
S梯形
化简得:
c2=a2+ b2
=
+
+
(a+b)(a+b)
ab
ab
+
+
c2=
课前准备
证法欣赏,增长见闻
在印度、阿拉伯世界和欧洲出现的一种拼图证明.
