八年级数学下册课件-18.1.2 平行四边形的判定(1)-人教版(24张)
文档属性
| 名称 | 八年级数学下册课件-18.1.2 平行四边形的判定(1)-人教版(24张) |  | |
| 格式 | ppt | ||
| 文件大小 | 866.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 19:23:27 | ||
图片预览


文档简介
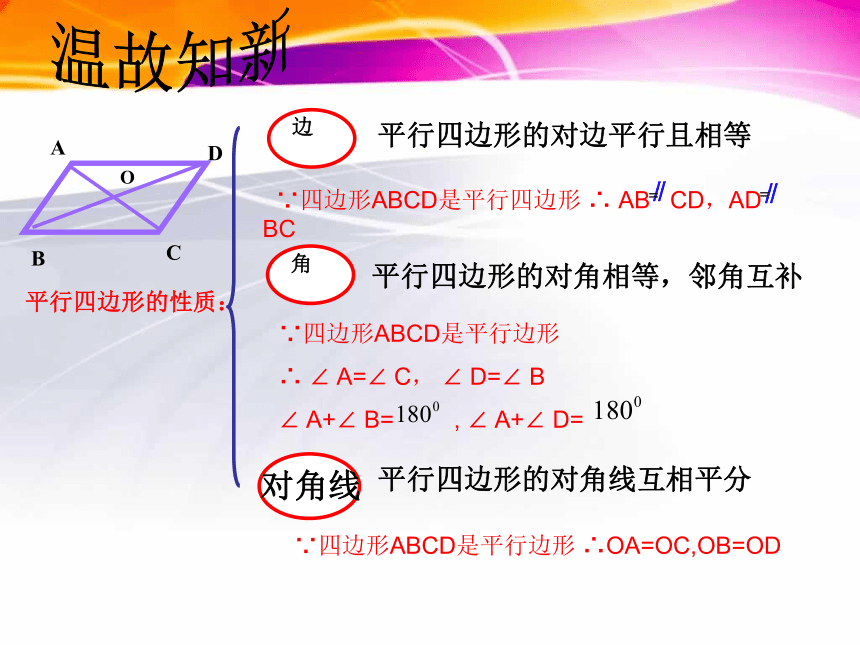
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形 ∴ AB CD,AD BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D=
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD
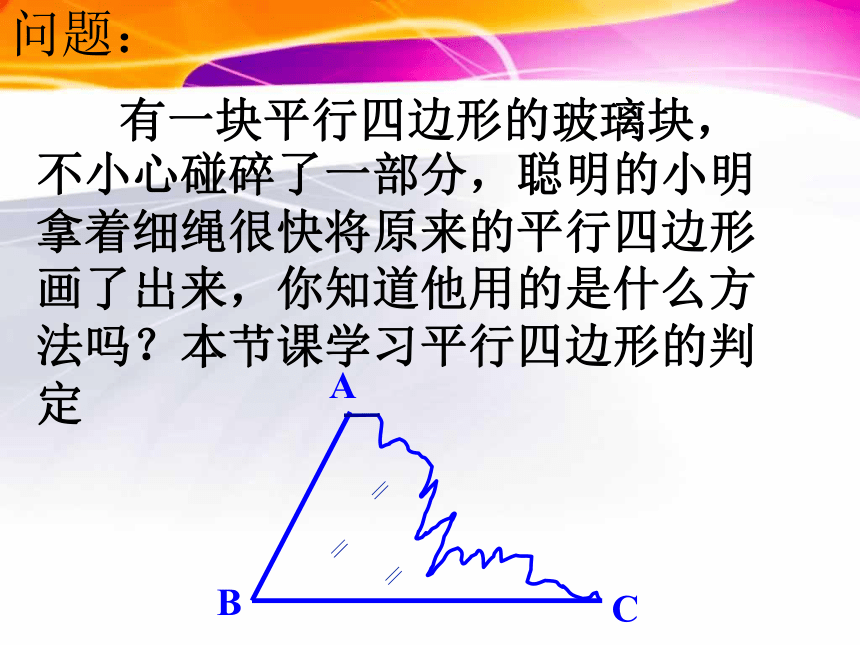
有一块平行四边形的玻璃块,不小心碰碎了一部分,聪明的小明拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么方法吗?本节课学习平行四边形的判定
问题:
A
B
C
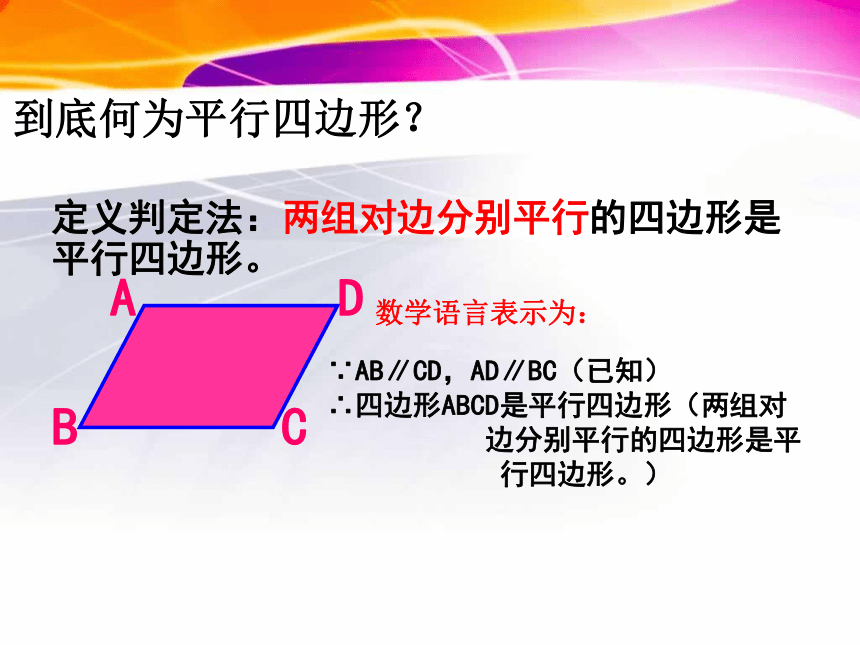
到底何为平行四边形?
定义判定法:两组对边分别平行的四边形是平行四边形。
A
B
C
D
∵AB∥CD,AD∥BC(已知)
∴四边形ABCD是平行四边形(两组对
边分别平行的四边形是平
行四边形。)
数学语言表示为:
从平行四边形的性质逆向思考 提出猜想
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
逆命题
平行四边形的两组对边分别相等
平行四边形的两组对角分别相等
平行四边形的对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:判定这些逆命题的真假?
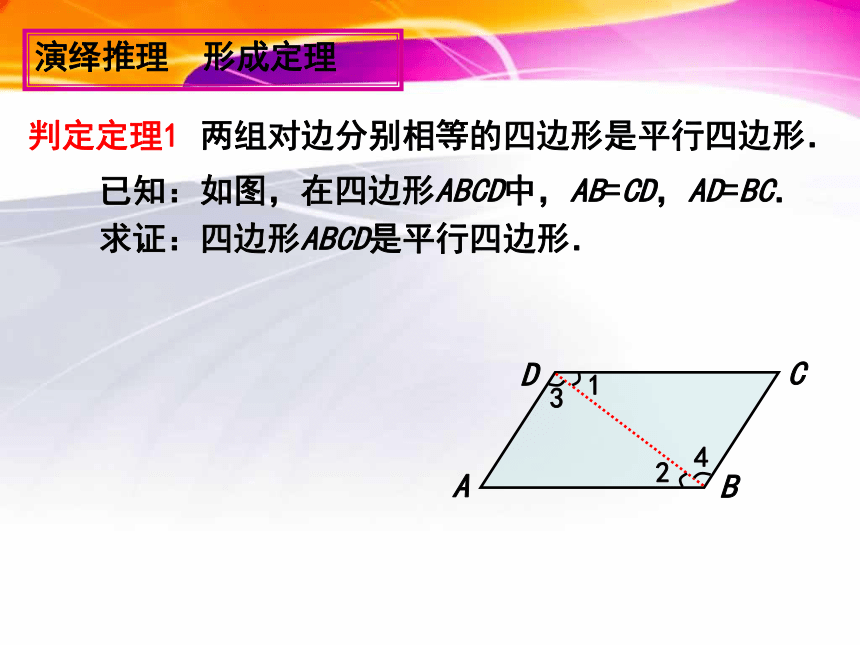
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
演绎推理 形成定理
两组对边分别相等的四边形是平行四边形.
判定定理1
D
A
B
C
1
2
3
4
A
B
C
D
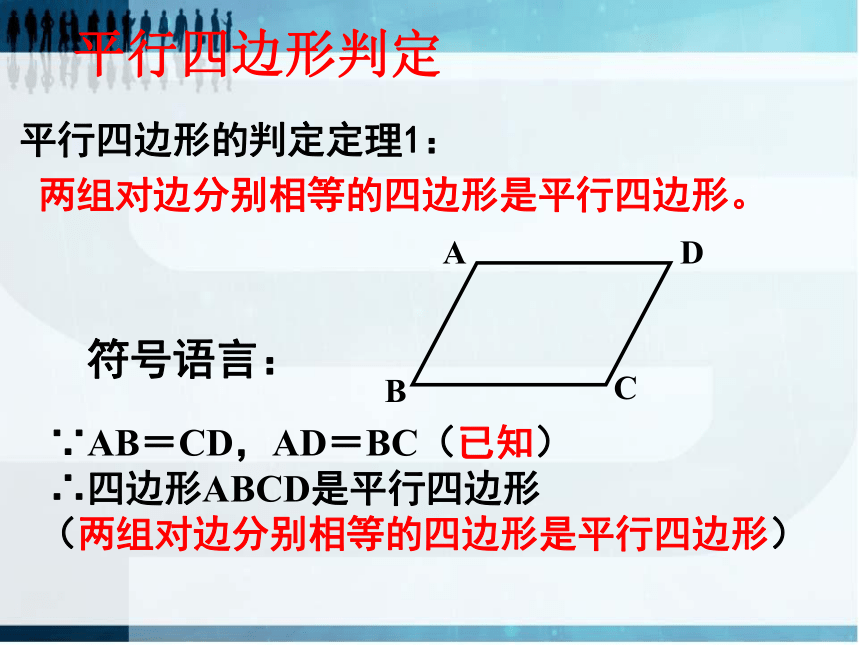
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
平行四边形判定
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
符号语言:
小试牛刀
D
A
B
C
E
F
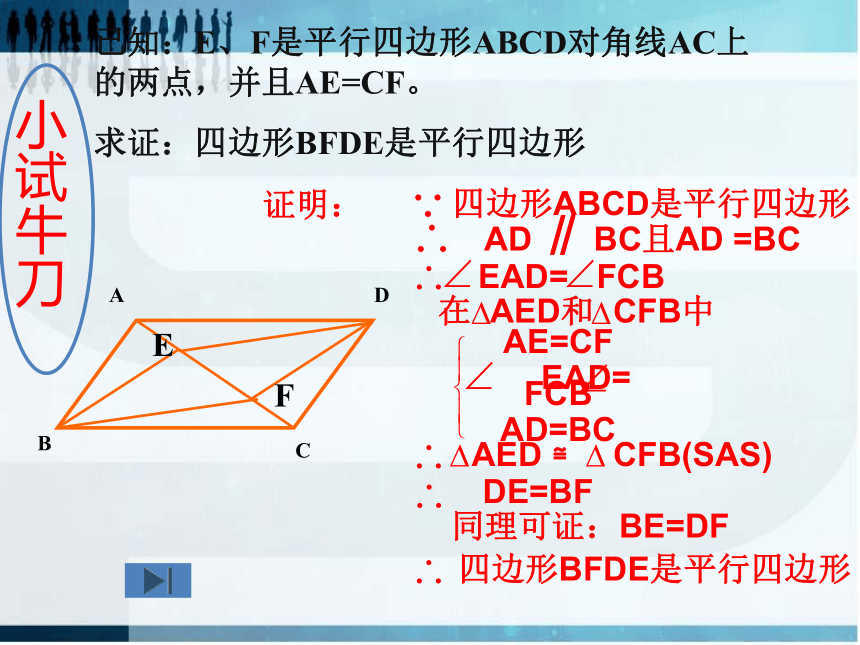
证明:
四边形ABCD是平行四边形
AD ∥ BC且AD =BC
EAD= FCB
AE=CF
EAD= FCB
AD=BC
AED ≌ CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在 AED和 CFB中
同理可证:BE=DF
已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
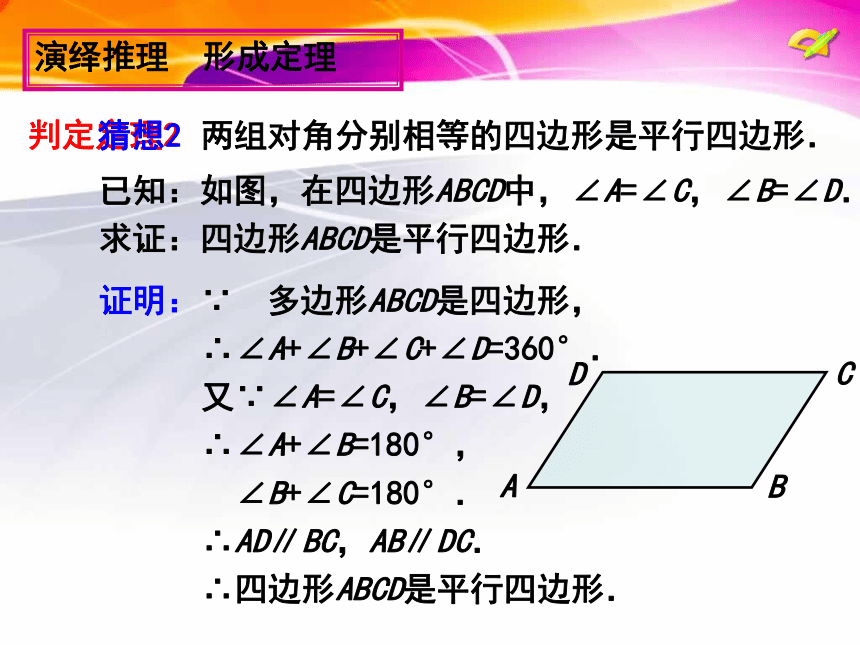
证明:∵ 多边形ABCD是四边形,
∴∠A+∠B+∠C+∠D=360°.
又∵∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
∠B+∠C=180°.
∴AD∥BC,AB∥DC.
∴四边形ABCD是平行四边形.
已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
演绎推理 形成定理
两组对角分别相等的四边形是平行四边形.
判定定理2
猜想2
D
A
B
C
已知:如图,在四边形ABCD中,AC,BD相交于点O, 且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
演绎推理 形成定理
对角线互相平分的四边形是平行四边形.
判定定理3
D
A
B
C
O
猜想3
证明:∵OA=OC,OB=OD,
∠AOD=∠COB,
∴△AOD≌△COB(SAS)
∴∠OAD=∠OCB
∴AD∥BC
同理AB∥DC
∴四边形ABCD是平行四边形.
平行四边形的判定定理:
1.
两组对边分别相等的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
2.
3.
请你识别下列四边形哪些是平行四边形?请说明理由?
A
D
C
B
110°
70°
110°
(1)
(3)
(2)
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
例:已知,平行四边形ABCD对角线AC,BD相较于点O,E、F是AC上的两点,并且E是OA的中点,F是OC的中点.
大显身手
求证:四边形BFDE是平行四边形.
变式1:已知平行四边形ABCD对角线AC,BD相较于点O,E、F是平行四边形ABCD 对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形
改一改,证一证(一)
变式2:已知平行四边形ABCD对角线AC,BD相较于点O, E、F是平行四边形ABCD 对角线AC上的任意两点.
四边形BFDE是平行四边形吗?为什么?
改一改,证一证(二)
同学们现在想想看,你们有没有办法把原来的平行四边形重新画出来?
再回到课前问题1:
A
B
C
D
A
B
C
两组对边分别平行的四边形是平行四边形
D
A
B
C
两组对边分别相等的四边形是平行四边形
D
A
B
C
两组对角分别相等的四边形是平行四边形
D
O
A
B
C
对角线互相平分的四边形是平行四边形
D
C
A
B
平行四边形的判定定理:
O
小结
两组对边分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形。
定义:
两组对边分别平行的四边形是平行四边形
平行四边形的判定方法
P50 习题18.1
第4. 5.13题
作业:
写调查小报告
《生活中平行四边形研究》
F
A
D
B
C
E
1.如图,在 ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,
6
1
2
3
4
7
8
5
求证:四边形AECF是平行四边形。
2.如图,在△ABC中,BD平分∠ABC,DE∥BC交AB于点E,EF∥AC交BC于点F。试判断BE与CF的数量关系,并说明理由。
A
E
D
B
F
C
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形 ∴ AB CD,AD BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D=
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD
有一块平行四边形的玻璃块,不小心碰碎了一部分,聪明的小明拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么方法吗?本节课学习平行四边形的判定
问题:
A
B
C
到底何为平行四边形?
定义判定法:两组对边分别平行的四边形是平行四边形。
A
B
C
D
∵AB∥CD,AD∥BC(已知)
∴四边形ABCD是平行四边形(两组对
边分别平行的四边形是平
行四边形。)
数学语言表示为:
从平行四边形的性质逆向思考 提出猜想
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
逆命题
平行四边形的两组对边分别相等
平行四边形的两组对角分别相等
平行四边形的对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:判定这些逆命题的真假?
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
演绎推理 形成定理
两组对边分别相等的四边形是平行四边形.
判定定理1
D
A
B
C
1
2
3
4
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
平行四边形判定
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
符号语言:
小试牛刀
D
A
B
C
E
F
证明:
四边形ABCD是平行四边形
AD ∥ BC且AD =BC
EAD= FCB
AE=CF
EAD= FCB
AD=BC
AED ≌ CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在 AED和 CFB中
同理可证:BE=DF
已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
证明:∵ 多边形ABCD是四边形,
∴∠A+∠B+∠C+∠D=360°.
又∵∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
∠B+∠C=180°.
∴AD∥BC,AB∥DC.
∴四边形ABCD是平行四边形.
已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
演绎推理 形成定理
两组对角分别相等的四边形是平行四边形.
判定定理2
猜想2
D
A
B
C
已知:如图,在四边形ABCD中,AC,BD相交于点O, 且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
演绎推理 形成定理
对角线互相平分的四边形是平行四边形.
判定定理3
D
A
B
C
O
猜想3
证明:∵OA=OC,OB=OD,
∠AOD=∠COB,
∴△AOD≌△COB(SAS)
∴∠OAD=∠OCB
∴AD∥BC
同理AB∥DC
∴四边形ABCD是平行四边形.
平行四边形的判定定理:
1.
两组对边分别相等的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
2.
3.
请你识别下列四边形哪些是平行四边形?请说明理由?
A
D
C
B
110°
70°
110°
(1)
(3)
(2)
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
例:已知,平行四边形ABCD对角线AC,BD相较于点O,E、F是AC上的两点,并且E是OA的中点,F是OC的中点.
大显身手
求证:四边形BFDE是平行四边形.
变式1:已知平行四边形ABCD对角线AC,BD相较于点O,E、F是平行四边形ABCD 对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形
改一改,证一证(一)
变式2:已知平行四边形ABCD对角线AC,BD相较于点O, E、F是平行四边形ABCD 对角线AC上的任意两点.
四边形BFDE是平行四边形吗?为什么?
改一改,证一证(二)
同学们现在想想看,你们有没有办法把原来的平行四边形重新画出来?
再回到课前问题1:
A
B
C
D
A
B
C
两组对边分别平行的四边形是平行四边形
D
A
B
C
两组对边分别相等的四边形是平行四边形
D
A
B
C
两组对角分别相等的四边形是平行四边形
D
O
A
B
C
对角线互相平分的四边形是平行四边形
D
C
A
B
平行四边形的判定定理:
O
小结
两组对边分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形。
定义:
两组对边分别平行的四边形是平行四边形
平行四边形的判定方法
P50 习题18.1
第4. 5.13题
作业:
写调查小报告
《生活中平行四边形研究》
F
A
D
B
C
E
1.如图,在 ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,
6
1
2
3
4
7
8
5
求证:四边形AECF是平行四边形。
2.如图,在△ABC中,BD平分∠ABC,DE∥BC交AB于点E,EF∥AC交BC于点F。试判断BE与CF的数量关系,并说明理由。
A
E
D
B
F
C
