八年级数学下册课件-18.2.1 矩形(2)-人教版(21张)
文档属性
| 名称 | 八年级数学下册课件-18.2.1 矩形(2)-人教版(21张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 926.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 00:00:00 | ||
图片预览






文档简介
测量…?
木工朋友在制作窗框后,需要检测所制作的窗框是否是矩形,那么他需要测量哪些数据,其根据又是什么呢?
18.2.1 矩形 (2)
----矩形的判定
1.矩形的定义:
有一个角是直角的平行四边形是矩形。
你还有其它的判定方法吗?
ABCD
∠A=900
ABCD是矩形
二、活动探究
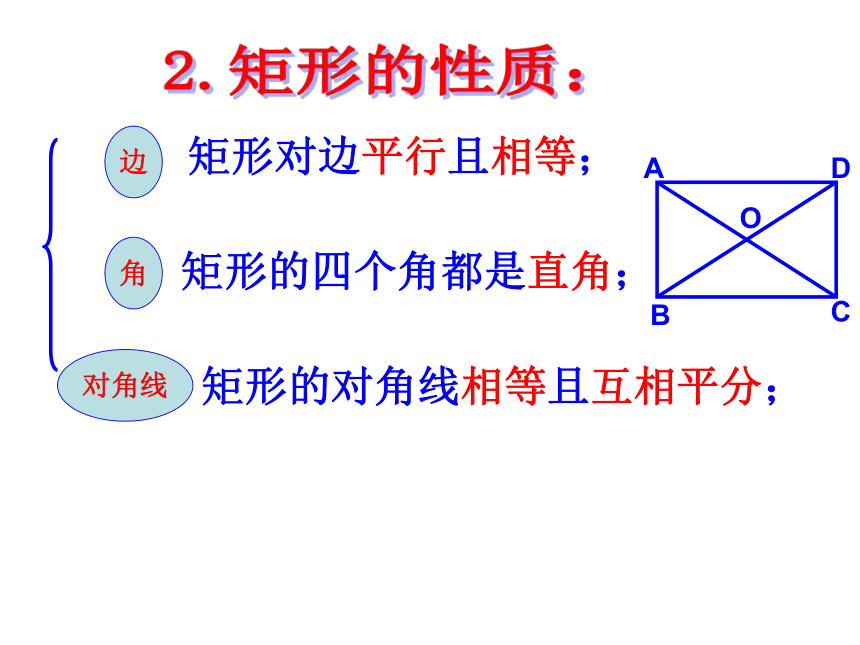
边
对角线
角
A
B
C
D
O
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分;
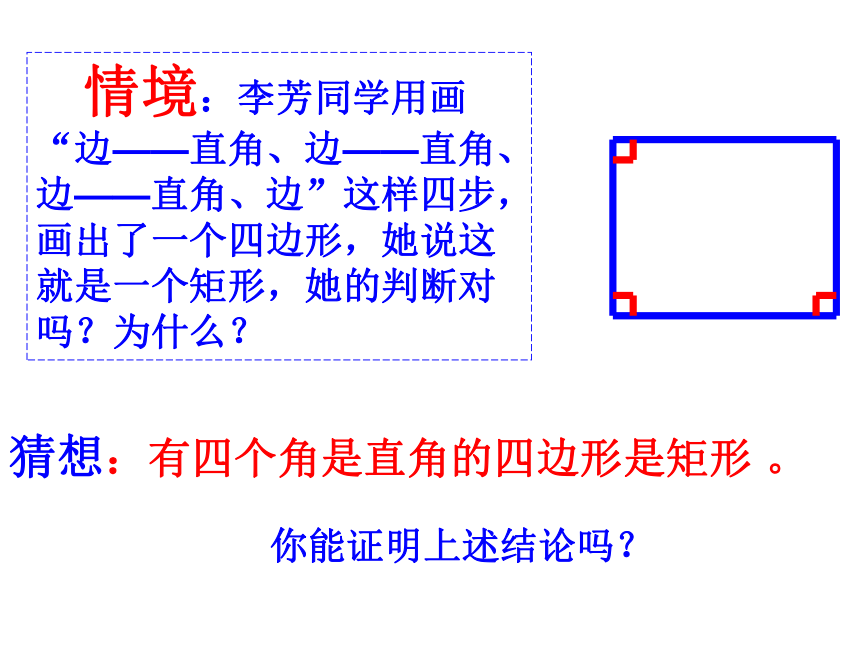
情境:李芳同学用画“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有四个角是直角的四边形是矩形 。
你能证明上述结论吗?
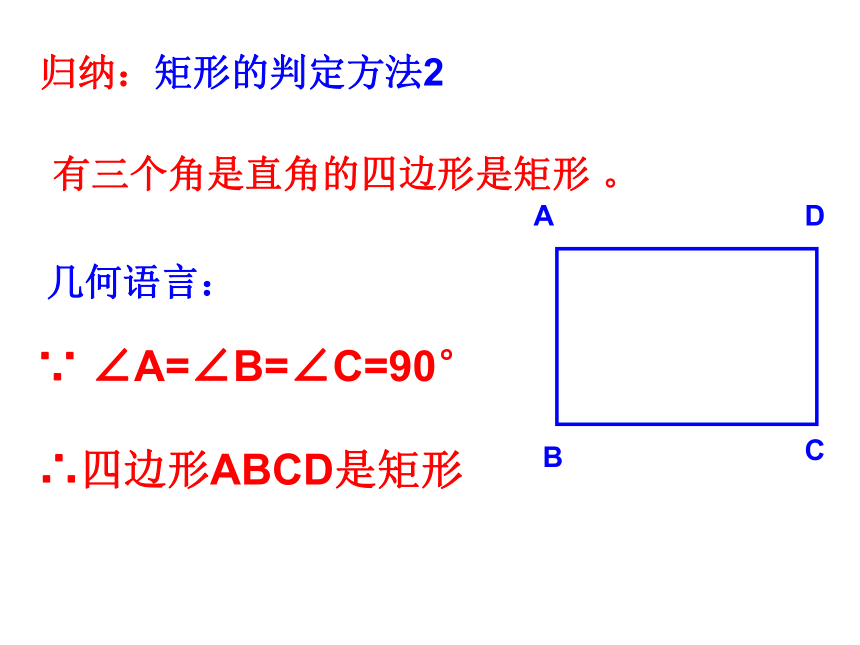
归纳:矩形的判定方法2
有三个角是直角的四边形是矩形 。
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
情境:如果工人师傅已经量得窗框的两组对边相等,接着量一量这个窗框的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形 。
命题:对角线相等的平行四边形是矩形。
已知:平行四边形ABCD中,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
对角线相等的平行四边形是矩形 。
归纳:矩形的判定方法3
几何语言:
∵四边形ABCD是平行四边形
且AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形。)
A
B
C
D
O
(或OA=OC=OB=OD)
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
(对角线相等且互相平分的四边形是矩形)
有三个角是直角的四边形是矩形
方法1:
方法2:
方法3:
三、辨析提升:下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(4)有三个角是直角的四边形是矩形;
(5)四个角都相等的四边形是矩形;
测量…?
现在你可以帮助木工朋友检测所制作的窗框是否是矩形了吧,你可以测量哪些数据,有几种方案,根据又是什么呢?
四、学以致用
例1:如图,M为平行四边形ABCD边AD的
中点,且MB=MC,
求证:四边形ABCD是矩形。
A
B
C
D
M
用全等,
证直角
练习1、如图,平行四边形ABCD中,AB= 6,BC= 8,AC= 10 , 四边形ABCD是矩形吗?为什么?
D
B
C
A
用勾股,证直角
例2:已知:如图,AC与BD相交于点O,
AB CD ,且∠1=∠2 。
求证:四边形ABCD是矩形
3
巧用对角线
A
O
B
D
C
练习2 、已知如图四边形ABCD中
AO=BO=CO=DO,
试说明四边形ABCD是矩形。
先证平行,再证矩形
四个角都是直角的四边形是矩形.
※ 矩形的判定定理2
对角线相等的平行四边形是矩形.
※ 矩形的性质定理3
矩形定义:
有一个角是直角的平行四边形叫做矩形.
六、作业布置:
A组:P55练习2
P67 第4题
B组:P55练习1
P60第3题
七、拓展提高:1.已知:如图,四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD。E、F、G、H分别是AB、
BC、CD、AD的中点。
求证:四边形EFGH是矩形
A
B
C
D
E
F
G
H
O
2、已知: 矩形ABCD的对角线AC、BD相交于O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH。
求证:四边形EFGH是矩形。
木工朋友在制作窗框后,需要检测所制作的窗框是否是矩形,那么他需要测量哪些数据,其根据又是什么呢?
18.2.1 矩形 (2)
----矩形的判定
1.矩形的定义:
有一个角是直角的平行四边形是矩形。
你还有其它的判定方法吗?
ABCD
∠A=900
ABCD是矩形
二、活动探究
边
对角线
角
A
B
C
D
O
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分;
情境:李芳同学用画“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有四个角是直角的四边形是矩形 。
你能证明上述结论吗?
归纳:矩形的判定方法2
有三个角是直角的四边形是矩形 。
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
情境:如果工人师傅已经量得窗框的两组对边相等,接着量一量这个窗框的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形 。
命题:对角线相等的平行四边形是矩形。
已知:平行四边形ABCD中,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
对角线相等的平行四边形是矩形 。
归纳:矩形的判定方法3
几何语言:
∵四边形ABCD是平行四边形
且AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形。)
A
B
C
D
O
(或OA=OC=OB=OD)
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
(对角线相等且互相平分的四边形是矩形)
有三个角是直角的四边形是矩形
方法1:
方法2:
方法3:
三、辨析提升:下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(4)有三个角是直角的四边形是矩形;
(5)四个角都相等的四边形是矩形;
测量…?
现在你可以帮助木工朋友检测所制作的窗框是否是矩形了吧,你可以测量哪些数据,有几种方案,根据又是什么呢?
四、学以致用
例1:如图,M为平行四边形ABCD边AD的
中点,且MB=MC,
求证:四边形ABCD是矩形。
A
B
C
D
M
用全等,
证直角
练习1、如图,平行四边形ABCD中,AB= 6,BC= 8,AC= 10 , 四边形ABCD是矩形吗?为什么?
D
B
C
A
用勾股,证直角
例2:已知:如图,AC与BD相交于点O,
AB CD ,且∠1=∠2 。
求证:四边形ABCD是矩形
3
巧用对角线
A
O
B
D
C
练习2 、已知如图四边形ABCD中
AO=BO=CO=DO,
试说明四边形ABCD是矩形。
先证平行,再证矩形
四个角都是直角的四边形是矩形.
※ 矩形的判定定理2
对角线相等的平行四边形是矩形.
※ 矩形的性质定理3
矩形定义:
有一个角是直角的平行四边形叫做矩形.
六、作业布置:
A组:P55练习2
P67 第4题
B组:P55练习1
P60第3题
七、拓展提高:1.已知:如图,四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD。E、F、G、H分别是AB、
BC、CD、AD的中点。
求证:四边形EFGH是矩形
A
B
C
D
E
F
G
H
O
2、已知: 矩形ABCD的对角线AC、BD相交于O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH。
求证:四边形EFGH是矩形。
