八年级数学下册课件-18.2.2 菱形-人教版(16张)
文档属性
| 名称 | 八年级数学下册课件-18.2.2 菱形-人教版(16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 823.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 19:30:10 | ||
图片预览


文档简介
菱 形
18.2.2特殊的平行四边形
人教版八年级下册数学
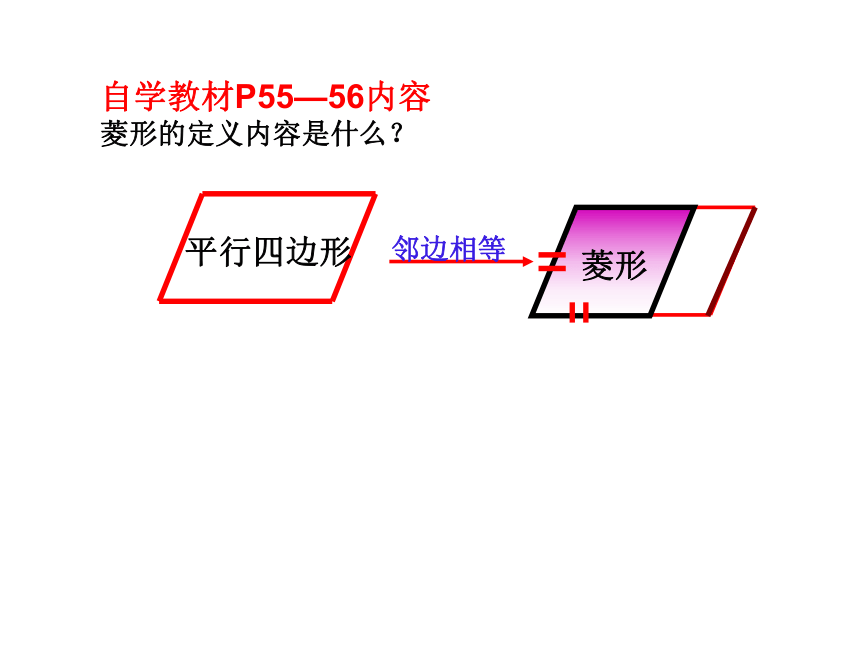
平行四边形
菱形
邻边相等
自学教材P55—56内容
菱形的定义内容是什么?
感受生活
你能举出生活中你看到的菱形吗?
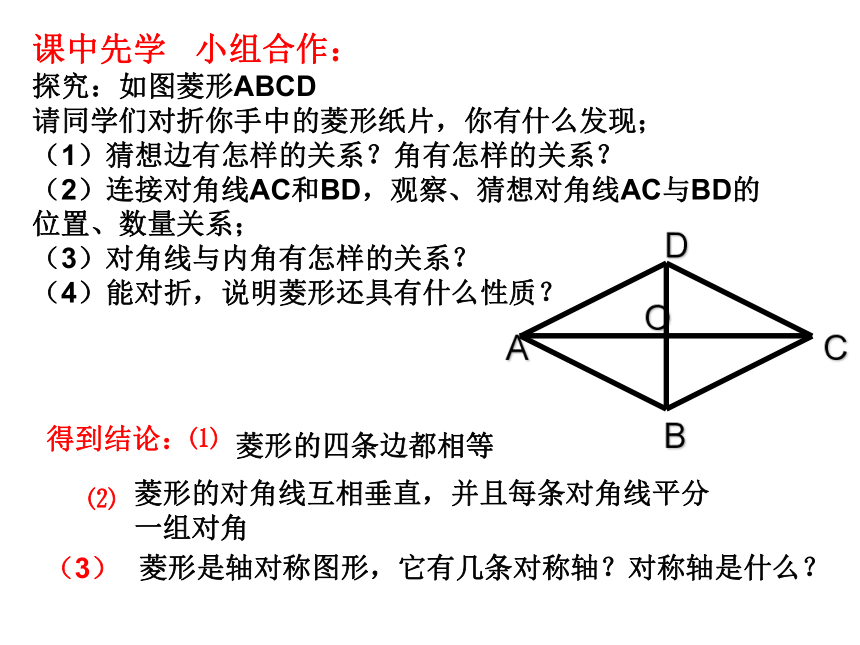
课中先学 小组合作:
探究:如图菱形ABCD
请同学们对折你手中的菱形纸片,你有什么发现;
(1)猜想边有怎样的关系?角有怎样的关系?
(2)连接对角线AC和BD,观察、猜想对角线AC与BD的位置、数量关系;
(3)对角线与内角有怎样的关系?
(4)能对折,说明菱形还具有什么性质?
A
B
C
D
O
得到结论:⑴
⑵
(3)
菱形的四条边都相等
菱形的对角线互相垂直,并且每条对角线平分一组对角
菱形是轴对称图形,它有几条对称轴?对称轴是什么?
菱形的四条边都相等
菱形的对角线互相垂直,并且每条对角线平分一组对角
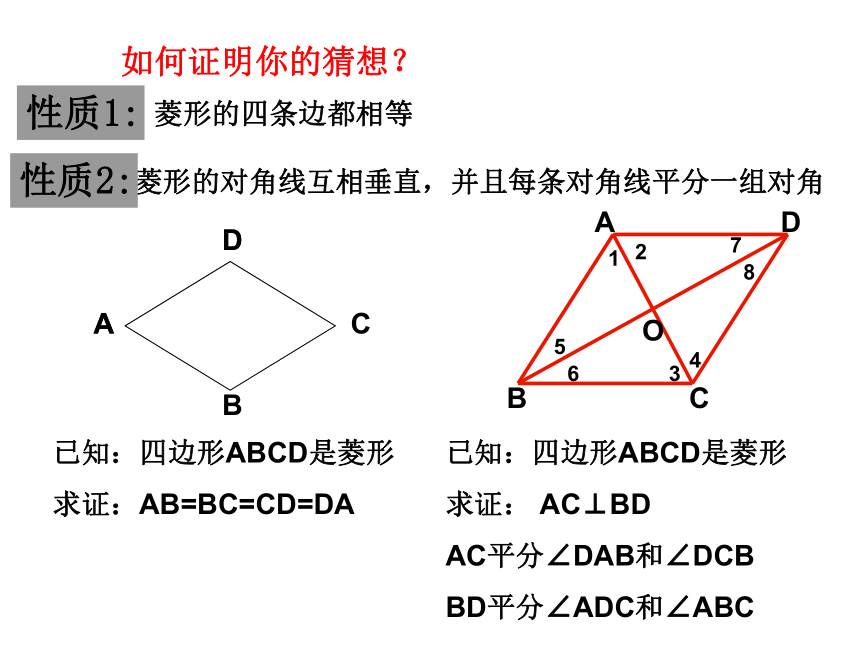
如何证明你的猜想?
A
D
A
B
C
D
O
1
2
3
4
5
6
7
8
已知:四边形ABCD是菱形
求证:AB=BC=CD=DA
性质1:
性质2:
已知:四边形ABCD是菱形
求证: AC⊥BD
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
B
C
A
D
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
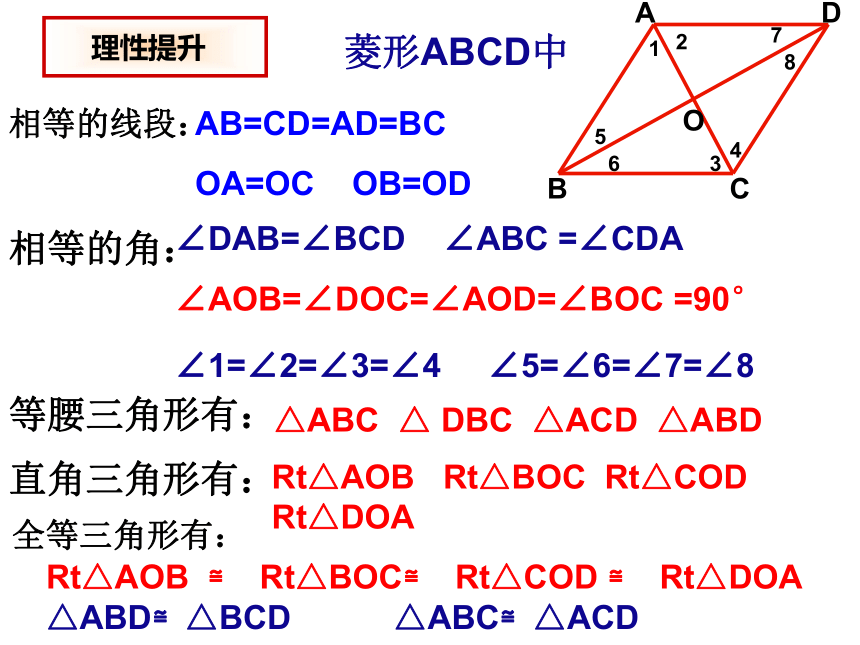
菱形ABCD中
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
理性提升
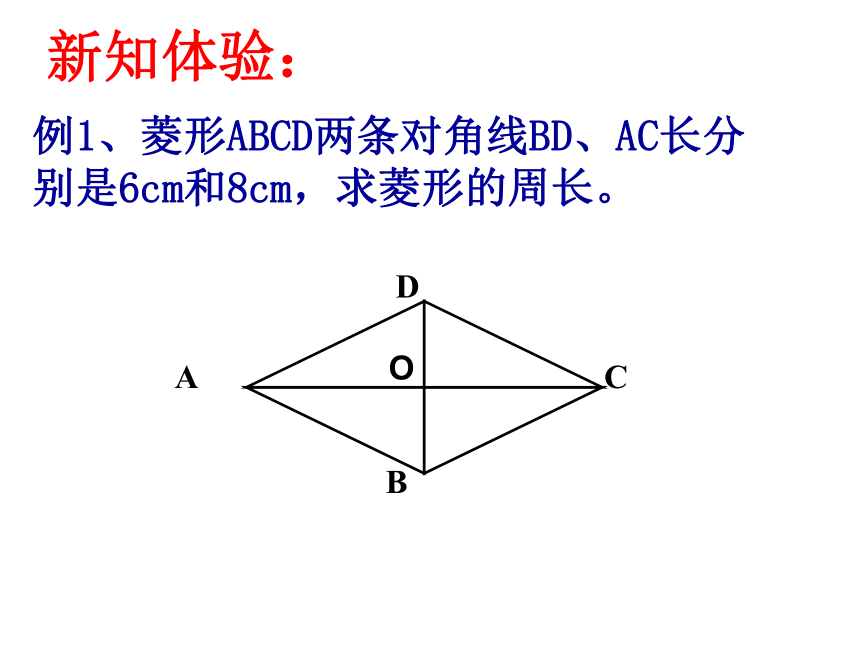
例1、菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长。
C
B
D
A
O
新知体验:
【菱形的面积公式】
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积?
A
B
C
D
O
E
S菱形=BC. AE
思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积吗?
= S△ABD+S△BCD = AC×BD
S菱形ABCD
菱形的面积=底×高=对角线乘积的一半
为 什 么?
课中先学 小组合作:
A
B
C
D
O
E
A
B
C
D
O
E
菱形面积公式的运用
如上图,菱形ABCD两条对角线AC、BD长分别为10cm、24cm,则其周长为 ,高 AE= ,面积为( )
A
B
C
D
O
E
【例1】如图菱形ABCD的周长为40㎝,对角线BD=10㎝.
求①菱形各个角度数.②另一条对角线AC的长. ③菱形的面积
理性提升
利用周长求出的边长恰好等于对角线BD的长.从而得出△ABD是等边三角形,再将AC折半后转化在直角三角形中进行计算,进而求解.
方法构想
A
D
C
B
O
例2、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积。
B
A
O
C
学以致用
1. 如图,在菱形ABCD中,不一定成立的( )
A.四边形ABCD是平行四边形
B.AC⊥BD
C.△ABD是等边三角形
D.∠CAB=∠CAD
A
B
C
D
C
2.已知菱形的周长是12,那么它的边长是( ).
3
3.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。
方法提炼:有关菱形问题可转化为直角三角形或等腰三角形或等边三角形的问题来解决
学以致用
4.菱形的两邻角之比为1:2,如果它的较短对角
线为3cm,则它的周长为( ).
A.8cm B.9cm C.12cm D.15cm
这
堂
课
你
学
到
了
什
么?
回味无穷
从定义上来谈——
有一组邻边相等的平行四边形是 菱形.
从性质上来谈——
①菱形具有平行四边形的一切性质;
②菱形的四边都相等;
③菱形的对角线互相垂直平分,并且每条对角线平分一组对角。
从计算上来谈——
菱形的面积等于它的对角线长的乘积的一半。设菱形的两对角线长分别为a,b,则它的面积S=
ab.
18.2.2特殊的平行四边形
人教版八年级下册数学
平行四边形
菱形
邻边相等
自学教材P55—56内容
菱形的定义内容是什么?
感受生活
你能举出生活中你看到的菱形吗?
课中先学 小组合作:
探究:如图菱形ABCD
请同学们对折你手中的菱形纸片,你有什么发现;
(1)猜想边有怎样的关系?角有怎样的关系?
(2)连接对角线AC和BD,观察、猜想对角线AC与BD的位置、数量关系;
(3)对角线与内角有怎样的关系?
(4)能对折,说明菱形还具有什么性质?
A
B
C
D
O
得到结论:⑴
⑵
(3)
菱形的四条边都相等
菱形的对角线互相垂直,并且每条对角线平分一组对角
菱形是轴对称图形,它有几条对称轴?对称轴是什么?
菱形的四条边都相等
菱形的对角线互相垂直,并且每条对角线平分一组对角
如何证明你的猜想?
A
D
A
B
C
D
O
1
2
3
4
5
6
7
8
已知:四边形ABCD是菱形
求证:AB=BC=CD=DA
性质1:
性质2:
已知:四边形ABCD是菱形
求证: AC⊥BD
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
B
C
A
D
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
菱形ABCD中
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
理性提升
例1、菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长。
C
B
D
A
O
新知体验:
【菱形的面积公式】
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积?
A
B
C
D
O
E
S菱形=BC. AE
思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积吗?
= S△ABD+S△BCD = AC×BD
S菱形ABCD
菱形的面积=底×高=对角线乘积的一半
为 什 么?
课中先学 小组合作:
A
B
C
D
O
E
A
B
C
D
O
E
菱形面积公式的运用
如上图,菱形ABCD两条对角线AC、BD长分别为10cm、24cm,则其周长为 ,高 AE= ,面积为( )
A
B
C
D
O
E
【例1】如图菱形ABCD的周长为40㎝,对角线BD=10㎝.
求①菱形各个角度数.②另一条对角线AC的长. ③菱形的面积
理性提升
利用周长求出的边长恰好等于对角线BD的长.从而得出△ABD是等边三角形,再将AC折半后转化在直角三角形中进行计算,进而求解.
方法构想
A
D
C
B
O
例2、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积。
B
A
O
C
学以致用
1. 如图,在菱形ABCD中,不一定成立的( )
A.四边形ABCD是平行四边形
B.AC⊥BD
C.△ABD是等边三角形
D.∠CAB=∠CAD
A
B
C
D
C
2.已知菱形的周长是12,那么它的边长是( ).
3
3.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。
方法提炼:有关菱形问题可转化为直角三角形或等腰三角形或等边三角形的问题来解决
学以致用
4.菱形的两邻角之比为1:2,如果它的较短对角
线为3cm,则它的周长为( ).
A.8cm B.9cm C.12cm D.15cm
这
堂
课
你
学
到
了
什
么?
回味无穷
从定义上来谈——
有一组邻边相等的平行四边形是 菱形.
从性质上来谈——
①菱形具有平行四边形的一切性质;
②菱形的四边都相等;
③菱形的对角线互相垂直平分,并且每条对角线平分一组对角。
从计算上来谈——
菱形的面积等于它的对角线长的乘积的一半。设菱形的两对角线长分别为a,b,则它的面积S=
ab.
