阳新一中2020—2021学年度高三一轮复习周测卷(二十七)
文档属性
| 名称 | 阳新一中2020—2021学年度高三一轮复习周测卷(二十七) |  | |
| 格式 | zip | ||
| 文件大小 | 887.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 13:42:22 | ||
图片预览




文档简介
阳新一中2020—2021学年度高三一轮复习周测卷(二十七)
数学·综合测试卷一
一、单项选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A={x|x2-4x+3<0},集合,则A∩B=
A.{x|1<x≤2}
B.{x|2≤x<3}
C.{x|2<x<3}
D.{x|1<x<3}
2.设复数,则|z|=
A.
B.
C.
D.
3.设a为实数,则“”是“”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.研究人员随机调查统计了某地n名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若第三组的人数为200,则第二组的人数是
A.450
B.400
C.350
D.300
5.设a=30.2,b=0.23,c=log0.23,则a,b,c的大小关系是
A.a>b>c
B.b>a>c
C.a>c>b
D.c>a>b
6.若正实数a,b满足5a+4b=ab,则2a+3b的最小值是
A.
B.
C.
D.
7.中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物中的一种,现有十二生肖的吉祥物各一个,甲、乙、丙三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、兔、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学选取的礼物都满意,那么不同的选法有
A.50种
B.60种
C.70种
D.90种
8.设抛物线y2=2x的焦点为F,过点的直线与抛物线相交于A,B两点,与抛物线的准线相交于点C,|BF|=2,则
A.
B.
C.
D.
二、多项选择题(在每小题给出的选项中,有多项符合题目要求)
9.要得到y=cos
2x的图象C1,只要将的图象C2作的变化是
A.将的图象C2向左平移个单位长度
B.将的图象C2向右平移个单位长度
C.先作C2关于x轴对称的图象C3,再将图象C3向右平移个单位长度
D.先作C2关于x轴对称的图象C3,再将图象C3向左平移个单位长度
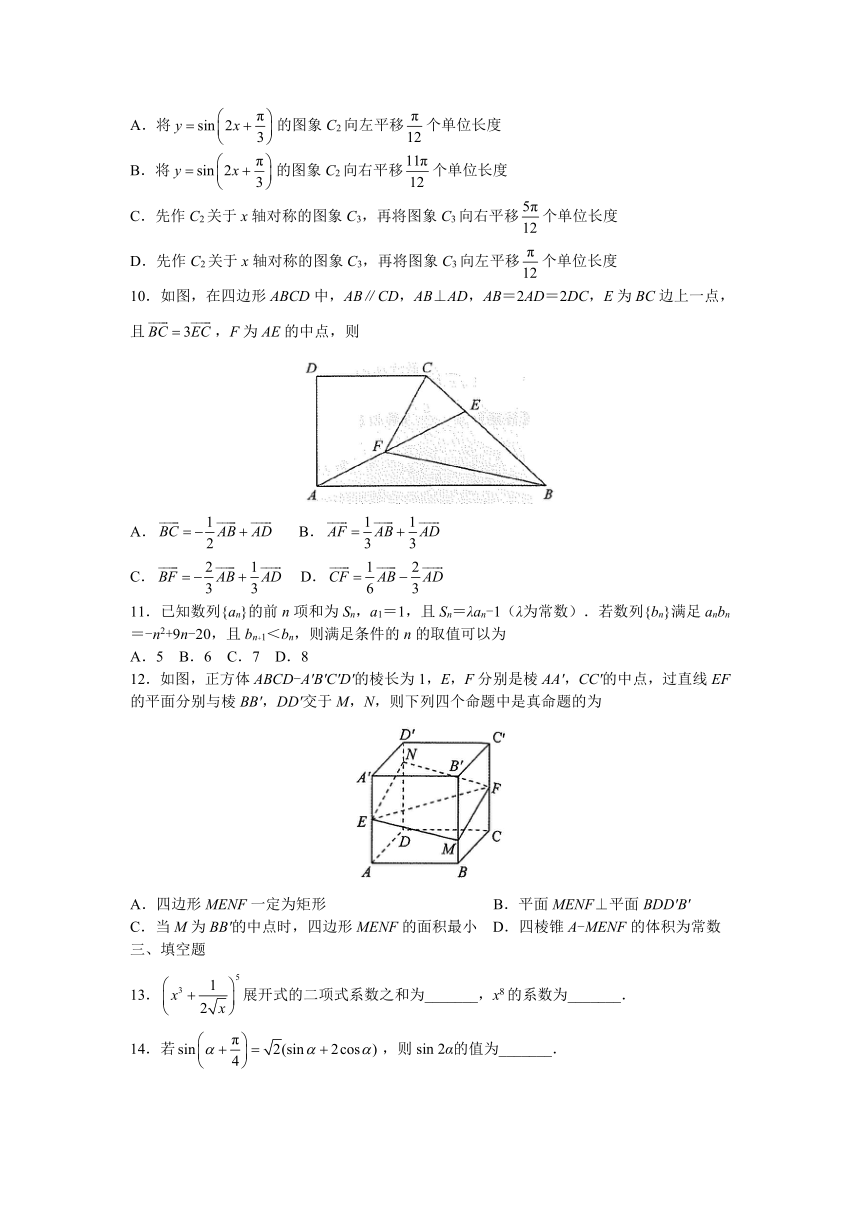
10.如图,在四边形ABCD中,AB∥CD,AB⊥AD,AB=2AD=2DC,E为BC边上一点,且,F为AE的中点,则
A.
B.
C.
D.
11.已知数列{an}的前n项和为Sn,a1=1,且Sn=λan-1(λ为常数).若数列{bn}满足anbn=-n2+9n-20,且bn+1<bn,则满足条件的n的取值可以为
A.5
B.6
C.7
D.8
12.如图,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,则下列四个命题中是真命题的为
A.四边形MENF一定为矩形
B.平面MENF⊥平面BDD′B′
C.当M为BB′的中点时,四边形MENF的面积最小
D.四棱锥A-MENF的体积为常数
三、填空题
13.展开式的二项式系数之和为_______,x8的系数为_______.
14.若,则sin
2α的值为_______.
15.已知双曲线C的中心为坐标原点O,左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于P,Q两点.若PO∥QF2,QA1⊥QA2,则C的离心率为_______.
16.已知f(x)是R上的偶函数,且若关于x的方程2f2(x)-af(x)=0有三个不相等的实数根,则实数a的取值范围是_______.
四、解答题(解答应写出必要的文字说明、证明过程或演算步骤)
17.从①,;②csin
C=sin
A+bsin
B,B=60°;③c=2,这三个条件中任选一个补充在下面问题中,并加以解答.
已知△ABC的内角A,B,C的对边分别为a,b,c,若a=3,_______,求△ABC的面积S.
(注:如果选择多个条件分别作答,则按第一个解答计分)
18.如图,在四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB⊥BC,,E为AD的中点,AC与BE相交于点O.
(1)证明:PO⊥平面ABCD.
(2)求直线BC与平面PBD所成角的正弦值.
19.某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量y(单位:千克)和与它“相近”的株数x具有线性相关关系(两株作物“相近”是指它们的直线距离不超过1(单位:m)),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
x
0
1
2
3
4
y
15
12
11
9
8
(1)求出该种水果每株的产量y关于它“相近”株数x的回归方程.
(2)有一种植户准备种植该种水果500株且每株与它“相近”的株数都为m(m∈N
),计划收获后能全部售出,价格为10元/千克,如果收入(收入=产量×价格)不低于25000元,则m的最大值是多少?
(3)该种植基地在如图所示的直角梯形地块的每个交叉点(直线的交点)处都种了一株该种水果,其中每个小正方形的边长和直角三角形的直角边长都为1
m,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程预测它的产量的分布列与数学期望.
附:回归方程中斜率和截距的最小二乘法估计公式分别为,.
20.已知数列{an}的前n项和为Sn,且满足2Sn=n2-n.
(1)求数列{an}的通项公式;
(2)设(k为正整数),求数列{bn}的前2n项和T2n.
21.已知椭圆C:的左、右焦点分别为F1,F2,离心率为,E为椭圆上一动点(异于左、右顶点),△EF1F2面积的最大值为.
(1)求椭圆C的方程.
(2)若直线l:y=x+m与椭圆C相交于A,B两点,问:y轴上是否存在点M,使得△ABM是以M为直角顶点的等腰直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.
22.已知函数.
(1)若f(x)在区间(-∞,+∞)上是单调递增函数,求a的取值范围.
(2)设g(x)=exf(x),当m≥1时,若g(x1)+g(x2)=2g(m),且x1≠x2,证明:x1+x2<2m.
2020—2021学年度高三一轮复习周测卷(二十七)
数学·综合测试卷一
一、单项选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【解析】
因为集合A={x|x2-4x+3<0}={x|1<x<3},集合,所以A∩B={x|2≤x<3}.故选B.
2.【解析】
因为,所以.故选D.
3.【解析】
由可得,若a=-1,则成立,而不成立,所以应是充分不必要条件.故选A.
4.【解析】
由频率分布直方图可知,则2a=1-(0.24+0.2+0.16),得a=0.20,所以第二组的人数是1000×0.40=400.故选B.
5.【解析】
根据指数函数的性质,可得a=30.2>1,b=0.23∈(0,1),由对数函数的性质,可得c=log0.23<0,所以a>b>c.故选A.
6.【解析】
由5a+4b=ab,得,所以
,当且仅当时取等号.故选C.
7.【解析】
分2种情况讨论:如果甲同学选牛,那么乙同学只能选兔、狗和羊中的一种,丙同学可以从剩下的10种中任意选,所以选法有(种);如果甲同学选马,那么乙同学能选牛、兔、狗和羊中的一种,丙同学可以从剩下的10种中任意选,所以选法有(种),不同的选法共有30+40=70(种).故选C.
8.【解析】
如图,过点A,B分别作准线l:的垂线,垂足分别为A1,B1,因为,又因为△B1BC∽△A1AC,所以.由抛物线定义可得
,由|BF|=|BB1|=2,得,,所以直线AB的方程为
,联立解得yA=2,xA=2,所以.故
.故选A.
二、多项选择题(在每小题给出的选项中,有多项符合题目要求.)
9.【解析】
要得到y=cos
2x的图象C1,只要将的图象C2向左平移个单位长度即可,故A正确;或将的图象C2向右平移个单位长度,故B正确;或先作C2关于x轴对称的图象C3,再将图象C3向右平移个单位长度,故C正确.故选ABC.
10.【解析】
由向量加法的三角形法则,得
,故A正确;因为,所以,所以
,又F为AE的中点,所以,故B正确;所以,故C正确;所以,故D错误.故选ABC.
11.【解析】
因为a1=1,且Sn=λan-1(λ为常数),所以a1=λ-1=1,解得λ=2,所以Sn=2an-1,所以Sn-1=2an-1-1(n≥2),所以an=2an-1,所以an=2n-1.因为anbn=-n2+9n-20,所以,所以,解得4<n<7.又因为n∈N
,所以n=5或n=6.故选AB.
12.【解析】
如图,因为EF⊥BD,EF⊥BB′,BD∩BB′=B,所以EF⊥平面BDD′B′.又因为EF?平面MENF,所以平面MENF⊥平面BDD′B′,故B正确.EF⊥平面BDD′B′,MN?平面BDD′B′,所以EF⊥MN.若MF∥EN,ME∥NF,则四边形MENF为菱形,故A错误.因为菱形MENF的面积为,所以当M为BB′的中点时,四边形MENF的面积最小,故C正确.四棱锥A-MENF的体积为为常数,故D正确.故选BCD.
三、填空题
13.【答案】32
【解析】
由二项式定理,得展开式的二项式系数之和为25=32,展开式的通项为,令,得r=2,故x8的系数为.
14.【答案】【解析】
因为,所以
,整理得tan
α=-3,所以或所以
.
15.【答案】【解析】
已知|A1A2|=2a,QA1⊥QA2,则|OQ|=a,渐近线OQ的斜率为,故.又F2(c,0),PO∥QF2,所以,即,解得a=b,故.
16.【答案】(0,2]∪[3,4]【解析】
由2f2(x)-af(x)=0,得f(x)=0或,因为f(0)=0,f(x)是R上的偶函数,方程f(x)=0或有三个不相等的实数根,所以当x>0时,有唯一一个实数根,如图所示,,所以a∈(0,2]∪[3,4].
四、解答题(解答应写出必要的文字说明、证明过程或演算步骤)
17.解:选择条件①:
因为,,A,C∈(0,π),
所以,,
所以.
由正弦定理,得,
所以
.
选择条件②:
因为csin
C=sin
A+bsin
B,
所以由正弦定理,得c2=a+b2.
因为a=3,所以b2=c2-3.
又因为B=60°,
所以,
所以c=4,
所以.
选择条件③:
因为c=2,,
所以由余弦定理,得,
即,
解得或,b=-2(舍去).
又因为,
所以△ABC的面积.
18.(1)证明:因为AP⊥平面PCD,CD?平面PCD,
所以AP⊥CD.
因为AD∥BC,,
所以四边形BCDE为平行四边形,
所以BE∥CD,所以AP⊥BE.
又因为AB⊥BC,,且E为AD的中点,
所以四边形ABCE为正方形,所以BE⊥AC.
又AP∩AC=A,所以BE⊥平面APC.
因为PO?平面APC,所以BE⊥PO.
因为AP⊥平面PCD,PC?平面PCD,
所以AP⊥PC.
又,
所以△PAC为等腰直角三角形,O为斜边AC上的中点,
所以PO⊥AC,且AC∩BE=O,
所以PO⊥平面ABCD.
(2)解:以O为坐标原点,分别以,,为x,y,z轴的正方向,建立空间直角坐标系O-xyz,如图所示.
设OB=1,则B(1,0,0),C(0,1,0),P(0,0,1),D(-2,1,0),
则,,.
设平面PBD的法向量为
,
则即
令z=1,得.
设直线BC与平面PBD所成角为θ,
则.
19.解:(1)由题意,得,.
,
,
所以.
,
所以.
(2)设每株的产量为y千克,根据题意可得10×500y≥25000,
所以y≥5.
令
,得,即m的最大值是5.
(3)由回归方程可得,当x=1时,,
当x=2时,,当x=3时,,
当x=4时,,
所以,
,
,
.
即的分布列为
P
12.7
11
9.3
7.6
,
即一株产量的数学期望为.
20.解:(1)因为2Sn=n2-n,
所以2Sn-1=(n-1)2-n+1(n≥2),
所以an=Sn-Sn-1=n-1(n≥2),
当n=1时,a1=S1=0,也符合上式,
所以数列{an}是以0为首项,1为公差的等差数列,
故an=n-1.
(2)由(1)知,(k为正整数).
所以
.
21.解:(1)△AF1F2面积的最大值为,则.
又,a2=b2+c2,
解得a2=4,b2=1,
所以椭圆C的方程为.
(2)假设y轴上存在点M(0,t),△ABM是以M为直角顶点的等腰直角三角形,
设A(x1,y1),B(x2,y2),线段AB的中点为N(x0,y0),
由消去y,得5x2+8mx+4m2-4=0,
Δ=64m2-20(4m2-4)=16(5-m2)>0,
解得m2<5,
所以,
,
所以,,
所以,
由题意可知,AM⊥BM,MN⊥l,
由MN⊥l,得,
得,
由AM⊥BM,得
.
又y1=x1+m,y2=x2+m,
可得2x1x2+(m-t)(x1+x2)+(m-t)2=0,
则
,解得m=±1,
当m=1时,点满足题意;当m=-1时,点满足题意,
故y轴上存在点,使得△ABM是以M为直角顶点的等腰直角三角形.
22.(1)解:因为f(x)在区间(-∞,+∞)上是单调递增函数,
所以在R上,恒成立,
即a≥(4-2x)ex,
设h(x)=(4-2x)ex,x∈R,
所以h′(x)=(2-2x)ex,
所以当x∈(-∞,1)时,h′(x)>0,h(x)在区间(-∞,1)上为增函数,
当x∈(1,+∞)时,h′(x)<0,h(x)在区间(1,+∞)上为减函数,
所以h(x)max=h(1)=2e.
因为a≥[(4-2x)ex]max,
所以a≥2e,即a的取值范围为[2e,+∞).
(2)证明:方法一:因为g(x)=ex(x2-4x+5)-a,
所以g′(x)=ex(x-1)2≥0,
所以g(x)在区间(-∞,+∞)上为增函数.
因为g(x1)+g(x2)=2g(m),即g(x1)-g(m)=g(m)-g(x2),
g(x1)-g(m)和g(m)-g(x2)同号,
所以不妨设x1<m<x2,设h(x)=g(2m-x)+g(x)-2g(m)(x>m≥1),
所以φ′(x)=-e2m-x(2m-x-1)2+ex(x-1)2.
因为e2m-x<ex,(2m-x-1)2-(x-1)2=(2m-2)·(2m-2x)≤0,
所以h′(x)>0,所以h(x)在区间(m,+∞)上为增函数,
所以h(x)>h(m)=0,所以h(x2)=g(2m-x2)+g(x2)-2g(m)>0,
所以g(2m-x2)>2g(m)-g(x2)=g(x1),
所以2m-x2>x1,即x1+x2<2m.
方法二:
因为g(x)=exf(x)=(x2-4x+5)ex-a,g(x1)+g(x2)=2g(m),m∈[1,+∞),
所以,
所以
,
所以设φ(x)=(x2-4x+5)ex,x∈R,
则φ(x1)+φ(x2)=2φ(m),
所以φ′(x)=(x-1)2ex≥0,
所以φ(x)在R上单调递增,且φ′(1)=0.
令x1∈(-∞,m),x2∈(m,+∞),
设F(x)=φ(m+x)+φ(m-x),x∈(0,+∞),
所以F′(x)=(m+x-1)2em+x-(m-x-
1)2em-x.
因为x>0,
所以em+x>em-x>0,(m+x-1)2-(m-x-1)2=(2m-2)2x≥0,
所以F′(x)>0,F(x)在区间(0,+∞)上单调递增,
所以F(x)>F(0)=2φ(m),
所以φ(m+x)+φ(m-x)>2φ(m),x∈(0,+∞).
令x=m-x1,
所以φ(m+m-x1)+φ(m-m+x1)>2φ(m),
即φ(2m-x1)+φ(x1)>2φ(m).
又因为φ(x1)+φ(x2)=2φ(m),
所以φ(2m-x1)+2φ(m)-φ(x2)>2φ(m),
即φ(2m-x1)>φ(x2).
因为φ(x)在R上单调递增,
所以2m-x1>x2,即x1+x2<2m得证.
数学·综合测试卷一
一、单项选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A={x|x2-4x+3<0},集合,则A∩B=
A.{x|1<x≤2}
B.{x|2≤x<3}
C.{x|2<x<3}
D.{x|1<x<3}
2.设复数,则|z|=
A.
B.
C.
D.
3.设a为实数,则“”是“”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.研究人员随机调查统计了某地n名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若第三组的人数为200,则第二组的人数是
A.450
B.400
C.350
D.300
5.设a=30.2,b=0.23,c=log0.23,则a,b,c的大小关系是
A.a>b>c
B.b>a>c
C.a>c>b
D.c>a>b
6.若正实数a,b满足5a+4b=ab,则2a+3b的最小值是
A.
B.
C.
D.
7.中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物中的一种,现有十二生肖的吉祥物各一个,甲、乙、丙三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、兔、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学选取的礼物都满意,那么不同的选法有
A.50种
B.60种
C.70种
D.90种
8.设抛物线y2=2x的焦点为F,过点的直线与抛物线相交于A,B两点,与抛物线的准线相交于点C,|BF|=2,则
A.
B.
C.
D.
二、多项选择题(在每小题给出的选项中,有多项符合题目要求)
9.要得到y=cos
2x的图象C1,只要将的图象C2作的变化是
A.将的图象C2向左平移个单位长度
B.将的图象C2向右平移个单位长度
C.先作C2关于x轴对称的图象C3,再将图象C3向右平移个单位长度
D.先作C2关于x轴对称的图象C3,再将图象C3向左平移个单位长度
10.如图,在四边形ABCD中,AB∥CD,AB⊥AD,AB=2AD=2DC,E为BC边上一点,且,F为AE的中点,则
A.
B.
C.
D.
11.已知数列{an}的前n项和为Sn,a1=1,且Sn=λan-1(λ为常数).若数列{bn}满足anbn=-n2+9n-20,且bn+1<bn,则满足条件的n的取值可以为
A.5
B.6
C.7
D.8
12.如图,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,则下列四个命题中是真命题的为
A.四边形MENF一定为矩形
B.平面MENF⊥平面BDD′B′
C.当M为BB′的中点时,四边形MENF的面积最小
D.四棱锥A-MENF的体积为常数
三、填空题
13.展开式的二项式系数之和为_______,x8的系数为_______.
14.若,则sin
2α的值为_______.
15.已知双曲线C的中心为坐标原点O,左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于P,Q两点.若PO∥QF2,QA1⊥QA2,则C的离心率为_______.
16.已知f(x)是R上的偶函数,且若关于x的方程2f2(x)-af(x)=0有三个不相等的实数根,则实数a的取值范围是_______.
四、解答题(解答应写出必要的文字说明、证明过程或演算步骤)
17.从①,;②csin
C=sin
A+bsin
B,B=60°;③c=2,这三个条件中任选一个补充在下面问题中,并加以解答.
已知△ABC的内角A,B,C的对边分别为a,b,c,若a=3,_______,求△ABC的面积S.
(注:如果选择多个条件分别作答,则按第一个解答计分)
18.如图,在四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB⊥BC,,E为AD的中点,AC与BE相交于点O.
(1)证明:PO⊥平面ABCD.
(2)求直线BC与平面PBD所成角的正弦值.
19.某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量y(单位:千克)和与它“相近”的株数x具有线性相关关系(两株作物“相近”是指它们的直线距离不超过1(单位:m)),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
x
0
1
2
3
4
y
15
12
11
9
8
(1)求出该种水果每株的产量y关于它“相近”株数x的回归方程.
(2)有一种植户准备种植该种水果500株且每株与它“相近”的株数都为m(m∈N
),计划收获后能全部售出,价格为10元/千克,如果收入(收入=产量×价格)不低于25000元,则m的最大值是多少?
(3)该种植基地在如图所示的直角梯形地块的每个交叉点(直线的交点)处都种了一株该种水果,其中每个小正方形的边长和直角三角形的直角边长都为1
m,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程预测它的产量的分布列与数学期望.
附:回归方程中斜率和截距的最小二乘法估计公式分别为,.
20.已知数列{an}的前n项和为Sn,且满足2Sn=n2-n.
(1)求数列{an}的通项公式;
(2)设(k为正整数),求数列{bn}的前2n项和T2n.
21.已知椭圆C:的左、右焦点分别为F1,F2,离心率为,E为椭圆上一动点(异于左、右顶点),△EF1F2面积的最大值为.
(1)求椭圆C的方程.
(2)若直线l:y=x+m与椭圆C相交于A,B两点,问:y轴上是否存在点M,使得△ABM是以M为直角顶点的等腰直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.
22.已知函数.
(1)若f(x)在区间(-∞,+∞)上是单调递增函数,求a的取值范围.
(2)设g(x)=exf(x),当m≥1时,若g(x1)+g(x2)=2g(m),且x1≠x2,证明:x1+x2<2m.
2020—2021学年度高三一轮复习周测卷(二十七)
数学·综合测试卷一
一、单项选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【解析】
因为集合A={x|x2-4x+3<0}={x|1<x<3},集合,所以A∩B={x|2≤x<3}.故选B.
2.【解析】
因为,所以.故选D.
3.【解析】
由可得,若a=-1,则成立,而不成立,所以应是充分不必要条件.故选A.
4.【解析】
由频率分布直方图可知,则2a=1-(0.24+0.2+0.16),得a=0.20,所以第二组的人数是1000×0.40=400.故选B.
5.【解析】
根据指数函数的性质,可得a=30.2>1,b=0.23∈(0,1),由对数函数的性质,可得c=log0.23<0,所以a>b>c.故选A.
6.【解析】
由5a+4b=ab,得,所以
,当且仅当时取等号.故选C.
7.【解析】
分2种情况讨论:如果甲同学选牛,那么乙同学只能选兔、狗和羊中的一种,丙同学可以从剩下的10种中任意选,所以选法有(种);如果甲同学选马,那么乙同学能选牛、兔、狗和羊中的一种,丙同学可以从剩下的10种中任意选,所以选法有(种),不同的选法共有30+40=70(种).故选C.
8.【解析】
如图,过点A,B分别作准线l:的垂线,垂足分别为A1,B1,因为,又因为△B1BC∽△A1AC,所以.由抛物线定义可得
,由|BF|=|BB1|=2,得,,所以直线AB的方程为
,联立解得yA=2,xA=2,所以.故
.故选A.
二、多项选择题(在每小题给出的选项中,有多项符合题目要求.)
9.【解析】
要得到y=cos
2x的图象C1,只要将的图象C2向左平移个单位长度即可,故A正确;或将的图象C2向右平移个单位长度,故B正确;或先作C2关于x轴对称的图象C3,再将图象C3向右平移个单位长度,故C正确.故选ABC.
10.【解析】
由向量加法的三角形法则,得
,故A正确;因为,所以,所以
,又F为AE的中点,所以,故B正确;所以,故C正确;所以,故D错误.故选ABC.
11.【解析】
因为a1=1,且Sn=λan-1(λ为常数),所以a1=λ-1=1,解得λ=2,所以Sn=2an-1,所以Sn-1=2an-1-1(n≥2),所以an=2an-1,所以an=2n-1.因为anbn=-n2+9n-20,所以,所以,解得4<n<7.又因为n∈N
,所以n=5或n=6.故选AB.
12.【解析】
如图,因为EF⊥BD,EF⊥BB′,BD∩BB′=B,所以EF⊥平面BDD′B′.又因为EF?平面MENF,所以平面MENF⊥平面BDD′B′,故B正确.EF⊥平面BDD′B′,MN?平面BDD′B′,所以EF⊥MN.若MF∥EN,ME∥NF,则四边形MENF为菱形,故A错误.因为菱形MENF的面积为,所以当M为BB′的中点时,四边形MENF的面积最小,故C正确.四棱锥A-MENF的体积为为常数,故D正确.故选BCD.
三、填空题
13.【答案】32
【解析】
由二项式定理,得展开式的二项式系数之和为25=32,展开式的通项为,令,得r=2,故x8的系数为.
14.【答案】【解析】
因为,所以
,整理得tan
α=-3,所以或所以
.
15.【答案】【解析】
已知|A1A2|=2a,QA1⊥QA2,则|OQ|=a,渐近线OQ的斜率为,故.又F2(c,0),PO∥QF2,所以,即,解得a=b,故.
16.【答案】(0,2]∪[3,4]【解析】
由2f2(x)-af(x)=0,得f(x)=0或,因为f(0)=0,f(x)是R上的偶函数,方程f(x)=0或有三个不相等的实数根,所以当x>0时,有唯一一个实数根,如图所示,,所以a∈(0,2]∪[3,4].
四、解答题(解答应写出必要的文字说明、证明过程或演算步骤)
17.解:选择条件①:
因为,,A,C∈(0,π),
所以,,
所以.
由正弦定理,得,
所以
.
选择条件②:
因为csin
C=sin
A+bsin
B,
所以由正弦定理,得c2=a+b2.
因为a=3,所以b2=c2-3.
又因为B=60°,
所以,
所以c=4,
所以.
选择条件③:
因为c=2,,
所以由余弦定理,得,
即,
解得或,b=-2(舍去).
又因为,
所以△ABC的面积.
18.(1)证明:因为AP⊥平面PCD,CD?平面PCD,
所以AP⊥CD.
因为AD∥BC,,
所以四边形BCDE为平行四边形,
所以BE∥CD,所以AP⊥BE.
又因为AB⊥BC,,且E为AD的中点,
所以四边形ABCE为正方形,所以BE⊥AC.
又AP∩AC=A,所以BE⊥平面APC.
因为PO?平面APC,所以BE⊥PO.
因为AP⊥平面PCD,PC?平面PCD,
所以AP⊥PC.
又,
所以△PAC为等腰直角三角形,O为斜边AC上的中点,
所以PO⊥AC,且AC∩BE=O,
所以PO⊥平面ABCD.
(2)解:以O为坐标原点,分别以,,为x,y,z轴的正方向,建立空间直角坐标系O-xyz,如图所示.
设OB=1,则B(1,0,0),C(0,1,0),P(0,0,1),D(-2,1,0),
则,,.
设平面PBD的法向量为
,
则即
令z=1,得.
设直线BC与平面PBD所成角为θ,
则.
19.解:(1)由题意,得,.
,
,
所以.
,
所以.
(2)设每株的产量为y千克,根据题意可得10×500y≥25000,
所以y≥5.
令
,得,即m的最大值是5.
(3)由回归方程可得,当x=1时,,
当x=2时,,当x=3时,,
当x=4时,,
所以,
,
,
.
即的分布列为
P
12.7
11
9.3
7.6
,
即一株产量的数学期望为.
20.解:(1)因为2Sn=n2-n,
所以2Sn-1=(n-1)2-n+1(n≥2),
所以an=Sn-Sn-1=n-1(n≥2),
当n=1时,a1=S1=0,也符合上式,
所以数列{an}是以0为首项,1为公差的等差数列,
故an=n-1.
(2)由(1)知,(k为正整数).
所以
.
21.解:(1)△AF1F2面积的最大值为,则.
又,a2=b2+c2,
解得a2=4,b2=1,
所以椭圆C的方程为.
(2)假设y轴上存在点M(0,t),△ABM是以M为直角顶点的等腰直角三角形,
设A(x1,y1),B(x2,y2),线段AB的中点为N(x0,y0),
由消去y,得5x2+8mx+4m2-4=0,
Δ=64m2-20(4m2-4)=16(5-m2)>0,
解得m2<5,
所以,
,
所以,,
所以,
由题意可知,AM⊥BM,MN⊥l,
由MN⊥l,得,
得,
由AM⊥BM,得
.
又y1=x1+m,y2=x2+m,
可得2x1x2+(m-t)(x1+x2)+(m-t)2=0,
则
,解得m=±1,
当m=1时,点满足题意;当m=-1时,点满足题意,
故y轴上存在点,使得△ABM是以M为直角顶点的等腰直角三角形.
22.(1)解:因为f(x)在区间(-∞,+∞)上是单调递增函数,
所以在R上,恒成立,
即a≥(4-2x)ex,
设h(x)=(4-2x)ex,x∈R,
所以h′(x)=(2-2x)ex,
所以当x∈(-∞,1)时,h′(x)>0,h(x)在区间(-∞,1)上为增函数,
当x∈(1,+∞)时,h′(x)<0,h(x)在区间(1,+∞)上为减函数,
所以h(x)max=h(1)=2e.
因为a≥[(4-2x)ex]max,
所以a≥2e,即a的取值范围为[2e,+∞).
(2)证明:方法一:因为g(x)=ex(x2-4x+5)-a,
所以g′(x)=ex(x-1)2≥0,
所以g(x)在区间(-∞,+∞)上为增函数.
因为g(x1)+g(x2)=2g(m),即g(x1)-g(m)=g(m)-g(x2),
g(x1)-g(m)和g(m)-g(x2)同号,
所以不妨设x1<m<x2,设h(x)=g(2m-x)+g(x)-2g(m)(x>m≥1),
所以φ′(x)=-e2m-x(2m-x-1)2+ex(x-1)2.
因为e2m-x<ex,(2m-x-1)2-(x-1)2=(2m-2)·(2m-2x)≤0,
所以h′(x)>0,所以h(x)在区间(m,+∞)上为增函数,
所以h(x)>h(m)=0,所以h(x2)=g(2m-x2)+g(x2)-2g(m)>0,
所以g(2m-x2)>2g(m)-g(x2)=g(x1),
所以2m-x2>x1,即x1+x2<2m.
方法二:
因为g(x)=exf(x)=(x2-4x+5)ex-a,g(x1)+g(x2)=2g(m),m∈[1,+∞),
所以,
所以
,
所以设φ(x)=(x2-4x+5)ex,x∈R,
则φ(x1)+φ(x2)=2φ(m),
所以φ′(x)=(x-1)2ex≥0,
所以φ(x)在R上单调递增,且φ′(1)=0.
令x1∈(-∞,m),x2∈(m,+∞),
设F(x)=φ(m+x)+φ(m-x),x∈(0,+∞),
所以F′(x)=(m+x-1)2em+x-(m-x-
1)2em-x.
因为x>0,
所以em+x>em-x>0,(m+x-1)2-(m-x-1)2=(2m-2)2x≥0,
所以F′(x)>0,F(x)在区间(0,+∞)上单调递增,
所以F(x)>F(0)=2φ(m),
所以φ(m+x)+φ(m-x)>2φ(m),x∈(0,+∞).
令x=m-x1,
所以φ(m+m-x1)+φ(m-m+x1)>2φ(m),
即φ(2m-x1)+φ(x1)>2φ(m).
又因为φ(x1)+φ(x2)=2φ(m),
所以φ(2m-x1)+2φ(m)-φ(x2)>2φ(m),
即φ(2m-x1)>φ(x2).
因为φ(x)在R上单调递增,
所以2m-x1>x2,即x1+x2<2m得证.
