八年级数学下册课件-19.2.2 一次函数-人教版(12张)
文档属性
| 名称 | 八年级数学下册课件-19.2.2 一次函数-人教版(12张) |  | |
| 格式 | pptx | ||
| 文件大小 | 792.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 19:43:10 | ||
图片预览

文档简介
一次函数的图象和性质
难点名称:能根据一次函数的图象理解一次函数的性质;灵活运用一次函数的图象与性质解答有关问题
八年级数学-下册-第十九章第二节
目录
CONTENTS
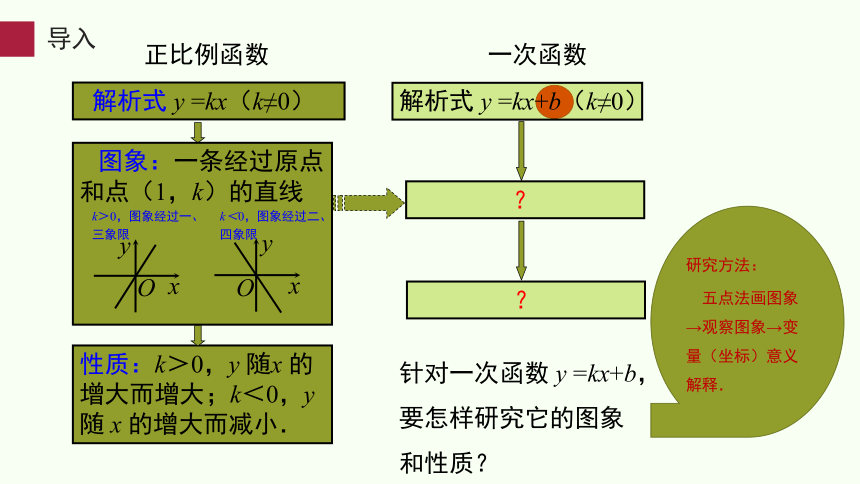
正比例函数
解析式 y =kx(k≠0)
性质:k>0,y 随x 的增大而增大;k<0,y 随 x 的增大而减小.
一次函数
解析式 y =kx+b(k≠0)
针对一次函数 y =kx+b,要怎样研究它的图象和性质?
图象:一条经过原点和点(1,k)的直线
x
y
O
k>0,图象经过一、三象限
k<0,图象经过二、四象限
x
y
O
?
?
导入
研究方法:
五点法画图象→观察图象→变量(坐标)意义解释.
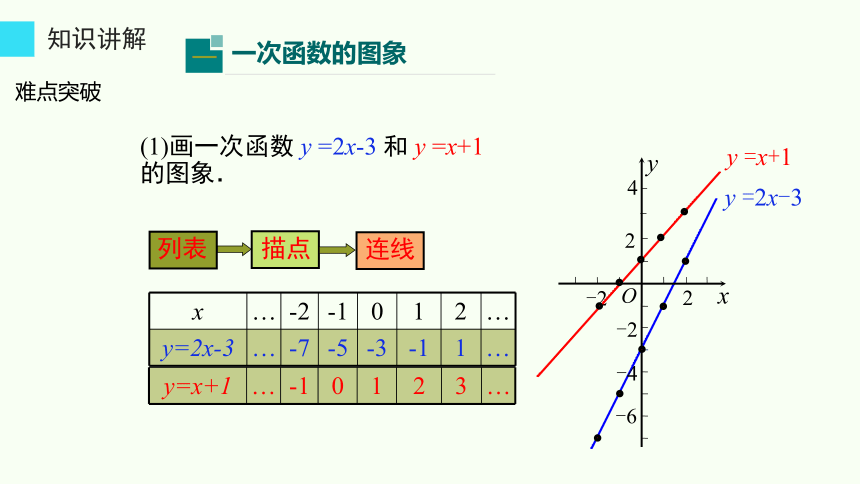
知识讲解
难点突破
一次函数的图象
一
2
-2
-4
-6
-2
2
x
y
O
x
…
-2
-1
0
1
2
…
y=2x-3
…
-7
-5
-3
-1
1
…
描点
连线
列表
(1)画一次函数 y =2x-3 和 y =x+1的图象.
y =2x-3
4
y=x+1
…
-1
0
1
2
3
…
y =x+1
2
-2
-4
-6
-2
2
x
y
0
y =2x-3
4
y =x+1
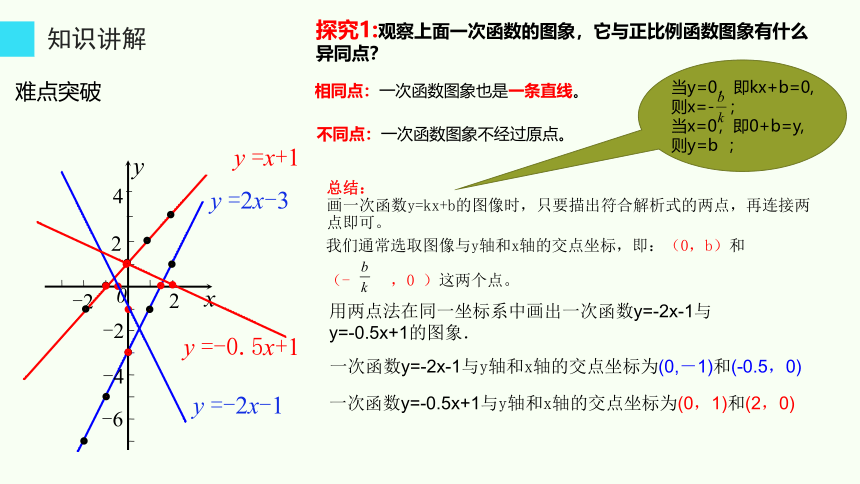
探究1:观察上面一次函数的图象,它与正比例函数图象有什么异同点?
相同点:一次函数图象也是一条直线。
不同点:一次函数图象不经过原点。
总结:
画一次函数y=kx+b的图像时,只要描出符合解析式的两点,再连接两点即可。
用两点法在同一坐标系中画出一次函数y=-2x-1与
y=-0.5x+1的图象.
一次函数y=-2x-1与y轴和x轴的交点坐标为(0,-1)和(-0.5,0)
一次函数y=-0.5x+1与y轴和x轴的交点坐标为(0,1)和(2,0)
y =-2x-1
y =-0.5x+1
知识讲解
难点突破
我们通常选取图像与y轴和x轴的交点坐标,即:(0,b)和
(- ,0 )这两个点。
当y=0,即kx+b=0,则x=- ;
当x=0,即0+b=y,则y=b ;
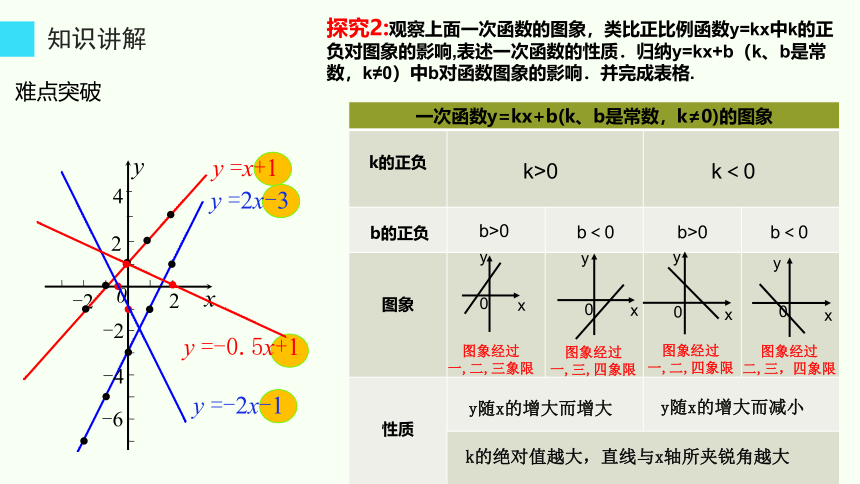
探究2:观察上面一次函数的图象,类比正比例函数y=kx中k的正负对图象的影响,表述一次函数的性质.归纳y=kx+b(k、b是常数,k≠0)中b对函数图象的影响.并完成表格.
2
-2
-4
-6
-2
2
x
y
0
y =2x-3
4
y =x+1
y =-2x-1
y =-0.5x+1
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}一次函数y=kx+b(k、b是常数,k≠0)的图象
k的正负
图象
性质
b>0
b<0
b>0
b<0
x
y
0
图象经过
一,二,三象限
y
x
0
图象经过
一,三,四象限
y随x的增大而增大
x
y
0
图象经过
一,二,四象限
x
y
0
图象经过
二,三,四象限
k>0
k<0
y随x的增大而减小
k的绝对值越大,直线与x轴所夹锐角越大
知识讲解
难点突破
b的正负
课堂练习
难点巩固
1.已知点M(-3, 4)在一次函数y=ax+1的图象上,则a的值是 .
2.直线y=2x-3与x轴交点坐标为 ,与y轴交点坐标为 ,图象经过第__ __ _ 象限,y随x增大而_________.
-1
(3/2,0)
(0,-3)
一、三、四
增大
解析:根据函数图象的定义: 4=-3a+1,所以a=-1.
解析:根据函数定义及坐标轴上点的特点: 求图象与x轴交点,即(-b/k,0);求图象与y轴交点,即(0,b).
4.已知函数y=(m-2)x+n的图象经过一、二、三象限,则m、n的取值范围为 .
3.一次函数y=-x-5的图象不经过____ 象限.
第一
m>2,n>0
课堂练习
难点巩固
解析:根据一次函数图象的特点: k=-1<0,b=-5<0.所以图象经过第二、三、四象限.
解析:根据一次函数图象的特点: 图象经过第一、二、三象限,所以k=m-2>0且b=n>0.解这个不等式组即可.
课堂练习
难点巩固
5.一次函数y=x-2的大致图象为 ( )
y
x
O
A
C
x
O
D
y
x
O
B
y
y
x
O
C
A
6.已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )
y
x
O
A
x
O
D
y
x
O
B
y
y
x
O
C
7.已知P1(x1,y1),P2(x2,y2)是一次函数
y=-0.5x+3图象上的两点,下列判断中,正确的是( )
A.y1>y2 C.当x1<x2时,y1<y2
B.y1<y2 D.当x1<x2时,y1>y2
D
解析:根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.
提示:反过来也成立:y越大,x就越小.
课堂练习
难点巩固
小结
一次函数函数的图象和性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
是一条直线,
与y轴的交点是(0,b),
与x轴的交点是( -b/k,0),
图象
性质
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.
两点法快速画出一次函数图象
谢谢!再见!
难点名称:能根据一次函数的图象理解一次函数的性质;灵活运用一次函数的图象与性质解答有关问题
八年级数学-下册-第十九章第二节
目录
CONTENTS
正比例函数
解析式 y =kx(k≠0)
性质:k>0,y 随x 的增大而增大;k<0,y 随 x 的增大而减小.
一次函数
解析式 y =kx+b(k≠0)
针对一次函数 y =kx+b,要怎样研究它的图象和性质?
图象:一条经过原点和点(1,k)的直线
x
y
O
k>0,图象经过一、三象限
k<0,图象经过二、四象限
x
y
O
?
?
导入
研究方法:
五点法画图象→观察图象→变量(坐标)意义解释.
知识讲解
难点突破
一次函数的图象
一
2
-2
-4
-6
-2
2
x
y
O
x
…
-2
-1
0
1
2
…
y=2x-3
…
-7
-5
-3
-1
1
…
描点
连线
列表
(1)画一次函数 y =2x-3 和 y =x+1的图象.
y =2x-3
4
y=x+1
…
-1
0
1
2
3
…
y =x+1
2
-2
-4
-6
-2
2
x
y
0
y =2x-3
4
y =x+1
探究1:观察上面一次函数的图象,它与正比例函数图象有什么异同点?
相同点:一次函数图象也是一条直线。
不同点:一次函数图象不经过原点。
总结:
画一次函数y=kx+b的图像时,只要描出符合解析式的两点,再连接两点即可。
用两点法在同一坐标系中画出一次函数y=-2x-1与
y=-0.5x+1的图象.
一次函数y=-2x-1与y轴和x轴的交点坐标为(0,-1)和(-0.5,0)
一次函数y=-0.5x+1与y轴和x轴的交点坐标为(0,1)和(2,0)
y =-2x-1
y =-0.5x+1
知识讲解
难点突破
我们通常选取图像与y轴和x轴的交点坐标,即:(0,b)和
(- ,0 )这两个点。
当y=0,即kx+b=0,则x=- ;
当x=0,即0+b=y,则y=b ;
探究2:观察上面一次函数的图象,类比正比例函数y=kx中k的正负对图象的影响,表述一次函数的性质.归纳y=kx+b(k、b是常数,k≠0)中b对函数图象的影响.并完成表格.
2
-2
-4
-6
-2
2
x
y
0
y =2x-3
4
y =x+1
y =-2x-1
y =-0.5x+1
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}一次函数y=kx+b(k、b是常数,k≠0)的图象
k的正负
图象
性质
b>0
b<0
b>0
b<0
x
y
0
图象经过
一,二,三象限
y
x
0
图象经过
一,三,四象限
y随x的增大而增大
x
y
0
图象经过
一,二,四象限
x
y
0
图象经过
二,三,四象限
k>0
k<0
y随x的增大而减小
k的绝对值越大,直线与x轴所夹锐角越大
知识讲解
难点突破
b的正负
课堂练习
难点巩固
1.已知点M(-3, 4)在一次函数y=ax+1的图象上,则a的值是 .
2.直线y=2x-3与x轴交点坐标为 ,与y轴交点坐标为 ,图象经过第__ __ _ 象限,y随x增大而_________.
-1
(3/2,0)
(0,-3)
一、三、四
增大
解析:根据函数图象的定义: 4=-3a+1,所以a=-1.
解析:根据函数定义及坐标轴上点的特点: 求图象与x轴交点,即(-b/k,0);求图象与y轴交点,即(0,b).
4.已知函数y=(m-2)x+n的图象经过一、二、三象限,则m、n的取值范围为 .
3.一次函数y=-x-5的图象不经过____ 象限.
第一
m>2,n>0
课堂练习
难点巩固
解析:根据一次函数图象的特点: k=-1<0,b=-5<0.所以图象经过第二、三、四象限.
解析:根据一次函数图象的特点: 图象经过第一、二、三象限,所以k=m-2>0且b=n>0.解这个不等式组即可.
课堂练习
难点巩固
5.一次函数y=x-2的大致图象为 ( )
y
x
O
A
C
x
O
D
y
x
O
B
y
y
x
O
C
A
6.已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )
y
x
O
A
x
O
D
y
x
O
B
y
y
x
O
C
7.已知P1(x1,y1),P2(x2,y2)是一次函数
y=-0.5x+3图象上的两点,下列判断中,正确的是( )
A.y1>y2 C.当x1<x2时,y1<y2
B.y1<y2 D.当x1<x2时,y1>y2
D
解析:根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.
提示:反过来也成立:y越大,x就越小.
课堂练习
难点巩固
小结
一次函数函数的图象和性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
是一条直线,
与y轴的交点是(0,b),
与x轴的交点是( -b/k,0),
图象
性质
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.
两点法快速画出一次函数图象
谢谢!再见!
