八年级数学下册课件-19.3 课题学习 选择方案-人教版(30张)
文档属性
| 名称 | 八年级数学下册课件-19.3 课题学习 选择方案-人教版(30张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 00:00:00 | ||
图片预览







文档简介
采购员
节能灯
白炽灯
你现在是小采购员,想在两种灯中选购一种,0.01千瓦的节能灯60元,0.06千瓦的白炽灯3元,两种灯照明效果一样,使用寿命也相同(3000小时以上). 如果电费是0.5元/ (千瓦·时),当照明时间为多少小时时,两种灯费用相同?节能灯省费用?白炽灯省费用?
小显身手
费用=电费+灯的售价
电费=单价×耗电量
耗电量(度)=功率(千瓦)×用电时间(小时)
费用=单价×功率(千瓦)×用电时间(小时)+灯的售价
问题1:费用包括什么?
问题2:电费怎么算?
问题3:耗电量怎么算?
问题4:用题中已知条件表示费用?
你现在是小采购员,想在两种灯中选购一种,0.01千瓦的节能灯60元,0.06千瓦的白炽灯3元,两种灯照明效果一样,使用寿命也相同(3000小时以上). 如果电费是0.5元/ (千瓦·时),当照明时间为多少小时时,两种灯费用相同?节能灯省费用?白炽灯省费用?
锋芒初露
解:设照明时间为x小时,则节能灯的总费用y1为
y1= 0.5×0.01x+60
白炽灯的总费用y2为
y2= 0.5×0.06x+3
费用=单价×功率(千瓦)×用电时间(小时)+灯的售价
即:0.5×0.01x+60<0.5×0.06x+3 解得x>2280
?选择两种灯费用相同:
?选择白炽灯节省费用:
?选择节能灯节省费用:
即:0.5×0.01x+60=0.5×0.06x+3 解得x=2280
答:当x=2280时选用两种灯总费用一样
当x<2280时选用白炽灯节省费用
当x>2280时选用节能灯节省费用
即:0.5×0.01x+60>0.5×0.06x+3 解得x<2280
解:设照明时间为x小时,则节能灯的总费用y1为
y1= 0.5×0.01x+60
白炽灯的总费用y2为
y2= 0.5×0.06x+3
y1= y2
y1> y2
y1< y2
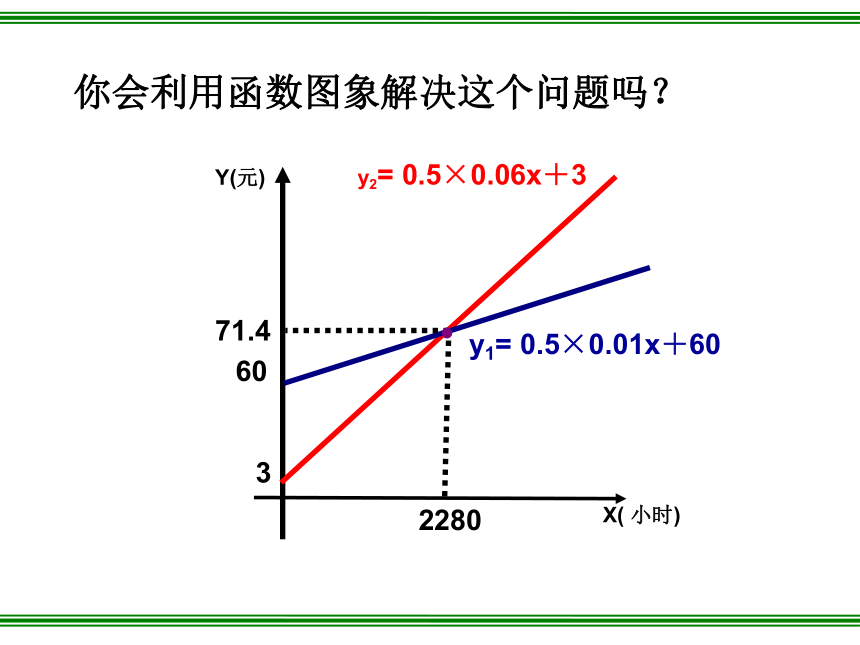
你会利用函数图象解决这个问题吗?
Y(元)
X( 小时)
2280
71.4
60
3
y1= 0.5×0.01x+60
y2= 0.5×0.06x+3
竞聘公司经理
要求:为公司设计网费
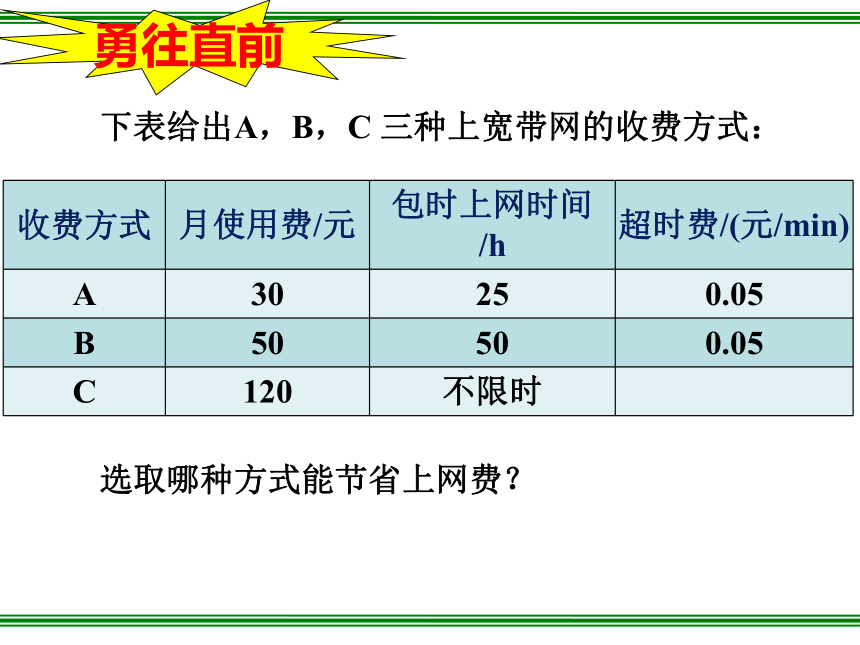
下表给出A,B,C 三种上宽带网的收费方式:
选取哪种方式能节省上网费?
勇往直前
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
分析问题:怎样选取上网收费方式
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
方式A费用:
方式B费用:
方式C费用:
yA=
30, 0≤x≤25;
3x-45, x>25.
yB=
50, 0≤x≤50;
3x-100,x>50.
yC=120,x≥0
请分别写出三种方案的上网费用y 元与上网时间x h
之间的函数解析式.
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
比较
yA 、 yB、yC
的大小
当上网时间_________
时,选择方式A最省钱.
当上网时间________
时,选择方式B最省钱.
当上网时间______
时,选择方式C最省钱.
A
B
C
经理
公司计划在总费用2 300 元的限额内,租用汽车
送234 名员工和6 名经理集体外出活动,每辆汽车上至少要有1 名经理.现在有甲、乙两种大客车,它们的载客量和租金如下表:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金(单位:元/辆)
400
280
再接再厉
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金(单位:元/辆)
400
280
(1)共需租多少辆汽车?
公司计划在总费用2 300 元的限额内,租用汽车送234 名员工和6 名经理集体外出活动,每辆汽车上至少要有1 名经理.现在有甲、乙两种大客车,它们的载客量和租金如下表:
则共需租6辆汽车。
(1)单独租甲种车;
(2)单独租乙种车;
(3)甲种车和乙种车都租.
单独租甲种车要6辆
单独租乙种车要8辆
说明租车数不小于6
说明租车数不大于8
6 ≤ 租车数辆 ≤ 8
说明租车数不大于6
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金(单位:元/辆)
400
280
(2)给出最节省费用的租车方案.
公司计划在总费用2 300 元的限额内,租用汽车送234 名员工和6 名经理集体外出活动,每辆汽车上至少要有1 名经理.现在有甲、乙两种大客车,它们的载客量和租金如下表:
设租用x辆甲种客车,则租车费用y(单位:元)是 x 的函数,即
y=400x+280(6-x)
X
6-X
化简为: y=120x+1680
设租用x辆甲种客车,则租车费用y(元)是 x 的函数,即y=120x+1680
①保证240人都有座位
即45x+30(6-x) ≥240
15x≥60
x≥4
座位数≥ 240
②保证租车费不超过2300元
租车费≤2300
即x=4或x=5
120x+1680≤2300
120x≤620
x≤
∴4≤x≤
甲种客车4辆,乙种客车2辆;
甲种客车5辆,乙种客车1辆;
此时租车费y1=120×4+1680=2160
此时租车费y2=120×5+1680=2280
应选择方案一,它比方案二节约120元.
租车费用y(元)与租甲种客车x(辆)之间的函数
关系式为 y=120x+1680
①当x=4时:
②当x=5时:
1、建立数学模型——列出函数关系式.
2、通过解不等式或利用图象来确定自变量的取值范围。
3、选择出最佳方案。
我校一老师暑期带领学校市级“三好学生”去北京旅游,甲旅行社说:“如果老师买全票一张,则其余的学生可以享受半价优惠”.乙旅行社说:“包括老师全部按全票价的6折优惠”.已知全票价为240元.
(1)当学生人数是多少时,两家旅行社的收费一样? (2)若学生人数为9人时,哪家收费低? (3)若学生人数为3人时,哪家收费低? (4)你能否猜测出当学生人数在哪个范围时选用甲旅行社?
公司需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同,设汽车每月行驶x km,应付给个体车主的月租费是y1 元,付给出租公司的月租费是y2 元,y1,y2分别与x之间的函数关系图象是如图所示的两条直线,观察图像,回答下列问题:
1000
2000
500
1500
1000
2000
2500
X(km)
y(元)
0
y
1
y
2
1000
2000
500
1500
1000
2000
2500
X(km)
y(元)
0
y
1
y
2
(1)每月行驶的路程在什么范围内时,租国有出租公司的出租车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果公司估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
当0<x<1500时,
租国有的合算。
当x=1500km时,
两家一样。
租个体车主的车合算.
为了让我校师生及市民更好的了解预防H1N1的相关知识, 我们特别制作了宣传海报,甲印刷厂提出每份材料收0.2元印刷费,另收500元的制版费,乙印刷厂提出每份材料收0.4元印刷费,不收制版费:
(1)分别写出两印刷厂的收费y(元)与印制数量x(份)之间的函数关系式;
(2)在同一坐标系中画出这两个函数的图像;
(3)我校要印制2400份宣传材料,应选择哪家印刷厂较合算?
(4)我校拿出2000元用于印制宣传材料,哪家印刷厂印制的多?多多少份?
提示:根据题意可知y是x的一次函数,得出
y甲=0.2x+500
y乙=0.4x
2400
2000
y乙=0.4x
y甲=0.2x+500
1000
2500
Y(元)
X(份)
o
500
1500
2. 小明用的练习本可以到甲商店购买,也可以到
乙商店购买,已知两商店的标价都是每本1
元,但甲商店的优惠条件是:购买10本以上,
从第11本开始以按标价的70﹪卖;乙商店的优
惠条件是:从第1本开始就按标价的85﹪卖.
(1)小明要买20本时,到哪个商店购买较省钱?
(2)分别写出甲乙两商店中,收款y(元)与购买本
数x(本)(x>10)的函数关系式.
(3)小明现有24元钱,最多可买多少本?
一样
y1=3+0.7x
y2=0.85x
30
为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗如下表:
A型
B型
价格(万元/台)
12
10
处理污水量(吨/月)
240
200
年消耗费(万元/台)
1
1
经预算,该企业购买设备的资金不高于105万元
(1)求购买设备的资金y万元与购买A型x台的函数关系,并设计该企业有几种购买方案
y=12x+10(10-x)
即 y=2x+100
∵y=2x+100≤105
∴ x≤2.5
又∵x是非负整数
∴x可取0、1、2
∴有三种购买方案:①购A型0台,B型10台;②购A型1台,B型9台;③购A型2台,B型8台.
(1)求购买设备的资金y万元与购买A型x台的函数关系,并设计该企业有几种购买方案
A型
B型
价格(万元/台)
12
10
处理污水量(吨/月)
240
200
年消耗费(万元/台)
1
1
(2)若企业每月产生的污水量为2040吨,利用函数的知识说明,应该选哪种购买方案?
A型
B型
价格(万元/台)
12
10
处理污水量(吨/月)
240
200
年消耗费(万元/台)
1
1
A型x台
则B型10-x台
解:由题意得240x+200(10-x) ≥2040
解得 x≥1
∴x为1或2
∵k>0∴y随x增大而增大.
即: 为节约资金,应选购A型1台,B型9台
节能灯
白炽灯
你现在是小采购员,想在两种灯中选购一种,0.01千瓦的节能灯60元,0.06千瓦的白炽灯3元,两种灯照明效果一样,使用寿命也相同(3000小时以上). 如果电费是0.5元/ (千瓦·时),当照明时间为多少小时时,两种灯费用相同?节能灯省费用?白炽灯省费用?
小显身手
费用=电费+灯的售价
电费=单价×耗电量
耗电量(度)=功率(千瓦)×用电时间(小时)
费用=单价×功率(千瓦)×用电时间(小时)+灯的售价
问题1:费用包括什么?
问题2:电费怎么算?
问题3:耗电量怎么算?
问题4:用题中已知条件表示费用?
你现在是小采购员,想在两种灯中选购一种,0.01千瓦的节能灯60元,0.06千瓦的白炽灯3元,两种灯照明效果一样,使用寿命也相同(3000小时以上). 如果电费是0.5元/ (千瓦·时),当照明时间为多少小时时,两种灯费用相同?节能灯省费用?白炽灯省费用?
锋芒初露
解:设照明时间为x小时,则节能灯的总费用y1为
y1= 0.5×0.01x+60
白炽灯的总费用y2为
y2= 0.5×0.06x+3
费用=单价×功率(千瓦)×用电时间(小时)+灯的售价
即:0.5×0.01x+60<0.5×0.06x+3 解得x>2280
?选择两种灯费用相同:
?选择白炽灯节省费用:
?选择节能灯节省费用:
即:0.5×0.01x+60=0.5×0.06x+3 解得x=2280
答:当x=2280时选用两种灯总费用一样
当x<2280时选用白炽灯节省费用
当x>2280时选用节能灯节省费用
即:0.5×0.01x+60>0.5×0.06x+3 解得x<2280
解:设照明时间为x小时,则节能灯的总费用y1为
y1= 0.5×0.01x+60
白炽灯的总费用y2为
y2= 0.5×0.06x+3
y1= y2
y1> y2
y1< y2
你会利用函数图象解决这个问题吗?
Y(元)
X( 小时)
2280
71.4
60
3
y1= 0.5×0.01x+60
y2= 0.5×0.06x+3
竞聘公司经理
要求:为公司设计网费
下表给出A,B,C 三种上宽带网的收费方式:
选取哪种方式能节省上网费?
勇往直前
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
分析问题:怎样选取上网收费方式
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
方式A费用:
方式B费用:
方式C费用:
yA=
30, 0≤x≤25;
3x-45, x>25.
yB=
50, 0≤x≤50;
3x-100,x>50.
yC=120,x≥0
请分别写出三种方案的上网费用y 元与上网时间x h
之间的函数解析式.
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
比较
yA 、 yB、yC
的大小
当上网时间_________
时,选择方式A最省钱.
当上网时间________
时,选择方式B最省钱.
当上网时间______
时,选择方式C最省钱.
A
B
C
经理
公司计划在总费用2 300 元的限额内,租用汽车
送234 名员工和6 名经理集体外出活动,每辆汽车上至少要有1 名经理.现在有甲、乙两种大客车,它们的载客量和租金如下表:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金(单位:元/辆)
400
280
再接再厉
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金(单位:元/辆)
400
280
(1)共需租多少辆汽车?
公司计划在总费用2 300 元的限额内,租用汽车送234 名员工和6 名经理集体外出活动,每辆汽车上至少要有1 名经理.现在有甲、乙两种大客车,它们的载客量和租金如下表:
则共需租6辆汽车。
(1)单独租甲种车;
(2)单独租乙种车;
(3)甲种车和乙种车都租.
单独租甲种车要6辆
单独租乙种车要8辆
说明租车数不小于6
说明租车数不大于8
6 ≤ 租车数辆 ≤ 8
说明租车数不大于6
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金(单位:元/辆)
400
280
(2)给出最节省费用的租车方案.
公司计划在总费用2 300 元的限额内,租用汽车送234 名员工和6 名经理集体外出活动,每辆汽车上至少要有1 名经理.现在有甲、乙两种大客车,它们的载客量和租金如下表:
设租用x辆甲种客车,则租车费用y(单位:元)是 x 的函数,即
y=400x+280(6-x)
X
6-X
化简为: y=120x+1680
设租用x辆甲种客车,则租车费用y(元)是 x 的函数,即y=120x+1680
①保证240人都有座位
即45x+30(6-x) ≥240
15x≥60
x≥4
座位数≥ 240
②保证租车费不超过2300元
租车费≤2300
即x=4或x=5
120x+1680≤2300
120x≤620
x≤
∴4≤x≤
甲种客车4辆,乙种客车2辆;
甲种客车5辆,乙种客车1辆;
此时租车费y1=120×4+1680=2160
此时租车费y2=120×5+1680=2280
应选择方案一,它比方案二节约120元.
租车费用y(元)与租甲种客车x(辆)之间的函数
关系式为 y=120x+1680
①当x=4时:
②当x=5时:
1、建立数学模型——列出函数关系式.
2、通过解不等式或利用图象来确定自变量的取值范围。
3、选择出最佳方案。
我校一老师暑期带领学校市级“三好学生”去北京旅游,甲旅行社说:“如果老师买全票一张,则其余的学生可以享受半价优惠”.乙旅行社说:“包括老师全部按全票价的6折优惠”.已知全票价为240元.
(1)当学生人数是多少时,两家旅行社的收费一样? (2)若学生人数为9人时,哪家收费低? (3)若学生人数为3人时,哪家收费低? (4)你能否猜测出当学生人数在哪个范围时选用甲旅行社?
公司需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同,设汽车每月行驶x km,应付给个体车主的月租费是y1 元,付给出租公司的月租费是y2 元,y1,y2分别与x之间的函数关系图象是如图所示的两条直线,观察图像,回答下列问题:
1000
2000
500
1500
1000
2000
2500
X(km)
y(元)
0
y
1
y
2
1000
2000
500
1500
1000
2000
2500
X(km)
y(元)
0
y
1
y
2
(1)每月行驶的路程在什么范围内时,租国有出租公司的出租车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果公司估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
当0<x<1500时,
租国有的合算。
当x=1500km时,
两家一样。
租个体车主的车合算.
为了让我校师生及市民更好的了解预防H1N1的相关知识, 我们特别制作了宣传海报,甲印刷厂提出每份材料收0.2元印刷费,另收500元的制版费,乙印刷厂提出每份材料收0.4元印刷费,不收制版费:
(1)分别写出两印刷厂的收费y(元)与印制数量x(份)之间的函数关系式;
(2)在同一坐标系中画出这两个函数的图像;
(3)我校要印制2400份宣传材料,应选择哪家印刷厂较合算?
(4)我校拿出2000元用于印制宣传材料,哪家印刷厂印制的多?多多少份?
提示:根据题意可知y是x的一次函数,得出
y甲=0.2x+500
y乙=0.4x
2400
2000
y乙=0.4x
y甲=0.2x+500
1000
2500
Y(元)
X(份)
o
500
1500
2. 小明用的练习本可以到甲商店购买,也可以到
乙商店购买,已知两商店的标价都是每本1
元,但甲商店的优惠条件是:购买10本以上,
从第11本开始以按标价的70﹪卖;乙商店的优
惠条件是:从第1本开始就按标价的85﹪卖.
(1)小明要买20本时,到哪个商店购买较省钱?
(2)分别写出甲乙两商店中,收款y(元)与购买本
数x(本)(x>10)的函数关系式.
(3)小明现有24元钱,最多可买多少本?
一样
y1=3+0.7x
y2=0.85x
30
为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗如下表:
A型
B型
价格(万元/台)
12
10
处理污水量(吨/月)
240
200
年消耗费(万元/台)
1
1
经预算,该企业购买设备的资金不高于105万元
(1)求购买设备的资金y万元与购买A型x台的函数关系,并设计该企业有几种购买方案
y=12x+10(10-x)
即 y=2x+100
∵y=2x+100≤105
∴ x≤2.5
又∵x是非负整数
∴x可取0、1、2
∴有三种购买方案:①购A型0台,B型10台;②购A型1台,B型9台;③购A型2台,B型8台.
(1)求购买设备的资金y万元与购买A型x台的函数关系,并设计该企业有几种购买方案
A型
B型
价格(万元/台)
12
10
处理污水量(吨/月)
240
200
年消耗费(万元/台)
1
1
(2)若企业每月产生的污水量为2040吨,利用函数的知识说明,应该选哪种购买方案?
A型
B型
价格(万元/台)
12
10
处理污水量(吨/月)
240
200
年消耗费(万元/台)
1
1
A型x台
则B型10-x台
解:由题意得240x+200(10-x) ≥2040
解得 x≥1
∴x为1或2
∵k>0∴y随x增大而增大.
即: 为节约资金,应选购A型1台,B型9台
