八年级数学下册课件-20.1.2 中位数和众数-人教版(21张)
文档属性
| 名称 | 八年级数学下册课件-20.1.2 中位数和众数-人教版(21张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 736.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 19:49:11 | ||
图片预览






文档简介
中位数与 众数
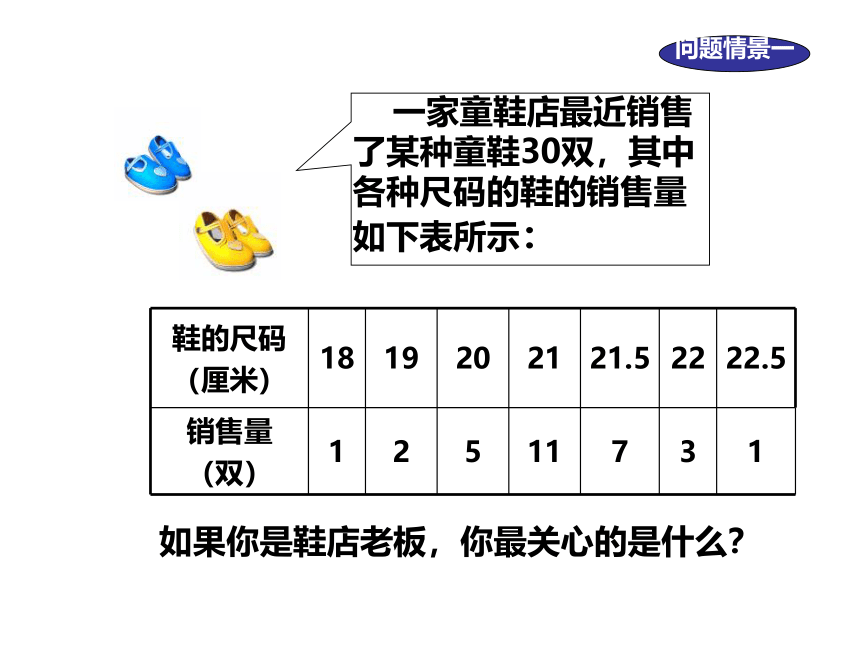
鞋的尺码
(厘米)
18
19
20
21
21.5
22
22.5
销售量
(双)
1
2
5
11
7
3
1
问题情景一
一家童鞋店最近销售了某种童鞋30双,其中各种尺码的鞋的销售量如下表所示:
如果你是鞋店老板,你最关心的是什么?
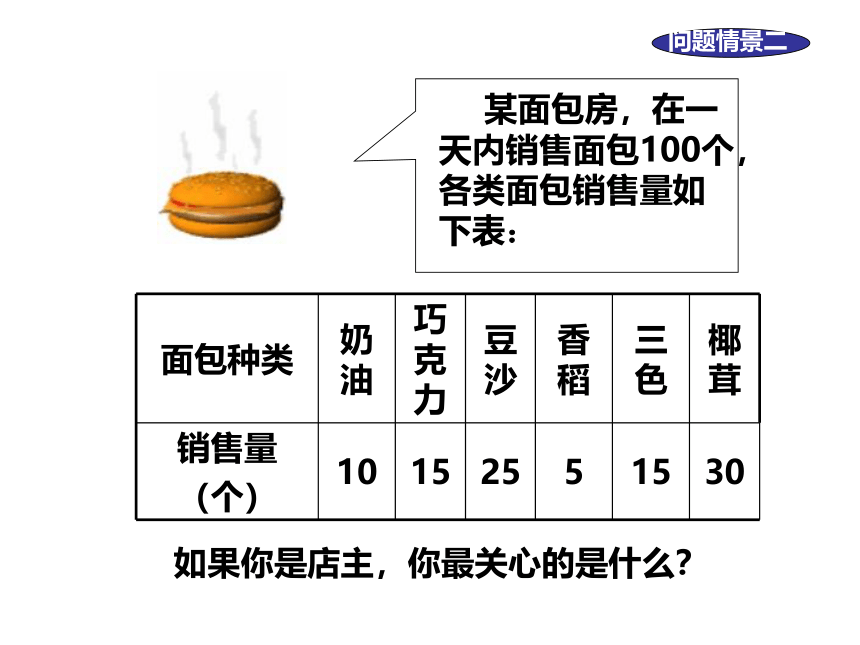
某面包房,在一天内销售面包100个,各类面包销售量如下表:
面包种类
奶油
巧克力
豆沙
香稻
三色
椰茸
销售量
(个)
10
15
25
5
15
30
问题情景二
如果你是店主,你最关心的是什么?
招工启事
因我公司扩大规模,现需招若干名员工。我公司员工收入很高,月平均工资2000元。有意者于2004年12月20日到我处面试。
辉煌公司人事部
2004年12月18日
我公司员工收入很高,月平均工资2000元
经理
应聘者
这个公司员工收入到底怎样?
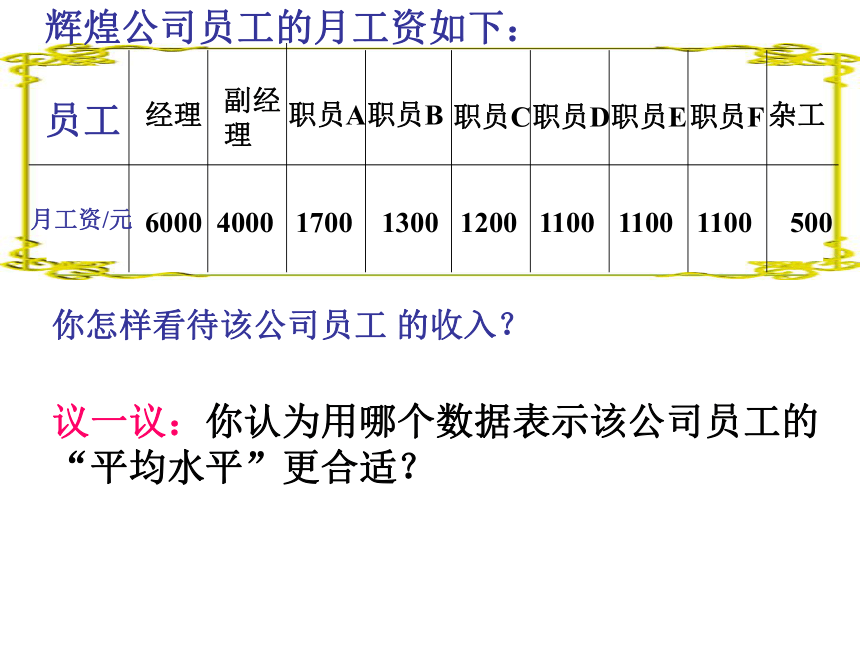
辉煌公司员工的月工资如下:
员工
月工资/元
经理
副经 理
职员A
职员B
职员F
职员E
职员D
职员C
杂工
6000
4000
1700
1300
1200
1100
1100
1100
500
你怎样看待该公司员工 的收入?
议一议:你认为用哪个数据表示该公司员工的“平均水平”更合适?
定义:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数。
注意:1.求中位数要将一组数据按大小顺序,而不必计算,顾名思义,中位数就是位置处于最中间的一个数(或最中间的两个数的平均数),排序时,从小到大或从大到小都可以.
2.当数据个数为奇数时,中位数是这组数据中的一个数据;但当数据个数为偶数时,其中位数是最中间两个数据的平均数,它不一定与这组数据中的某个数据相等。
定义:
在一组数据中,出现次数最多的数据叫做这组数据的众数.
注意:
(1) 众数是一组数据中出现次数最多的数据,是一组数据中的原数据,而不是相应的次数.
(2) 一组数据中的众数有时不只一个,如数据2、3、-1、2、1、3中,2和3都出现了2次,它们都是这组数据的众数.
1、在一次数学竞赛中,5名学生的成绩从低分到高分排列名次是:
55 57 61 62 98
那么,它们的中位数是多少?
练一练
2、10名工人某天生产同一零件,生产的件数是:
15 17 14 10 15
19 17 16 14 12
求这一天10名工人生产的零件的中位数。
练一练
3、 在一次英语口试中,20名学生的得分如下 :
80 100 60 80 70 90 50 80 70
80 70 90 80 90 80 70 90 60 80
求这次英语口试中学生得分的众数。
分析:如何求出众数呢?关键是统计相同数据的个
数。可仿照情景一表格写正号统计,找出众数;也
可用观察法找出这组数据中哪些数据出现的次数较
多,从而进一步找出它的众数。
1、在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示:
成绩米
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的众数,中位数与平均数(计算结果保留到小数点后第2位)。
试一试
答案: 众数是1.75米,中位数是1.70米, 平均数是1.69米。
2、已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,求x值及这组数据的中位数。
解:∵10,10,x,8的中位数与平均数相等
∴ (10+x)/2= (10+10+x+8)/4
∴x=8, (10+x)/2=9
∴这组数据中的中位数是9。
试一试
试一试
3、某校初二年级有4个班级参加了植树活动,已知在同一天这4个班级植树的棵数分别为50,50,40,x,如果这组数据的众数和平均数正好相等,那么这组数据的中位数 是多少?
想一想
某地举办体操比赛,由7位评委现场给运动员打分,已知7位评委给某运动员的评分如下:
请你利用所学的统计知识,从不同角度给出这位运动员的最后得分。(精确到0.01)
这节课有何收获?
1. 知识小结:这节课我们学习了众数、中位数的概念,了解了它们在描述一组数据“平均水平” 时的不同角度和适用范围。
2.方法小结:①众数由所给数据可直接求出,(一组数据中的众数可能不止一个,众数是一组数据中出现的次数最多的数据,而不是该数据出现的次数.如果有两个数据出现的次数相同,并且比其他数据出现次数都多,那么这两个数据都是这组数据的众数)。
②求中位数时,首先要先排序(从小到大或从大到小),然后计算中位数的序号,分数据为奇数个与偶数个两种来求.(既找出最中间的一个数据或最中间两个数并算出它们的平均数)。
3.知识网络:平均数、众数及中位数都是描述一组数据的集中趋势的特征数,但描述的角度和适用范围有所不同。平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动;众数着眼于对各数据出现的频数的考察,其大小只与这组数据中的部分数据有关。当一组数据中有不少数据多次重复出现时,其众数往往是我们关心的一种统计量;中位数则仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时,可用它来描述其集中趋势。
调查本班中学生所穿鞋的尺码,得到平均数、中位数与众数。
作业本(2)P41
伴你学数学P96练习三
鞋的尺码
(厘米)
18
19
20
21
21.5
22
22.5
销售量
(双)
1
2
5
11
7
3
1
问题情景一
一家童鞋店最近销售了某种童鞋30双,其中各种尺码的鞋的销售量如下表所示:
如果你是鞋店老板,你最关心的是什么?
某面包房,在一天内销售面包100个,各类面包销售量如下表:
面包种类
奶油
巧克力
豆沙
香稻
三色
椰茸
销售量
(个)
10
15
25
5
15
30
问题情景二
如果你是店主,你最关心的是什么?
招工启事
因我公司扩大规模,现需招若干名员工。我公司员工收入很高,月平均工资2000元。有意者于2004年12月20日到我处面试。
辉煌公司人事部
2004年12月18日
我公司员工收入很高,月平均工资2000元
经理
应聘者
这个公司员工收入到底怎样?
辉煌公司员工的月工资如下:
员工
月工资/元
经理
副经 理
职员A
职员B
职员F
职员E
职员D
职员C
杂工
6000
4000
1700
1300
1200
1100
1100
1100
500
你怎样看待该公司员工 的收入?
议一议:你认为用哪个数据表示该公司员工的“平均水平”更合适?
定义:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数。
注意:1.求中位数要将一组数据按大小顺序,而不必计算,顾名思义,中位数就是位置处于最中间的一个数(或最中间的两个数的平均数),排序时,从小到大或从大到小都可以.
2.当数据个数为奇数时,中位数是这组数据中的一个数据;但当数据个数为偶数时,其中位数是最中间两个数据的平均数,它不一定与这组数据中的某个数据相等。
定义:
在一组数据中,出现次数最多的数据叫做这组数据的众数.
注意:
(1) 众数是一组数据中出现次数最多的数据,是一组数据中的原数据,而不是相应的次数.
(2) 一组数据中的众数有时不只一个,如数据2、3、-1、2、1、3中,2和3都出现了2次,它们都是这组数据的众数.
1、在一次数学竞赛中,5名学生的成绩从低分到高分排列名次是:
55 57 61 62 98
那么,它们的中位数是多少?
练一练
2、10名工人某天生产同一零件,生产的件数是:
15 17 14 10 15
19 17 16 14 12
求这一天10名工人生产的零件的中位数。
练一练
3、 在一次英语口试中,20名学生的得分如下 :
80 100 60 80 70 90 50 80 70
80 70 90 80 90 80 70 90 60 80
求这次英语口试中学生得分的众数。
分析:如何求出众数呢?关键是统计相同数据的个
数。可仿照情景一表格写正号统计,找出众数;也
可用观察法找出这组数据中哪些数据出现的次数较
多,从而进一步找出它的众数。
1、在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示:
成绩米
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的众数,中位数与平均数(计算结果保留到小数点后第2位)。
试一试
答案: 众数是1.75米,中位数是1.70米, 平均数是1.69米。
2、已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,求x值及这组数据的中位数。
解:∵10,10,x,8的中位数与平均数相等
∴ (10+x)/2= (10+10+x+8)/4
∴x=8, (10+x)/2=9
∴这组数据中的中位数是9。
试一试
试一试
3、某校初二年级有4个班级参加了植树活动,已知在同一天这4个班级植树的棵数分别为50,50,40,x,如果这组数据的众数和平均数正好相等,那么这组数据的中位数 是多少?
想一想
某地举办体操比赛,由7位评委现场给运动员打分,已知7位评委给某运动员的评分如下:
请你利用所学的统计知识,从不同角度给出这位运动员的最后得分。(精确到0.01)
这节课有何收获?
1. 知识小结:这节课我们学习了众数、中位数的概念,了解了它们在描述一组数据“平均水平” 时的不同角度和适用范围。
2.方法小结:①众数由所给数据可直接求出,(一组数据中的众数可能不止一个,众数是一组数据中出现的次数最多的数据,而不是该数据出现的次数.如果有两个数据出现的次数相同,并且比其他数据出现次数都多,那么这两个数据都是这组数据的众数)。
②求中位数时,首先要先排序(从小到大或从大到小),然后计算中位数的序号,分数据为奇数个与偶数个两种来求.(既找出最中间的一个数据或最中间两个数并算出它们的平均数)。
3.知识网络:平均数、众数及中位数都是描述一组数据的集中趋势的特征数,但描述的角度和适用范围有所不同。平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动;众数着眼于对各数据出现的频数的考察,其大小只与这组数据中的部分数据有关。当一组数据中有不少数据多次重复出现时,其众数往往是我们关心的一种统计量;中位数则仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时,可用它来描述其集中趋势。
调查本班中学生所穿鞋的尺码,得到平均数、中位数与众数。
作业本(2)P41
伴你学数学P96练习三
