湘教版(2012)初中数学九年级上册 3.2 平行线分线段成比例 导学案
文档属性
| 名称 | 湘教版(2012)初中数学九年级上册 3.2 平行线分线段成比例 导学案 | 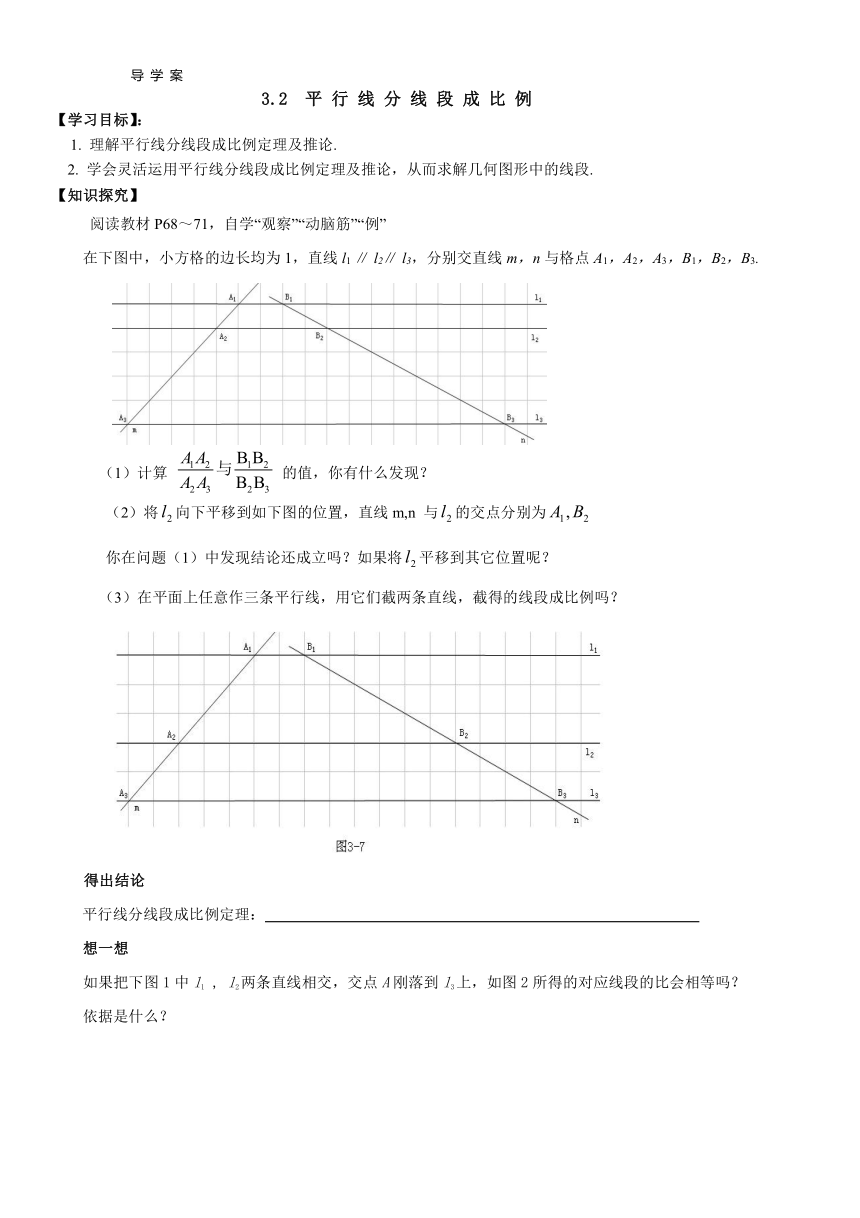 | |
| 格式 | zip | ||
| 文件大小 | 112.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 19:58:14 | ||
图片预览

文档简介
导
学
案
3.2
平
行
线
分
线
段
成
比
例
【学习目标】:
1.
理解平行线分线段成比例定理及推论.
2.
学会灵活运用平行线分线段成比例定理及推论,从而求解几何图形中的线段.
【知识探究】
阅读教材P68~71,自学“观察”“动脑筋”“例”
在下图中,小方格的边长均为1,直线l1
∥
l2∥
l3,分别交直线m,n与格点A1,A2,A3,B1,B2,B3.
(1)计算
的值,你有什么发现?
(2)将向下平移到如下图的位置,直线m,n
与的交点分别为
你在问题(1)中发现结论还成立吗?如果将平移到其它位置呢?
(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?
得出结论
平行线分线段成比例定理:
想一想
如果把下图1中l1
,
l2两条直线相交,交点A刚落到l3上,如图2所得的对应线段的比会相等吗?
依据是什么?
得出结论:(推论)
平行于三角形一边的直线截其他两边,所得的对应线段
.
【学习反馈】
如图,l1,l2分别被l3,l4,l5所截,且l3∥l4∥l5,则AB与________对应,BC与________对应,
DF与________对应;=,=,==.
2.如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
A.
=
B.
=
C.
=
D.
=
【当堂检测】:
1.
如图,,,,
,则等于__________.
2.
如图,在△ABC中,DE∥BC,AD=3,DB=4,CE=4,
则AE=(
)
A.2
B.3
C.4
D.5
3.如图,在中,点D,E分别在AB,AC边上,DE∥BC,已知,则等于______.
4.如图,AB∥MN,BC∥NG,求证:.
【学后反思】
学
案
3.2
平
行
线
分
线
段
成
比
例
【学习目标】:
1.
理解平行线分线段成比例定理及推论.
2.
学会灵活运用平行线分线段成比例定理及推论,从而求解几何图形中的线段.
【知识探究】
阅读教材P68~71,自学“观察”“动脑筋”“例”
在下图中,小方格的边长均为1,直线l1
∥
l2∥
l3,分别交直线m,n与格点A1,A2,A3,B1,B2,B3.
(1)计算
的值,你有什么发现?
(2)将向下平移到如下图的位置,直线m,n
与的交点分别为
你在问题(1)中发现结论还成立吗?如果将平移到其它位置呢?
(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?
得出结论
平行线分线段成比例定理:
想一想
如果把下图1中l1
,
l2两条直线相交,交点A刚落到l3上,如图2所得的对应线段的比会相等吗?
依据是什么?
得出结论:(推论)
平行于三角形一边的直线截其他两边,所得的对应线段
.
【学习反馈】
如图,l1,l2分别被l3,l4,l5所截,且l3∥l4∥l5,则AB与________对应,BC与________对应,
DF与________对应;=,=,==.
2.如图所示,已知AB∥CD∥EF,那么下列结论正确的是( )
A.
=
B.
=
C.
=
D.
=
【当堂检测】:
1.
如图,,,,
,则等于__________.
2.
如图,在△ABC中,DE∥BC,AD=3,DB=4,CE=4,
则AE=(
)
A.2
B.3
C.4
D.5
3.如图,在中,点D,E分别在AB,AC边上,DE∥BC,已知,则等于______.
4.如图,AB∥MN,BC∥NG,求证:.
【学后反思】
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
