5.6 函数 y=Asin( ωx + φ)(Word解析版)
文档属性
| 名称 | 5.6 函数 y=Asin( ωx + φ)(Word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 12.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 20:31:11 | ||
图片预览



文档简介
高中数学同步练习 人教A版 第一册
5.6 函数 y=Asin( ωx + φ)
一、单选题(共10题;共20分)
1.把函数 图象上各点的横坐标缩短到原来的 倍(纵坐标不变),再将图象向右平移 个单位,得到函数 ,那么 的值为(?? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
2.要得到函数 的图像,只需要将函数 的图像(??? )
A.?向左平移 个单位?????B.?向右平移 个单位?????C.?向左平移 个单位?????D.?向右平移 个单位
3.已知函数 ( , , )的部分图象如图所示,若将函数 的图象向右平移 个单位后,得到一个偶函数的图象,则 的取值可能为(??? )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
4.函数 _????°???????è±????_每个点的纵坐标保持不变,横坐标扩大为原来的2倍,然后再将它的图形沿x轴向左平移 个单位,得到函数 的图象,则函数 的解析式是(?? ?)
A.????????????B.????????????C.????????????D.?
5.为了得到函数 的图像,只需将函数 的图像(??? )
A.?向右平移 个单位??????B.?向右平移 个单位??????C.?向左平移 个单位??????D.?向左平移 个单位2-1-c-n-j-y
6.函数 的图像可以由 的图像(??? )个单位得到.
A.?向左平移 ?????????????????????B.?向右平移 ?????????????????????C.?向左平移 ?????????????????????D.?向右平移
7.为了得到函数 的图象,可以将函数 的图象( ??)
A.?向右平移
B.?向左平移 个单位
C.?向右平移 个单位
D.?向左平移 个单位
8.为了得到函数 的图象,只需把函数 的图象(??? )
A.?向左平移 _?????????é???????_????????????????????????????????????B.?向左平移 个单位长度
C.?向右平移 个单位长度?????????????????????????????????????D.?向右平移 个单位长度
9.若 的最小值为-2,其图像相邻最高点与最低点横坐标之差为 ,且图像过点(0,1),则其解析式是( ??)
A.?????????????B.?????????????C.?????????????D.?
10.已知函数 的部分图象如下图所示,则函数 的解析式(????? )
A.??????????????????????????????????????????B.?
C.???????????????????????????????????????????D.?
二、填空题(共10题;共12分)
11.把函数 的图象向左平移 个单位,得到的函数是________.
12.若两个函数的图象经过若干次平移后能够重合,则称这两个函数为“同形”函数.给出下列三个函数: 21教育名师原创作品
① ;② ;③ .
其中,为“同形”函数的序号是________.
13.已知函数 ( , , )在半个周期内的图象如图所示,则 ________.
14.把函数 图象向右平移 个单位,得函数 ( )的图象,则 的值等于________.
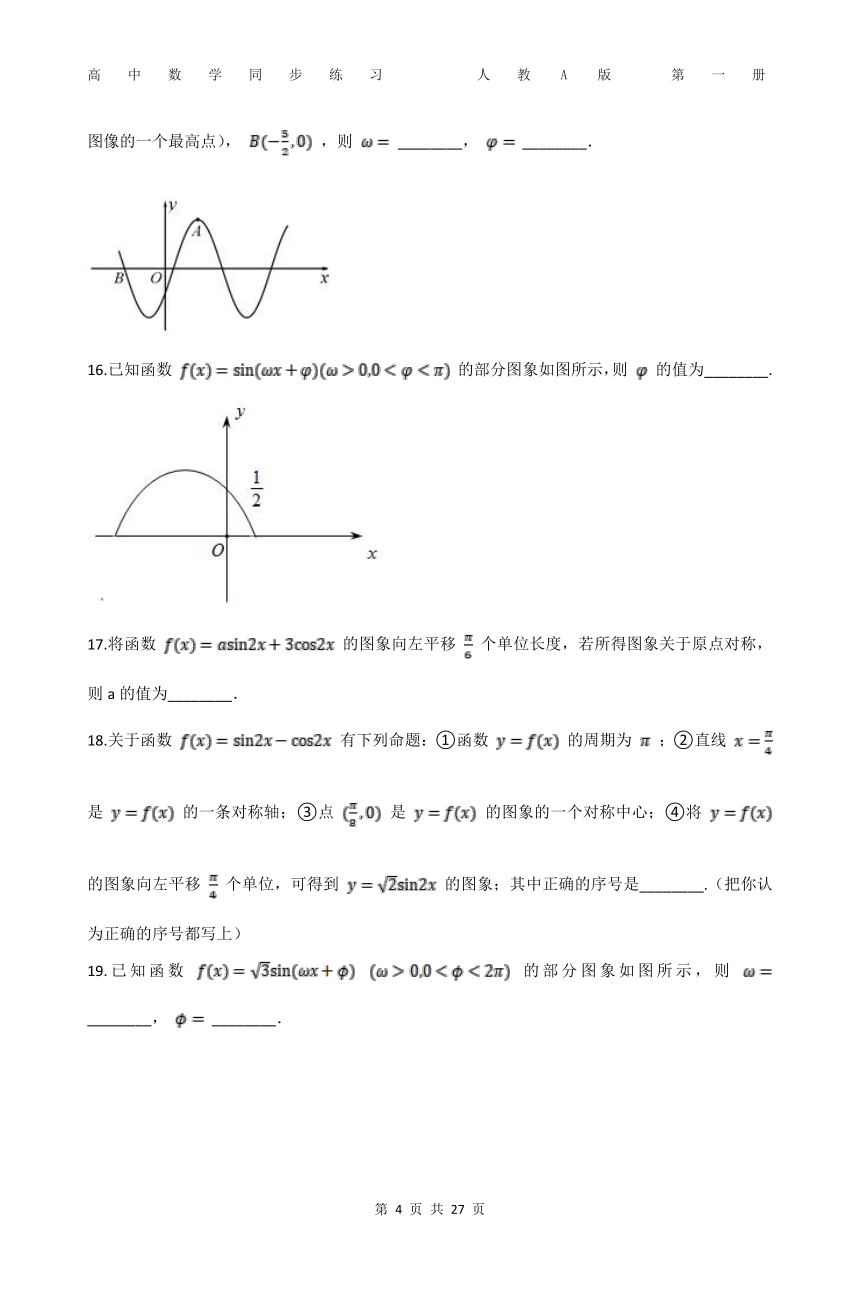
15.函数 的部分图像如图所示.若 (点A为图像的一个最高点), ,则 ________, ________.
16.已知函数 的部分图象如图所示,则 的值为________.
?
17.将函数 的图象向左平移 个单位长度,若所得图象关于原点对称,则a的值为________. 【来源:21cnj*y.co*m】
18.关于函数 有下列命题:①函数 的周期为 ;②直线 是 的一条对称轴;③点 是 的图象的一个对称中心;④将 的图象向左平移 个单位,可得到 的图象;其中正确的序号是________.(把你认为正确的序号都写上)
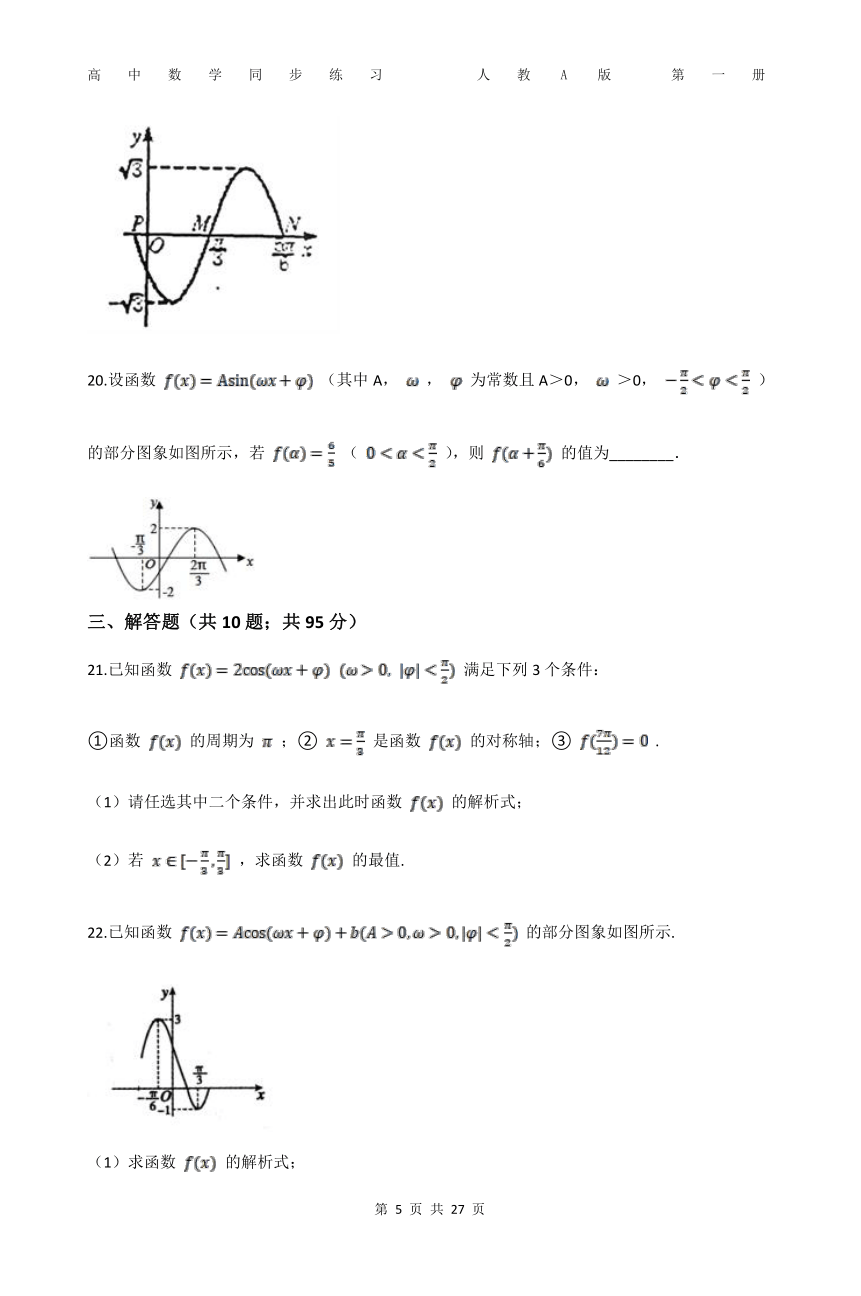
19.已知函数 的部分图象如图所示,则 ________, ________.
20.设函数 (其中A, , 为常数且A>0, >0, )的部分图象如图所示,若 ( ),则 的值为________.
三、解答题(共10题;共95分)
21.已知函数 满足下列3个条件:
①函数 的周期为 ;② 是函数 的对称轴;③ .
(1)请任选其中二个条件,并求出此时函数 的解析式;
(2)若 ,求函数 的最值.
22.已知函数 的部分图象如图所示.
(1)求函数 的解析式;
(2)求函数 在区间 上的值域.
23.设 .
(1)求使不等式 成立的x的取值集合;
(2)先将 图象_????????????????¨?_坐标伸长为原来的2倍,纵坐标不变;再向右平移 个单位;最后向下平移 个单位得到函数 的图象.若不等式 在 上恒成立,求实数 的取值范围.
24.已知函数 的部分图象如图所示.
(1)求 的解析式;
(2)求 在 上的最大值和最小值.
25.已知函数 , .
(1)将函数 _?????????è?¨?¤????_ (其中 , , , )形式;
(2)用五点法列表并作出函数 一个周期内的图象.
?????? ? ? ? ? ?
????????? ? ? ? ? ?
???????? ? ? ? ? ?
26.已知函数 .
(1)求函数 的最小正周期;
(2)若将函数 每点的横坐标变为原来的2倍,纵坐标不变,得到函数 的图象,求 在区间 上的值域. 2·1·c·n·j·y
27.已知函数 的部分图像如图所示.
(1)求 的解析式及对称中心坐标;
(2)先将 __???????????????_标缩短到原来的 倍,再向右平移 个单位,最后将图像向上平移1个单位后得到 的图像,求函数 在 上的单调增区间和最值.
28.已知函数 .
(Ⅰ)求 的最小正周期和单调递增区间;
(Ⅱ)将函数 像上所有点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图像向左平移 个单位长度,得到函数 的图像,若关于 的方程 在 上恰有2个根,求 的取值范围.
29.已知函数 .
(1)求函数 的最小正周期;
(2)将函数 的图象右移 个单位得到 的图象,求函数 的单调递增区间.
30.已知函数 , 的部分图象如图所示.
(1)求 的解析式,并说明 的图象怎样经过2次变换得到 的图象;
(2)若对于任意的 ,不等式 恒成立,求实数 的取值范围.
答案解析部分
一、单选题
1.【答案】 B
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】把函 图象上各点的横坐标缩短到原来的 倍,得到的函数图象对应的解析式为 , 21·世纪*教育网
再将图象向右平移 ,得到 ,所以 .
故答案为:B.
【分析】先根据图象变换求出 ,然后代入可得 的值.
2.【答案】 B
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】解:函数 等价于 ,
故只需要将 向右平移 即可得到.
故答案为:B.
【分析】先将函数 转化为 ,然后根据平移的规则即可得出答案.
3.【答案】 D
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由函数图像可知,
而 ,所以
由周期公式可得
所以
将最低点坐标 代入解析式可知
则
所以
因为
所以当 时,
则解析式为
将解析式向右平移 单位后,可得
因为平移后的函数为偶函数,则
解得
对比四个选项,当 时,
故答案为:D
【分析】根据部分函数图像,先求得函数解析式.结合函数平移变化,求得平移后的解析式,由平移后为偶函数并对比选项即可求解.【来源:21·世纪·教育·网】
4.【答案】 C
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】解:由题意曲 的图象沿x轴向右平移 个单位,再纵坐标不变,横坐标缩小为原来的一半即可得到 的图形,故 21*cnjy*com
的图形沿x轴向右平移 个单位所得图形对应的函数解析式为 ,然后再将所得的曲线上的点的纵坐标保持不变,横坐标缩小到原来的一半,所得的图形对应的解析式为
故答案为:C.
【分析】此类题_????????????è?????_通过反变求出原来函数的解析式,由题意可由曲线与 的图形沿x轴向右平移 个单位,再纵坐标不变,横坐标缩小为原来的一半即可得到 的解析式,选出正确选项
5.【答案】 A
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】根据函数平移变换,由 变换为 ,
只需将 的图象向右平移 个单位,即可得到 的图像,
故答案为:A.
【分析】根据函数平移变换的方法,由 即 ,只需向右平移 个单位即可.
6.【答案】 D
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】因为 ,
所以只需由 的图像向右平移 个单位得到.
故答案为:D
【分析】由 ,可以确定函数图象之间的变换,即可求解.
7.【答案】 D
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答_??????é??è????????_数图像平移变换:函数 的图像平移 单位( ,向左; ,向右)所得图像对应函数为 , 【出处:21教育名师】
将函数 的图象平移 个单位后,所得图像对应函数为
;令 ,得 ,
故答案为:D。
【分析】利用已知条件_?????????è§???????_数的图象变换,从而将函数 的图象向左平移 个单位得到函数 的图象。【版权所有:21教育】
8.【答案】 B
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答 向左平移 单位可得 ,
故答案为:B.
【分析】对比两个函数中自变量x的变化情况,再结合“左加右减”的平移原则,即可得答案;
9.【答案】 C
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由已知_???????????????A_=2,T=2× = ,故 ,又因为图像过点(0,1),所以2 =1,可得 ,所以 ,
故答案为:C.
【分析】利用三角型函数的最_?°???????-2???_从而求出A的值,再利用三角型函数图象相邻最高点与最低点横坐标之差为 ,从而结合最小正周期公式求出的值,再利用三角型函数图象过点(0,1)结合正弦函数图象点对应法,从而求出的值,从而求出三角型函数的解析式。
10.【答案】 D
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由函_??°??????è±????__
即 则 ,
则 ,
则 则
则
∵ ,∴当k=0时,
则函数 .
故答案为:D.
【分析】根据函数的图象求出A,ω 和φ的值即可.
二、填空题
11.【答案】
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】把函数 的图象向左平移 个单位,
得到的函数是 ,
故答案为 .
【分析】直接利用三角函数图象的平移变换法则求解即可.
12.【答案】 ①③
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】根据“同形”函数的定义可知,若两个函数互为“同形”函数,则两个函数的振幅相等,最小正周期也相等, www-2-1-cnjy-com
对于①中的函数 ,该函数的振幅为 ,最小正周期为 ;
对于②中的函数 ,该函数的振幅为 ,最小正周期为 ;
对于③中的函数 ,该函数的振幅为 ,最小正周期为 .
将函数 的图象向右平移 个单位长度可得到函数 的图象.
因此,为“同形”函数的序号是①③.
故答案为:①③.
【分析】将①③中的函数解析式化简,根据“同形”函数的定义可知,两个函数的振幅相等,最小正周期也相等,由此可得出结论.
13.【答案】
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】根据 的图象可知 ,
,
所以 .
由 得 ,由于 ,即 ,
,所以 .
故答案为:
【分析】根据 的图象,依次求得 和 的值.
14.【答案】
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】把函数 的图象向右平移 个单位,
所得图象对应的解析式为 ,
由题设可知 对任意的 恒成立,
故 对任意的 恒成立,
所以 ,故 即 ,
因为 ,故 ,
故答案为: .
【分析】先求出 的图象平移后所得图象对应的解析式,再利用该解析式与 完全一致可求 的值.www.21-cn-jy.com
15.【答案】 ;
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】解:因为点 为图像的一个最高点,所以 ,
由图可知, ,得 ,
所以 ,解得 ,
所以 ,
将点 坐标代入 中,得 ,
所以 , ,
因为 ,所以 ,
故答案为: ;
【分析】由点 图像的一个最高点,可求出振幅 ,再由 , 可求出周期,从而可求出 的值,然后代入其中的一个点的坐标可求出 的值.
16.【答案】
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由图可得: , 或
由于0在函数 的单调减区间内,
所以 .
故答案为:
【分析】根据图像可得 ,根据0所在位置,处于函数的单调减区间,即可得解.
17.【答案】
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】将函数 的图象向左平移 个单位长度,得解析式为 ,它的图象关于原点对称,则 ,即 , , 21教育网
故答案为: .
【分析】求出平移后的函数解析式,由新函数图象过原点得出 ,
18.【答案】 ①③
【考点】三角函数的周期性及其求法,正弦函数的奇偶性与对称性,函数y=Asin(ωx+φ)的图象变换 21*cnjy*com
【解析】【解答】 ,则函数周期为 ;当 时 ,故 不是函数的对称轴;当 时, ,故点 是 的图象的一个对称中心;将 的图象向左平移 个单位,
得到 。
故答案为:①③
【分析】化简得到 ,计算函数的周期,对称轴,对称中心,平移依次判断每个选项得到答案.
19.【答案】 2;
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由图像知道函数_????????¨??????__ ,故周期为 将函数零点代入得到 由题意可知 ,故得到 。
故答案为: ;? 。
【分析】利用三角型函数的_é?¨????????°???è±?_结合最小正周期公式和特殊点代入法,再利用正弦函数的五点对应法,从而求出函数 的解析式,从而求出的值。
20.【答案】
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由函数 的图知, ,由 ,得 ,
∴ ,
又 ,且 ,∴ ,∴ ,
由 ,∴ ,
又 ,∴ ,
∴ ,
∴
? ?
故答案为 .
【分析】由函数 _??????è±??±????A_、T、 和 的值,写出 的解析式,再由 的值,利用三角恒等变换求出 的值.21cnjy.com
三、解答题
21.【答案】 (1)解:选①②,则 ,解得 ,
因为 ,所以 ,即 ;
选①③, ,由 得 ,
因为 ,所以 ,即 ;
选②③, ,由 得 ,
因为 ,所以 ,即
(2)解:由题意得,因为 ,所以 .
所以当 即 时, 有最大值 ,
所以当 即 时, 有最小值 .
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【分析】(1) ,由②知 ,由③知 ,结合 即可求出 的解析式.(2)由 可得 ,进而可求出函数最值.
22.【答案】 (1)解:由图可知 ,解得
解得
又函数过点
即 , 解得
, ,
(2)解:
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【分_?????????1?????±_图可知 即可求出 ,再根据函数的最小正周期求出 ,又函数过点 ,代入即可求出 从而得到函数解析式;(2)由x的取值范围求出 的范围,再由余弦函数的性质解答.21世纪教育网版权所有
23.【答案】 (1) .
即:
,
所以原不等式的解集为:
(2)解: 将图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,得 ;再向右平移 个单位,得 ;最后向下平移 个单位得到函数 ,
∴ .
设 ,由 可得: ,
则原不等式等价于: 在 上恒成立;
设 , ,则 在 递增,在 递减,所以 ,
所以
【考点】函数恒成立问题,正弦函数的图象,函数y=Asin(ωx+φ)的图象变换
【解析】【分析】(1)利用_é??????????????è??_助角公式可得 ,因此 等价于 ,利用正弦函数的性质可求不等式的解集.(2)根据图象变换可得 ,从而原不等式可化为 在 ,换元后利用二次函数的性质可求 的取值范围.
24.【答案】 (1)解:由图可知 ,
,则 ,
将 代入 得 ,则 .?
因为 ,所以 .
故
(2)解:由 ,得 .
当 即 时, 取得最大值,且 ;
当 ,即 时, 取得最小值,且
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的最值
【解析】【分析】(_1?????±????¤§???_确定A,由周期确定 ,由点的坐标确定 ;(2)求出 的范围,再根据正弦函数的性质得最值.
25.【答案】 (1)解:
(2)解:列表如下:
x
y 0
0 - 0
图象如图所示:
【考点】三角函数中的恒等变换应用,五点法作函数y=Asin(ωx+φ)的图象
【解析】【分析】(1)利用_é??????????????è??_助角公式可求得 .(2)先完善表格,再依据各点绘制一个周期内的图象.
26.【答案】 (1)解:由题可知:
所以
则
所以
所以最小正周期
(2)解:由(1)可知: ,
依题变换之后
由 ,所以
所以
所以 在区间 上的值域为
【考点】三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的定义域和值域,函数y=Asin(ωx+φ)的图象变换 21·cn·jy·com
【解析】【分析】(1)根据两_è§????????·???????_弦、余弦公式并结合辅助角公式化简可得 ,然后根据周期公式简单计算可得结果.(2)根据(1)的条件,以及伸缩变换可得 ,然后使用整体法以及正弦型函数的性质可得结果.
27.【答案】 (1)解:由图知: ,解得 , ,
, 所以 ,
把点 代入得: ,
即 , ,又因为 ,所以 ,
即 ;
令 , ,解得 ,
故所求对称中心坐标为: , .
(2)解: 的图像纵坐标缩短到原来的 倍,得到 ,
再向右平移 个_??????????????°__ ,
再将图像向上平移1个单位,得到
由 , ,
解得 ,
因为 ,所以增区间为 .
因为 ,当 时, 有最大值 ,
当 时, 有最小值 .
【考点】正弦函数的图象,正弦函数的单调性,由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【分析】(1_???é??????????????_象得到函数的最大值和最小值,求出 值,根据周期得到 ,把 代入解析式得到 ,从而得到 ,再求对称中心即可.(2)首先根据图象变换得到 ,再求单调区间和最值即可.
28.【答案】 解:(Ⅰ)
.
所以 的最小正周期为 .
令 ,得 ( ).
所以 的单调递增区间为 ( ).
(Ⅱ)由(Ⅰ)知 ,
所以 .
由 ,得 或 .
当 时, .
当且仅当 ,即 时, .
所以 仅有一个根,因为 , ,
所以 的取值范围是 .
【考点】函数y=Asin(ωx+φ)的图象变换,复合三角函数的单调性
【解析】【分析_?????????????????¨_两角差的余弦公式、二倍角公式和辅助角公式对函数化简,利用公式 求最小正周期,利用正弦函数的图像性质列不等式求单调增区间.(Ⅱ)通过伸缩和平移变换,求 ,解方程,转化为 与 仅有一个交点问题,进而求出 的取值范围.
29.【答案】 (1)解:
,
所以,函数 的最小正周期为 ;
(2)解:将函数 的图象右移 个单位,
得到函数 的图象,
由 ,解得: .
函数 的单调递增区间为 .
【考点】三角函数中的恒等变换应用,正弦函数的单调性,函数y=Asin(ωx+φ)的图象变换,正弦函数的周期性
【解析】【分析】(1)利用三角_??????????????????_化简函数 的解析式为 ,利用正弦型函数的周期公式可求得函数 的最小正周期;(2)利用三角函数图象变换规律得出 ,然后解不等式 ,可得函数 的单调递增区间.
30.【答案】 (1)解:由图得 ,
因为 为函数递增区间上的零点,
所以 ,即 .
因为 ,所以 ,
即 ,
将函数 的图象上所有点的横坐标伸长到原来的4倍(纵坐标不变),再将所得图象向左平移 个单位长度可得 ;
(2)解:因为 ,所以 ,
所以当 时, 取最小值 ,
当 时, 取最大值1,
因为 恒成立,即 恒成立,
所以 ,
即 .
【考点】函数恒成立问题,函数y=Asin(ωx+φ)的图象变换,由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【分析】(1)先根据 的解析式;再结合图象变化规律说明 的图象怎样经过2次变换得到 的图象;(2)先结合正弦函数的性质求出 的范围;再结合恒成立问题即可求解.
5.6 函数 y=Asin( ωx + φ)
一、单选题(共10题;共20分)
1.把函数 图象上各点的横坐标缩短到原来的 倍(纵坐标不变),再将图象向右平移 个单位,得到函数 ,那么 的值为(?? )
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
2.要得到函数 的图像,只需要将函数 的图像(??? )
A.?向左平移 个单位?????B.?向右平移 个单位?????C.?向左平移 个单位?????D.?向右平移 个单位
3.已知函数 ( , , )的部分图象如图所示,若将函数 的图象向右平移 个单位后,得到一个偶函数的图象,则 的取值可能为(??? )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
4.函数 _????°???????è±????_每个点的纵坐标保持不变,横坐标扩大为原来的2倍,然后再将它的图形沿x轴向左平移 个单位,得到函数 的图象,则函数 的解析式是(?? ?)
A.????????????B.????????????C.????????????D.?
5.为了得到函数 的图像,只需将函数 的图像(??? )
A.?向右平移 个单位??????B.?向右平移 个单位??????C.?向左平移 个单位??????D.?向左平移 个单位2-1-c-n-j-y
6.函数 的图像可以由 的图像(??? )个单位得到.
A.?向左平移 ?????????????????????B.?向右平移 ?????????????????????C.?向左平移 ?????????????????????D.?向右平移
7.为了得到函数 的图象,可以将函数 的图象( ??)
A.?向右平移
B.?向左平移 个单位
C.?向右平移 个单位
D.?向左平移 个单位
8.为了得到函数 的图象,只需把函数 的图象(??? )
A.?向左平移 _?????????é???????_????????????????????????????????????B.?向左平移 个单位长度
C.?向右平移 个单位长度?????????????????????????????????????D.?向右平移 个单位长度
9.若 的最小值为-2,其图像相邻最高点与最低点横坐标之差为 ,且图像过点(0,1),则其解析式是( ??)
A.?????????????B.?????????????C.?????????????D.?
10.已知函数 的部分图象如下图所示,则函数 的解析式(????? )
A.??????????????????????????????????????????B.?
C.???????????????????????????????????????????D.?
二、填空题(共10题;共12分)
11.把函数 的图象向左平移 个单位,得到的函数是________.
12.若两个函数的图象经过若干次平移后能够重合,则称这两个函数为“同形”函数.给出下列三个函数: 21教育名师原创作品
① ;② ;③ .
其中,为“同形”函数的序号是________.
13.已知函数 ( , , )在半个周期内的图象如图所示,则 ________.
14.把函数 图象向右平移 个单位,得函数 ( )的图象,则 的值等于________.
15.函数 的部分图像如图所示.若 (点A为图像的一个最高点), ,则 ________, ________.
16.已知函数 的部分图象如图所示,则 的值为________.
?
17.将函数 的图象向左平移 个单位长度,若所得图象关于原点对称,则a的值为________. 【来源:21cnj*y.co*m】
18.关于函数 有下列命题:①函数 的周期为 ;②直线 是 的一条对称轴;③点 是 的图象的一个对称中心;④将 的图象向左平移 个单位,可得到 的图象;其中正确的序号是________.(把你认为正确的序号都写上)
19.已知函数 的部分图象如图所示,则 ________, ________.
20.设函数 (其中A, , 为常数且A>0, >0, )的部分图象如图所示,若 ( ),则 的值为________.
三、解答题(共10题;共95分)
21.已知函数 满足下列3个条件:
①函数 的周期为 ;② 是函数 的对称轴;③ .
(1)请任选其中二个条件,并求出此时函数 的解析式;
(2)若 ,求函数 的最值.
22.已知函数 的部分图象如图所示.
(1)求函数 的解析式;
(2)求函数 在区间 上的值域.
23.设 .
(1)求使不等式 成立的x的取值集合;
(2)先将 图象_????????????????¨?_坐标伸长为原来的2倍,纵坐标不变;再向右平移 个单位;最后向下平移 个单位得到函数 的图象.若不等式 在 上恒成立,求实数 的取值范围.
24.已知函数 的部分图象如图所示.
(1)求 的解析式;
(2)求 在 上的最大值和最小值.
25.已知函数 , .
(1)将函数 _?????????è?¨?¤????_ (其中 , , , )形式;
(2)用五点法列表并作出函数 一个周期内的图象.
?????? ? ? ? ? ?
????????? ? ? ? ? ?
???????? ? ? ? ? ?
26.已知函数 .
(1)求函数 的最小正周期;
(2)若将函数 每点的横坐标变为原来的2倍,纵坐标不变,得到函数 的图象,求 在区间 上的值域. 2·1·c·n·j·y
27.已知函数 的部分图像如图所示.
(1)求 的解析式及对称中心坐标;
(2)先将 __???????????????_标缩短到原来的 倍,再向右平移 个单位,最后将图像向上平移1个单位后得到 的图像,求函数 在 上的单调增区间和最值.
28.已知函数 .
(Ⅰ)求 的最小正周期和单调递增区间;
(Ⅱ)将函数 像上所有点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图像向左平移 个单位长度,得到函数 的图像,若关于 的方程 在 上恰有2个根,求 的取值范围.
29.已知函数 .
(1)求函数 的最小正周期;
(2)将函数 的图象右移 个单位得到 的图象,求函数 的单调递增区间.
30.已知函数 , 的部分图象如图所示.
(1)求 的解析式,并说明 的图象怎样经过2次变换得到 的图象;
(2)若对于任意的 ,不等式 恒成立,求实数 的取值范围.
答案解析部分
一、单选题
1.【答案】 B
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】把函 图象上各点的横坐标缩短到原来的 倍,得到的函数图象对应的解析式为 , 21·世纪*教育网
再将图象向右平移 ,得到 ,所以 .
故答案为:B.
【分析】先根据图象变换求出 ,然后代入可得 的值.
2.【答案】 B
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】解:函数 等价于 ,
故只需要将 向右平移 即可得到.
故答案为:B.
【分析】先将函数 转化为 ,然后根据平移的规则即可得出答案.
3.【答案】 D
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由函数图像可知,
而 ,所以
由周期公式可得
所以
将最低点坐标 代入解析式可知
则
所以
因为
所以当 时,
则解析式为
将解析式向右平移 单位后,可得
因为平移后的函数为偶函数,则
解得
对比四个选项,当 时,
故答案为:D
【分析】根据部分函数图像,先求得函数解析式.结合函数平移变化,求得平移后的解析式,由平移后为偶函数并对比选项即可求解.【来源:21·世纪·教育·网】
4.【答案】 C
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】解:由题意曲 的图象沿x轴向右平移 个单位,再纵坐标不变,横坐标缩小为原来的一半即可得到 的图形,故 21*cnjy*com
的图形沿x轴向右平移 个单位所得图形对应的函数解析式为 ,然后再将所得的曲线上的点的纵坐标保持不变,横坐标缩小到原来的一半,所得的图形对应的解析式为
故答案为:C.
【分析】此类题_????????????è?????_通过反变求出原来函数的解析式,由题意可由曲线与 的图形沿x轴向右平移 个单位,再纵坐标不变,横坐标缩小为原来的一半即可得到 的解析式,选出正确选项
5.【答案】 A
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】根据函数平移变换,由 变换为 ,
只需将 的图象向右平移 个单位,即可得到 的图像,
故答案为:A.
【分析】根据函数平移变换的方法,由 即 ,只需向右平移 个单位即可.
6.【答案】 D
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】因为 ,
所以只需由 的图像向右平移 个单位得到.
故答案为:D
【分析】由 ,可以确定函数图象之间的变换,即可求解.
7.【答案】 D
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答_??????é??è????????_数图像平移变换:函数 的图像平移 单位( ,向左; ,向右)所得图像对应函数为 , 【出处:21教育名师】
将函数 的图象平移 个单位后,所得图像对应函数为
;令 ,得 ,
故答案为:D。
【分析】利用已知条件_?????????è§???????_数的图象变换,从而将函数 的图象向左平移 个单位得到函数 的图象。【版权所有:21教育】
8.【答案】 B
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答 向左平移 单位可得 ,
故答案为:B.
【分析】对比两个函数中自变量x的变化情况,再结合“左加右减”的平移原则,即可得答案;
9.【答案】 C
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由已知_???????????????A_=2,T=2× = ,故 ,又因为图像过点(0,1),所以2 =1,可得 ,所以 ,
故答案为:C.
【分析】利用三角型函数的最_?°???????-2???_从而求出A的值,再利用三角型函数图象相邻最高点与最低点横坐标之差为 ,从而结合最小正周期公式求出的值,再利用三角型函数图象过点(0,1)结合正弦函数图象点对应法,从而求出的值,从而求出三角型函数的解析式。
10.【答案】 D
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由函_??°??????è±????__
即 则 ,
则 ,
则 则
则
∵ ,∴当k=0时,
则函数 .
故答案为:D.
【分析】根据函数的图象求出A,ω 和φ的值即可.
二、填空题
11.【答案】
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】把函数 的图象向左平移 个单位,
得到的函数是 ,
故答案为 .
【分析】直接利用三角函数图象的平移变换法则求解即可.
12.【答案】 ①③
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】根据“同形”函数的定义可知,若两个函数互为“同形”函数,则两个函数的振幅相等,最小正周期也相等, www-2-1-cnjy-com
对于①中的函数 ,该函数的振幅为 ,最小正周期为 ;
对于②中的函数 ,该函数的振幅为 ,最小正周期为 ;
对于③中的函数 ,该函数的振幅为 ,最小正周期为 .
将函数 的图象向右平移 个单位长度可得到函数 的图象.
因此,为“同形”函数的序号是①③.
故答案为:①③.
【分析】将①③中的函数解析式化简,根据“同形”函数的定义可知,两个函数的振幅相等,最小正周期也相等,由此可得出结论.
13.【答案】
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】根据 的图象可知 ,
,
所以 .
由 得 ,由于 ,即 ,
,所以 .
故答案为:
【分析】根据 的图象,依次求得 和 的值.
14.【答案】
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】把函数 的图象向右平移 个单位,
所得图象对应的解析式为 ,
由题设可知 对任意的 恒成立,
故 对任意的 恒成立,
所以 ,故 即 ,
因为 ,故 ,
故答案为: .
【分析】先求出 的图象平移后所得图象对应的解析式,再利用该解析式与 完全一致可求 的值.www.21-cn-jy.com
15.【答案】 ;
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】解:因为点 为图像的一个最高点,所以 ,
由图可知, ,得 ,
所以 ,解得 ,
所以 ,
将点 坐标代入 中,得 ,
所以 , ,
因为 ,所以 ,
故答案为: ;
【分析】由点 图像的一个最高点,可求出振幅 ,再由 , 可求出周期,从而可求出 的值,然后代入其中的一个点的坐标可求出 的值.
16.【答案】
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由图可得: , 或
由于0在函数 的单调减区间内,
所以 .
故答案为:
【分析】根据图像可得 ,根据0所在位置,处于函数的单调减区间,即可得解.
17.【答案】
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】将函数 的图象向左平移 个单位长度,得解析式为 ,它的图象关于原点对称,则 ,即 , , 21教育网
故答案为: .
【分析】求出平移后的函数解析式,由新函数图象过原点得出 ,
18.【答案】 ①③
【考点】三角函数的周期性及其求法,正弦函数的奇偶性与对称性,函数y=Asin(ωx+φ)的图象变换 21*cnjy*com
【解析】【解答】 ,则函数周期为 ;当 时 ,故 不是函数的对称轴;当 时, ,故点 是 的图象的一个对称中心;将 的图象向左平移 个单位,
得到 。
故答案为:①③
【分析】化简得到 ,计算函数的周期,对称轴,对称中心,平移依次判断每个选项得到答案.
19.【答案】 2;
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由图像知道函数_????????¨??????__ ,故周期为 将函数零点代入得到 由题意可知 ,故得到 。
故答案为: ;? 。
【分析】利用三角型函数的_é?¨????????°???è±?_结合最小正周期公式和特殊点代入法,再利用正弦函数的五点对应法,从而求出函数 的解析式,从而求出的值。
20.【答案】
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】由函数 的图知, ,由 ,得 ,
∴ ,
又 ,且 ,∴ ,∴ ,
由 ,∴ ,
又 ,∴ ,
∴ ,
∴
? ?
故答案为 .
【分析】由函数 _??????è±??±????A_、T、 和 的值,写出 的解析式,再由 的值,利用三角恒等变换求出 的值.21cnjy.com
三、解答题
21.【答案】 (1)解:选①②,则 ,解得 ,
因为 ,所以 ,即 ;
选①③, ,由 得 ,
因为 ,所以 ,即 ;
选②③, ,由 得 ,
因为 ,所以 ,即
(2)解:由题意得,因为 ,所以 .
所以当 即 时, 有最大值 ,
所以当 即 时, 有最小值 .
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【分析】(1) ,由②知 ,由③知 ,结合 即可求出 的解析式.(2)由 可得 ,进而可求出函数最值.
22.【答案】 (1)解:由图可知 ,解得
解得
又函数过点
即 , 解得
, ,
(2)解:
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【分_?????????1?????±_图可知 即可求出 ,再根据函数的最小正周期求出 ,又函数过点 ,代入即可求出 从而得到函数解析式;(2)由x的取值范围求出 的范围,再由余弦函数的性质解答.21世纪教育网版权所有
23.【答案】 (1) .
即:
,
所以原不等式的解集为:
(2)解: 将图象上所有点的横坐标伸长为原来的2倍,纵坐标不变,得 ;再向右平移 个单位,得 ;最后向下平移 个单位得到函数 ,
∴ .
设 ,由 可得: ,
则原不等式等价于: 在 上恒成立;
设 , ,则 在 递增,在 递减,所以 ,
所以
【考点】函数恒成立问题,正弦函数的图象,函数y=Asin(ωx+φ)的图象变换
【解析】【分析】(1)利用_é??????????????è??_助角公式可得 ,因此 等价于 ,利用正弦函数的性质可求不等式的解集.(2)根据图象变换可得 ,从而原不等式可化为 在 ,换元后利用二次函数的性质可求 的取值范围.
24.【答案】 (1)解:由图可知 ,
,则 ,
将 代入 得 ,则 .?
因为 ,所以 .
故
(2)解:由 ,得 .
当 即 时, 取得最大值,且 ;
当 ,即 时, 取得最小值,且
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的最值
【解析】【分析】(_1?????±????¤§???_确定A,由周期确定 ,由点的坐标确定 ;(2)求出 的范围,再根据正弦函数的性质得最值.
25.【答案】 (1)解:
(2)解:列表如下:
x
y 0
0 - 0
图象如图所示:
【考点】三角函数中的恒等变换应用,五点法作函数y=Asin(ωx+φ)的图象
【解析】【分析】(1)利用_é??????????????è??_助角公式可求得 .(2)先完善表格,再依据各点绘制一个周期内的图象.
26.【答案】 (1)解:由题可知:
所以
则
所以
所以最小正周期
(2)解:由(1)可知: ,
依题变换之后
由 ,所以
所以
所以 在区间 上的值域为
【考点】三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的定义域和值域,函数y=Asin(ωx+φ)的图象变换 21·cn·jy·com
【解析】【分析】(1)根据两_è§????????·???????_弦、余弦公式并结合辅助角公式化简可得 ,然后根据周期公式简单计算可得结果.(2)根据(1)的条件,以及伸缩变换可得 ,然后使用整体法以及正弦型函数的性质可得结果.
27.【答案】 (1)解:由图知: ,解得 , ,
, 所以 ,
把点 代入得: ,
即 , ,又因为 ,所以 ,
即 ;
令 , ,解得 ,
故所求对称中心坐标为: , .
(2)解: 的图像纵坐标缩短到原来的 倍,得到 ,
再向右平移 个_??????????????°__ ,
再将图像向上平移1个单位,得到
由 , ,
解得 ,
因为 ,所以增区间为 .
因为 ,当 时, 有最大值 ,
当 时, 有最小值 .
【考点】正弦函数的图象,正弦函数的单调性,由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【分析】(1_???é??????????????_象得到函数的最大值和最小值,求出 值,根据周期得到 ,把 代入解析式得到 ,从而得到 ,再求对称中心即可.(2)首先根据图象变换得到 ,再求单调区间和最值即可.
28.【答案】 解:(Ⅰ)
.
所以 的最小正周期为 .
令 ,得 ( ).
所以 的单调递增区间为 ( ).
(Ⅱ)由(Ⅰ)知 ,
所以 .
由 ,得 或 .
当 时, .
当且仅当 ,即 时, .
所以 仅有一个根,因为 , ,
所以 的取值范围是 .
【考点】函数y=Asin(ωx+φ)的图象变换,复合三角函数的单调性
【解析】【分析_?????????????????¨_两角差的余弦公式、二倍角公式和辅助角公式对函数化简,利用公式 求最小正周期,利用正弦函数的图像性质列不等式求单调增区间.(Ⅱ)通过伸缩和平移变换,求 ,解方程,转化为 与 仅有一个交点问题,进而求出 的取值范围.
29.【答案】 (1)解:
,
所以,函数 的最小正周期为 ;
(2)解:将函数 的图象右移 个单位,
得到函数 的图象,
由 ,解得: .
函数 的单调递增区间为 .
【考点】三角函数中的恒等变换应用,正弦函数的单调性,函数y=Asin(ωx+φ)的图象变换,正弦函数的周期性
【解析】【分析】(1)利用三角_??????????????????_化简函数 的解析式为 ,利用正弦型函数的周期公式可求得函数 的最小正周期;(2)利用三角函数图象变换规律得出 ,然后解不等式 ,可得函数 的单调递增区间.
30.【答案】 (1)解:由图得 ,
因为 为函数递增区间上的零点,
所以 ,即 .
因为 ,所以 ,
即 ,
将函数 的图象上所有点的横坐标伸长到原来的4倍(纵坐标不变),再将所得图象向左平移 个单位长度可得 ;
(2)解:因为 ,所以 ,
所以当 时, 取最小值 ,
当 时, 取最大值1,
因为 恒成立,即 恒成立,
所以 ,
即 .
【考点】函数恒成立问题,函数y=Asin(ωx+φ)的图象变换,由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【分析】(1)先根据 的解析式;再结合图象变化规律说明 的图象怎样经过2次变换得到 的图象;(2)先结合正弦函数的性质求出 的范围;再结合恒成立问题即可求解.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
