苏教版三上数学 1.6笔算两、三位数乘一位数(不进位) 教案
文档属性
| 名称 | 苏教版三上数学 1.6笔算两、三位数乘一位数(不进位) 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 05:34:10 | ||
图片预览


文档简介
笔算两、三位数乘一位数(不进位)教学设计
【教学内容】
苏教版三年级上册第11页例5及相关练习。
【教学目标】
1. 经历探索两位数乘一位数的笔算过程,理解并掌握两、三位数乘一位数(不进位)的笔算方法,能正确笔算两、三位数乘一位数(不进位)。
2. 在具体情境中学习两、三位数乘一位数(不进位)的笔算方法,理解笔算的算理,能正确算出结果,解决相应的实际问题,并能根据算法推算出算式中相应的数。
3. 经历与同学交流算法的过程,培养自主探索、合作交流的意识,体会乘法竖式的简洁性。
【教学重点】
掌握两、三位数乘一位数(不进位)的笔算方法。
【教学难点】
理解两、三位数乘一位数(不进位)的笔算算理。
【学具】
每个学生准备36根小棒图(3捆,每捆10根;单个的6根),一份学习单。
【教学过程】
主动探索,学会笔算
(一) 两位数乘一位数
1.(出示例题图)提问:从图中你知道什么?(生:湖面上飞过3队大雁,每队12只。)
2. 你能提出一个用乘法计算的问题吗?(生:一共有多少只?)
怎么列式?(生:算式是12×3或者3×12。)板书:12×3。
设计意图:从具体情境入手,激发学生学习兴趣和探究欲望,调动了学生的生活经验。同时,本环节还培养学生分析问题、发现问题、提出问题的能力。
3. 你准备怎样算出12×3的积呢?
(出示探索一)请一个小朋友大声读一遍要求。
要求:
(1)先用小棒图摆一摆;
(2)再画一画、写一写、算一算,把你的想法记录在学习单上。
生尝试探究算法。师巡视选取作品展示交流。
预设:
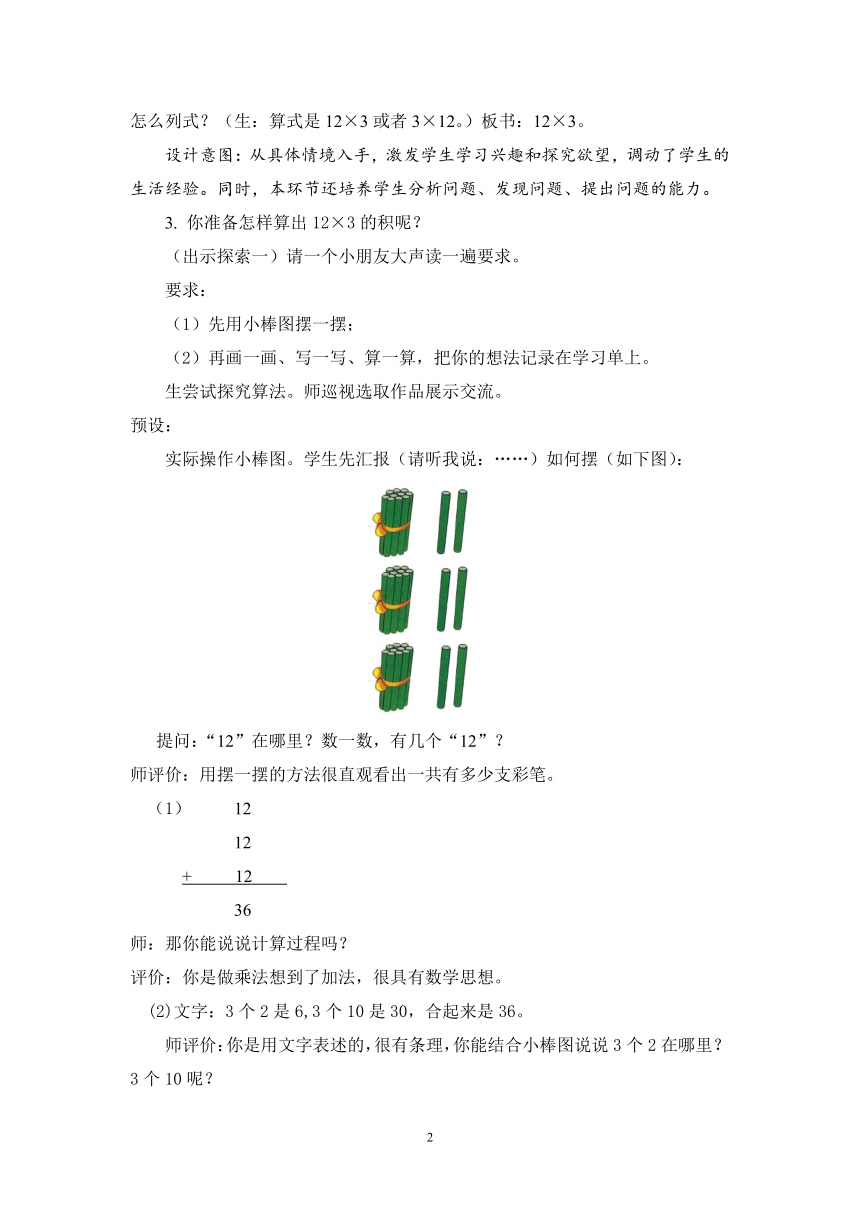
实际操作小棒图。学生先汇报(请听我说:……)如何摆(如下图):
提问:“12”在哪里?数一数,有几个“12”?
师评价:用摆一摆的方法很直观看出一共有多少支彩笔。
(1) 12
12
+ 12
36
师:那你能说说计算过程吗?
评价:你是做乘法想到了加法,很具有数学思想。
(2)文字:3个2是6,3个10是30,合起来是36。
师评价:你是用文字表述的,很有条理,你能结合小棒图说说3个2在哪里?3个10呢?
师:对比1、2号作品,它们之间有联系吗?(生:有,第一种方法是把3个12依次相加;第二种是先算个位上3个2相加,再算十位上3个10相加,合起来是36。)
(3)算式:2×3=6,10×3=30, 6+30=36。
师评价:你们读懂3号作品了吗?
对比2、3号作品:3号其实是把2号的方法用算式来表示。
对比1、2、3号作品:认真看一看这三个作品,哪个作品更简洁?
老师把这幅作品请到黑板上。
师:3号作品创作者,你能用黑板上的小棒,实际操作你的想法吗?(能)
师评价:列式计算,分步表达了计算过程,真清楚!
师:我们看,他是分几步算的?
生:分了3步算的。先算3个2是6,再算3个10是30,最后算6+30=36。
师评价:你真有一双善于发现的眼睛!像这样的两位数乘一位数的计算,我们一般把两位数分成个位和十位两部分,依次乘一位数,再求和。(一边说一边做手势,指着3个2,和3个10。)
师:请你把3号的计算过程和同桌说一说。
设计意图:乘法竖式教学,不光要讲方法,还要讲道理,更要鼓励学生去探索和发现。因此,就“笔算两、三位数乘一位数(不进位)”的教学而言,我们既要告诉学生标准的算法,还应当让学生明白这样算的道理。如果能引导学生“创造”乘法竖式的写法,将会激发学生的创造力,让学生更好地学习数学。因此,需要运用几何直观,明确计算步骤。
笔算两位数乘一位数(不进位)时,先用一位数与两位数个位上的数相乘,乘得的积写在个位上;再用一位数乘两位数十位上的数,乘得的积写在十位上。算法比较抽象。小学三年级的学生以直观形象思维为主,抽象概括能力较弱。实际的算理是这样的:比如12×3,表示3个12相加。因此要先算3个2相加;再算3个10相加;然后合起来。而在乘法竖式中,因为“位置值”的存在,“合起来”的这一步也就省去了。如果借助小棒图进行实际操作,这种抽象的算法就会直观地呈现出来。
探索竖式的写法。
(1)(出示探索二)现在,你能根据口算过程尝试用竖式清晰记录计算步骤吗?拿出学习单,独立完成探索二。
学生尝试竖式计算。
选取作品展示交流。
1号竖式:
大家看,1号同学笔算12×3用这三个竖式来计算,是把哪三个横式写成了竖式?(生:把“2×3=6,10×3=30, 6+30=36”这三个横式写成了竖式)。你有什么想评价的吗?
学生汇报:写三个竖式很麻烦,太费时间。
老师提出新的要求:能不能想办法把它们合并在一个竖式里?
对比2号、3号竖式:
质疑:新的竖式中有“2×3=6,10×3=30, 6+30=36”这三步吗?在哪里?谁给大家说说?这两个竖式有什么不同?(生:左边的竖式写了“+”,右边的竖式没写。)
“+”能不能省去不写?(生:能。因为写“+”表示求和,“+”省去不写,大家也明白最后算的是加法,所以“+”可以省去。)
还有一个数字可以省去不写,你知道吗?
4号竖式:
师:当算到3和1个十相乘时,就在竖式中写“3”和“6”对齐,这样写行吗?为什么?(生:不行。因为这里的“3”代表“3个十”,如果和“6”对齐,就不是“3个十”了,所以,“3”不能和“6”对齐,“3”要写在十位上,要和十位对齐。)
提问:竖式中有“2×3=6,10×3=30, 6+30=36”这三步吗,在哪里?
为什么30里面的“0”可以省去不写?(生:因为“3”写在十位上,就能代表30,所以“0”可以省去不写。)
说明:第二步算10×3 = 30,可以看成1(个十)×3=3(个十),所以“0”省去不写。但是,“3”必须写在十位上。这样就把“两位数乘一位数”变成了两次“一位数乘一位数”,一次是2×3,另一次是1(个十)×3,方便了同学们口算。
今天是我们第一次学习两位数乘一位数的竖式计算,现在刘老师把4号竖式规范的写在黑板上。
问:我们一起看,这道竖式能清楚地记录我们计算过程吗?你知道竖式每一步对应的小棒和横式在哪里吗?谁上来找一找。
这里的“6”对应小棒在哪里?“3”呢?
请同学们修改完善自己的作品。
自己看着竖式说一说计算过程,谁想说给大家听?指1名说竖式计算过程,同桌互说。
(2)再次探索
师:这个竖式还能再简写吗?
5号竖式:
提问:在这个竖式中,还有“2×3=6,10×3=30, 6+30=36”这三步吗,在哪里?
对比4号、5号作品:你觉得哪个写法比较简洁?
以后我们在笔算乘法时,就可以像5号同学这样写。板书简便竖式。
概括乘法竖式计算方法。
问:谁能看着这个简便竖式说说乘法竖式的计算方法?(生:先用一位数乘两位数个位上的数,乘得的积写在个位上;再用一位数乘两位数十位上的数,乘得的积写在十位上。)同桌互相说。这题是解决问题还要写答。
设计意图:根据“2×3=6,10×3=30, 6+30=36”这三步,要求学生探究乘法竖式的写法,并不断追问,乘法竖式中这三步在哪里,逐步让学生明晰竖式计算的道理。在此基础上抽象概括乘法竖式的计算方法就水到渠成。
(二)三位数乘一位数
谈话:你能借鉴刚刚研究的两位数乘一位数的笔算方法,摆竖式计算3×312吗?
出示我尝试活动要求:①想:这次计算分几步;②算:积的百位上写几;③说:和同桌说一说自己的想法。
学生独立尝试。
指名介绍竖式计算过程。
出示错例,生点评反思。关注竖式计算格式。
指出:用竖式计算乘法时一般把数位多的乘数写在上面。
小结:三位数乘一位数怎么算?(用三位数个位、十位、百位上的数依次乘一位数。)
揭示课题:今天我们一起学习了什么内容?(笔算两、三位数乘一位数)观察这两道竖式,有什么共同的地方?(都没有进位)板书:不进位。
师:今天我们一起学了不进位的笔算乘法,当然还有进位的笔算乘法, 期待下节课的研究。
二、巩固练习,形成技能
1. 我练习:先说一说乘的顺序,再计算。
3 23 123
× 2 × 3 × 2
2. 我练习:解决问题。
运动场的看台每个区有342个座位,2个区最多可以坐多少人?
3. 我练习:拓展练习。
三、全课总结,交流收获
通过今天的学习,你有什么收获?
【板书设计】
笔算两、三位数乘一位数(不进位)
12×3=36(只) 3×312=936
答:一共有36只。
【教学内容】
苏教版三年级上册第11页例5及相关练习。
【教学目标】
1. 经历探索两位数乘一位数的笔算过程,理解并掌握两、三位数乘一位数(不进位)的笔算方法,能正确笔算两、三位数乘一位数(不进位)。
2. 在具体情境中学习两、三位数乘一位数(不进位)的笔算方法,理解笔算的算理,能正确算出结果,解决相应的实际问题,并能根据算法推算出算式中相应的数。
3. 经历与同学交流算法的过程,培养自主探索、合作交流的意识,体会乘法竖式的简洁性。
【教学重点】
掌握两、三位数乘一位数(不进位)的笔算方法。
【教学难点】
理解两、三位数乘一位数(不进位)的笔算算理。
【学具】
每个学生准备36根小棒图(3捆,每捆10根;单个的6根),一份学习单。
【教学过程】
主动探索,学会笔算
(一) 两位数乘一位数
1.(出示例题图)提问:从图中你知道什么?(生:湖面上飞过3队大雁,每队12只。)
2. 你能提出一个用乘法计算的问题吗?(生:一共有多少只?)
怎么列式?(生:算式是12×3或者3×12。)板书:12×3。
设计意图:从具体情境入手,激发学生学习兴趣和探究欲望,调动了学生的生活经验。同时,本环节还培养学生分析问题、发现问题、提出问题的能力。
3. 你准备怎样算出12×3的积呢?
(出示探索一)请一个小朋友大声读一遍要求。
要求:
(1)先用小棒图摆一摆;
(2)再画一画、写一写、算一算,把你的想法记录在学习单上。
生尝试探究算法。师巡视选取作品展示交流。
预设:
实际操作小棒图。学生先汇报(请听我说:……)如何摆(如下图):
提问:“12”在哪里?数一数,有几个“12”?
师评价:用摆一摆的方法很直观看出一共有多少支彩笔。
(1) 12
12
+ 12
36
师:那你能说说计算过程吗?
评价:你是做乘法想到了加法,很具有数学思想。
(2)文字:3个2是6,3个10是30,合起来是36。
师评价:你是用文字表述的,很有条理,你能结合小棒图说说3个2在哪里?3个10呢?
师:对比1、2号作品,它们之间有联系吗?(生:有,第一种方法是把3个12依次相加;第二种是先算个位上3个2相加,再算十位上3个10相加,合起来是36。)
(3)算式:2×3=6,10×3=30, 6+30=36。
师评价:你们读懂3号作品了吗?
对比2、3号作品:3号其实是把2号的方法用算式来表示。
对比1、2、3号作品:认真看一看这三个作品,哪个作品更简洁?
老师把这幅作品请到黑板上。
师:3号作品创作者,你能用黑板上的小棒,实际操作你的想法吗?(能)
师评价:列式计算,分步表达了计算过程,真清楚!
师:我们看,他是分几步算的?
生:分了3步算的。先算3个2是6,再算3个10是30,最后算6+30=36。
师评价:你真有一双善于发现的眼睛!像这样的两位数乘一位数的计算,我们一般把两位数分成个位和十位两部分,依次乘一位数,再求和。(一边说一边做手势,指着3个2,和3个10。)
师:请你把3号的计算过程和同桌说一说。
设计意图:乘法竖式教学,不光要讲方法,还要讲道理,更要鼓励学生去探索和发现。因此,就“笔算两、三位数乘一位数(不进位)”的教学而言,我们既要告诉学生标准的算法,还应当让学生明白这样算的道理。如果能引导学生“创造”乘法竖式的写法,将会激发学生的创造力,让学生更好地学习数学。因此,需要运用几何直观,明确计算步骤。
笔算两位数乘一位数(不进位)时,先用一位数与两位数个位上的数相乘,乘得的积写在个位上;再用一位数乘两位数十位上的数,乘得的积写在十位上。算法比较抽象。小学三年级的学生以直观形象思维为主,抽象概括能力较弱。实际的算理是这样的:比如12×3,表示3个12相加。因此要先算3个2相加;再算3个10相加;然后合起来。而在乘法竖式中,因为“位置值”的存在,“合起来”的这一步也就省去了。如果借助小棒图进行实际操作,这种抽象的算法就会直观地呈现出来。
探索竖式的写法。
(1)(出示探索二)现在,你能根据口算过程尝试用竖式清晰记录计算步骤吗?拿出学习单,独立完成探索二。
学生尝试竖式计算。
选取作品展示交流。
1号竖式:
大家看,1号同学笔算12×3用这三个竖式来计算,是把哪三个横式写成了竖式?(生:把“2×3=6,10×3=30, 6+30=36”这三个横式写成了竖式)。你有什么想评价的吗?
学生汇报:写三个竖式很麻烦,太费时间。
老师提出新的要求:能不能想办法把它们合并在一个竖式里?
对比2号、3号竖式:
质疑:新的竖式中有“2×3=6,10×3=30, 6+30=36”这三步吗?在哪里?谁给大家说说?这两个竖式有什么不同?(生:左边的竖式写了“+”,右边的竖式没写。)
“+”能不能省去不写?(生:能。因为写“+”表示求和,“+”省去不写,大家也明白最后算的是加法,所以“+”可以省去。)
还有一个数字可以省去不写,你知道吗?
4号竖式:
师:当算到3和1个十相乘时,就在竖式中写“3”和“6”对齐,这样写行吗?为什么?(生:不行。因为这里的“3”代表“3个十”,如果和“6”对齐,就不是“3个十”了,所以,“3”不能和“6”对齐,“3”要写在十位上,要和十位对齐。)
提问:竖式中有“2×3=6,10×3=30, 6+30=36”这三步吗,在哪里?
为什么30里面的“0”可以省去不写?(生:因为“3”写在十位上,就能代表30,所以“0”可以省去不写。)
说明:第二步算10×3 = 30,可以看成1(个十)×3=3(个十),所以“0”省去不写。但是,“3”必须写在十位上。这样就把“两位数乘一位数”变成了两次“一位数乘一位数”,一次是2×3,另一次是1(个十)×3,方便了同学们口算。
今天是我们第一次学习两位数乘一位数的竖式计算,现在刘老师把4号竖式规范的写在黑板上。
问:我们一起看,这道竖式能清楚地记录我们计算过程吗?你知道竖式每一步对应的小棒和横式在哪里吗?谁上来找一找。
这里的“6”对应小棒在哪里?“3”呢?
请同学们修改完善自己的作品。
自己看着竖式说一说计算过程,谁想说给大家听?指1名说竖式计算过程,同桌互说。
(2)再次探索
师:这个竖式还能再简写吗?
5号竖式:
提问:在这个竖式中,还有“2×3=6,10×3=30, 6+30=36”这三步吗,在哪里?
对比4号、5号作品:你觉得哪个写法比较简洁?
以后我们在笔算乘法时,就可以像5号同学这样写。板书简便竖式。
概括乘法竖式计算方法。
问:谁能看着这个简便竖式说说乘法竖式的计算方法?(生:先用一位数乘两位数个位上的数,乘得的积写在个位上;再用一位数乘两位数十位上的数,乘得的积写在十位上。)同桌互相说。这题是解决问题还要写答。
设计意图:根据“2×3=6,10×3=30, 6+30=36”这三步,要求学生探究乘法竖式的写法,并不断追问,乘法竖式中这三步在哪里,逐步让学生明晰竖式计算的道理。在此基础上抽象概括乘法竖式的计算方法就水到渠成。
(二)三位数乘一位数
谈话:你能借鉴刚刚研究的两位数乘一位数的笔算方法,摆竖式计算3×312吗?
出示我尝试活动要求:①想:这次计算分几步;②算:积的百位上写几;③说:和同桌说一说自己的想法。
学生独立尝试。
指名介绍竖式计算过程。
出示错例,生点评反思。关注竖式计算格式。
指出:用竖式计算乘法时一般把数位多的乘数写在上面。
小结:三位数乘一位数怎么算?(用三位数个位、十位、百位上的数依次乘一位数。)
揭示课题:今天我们一起学习了什么内容?(笔算两、三位数乘一位数)观察这两道竖式,有什么共同的地方?(都没有进位)板书:不进位。
师:今天我们一起学了不进位的笔算乘法,当然还有进位的笔算乘法, 期待下节课的研究。
二、巩固练习,形成技能
1. 我练习:先说一说乘的顺序,再计算。
3 23 123
× 2 × 3 × 2
2. 我练习:解决问题。
运动场的看台每个区有342个座位,2个区最多可以坐多少人?
3. 我练习:拓展练习。
三、全课总结,交流收获
通过今天的学习,你有什么收获?
【板书设计】
笔算两、三位数乘一位数(不进位)
12×3=36(只) 3×312=936
答:一共有36只。
同课章节目录
- 一 两、三位数乘一位数
- 整十、整百数乘一位数的口算
- 倍的认识和有关倍的简单实际问题
- 两、三位数乘一位数(不进位)的笔算
- 两、三位数乘一位数(进位)的笔算
- 两、三位数乘一位数(连续进位)的笔算
- 乘数中间、末尾有0的乘法
- 二 千克和克
- 认识千克
- 认识克
- 三 长方形和正方形
- 长方形和正方形的基本特征
- 认识周长
- 长方形和正方形周长的计算
- 周长是多少
- 四 两、三位数除以一位数
- 两、三位数除以一位数的口算
- 两、三位数除以一位数(首位能整除)的笔算
- 除法的验算
- 两、三位数除以一位数(首位不能整除)的笔算
- 商中间、末尾有0的除法
- 五 解决问题的策略
- 间隔排列
- 六 平移、旋转和轴对称
- 七 分数的初步认识(一)
- 多彩的“分数条”
