湘教版(2012)初中数学七年级上册 3.1 建立一元一次方程模型 教案
文档属性
| 名称 | 湘教版(2012)初中数学七年级上册 3.1 建立一元一次方程模型 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 114.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 00:00:00 | ||
图片预览


文档简介
3.1建立一元一次方程模型(教案)
所用教材:湘教版初中数学七年级上册第83页。
教学目标:
1、借助高铁的现实情境,经历“把实际问题抽象为方程”的过程,体会方程是刻画现实世界数量关系的有效模型,培养观察、归纳、抽象、概括等能力。感受数学与生活的联系,增强学习数学的信心和民族自豪感。
2、经历方程、一元一次方程概念形成过程,体验从特殊到一般、分类思想。能识别方程、一元一次方程。会检验一个数是不是方程的解。
重点:一元一次方程概念的形成。
难点:建立方程模型,检验一个数是不是方程的解。
教学方法:问题导学、动手实践、交流讨论。
教学过程:一、情境导入
[提问]同学们坐过高速列车吗?你知道高速列车的平均速度大约是多少?
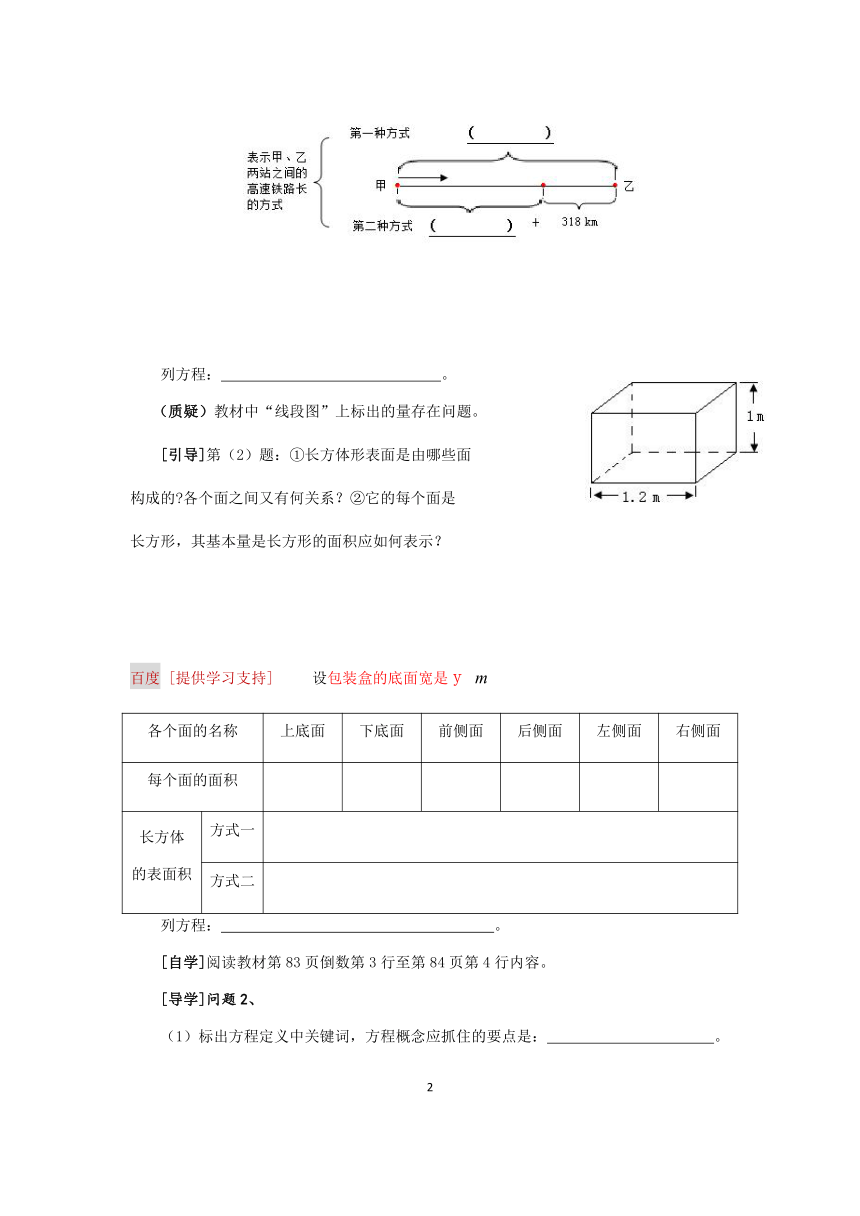
问题1、(1)甲、乙两站之间的高速铁路长1068,“和谐号”高速列车的平均速度为300/,则高速列车从甲站开往乙站需要多少时间?(用两种不同的方法求解)
(2)在小学已学过简易方程,请写出不同形式的2个简易方程:
、
。
[学生独立完成,各组代表在班上交流,教师用多媒体演示]`
二、引导探究
1、方程的概念
【构建模型】[独学]独立思考,用列方程的方法求解教材第83页“动脑筋”题。
问题1、(1)教材第83页动脑筋第(1)题。(2)教材第83页动脑筋第(2)题。
[学法指导](1)阅读题目,①熟悉背景,明确问题。这是什么问题?这个问题中基本量之间的关系是什么?
②进行标记,在题中划出关键的字、词、句。
(2)运用图表,建立关系。如“线段图、表格式”,抓入“列方程的本质是,从两个角度(也就是用两种方式)表示同一对象”(即等量关系)。
[引导]第(1)题:这是行程问题,其基本量(路程、速度、时间)的关系是什么?
用“线段图”进行分析。设
。
百度
[提供学习支持]
列方程:
。
(质疑)教材中“线段图”上标出的量存在问题。
[引导]第(2)题:①长方体形表面是由哪些面
构成的?各个面之间又有何关系?②它的每个面是
长方形,其基本量是长方形的面积应如何表示?
百度
[提供学习支持]
设包装盒的底面宽是y
各个面的名称
上底面
下底面
前侧面
后侧面
左侧面
右侧面
每个面的面积
长方体
的表面积
方式一
方式二
列方程:
。
[自学]阅读教材第83页倒数第3行至第84页第4行内容。
[导学]问题2、
(1)标出方程定义中关键词,方程概念应抓住的要点是:
。
(2)前面所列出的3个方程:300=1068,2.5+318=1068,2.4+2+2.4=6.8中,
所含的未知数分别是
、
、
。
从未知数的角度出发,你再举几个与上述方程形式不同的方程:
,它们所含未知数分别是:
。
(教师巡视指导,捕捉亮点与问题)
[交流]各组代表展示,教师有多媒体演示。
[讲解]反思“建立方程”过程,构建思维框架:[教师边讲边板书]
【变式训练】
问题3、(1)下列各式中,属于方程的是(
)
A.
B.
>1
C.
25+3=28
D.
2+1=3
(2)教材第85页第4行第3题
2、一元一次方程的定义
在前面学习中,我们得到了很多方程,把这些形形色色的方程放在一起,请各组合作学习,完成问题4。
问题4、观察下列方程,将它们按照自己设定的标准进行分类。
①300=1068,②
2.5+318=1068,③2.4+2+2.4=6.8,④,
⑤25=3.14,⑥+5=8,⑦,⑧.
[合学]各小组展开讨论,探究可能的分类方法,由代表在班上展示交流。
[点拨]可以围绕“未知数”分析。
[交流]可能的分类方法如下:
(1)按照未知数的个数进行分类:含一个未知数的有
,含有两个未知数的有
。
(2)按照未知数的次数进行分类:未知数次数为1次的有
,未知数次数为2的有
。
(3)既按照未知数的个数,又按照未知数的次数进行分类:未知数个数为1,并且未知数的次数是1的有
,其余的为一组。
我们把第(3)种分类方法得到的第一组方程叫一元一次方程。请同学们用自己的话说一说什么是“一元一次方程”。
[自学]阅读教材第84页的“一元一次方程的定义”,标出关键字、词。你再举几个一元一次方程的例子:
。
[讨论](1)你能说说“元”和“次”的具体含义。
(2)有学生说“2.4+2+2.4=6.8”不是一元一次方程?对吗?
【变式训练】问题5、
(1)下列方程中是一元一次方程的是(
)。
A.
B.
C.
D.
(2)若关于的方程2-3=1是一元一次方程,则=
。
3、方程的解
[练习]问题6、同学们在小学已学习了简易方程的解法,请求出下列方程中未知数的值
(1)+5=8,
(2)300=1068.
[讲解]方程的解的定义及说明。
(反思)对第84页“方程的解”,你是如何理解的?能举例子说明吗?
(提出问题)哪么如何检验未知数的值是不是方程的解呢?
[讨论]问题7、小明、小红同学分别求出问题6(1)、(2)的未知数的值分别是=3和=3.6后,为了判断结果是不是正确的,写出检验如下,请你判断其检验过程是否正确?
[质疑]阅读教材第84页,你认为这个验证过程是否存在问题?
【尝试练习】问题8、检验=2是不是方程2-6=7+4的解。[先独做,再由一名学生上台板书]
[讨论]检验未知数的值是不是方程的解有几个步骤?代入时应注意什么?
(归纳)检验方程的解的步骤
①代入:将未知数的值分别代入方程的左边和右边;
②计算:分别计算方程左边和右边的值;
③比较:比较左边和右边是不相等;
④判断:若相等,则是;若不相等,则不是.
【变式训练】问题9、方程2-6=7+4的解是(
)
A.=2
B.=-2
C.=1
D.=-1
【总结反思】[合学]回顾学习过程,完善思维框架
地[引导讲解板书]
构建知识体系[师生合作完成]
知识总结
名称
定义
注意事项
建立一元
一次方程
叫做建立方程
单位要统一
方程
一元一
次方程
方程的解
检验时,应将未知数的值代入
方法规律
1.根据实际问题构建一元一次方程的关键是找出等量关系,其本质是
表示同一对象
2.判断方程是不是一元一次方程时,应抓住
3.检验未知数的值是不是方程解的步骤:代入、计算、比较、判断
三、评价练习
【课堂作业】教材第85页A组第1、2、3。(第1题做在书上)
【课后思考】若=-2是关于的方程2+5=3的解,求的值。
附:板书设计
4
所用教材:湘教版初中数学七年级上册第83页。
教学目标:
1、借助高铁的现实情境,经历“把实际问题抽象为方程”的过程,体会方程是刻画现实世界数量关系的有效模型,培养观察、归纳、抽象、概括等能力。感受数学与生活的联系,增强学习数学的信心和民族自豪感。
2、经历方程、一元一次方程概念形成过程,体验从特殊到一般、分类思想。能识别方程、一元一次方程。会检验一个数是不是方程的解。
重点:一元一次方程概念的形成。
难点:建立方程模型,检验一个数是不是方程的解。
教学方法:问题导学、动手实践、交流讨论。
教学过程:一、情境导入
[提问]同学们坐过高速列车吗?你知道高速列车的平均速度大约是多少?
问题1、(1)甲、乙两站之间的高速铁路长1068,“和谐号”高速列车的平均速度为300/,则高速列车从甲站开往乙站需要多少时间?(用两种不同的方法求解)
(2)在小学已学过简易方程,请写出不同形式的2个简易方程:
、
。
[学生独立完成,各组代表在班上交流,教师用多媒体演示]`
二、引导探究
1、方程的概念
【构建模型】[独学]独立思考,用列方程的方法求解教材第83页“动脑筋”题。
问题1、(1)教材第83页动脑筋第(1)题。(2)教材第83页动脑筋第(2)题。
[学法指导](1)阅读题目,①熟悉背景,明确问题。这是什么问题?这个问题中基本量之间的关系是什么?
②进行标记,在题中划出关键的字、词、句。
(2)运用图表,建立关系。如“线段图、表格式”,抓入“列方程的本质是,从两个角度(也就是用两种方式)表示同一对象”(即等量关系)。
[引导]第(1)题:这是行程问题,其基本量(路程、速度、时间)的关系是什么?
用“线段图”进行分析。设
。
百度
[提供学习支持]
列方程:
。
(质疑)教材中“线段图”上标出的量存在问题。
[引导]第(2)题:①长方体形表面是由哪些面
构成的?各个面之间又有何关系?②它的每个面是
长方形,其基本量是长方形的面积应如何表示?
百度
[提供学习支持]
设包装盒的底面宽是y
各个面的名称
上底面
下底面
前侧面
后侧面
左侧面
右侧面
每个面的面积
长方体
的表面积
方式一
方式二
列方程:
。
[自学]阅读教材第83页倒数第3行至第84页第4行内容。
[导学]问题2、
(1)标出方程定义中关键词,方程概念应抓住的要点是:
。
(2)前面所列出的3个方程:300=1068,2.5+318=1068,2.4+2+2.4=6.8中,
所含的未知数分别是
、
、
。
从未知数的角度出发,你再举几个与上述方程形式不同的方程:
,它们所含未知数分别是:
。
(教师巡视指导,捕捉亮点与问题)
[交流]各组代表展示,教师有多媒体演示。
[讲解]反思“建立方程”过程,构建思维框架:[教师边讲边板书]
【变式训练】
问题3、(1)下列各式中,属于方程的是(
)
A.
B.
>1
C.
25+3=28
D.
2+1=3
(2)教材第85页第4行第3题
2、一元一次方程的定义
在前面学习中,我们得到了很多方程,把这些形形色色的方程放在一起,请各组合作学习,完成问题4。
问题4、观察下列方程,将它们按照自己设定的标准进行分类。
①300=1068,②
2.5+318=1068,③2.4+2+2.4=6.8,④,
⑤25=3.14,⑥+5=8,⑦,⑧.
[合学]各小组展开讨论,探究可能的分类方法,由代表在班上展示交流。
[点拨]可以围绕“未知数”分析。
[交流]可能的分类方法如下:
(1)按照未知数的个数进行分类:含一个未知数的有
,含有两个未知数的有
。
(2)按照未知数的次数进行分类:未知数次数为1次的有
,未知数次数为2的有
。
(3)既按照未知数的个数,又按照未知数的次数进行分类:未知数个数为1,并且未知数的次数是1的有
,其余的为一组。
我们把第(3)种分类方法得到的第一组方程叫一元一次方程。请同学们用自己的话说一说什么是“一元一次方程”。
[自学]阅读教材第84页的“一元一次方程的定义”,标出关键字、词。你再举几个一元一次方程的例子:
。
[讨论](1)你能说说“元”和“次”的具体含义。
(2)有学生说“2.4+2+2.4=6.8”不是一元一次方程?对吗?
【变式训练】问题5、
(1)下列方程中是一元一次方程的是(
)。
A.
B.
C.
D.
(2)若关于的方程2-3=1是一元一次方程,则=
。
3、方程的解
[练习]问题6、同学们在小学已学习了简易方程的解法,请求出下列方程中未知数的值
(1)+5=8,
(2)300=1068.
[讲解]方程的解的定义及说明。
(反思)对第84页“方程的解”,你是如何理解的?能举例子说明吗?
(提出问题)哪么如何检验未知数的值是不是方程的解呢?
[讨论]问题7、小明、小红同学分别求出问题6(1)、(2)的未知数的值分别是=3和=3.6后,为了判断结果是不是正确的,写出检验如下,请你判断其检验过程是否正确?
[质疑]阅读教材第84页,你认为这个验证过程是否存在问题?
【尝试练习】问题8、检验=2是不是方程2-6=7+4的解。[先独做,再由一名学生上台板书]
[讨论]检验未知数的值是不是方程的解有几个步骤?代入时应注意什么?
(归纳)检验方程的解的步骤
①代入:将未知数的值分别代入方程的左边和右边;
②计算:分别计算方程左边和右边的值;
③比较:比较左边和右边是不相等;
④判断:若相等,则是;若不相等,则不是.
【变式训练】问题9、方程2-6=7+4的解是(
)
A.=2
B.=-2
C.=1
D.=-1
【总结反思】[合学]回顾学习过程,完善思维框架
地[引导讲解板书]
构建知识体系[师生合作完成]
知识总结
名称
定义
注意事项
建立一元
一次方程
叫做建立方程
单位要统一
方程
一元一
次方程
方程的解
检验时,应将未知数的值代入
方法规律
1.根据实际问题构建一元一次方程的关键是找出等量关系,其本质是
表示同一对象
2.判断方程是不是一元一次方程时,应抓住
3.检验未知数的值是不是方程解的步骤:代入、计算、比较、判断
三、评价练习
【课堂作业】教材第85页A组第1、2、3。(第1题做在书上)
【课后思考】若=-2是关于的方程2+5=3的解,求的值。
附:板书设计
4
同课章节目录
