北师大版九年级数学下册 1.1 锐角三角函数 同步测试题(Word版有答案)
文档属性
| 名称 | 北师大版九年级数学下册 1.1 锐角三角函数 同步测试题(Word版有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 86.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 00:00:00 | ||
图片预览


文档简介
10490200106934001231900001.1 锐角三角函数 同步测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 在Rt△ABC中,∠A=90?,AC=5,BC=13,那么tanB的值是( )
A.512 B.125 C.1213 D.513
?
2. 当角度在0?到90?之间变化时,函数值随着角度的增大而增大的三角函数是( )
A.正弦和余弦 B.正弦和正切
C.余弦和正切 D.正弦、余弦和正切
?3. 已知α是锐角,且sinα=0.75,则( )
A.0?<α<30? B.30?<α<45? C.45?<α<60? D.60?<α<90?
?
4. 在△ABC中,∠ACB=90?,CD⊥AB交于点D,则下列等式中错误的是( )
A.sinB=ACAB B.sinB=ADAC C.sinB=BDBC D.sinB=CDBC
?
5. 在Rt△ABC中,∠C=90?,则BCAB表示( )
A.sinA B.cosA C.sinB D.以上都不对
?
6. 在Rt△ABC中,∠C=90?,AB=13,BC=12,则下列关系式中正确的是( )
A.sinA>cosB B.cosA>sinB C.cosA?
7. 已知Rt△ABC中,∠C=90?,AB=13,BC=5,则sinB的值是( )
A.315 B.1213 C.512 D.135
?
8. α是锐角,且cosα=34,则( )
A.0?<α<30? B.30?<α<45? C.45?<α<60? D.60?<α<90?
?
9. 在Rt△ABC中,∠C=90?,a,b,c分别是∠A,∠B,∠C的对边,下列关系式中错误的是( )
A.b=c?cosB B.b=a?tanB C.a=c?sinA D.a=b?cotB
?
10. 当∠A为锐角,且cosA的值大于12时,则∠A( )
A.大于30? B.小于30? C.大于60? D.小于60?
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 比较大小:sin47?56'________cos47?56'(选填“<”,“>”或“=”).
?
12. 在△ABC中,∠ACB=90?,CD⊥AB,AC=3,BC=4,则tan∠ACD=________.
?
13. 在△ABC中,∠C=90?,BC=6,sinA=23,则AB边的长是________.
?
14. 在△ABC中,∠C=90?,a,b,c分别是∠A,∠B,∠C的对边,若c=3a,则sinA=________.
?
15. 在Rt△ABC中,∠C=90?,若AC=2BC,则tanA的值是________.
?
16. 已知tanα=23,则锐角α的取值范围是________.
?
17. 在Rt△ABC中,∠C=90?,AC=2,BC=3,则cosA=________.
?18. 已知α为锐角,若cosα=0.4321,则锐角α的范围在特殊锐角________之间.
?
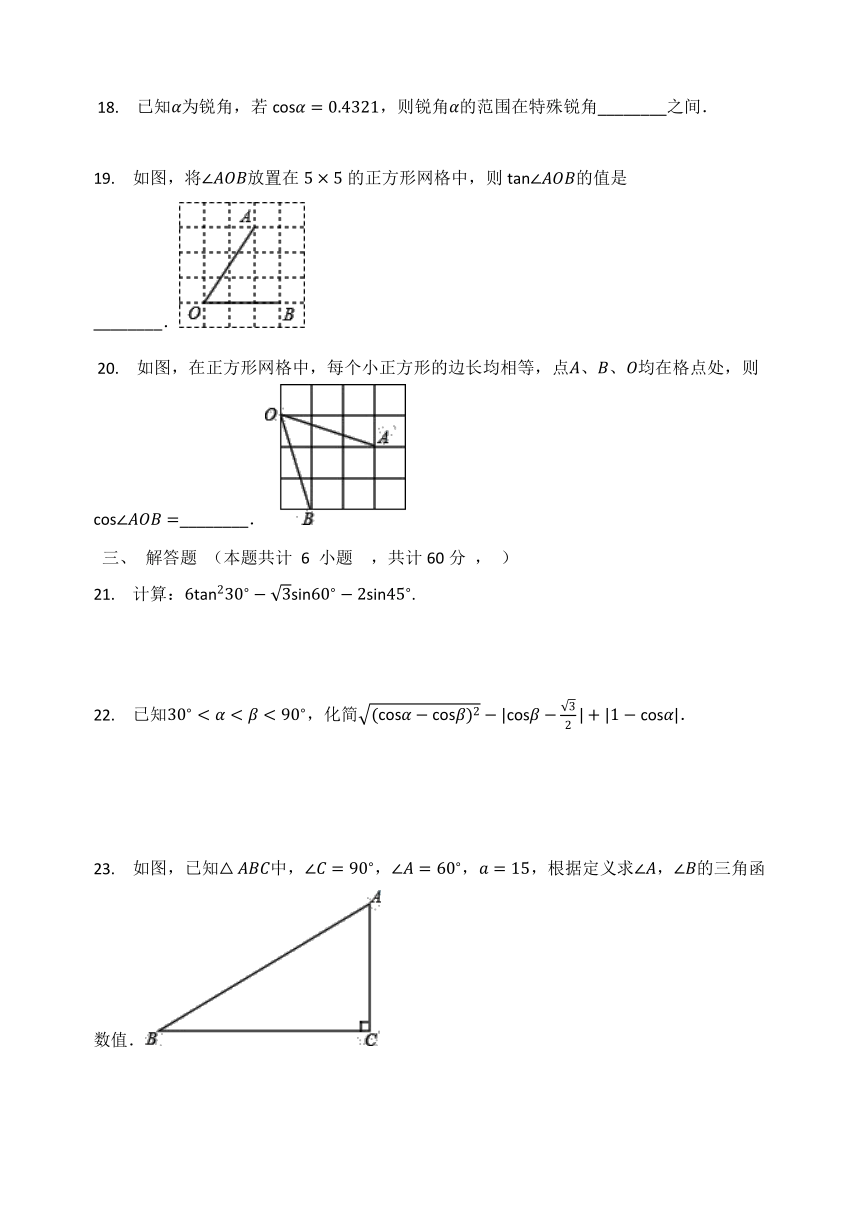
19. 如图,将∠AOB放置在5×5的正方形网格中,则tan∠AOB的值是________.
?20. 如图,在正方形网格中,每个小正方形的边长均相等,点A、B、O均在格点处,则cos∠AOB=________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 计算:6tan230?-3sin60?-2sin45?.
?
22. 已知30?<α<β<90?,化简(cosα-cosβ)2-|cosβ-32|+|1-cosα|.
?
23. 如图,已知△ABC中,∠C=90?,∠A=60?,a=15,根据定义求∠A,∠B的三角函数值.
?
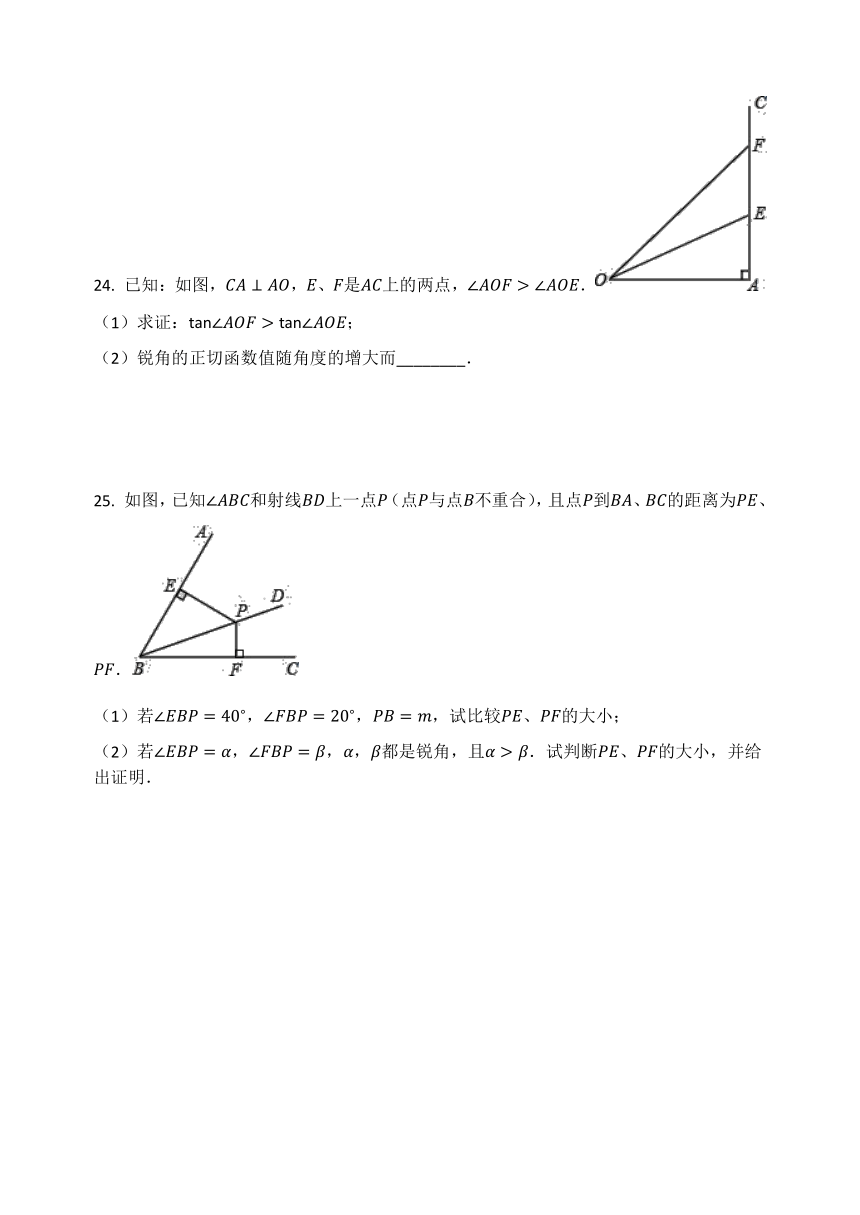
24. 已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.
(1)求证:tan∠AOF>tan∠AOE;
(2)锐角的正切函数值随角度的增大而________.
?
25. 如图,已知∠ABC和射线BD上一点P(点P与点B不重合),且点P到BA、BC的距离为PE、PF.
(1)若∠EBP=40?,∠FBP=20?,PB=m,试比较PE、PF的大小;
(2)若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β.试判断PE、PF的大小,并给出证明.
?
26.
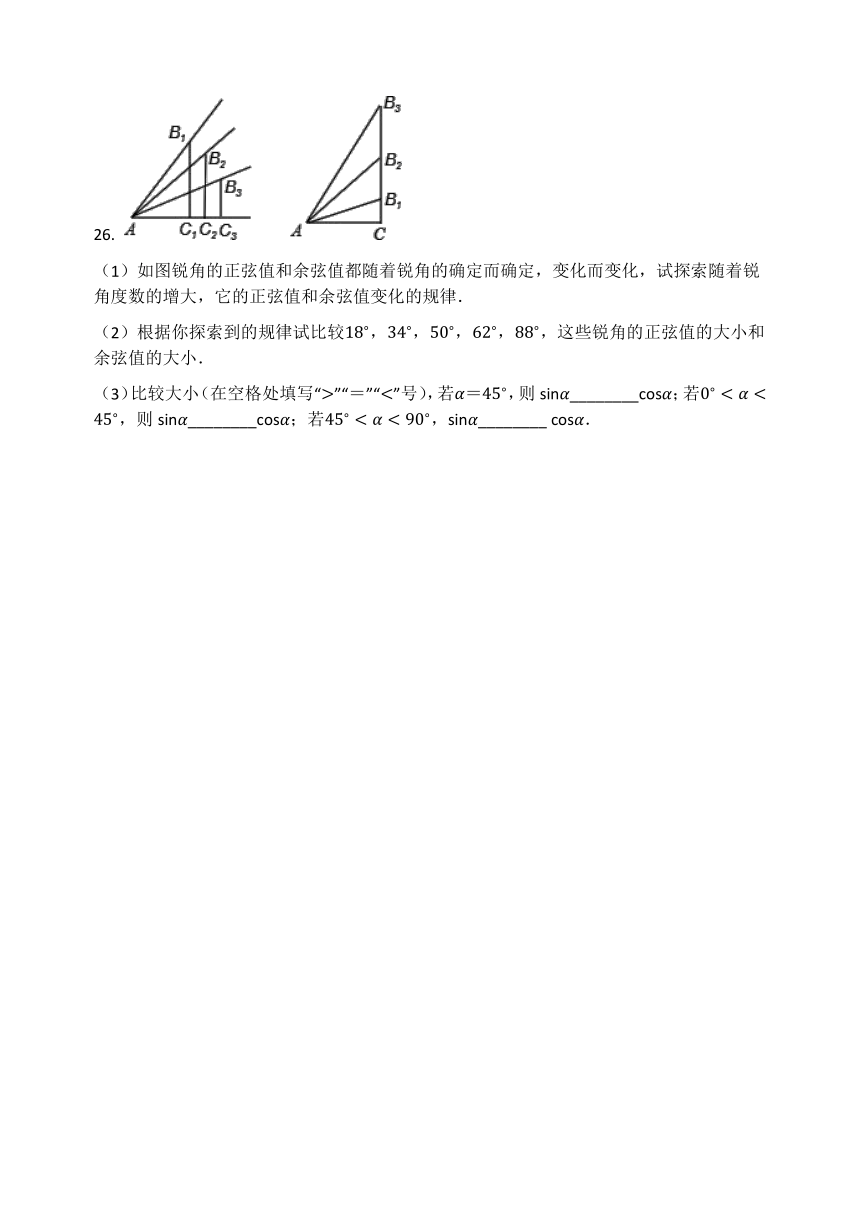
(1)如图锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律试比较18?,34?,50?,62?,88?,这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在空格处填写“>”“=”“<”号),若α=45?,则sinα________cosα;若0?<α<45?,则sinα________cosα;若45?<α<90?,sinα________?cosα.
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
A
【解答】
∵ 在Rt△ABC中,∠A=90?,AC=5,BC=13,
∴ AB=BC2-AC2=12,
∴ tanB=ACAB=512.
2.
【答案】
B
【解答】
解:当角度在0?到90?之间变化时,函数值随着角度的增大而增大的三角函数是正弦和正切.
故选B.
3.
【答案】
C
【解答】
∵ sin60?=32≈0.87,sin45?=22≈0.7,正弦值随角度的增大而增大,
∴ sinα=0.75,则45?<α<60?.
4.
【答案】
C
【解答】
解:A、∵ 在Rt△ACB中,∠ACB=90?,
∴ sinB=ACAB,故本选项错误;
B、∵ CD⊥AB,
∴ ∠ADC=∠ACB=90?,
∴ ∠B+∠A=90?,∠A+∠ACD=90?,
∴ ∠B=∠ACD,
∵ 在Rt△ADC中,∠ADC=90?,sin∠ACD=ADAC,
∴ sinB=ADAC,故本选项错误;
C、∵ ∠B≠∠BCD,sin∠BCD=BDBC,
∴ sinB≠BDBC,故本选项正确;
D、在Rt△BDC中,sinB=CDBC,故本选项错误;
故选C.
5.
【答案】
A
【解答】
解:∵ Rt△ABC中,∠C=90?,
则BCAB表示sinA.
故选A.
6.
【答案】
C
【解答】
解:根据勾股定理,得
AC=5.
再根据锐角三角函数的定义,得
sinA=cosB=1213,cosA=sinB=513.
显然C正确.
故选C.
7.
【答案】
B
【解答】
解:AC=AB2-BC2=132-52=12,
则sinB=ACAB=1213.
故选B.
8.
【答案】
B
【解答】
解:∵ 在锐角三角函数中,余切值都是随着角的增大而减小,
又知cos30?=32,cos45?=22,
故30?<α<45?,
故选B.
9.
【答案】
A
【解答】
解:在Rt△ABC中,∠C=90?,
则cosA=bc,sinA=ac,
tanB=ba,cosB=ac,
tanA=ab,cotA=ba;
因而b=ccosA=atanB,
a=csinA=ccosB=btanA=bcotA,
错误的是b=c?cosB.
故选A.
10.
【答案】
D
【解答】
解:∵ cos60?=12,余弦函数随角增大而减小,
∴ ∠A<60?.
故选D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
>
【解答】
解:∵ cos47?56'=sin(90?-47?56')=sin43?4',
sin47?56'>sin43?4',
∴ sin47?56'>cos47?56'.
故答案为:>.
12.
【答案】
34
【解答】
解:∵ ∠C=90?,CD⊥AB,
∴ ∠B+∠BCD=90?,∠BCD+∠ACD=90?,
∴ ∠ACD=∠B,
∴ tan∠ACD=tan∠B=ACBC=34,
故答案为:34.
13.
【答案】
9
【解答】
解:∵ BC=6,sinA=23,
∴ 23=6AB,
解得:AB=9.
故答案为:9.
14.
【答案】
13
【解答】
解:sinA=ac=a3a=13,
故答案为:13.
15.
【答案】
12
【解答】
解:∵ 在Rt△ABC中,∠C=90?,AC=2BC,
∴ tanA=BCAC=BC2BC=12,
故答案为:12.
16.
【答案】
30?<α<45?
【解答】
解:∵ tan30?=33,tan45?=1,正切函数随角增大而增大,
33∴ 30?<α<45?.
17.
【答案】
21313
【解答】
解:在Rt△ABC中,∠C=90?,AC=2,BC=3,
由勾股定理可得AB=13.
则cosA=ACAB=213=21313.
18.
【答案】
60?【解答】
解:∵ cos30?=32,cos45?=22,cos60?=12,且0.4321<12,
∴ cosα∴ 锐角α的范围是:60?故答案是:60?19.
【答案】
32
【解答】
解:由图可得tan∠AOB=32.
故答案为:32.
20.
【答案】
35
【解答】
解:如图,连接AB,过A作AD⊥OB,
设每个小正方形边长为1,
∵ S△AOB=3×3-12×1×3×2-12×2×2=4,
由勾股定理可得:OA=OB=10,
∴ AD=810=4510,
∴ OD=3510,
∴ cos∠AOB=ODOA=35,
cos∠AOB=35,
故答案为35.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:原式=6×(33)2-3×32-2×22=6×13-32-2=2-32-2=12-2
【解答】
解:原式=6×(33)2-3×32-2×22=6×13-32-2=2-32-2=12-2
22.
【答案】
解:∵ 30?<α<β<90?,
∴ cosα>cosβ,cosβ<32,1-cosα>0,
则原式=cosα-cosβ+cosβ-32+1-cosα=1-32.
【解答】
解:∵ 30?<α<β<90?,
∴ cosα>cosβ,cosβ<32,1-cosα>0,
则原式=cosα-cosβ+cosβ-32+1-cosα=1-32.
23.
【答案】
解:∵ △ABC中,∠C=90?,∠A=60?,a=15,
∴ ∠B=30?,tanA=BCAC=3,
解得:AC=53,则AB=103,
∴ sinA=15103=32,cosA=53103=12,tanA=1553=3,
sinB=12,cosB=32,tanB=33.
【解答】
解:∵ △ABC中,∠C=90?,∠A=60?,a=15,
∴ ∠B=30?,tanA=BCAC=3,
解得:AC=53,则AB=103,
∴ sinA=15103=32,cosA=53103=12,tanA=1553=3,
sinB=12,cosB=32,tanB=33.
24.
【答案】
增大.
【解答】
解:(1)∵ CA⊥AO,
∴ △FOA和△EOA均为直角三角形.
∴ tan∠AOF=AFOA,tan∠AOE=EAOA.
∴ tan∠AOF>tan∠AOE.
(2)由(1)可知锐角的正切函数值随角度的增大而增大.
25.
【答案】
解:(1)在Rt△BPE中,sin∠EBP=PEBP=sin40?
在Rt△BPF中,sin∠FBP=PFBP=sin20?
又sin40?>sin20?
∴ PE>PF;
(2)根据(1)得
sin∠EBP=PEBP=sinα,sin∠FBP=PFBP=sinβ
又∵ α>β
∴ sinα>sinβ
∴ PE>PF.
【解答】
解:(1)在Rt△BPE中,sin∠EBP=PEBP=sin40?
在Rt△BPF中,sin∠FBP=PFBP=sin20?
又sin40?>sin20?
∴ PE>PF;
(2)根据(1)得
sin∠EBP=PEBP=sinα,sin∠FBP=PFBP=sinβ
又∵ α>β
∴ sinα>sinβ
∴ PE>PF.
26.
【答案】
在图中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵ sin∠B1AC=B1C1AB1,sin∠B2AC=B2C2AB2,sin∠B3AC=B3C3AB3,
而B1C1AB1>B2C2AB2>B3C3AB3,
∴ sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图中,Rt△ACB3中,∠C=90?,
cos∠B1AC=ACAB1,cos∠B2AC=ACAB2,cos∠B3AC=ACAB3,
∵ AB3>AB2>AB1,
∴ ACAB1>ACAB2>ACAB3.
即cos∠B3AC结论:锐角的正弦值随角度的增大而增大,锐角的余弦值随角度的增大而减小.
由(1)可知:
sin88?>sin62?>sin50?>sin34?>sin18?;
cos88?=,<,>
【解答】
在图中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵ sin∠B1AC=B1C1AB1,sin∠B2AC=B2C2AB2,sin∠B3AC=B3C3AB3,
而B1C1AB1>B2C2AB2>B3C3AB3,
∴ sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图中,Rt△ACB3中,∠C=90?,
cos∠B1AC=ACAB1,cos∠B2AC=ACAB2,cos∠B3AC=ACAB3,
∵ AB3>AB2>AB1,
∴ ACAB1>ACAB2>ACAB3.
即cos∠B3AC结论:锐角的正弦值随角度的增大而增大,锐角的余弦值随角度的增大而减小.
由(1)可知:
sin88?>sin62?>sin50?>sin34?>sin18?;
cos88?若α=45?,则sinα=cosα;若0?<α<45?,则sinαcosα.
故答案为:=,<,>.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 在Rt△ABC中,∠A=90?,AC=5,BC=13,那么tanB的值是( )
A.512 B.125 C.1213 D.513
?
2. 当角度在0?到90?之间变化时,函数值随着角度的增大而增大的三角函数是( )
A.正弦和余弦 B.正弦和正切
C.余弦和正切 D.正弦、余弦和正切
?3. 已知α是锐角,且sinα=0.75,则( )
A.0?<α<30? B.30?<α<45? C.45?<α<60? D.60?<α<90?
?
4. 在△ABC中,∠ACB=90?,CD⊥AB交于点D,则下列等式中错误的是( )
A.sinB=ACAB B.sinB=ADAC C.sinB=BDBC D.sinB=CDBC
?
5. 在Rt△ABC中,∠C=90?,则BCAB表示( )
A.sinA B.cosA C.sinB D.以上都不对
?
6. 在Rt△ABC中,∠C=90?,AB=13,BC=12,则下列关系式中正确的是( )
A.sinA>cosB B.cosA>sinB C.cosA
7. 已知Rt△ABC中,∠C=90?,AB=13,BC=5,则sinB的值是( )
A.315 B.1213 C.512 D.135
?
8. α是锐角,且cosα=34,则( )
A.0?<α<30? B.30?<α<45? C.45?<α<60? D.60?<α<90?
?
9. 在Rt△ABC中,∠C=90?,a,b,c分别是∠A,∠B,∠C的对边,下列关系式中错误的是( )
A.b=c?cosB B.b=a?tanB C.a=c?sinA D.a=b?cotB
?
10. 当∠A为锐角,且cosA的值大于12时,则∠A( )
A.大于30? B.小于30? C.大于60? D.小于60?
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 比较大小:sin47?56'________cos47?56'(选填“<”,“>”或“=”).
?
12. 在△ABC中,∠ACB=90?,CD⊥AB,AC=3,BC=4,则tan∠ACD=________.
?
13. 在△ABC中,∠C=90?,BC=6,sinA=23,则AB边的长是________.
?
14. 在△ABC中,∠C=90?,a,b,c分别是∠A,∠B,∠C的对边,若c=3a,则sinA=________.
?
15. 在Rt△ABC中,∠C=90?,若AC=2BC,则tanA的值是________.
?
16. 已知tanα=23,则锐角α的取值范围是________.
?
17. 在Rt△ABC中,∠C=90?,AC=2,BC=3,则cosA=________.
?18. 已知α为锐角,若cosα=0.4321,则锐角α的范围在特殊锐角________之间.
?
19. 如图,将∠AOB放置在5×5的正方形网格中,则tan∠AOB的值是________.
?20. 如图,在正方形网格中,每个小正方形的边长均相等,点A、B、O均在格点处,则cos∠AOB=________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 计算:6tan230?-3sin60?-2sin45?.
?
22. 已知30?<α<β<90?,化简(cosα-cosβ)2-|cosβ-32|+|1-cosα|.
?
23. 如图,已知△ABC中,∠C=90?,∠A=60?,a=15,根据定义求∠A,∠B的三角函数值.
?
24. 已知:如图,CA⊥AO,E、F是AC上的两点,∠AOF>∠AOE.
(1)求证:tan∠AOF>tan∠AOE;
(2)锐角的正切函数值随角度的增大而________.
?
25. 如图,已知∠ABC和射线BD上一点P(点P与点B不重合),且点P到BA、BC的距离为PE、PF.
(1)若∠EBP=40?,∠FBP=20?,PB=m,试比较PE、PF的大小;
(2)若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β.试判断PE、PF的大小,并给出证明.
?
26.
(1)如图锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律试比较18?,34?,50?,62?,88?,这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在空格处填写“>”“=”“<”号),若α=45?,则sinα________cosα;若0?<α<45?,则sinα________cosα;若45?<α<90?,sinα________?cosα.
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
A
【解答】
∵ 在Rt△ABC中,∠A=90?,AC=5,BC=13,
∴ AB=BC2-AC2=12,
∴ tanB=ACAB=512.
2.
【答案】
B
【解答】
解:当角度在0?到90?之间变化时,函数值随着角度的增大而增大的三角函数是正弦和正切.
故选B.
3.
【答案】
C
【解答】
∵ sin60?=32≈0.87,sin45?=22≈0.7,正弦值随角度的增大而增大,
∴ sinα=0.75,则45?<α<60?.
4.
【答案】
C
【解答】
解:A、∵ 在Rt△ACB中,∠ACB=90?,
∴ sinB=ACAB,故本选项错误;
B、∵ CD⊥AB,
∴ ∠ADC=∠ACB=90?,
∴ ∠B+∠A=90?,∠A+∠ACD=90?,
∴ ∠B=∠ACD,
∵ 在Rt△ADC中,∠ADC=90?,sin∠ACD=ADAC,
∴ sinB=ADAC,故本选项错误;
C、∵ ∠B≠∠BCD,sin∠BCD=BDBC,
∴ sinB≠BDBC,故本选项正确;
D、在Rt△BDC中,sinB=CDBC,故本选项错误;
故选C.
5.
【答案】
A
【解答】
解:∵ Rt△ABC中,∠C=90?,
则BCAB表示sinA.
故选A.
6.
【答案】
C
【解答】
解:根据勾股定理,得
AC=5.
再根据锐角三角函数的定义,得
sinA=cosB=1213,cosA=sinB=513.
显然C正确.
故选C.
7.
【答案】
B
【解答】
解:AC=AB2-BC2=132-52=12,
则sinB=ACAB=1213.
故选B.
8.
【答案】
B
【解答】
解:∵ 在锐角三角函数中,余切值都是随着角的增大而减小,
又知cos30?=32,cos45?=22,
故30?<α<45?,
故选B.
9.
【答案】
A
【解答】
解:在Rt△ABC中,∠C=90?,
则cosA=bc,sinA=ac,
tanB=ba,cosB=ac,
tanA=ab,cotA=ba;
因而b=ccosA=atanB,
a=csinA=ccosB=btanA=bcotA,
错误的是b=c?cosB.
故选A.
10.
【答案】
D
【解答】
解:∵ cos60?=12,余弦函数随角增大而减小,
∴ ∠A<60?.
故选D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
>
【解答】
解:∵ cos47?56'=sin(90?-47?56')=sin43?4',
sin47?56'>sin43?4',
∴ sin47?56'>cos47?56'.
故答案为:>.
12.
【答案】
34
【解答】
解:∵ ∠C=90?,CD⊥AB,
∴ ∠B+∠BCD=90?,∠BCD+∠ACD=90?,
∴ ∠ACD=∠B,
∴ tan∠ACD=tan∠B=ACBC=34,
故答案为:34.
13.
【答案】
9
【解答】
解:∵ BC=6,sinA=23,
∴ 23=6AB,
解得:AB=9.
故答案为:9.
14.
【答案】
13
【解答】
解:sinA=ac=a3a=13,
故答案为:13.
15.
【答案】
12
【解答】
解:∵ 在Rt△ABC中,∠C=90?,AC=2BC,
∴ tanA=BCAC=BC2BC=12,
故答案为:12.
16.
【答案】
30?<α<45?
【解答】
解:∵ tan30?=33,tan45?=1,正切函数随角增大而增大,
33
17.
【答案】
21313
【解答】
解:在Rt△ABC中,∠C=90?,AC=2,BC=3,
由勾股定理可得AB=13.
则cosA=ACAB=213=21313.
18.
【答案】
60?
解:∵ cos30?=32,cos45?=22,cos60?=12,且0.4321<12,
∴ cosα
【答案】
32
【解答】
解:由图可得tan∠AOB=32.
故答案为:32.
20.
【答案】
35
【解答】
解:如图,连接AB,过A作AD⊥OB,
设每个小正方形边长为1,
∵ S△AOB=3×3-12×1×3×2-12×2×2=4,
由勾股定理可得:OA=OB=10,
∴ AD=810=4510,
∴ OD=3510,
∴ cos∠AOB=ODOA=35,
cos∠AOB=35,
故答案为35.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:原式=6×(33)2-3×32-2×22=6×13-32-2=2-32-2=12-2
【解答】
解:原式=6×(33)2-3×32-2×22=6×13-32-2=2-32-2=12-2
22.
【答案】
解:∵ 30?<α<β<90?,
∴ cosα>cosβ,cosβ<32,1-cosα>0,
则原式=cosα-cosβ+cosβ-32+1-cosα=1-32.
【解答】
解:∵ 30?<α<β<90?,
∴ cosα>cosβ,cosβ<32,1-cosα>0,
则原式=cosα-cosβ+cosβ-32+1-cosα=1-32.
23.
【答案】
解:∵ △ABC中,∠C=90?,∠A=60?,a=15,
∴ ∠B=30?,tanA=BCAC=3,
解得:AC=53,则AB=103,
∴ sinA=15103=32,cosA=53103=12,tanA=1553=3,
sinB=12,cosB=32,tanB=33.
【解答】
解:∵ △ABC中,∠C=90?,∠A=60?,a=15,
∴ ∠B=30?,tanA=BCAC=3,
解得:AC=53,则AB=103,
∴ sinA=15103=32,cosA=53103=12,tanA=1553=3,
sinB=12,cosB=32,tanB=33.
24.
【答案】
增大.
【解答】
解:(1)∵ CA⊥AO,
∴ △FOA和△EOA均为直角三角形.
∴ tan∠AOF=AFOA,tan∠AOE=EAOA.
∴ tan∠AOF>tan∠AOE.
(2)由(1)可知锐角的正切函数值随角度的增大而增大.
25.
【答案】
解:(1)在Rt△BPE中,sin∠EBP=PEBP=sin40?
在Rt△BPF中,sin∠FBP=PFBP=sin20?
又sin40?>sin20?
∴ PE>PF;
(2)根据(1)得
sin∠EBP=PEBP=sinα,sin∠FBP=PFBP=sinβ
又∵ α>β
∴ sinα>sinβ
∴ PE>PF.
【解答】
解:(1)在Rt△BPE中,sin∠EBP=PEBP=sin40?
在Rt△BPF中,sin∠FBP=PFBP=sin20?
又sin40?>sin20?
∴ PE>PF;
(2)根据(1)得
sin∠EBP=PEBP=sinα,sin∠FBP=PFBP=sinβ
又∵ α>β
∴ sinα>sinβ
∴ PE>PF.
26.
【答案】
在图中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵ sin∠B1AC=B1C1AB1,sin∠B2AC=B2C2AB2,sin∠B3AC=B3C3AB3,
而B1C1AB1>B2C2AB2>B3C3AB3,
∴ sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图中,Rt△ACB3中,∠C=90?,
cos∠B1AC=ACAB1,cos∠B2AC=ACAB2,cos∠B3AC=ACAB3,
∵ AB3>AB2>AB1,
∴ ACAB1>ACAB2>ACAB3.
即cos∠B3AC
由(1)可知:
sin88?>sin62?>sin50?>sin34?>sin18?;
cos88?
【解答】
在图中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵ sin∠B1AC=B1C1AB1,sin∠B2AC=B2C2AB2,sin∠B3AC=B3C3AB3,
而B1C1AB1>B2C2AB2>B3C3AB3,
∴ sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图中,Rt△ACB3中,∠C=90?,
cos∠B1AC=ACAB1,cos∠B2AC=ACAB2,cos∠B3AC=ACAB3,
∵ AB3>AB2>AB1,
∴ ACAB1>ACAB2>ACAB3.
即cos∠B3AC
由(1)可知:
sin88?>sin62?>sin50?>sin34?>sin18?;
cos88?
故答案为:=,<,>.
