华东师大版数学八年级上册导学案:14.1勾股定理(1)(表格式 无答案)
文档属性
| 名称 | 华东师大版数学八年级上册导学案:14.1勾股定理(1)(表格式 无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 87.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 21:58:56 | ||
图片预览

文档简介
课题:勾股定理(1)
授课教师:
学科组长:
教研组长:
学习目标:
1、让学生通过观察、计算、猜想直角三角形两条直角边的平方和等于斜边的平方的结论。
2、掌握勾股定理的内容,会用面积法证明勾股定理。
学习重点:
探索直角三角形两条直角边的平方和等于斜边的平方的结论,从而发展勾股定理.
学习难点:
以直角三角形的边为边的正方形面积的计算.
学习过程:
一、课前预习
1、阅读课本第64页至第65页。
2、习题:
二、自主学习
你能发现下图中等腰直角三角形ABC有什么性质吗?
问题1:等腰直角三角形都有上述性质吗?
观察下图,并回答问题:
三、合作探究
问题2:等腰三角形有上述性质,其他的三角形也有这个性质吗?如下图,每个小方格的面积均为1,请分别计算出下图中正方形A、B、C,A′、B′、C′的面积,看看能得出什么结论.(提示:以斜边为边长的正方形的面积,等于虚线标出的正方形的面积减去四个直角三角形的面积.)
到现在你知道a、b、c作为直角三角形的三边(其中c为斜边),有怎样的关系?
从我们实验的大量数据中,你对直角三角形三边的数量关系有什么猜想?
勾股定理:
小测试:在△ABC中,∠C=90°。
(1)若a=8,b=6,则c=_____.
(2)若a=16,b=12,则c=_____.
(3)若b=12,c=13,则a=_____.
四、分层训练
★1、如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
(1)两锐角之间的关系:
;
(2)若∠B=30°,则∠B的对边和斜边:
;
(3)三边之间的关系:
。
★2、一个直角三角形中,两直角边长分别为3和4,下列说法正确的是(
)
A.斜边长为25
B.三角形周长为25
C.斜边长为5
D.三角形面积为20
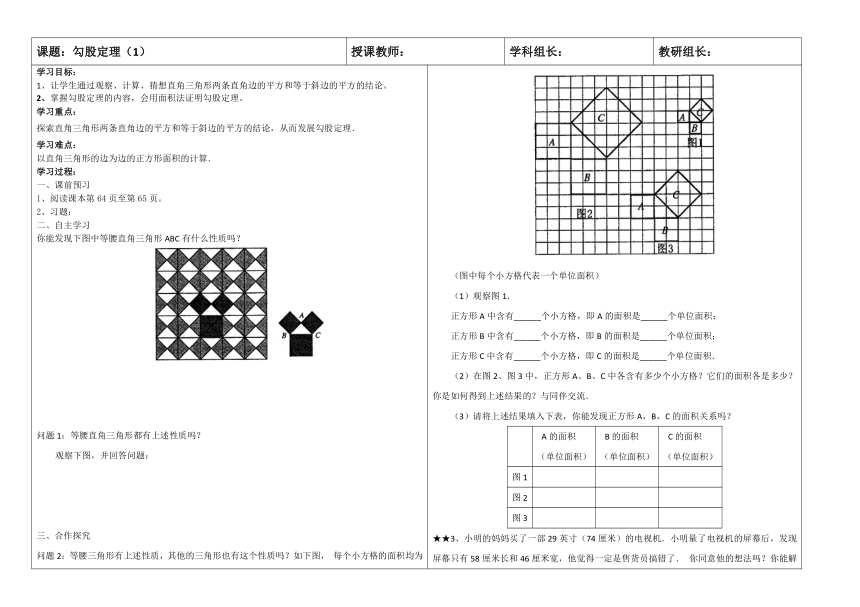
(图中每个小方格代表一个单位面积)
(1)观察图1.
正方形A中含有______个小方格,即A的面积是______个单位面积;
正方形B中含有______个小方格,即B的面积是______个单位面积;
正方形C中含有______个小方格,即C的面积是______个单位面积.
(2)在图2、图3中,正方形A、B、C中各含有多少个小方格?它们的面积各是多少?你是如何得到上述结果的?与同伴交流.
(3)请将上述结果填入下表,你能发现正方形A,B,C的面积关系吗?
A的面积
(单位面积)
B的面积
(单位面积)
C的面积
(单位面积)图1图2图3
★★3、小明的妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你同意他的想法吗?你能解释这是为什么吗?
★★4、如右图,一根旗杆在离地面9m处断裂,旗杆顶部落在离旗杆底部12m处,旗杆折断之前有多高?
★★5、如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为________.
★★★6、利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为弦图.观察图形,验证:c2=a2+b2.
授课教师:
学科组长:
教研组长:
学习目标:
1、让学生通过观察、计算、猜想直角三角形两条直角边的平方和等于斜边的平方的结论。
2、掌握勾股定理的内容,会用面积法证明勾股定理。
学习重点:
探索直角三角形两条直角边的平方和等于斜边的平方的结论,从而发展勾股定理.
学习难点:
以直角三角形的边为边的正方形面积的计算.
学习过程:
一、课前预习
1、阅读课本第64页至第65页。
2、习题:
二、自主学习
你能发现下图中等腰直角三角形ABC有什么性质吗?
问题1:等腰直角三角形都有上述性质吗?
观察下图,并回答问题:
三、合作探究
问题2:等腰三角形有上述性质,其他的三角形也有这个性质吗?如下图,每个小方格的面积均为1,请分别计算出下图中正方形A、B、C,A′、B′、C′的面积,看看能得出什么结论.(提示:以斜边为边长的正方形的面积,等于虚线标出的正方形的面积减去四个直角三角形的面积.)
到现在你知道a、b、c作为直角三角形的三边(其中c为斜边),有怎样的关系?
从我们实验的大量数据中,你对直角三角形三边的数量关系有什么猜想?
勾股定理:
小测试:在△ABC中,∠C=90°。
(1)若a=8,b=6,则c=_____.
(2)若a=16,b=12,则c=_____.
(3)若b=12,c=13,则a=_____.
四、分层训练
★1、如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
(1)两锐角之间的关系:
;
(2)若∠B=30°,则∠B的对边和斜边:
;
(3)三边之间的关系:
。
★2、一个直角三角形中,两直角边长分别为3和4,下列说法正确的是(
)
A.斜边长为25
B.三角形周长为25
C.斜边长为5
D.三角形面积为20
(图中每个小方格代表一个单位面积)
(1)观察图1.
正方形A中含有______个小方格,即A的面积是______个单位面积;
正方形B中含有______个小方格,即B的面积是______个单位面积;
正方形C中含有______个小方格,即C的面积是______个单位面积.
(2)在图2、图3中,正方形A、B、C中各含有多少个小方格?它们的面积各是多少?你是如何得到上述结果的?与同伴交流.
(3)请将上述结果填入下表,你能发现正方形A,B,C的面积关系吗?
A的面积
(单位面积)
B的面积
(单位面积)
C的面积
(单位面积)图1图2图3
★★3、小明的妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你同意他的想法吗?你能解释这是为什么吗?
★★4、如右图,一根旗杆在离地面9m处断裂,旗杆顶部落在离旗杆底部12m处,旗杆折断之前有多高?
★★5、如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为________.
★★★6、利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为弦图.观察图形,验证:c2=a2+b2.
