华东师大版数学八年级上册导学案:14.1勾股定理逆定理(1)(表格式 无答案)
文档属性
| 名称 | 华东师大版数学八年级上册导学案:14.1勾股定理逆定理(1)(表格式 无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 53.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 21:01:33 | ||
图片预览

文档简介
课题:勾股定理的逆定理(1)
授课教师:
学科组长:
教研组长:
学习目标:
1.
探究勾股定理的逆定理的证明方法.
2.给出三边能判断是否为直角三角形.
学习重点:
勾股定理的逆定理的证明方法.
学习难点:
勾股定理的逆定理的应用。
学习过程:
一、课前预习
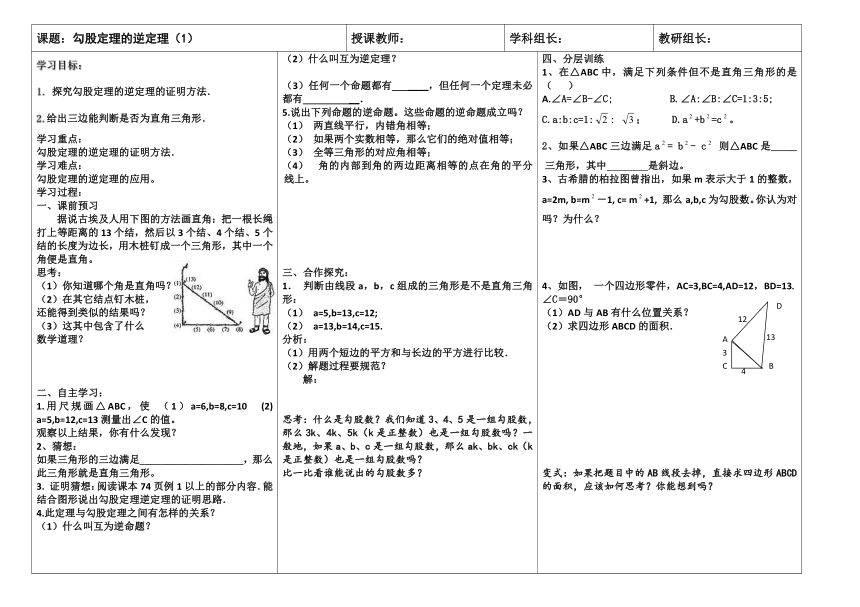
据说古埃及人用下图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结、4个结、5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
思考:
(1)你知道哪个角是直角吗?
(2)在其它结点钉木桩,
还能得到类似的结果吗?
(3)这其中包含了什么
数学道理?
二、自主学习:
1.用尺规画△ABC,使
(1)a=6,b=8,c=10
(2)
a=5,b=12,c=13测量出∠C的值。
观察以上结果,你有什么发现?
2、猜想:
如果三角形的三边满足____________________,那么此三角形就是直角三角形。
3.
证明猜想:阅读课本74页例1以上的部分内容.能结合图形说出勾股定理逆定理的证明思路.
4.此定理与勾股定理之间有怎样的关系?
(1)什么叫互为逆命题?
(2)什么叫互为逆定理?
(3)任何一个命题都有
____,但任何一个定理未必都有
__.
5.说出下列命题的逆命题。这些命题的逆命题成立吗?
两直线平行,内错角相等;
如果两个实数相等,那么它们的绝对值相等;
全等三角形的对应角相等;
角的内部到角的两边距离相等的点在角的平分线上。
三、合作探究:
1.
判断由线段a,b,c组成的三角形是不是直角三角形:
a=5,b=13,c=12;
a=13,b=14,c=15.
分析:
(1)用两个短边的平方和与长边的平方进行比较.
(2)解题过程要规范?
解:
思考:什么是勾股数?我们知道3、4、5是一组勾股数,那么3k、4k、5k(k是正整数)也是一组勾股数吗?一般地,如果a、b、c是一组勾股数,那么ak、bk、ck(k是正整数)也是一组勾股数吗?
比一比看谁能说出的勾股数多?
四、分层训练
1、在△ABC中,满足下列条件但不是直角三角形的是(
)
A.∠A=∠B-∠C;
B.∠A:∠B:∠C=1:3:5;
C.a:b:c=1::
;
D.a+b=c。
2、如果△ABC三边满足a=
b-
c
则△ABC是_____三角形,其中
是斜边。
3、古希腊的柏拉图曾指出,如果m表示大于1的整数,a=2m,
b=m-1,
c=
m+1,
那么a,b,c为勾股数。你认为对吗?为什么?
4、如图,
一个四边形零件,AC=3,BC=4,AD=12,BD=13.∠C=90°
(1)AD与AB有什么位置关系?
(2)求四边形ABCD的面积.
变式:如果把题目中的AB线段去掉,直接求四边形ABCD的面积,应该如何思考?你能想到吗?
课
后
反
思
授课教师:
学科组长:
教研组长:
学习目标:
1.
探究勾股定理的逆定理的证明方法.
2.给出三边能判断是否为直角三角形.
学习重点:
勾股定理的逆定理的证明方法.
学习难点:
勾股定理的逆定理的应用。
学习过程:
一、课前预习
据说古埃及人用下图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结、4个结、5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
思考:
(1)你知道哪个角是直角吗?
(2)在其它结点钉木桩,
还能得到类似的结果吗?
(3)这其中包含了什么
数学道理?
二、自主学习:
1.用尺规画△ABC,使
(1)a=6,b=8,c=10
(2)
a=5,b=12,c=13测量出∠C的值。
观察以上结果,你有什么发现?
2、猜想:
如果三角形的三边满足____________________,那么此三角形就是直角三角形。
3.
证明猜想:阅读课本74页例1以上的部分内容.能结合图形说出勾股定理逆定理的证明思路.
4.此定理与勾股定理之间有怎样的关系?
(1)什么叫互为逆命题?
(2)什么叫互为逆定理?
(3)任何一个命题都有
____,但任何一个定理未必都有
__.
5.说出下列命题的逆命题。这些命题的逆命题成立吗?
两直线平行,内错角相等;
如果两个实数相等,那么它们的绝对值相等;
全等三角形的对应角相等;
角的内部到角的两边距离相等的点在角的平分线上。
三、合作探究:
1.
判断由线段a,b,c组成的三角形是不是直角三角形:
a=5,b=13,c=12;
a=13,b=14,c=15.
分析:
(1)用两个短边的平方和与长边的平方进行比较.
(2)解题过程要规范?
解:
思考:什么是勾股数?我们知道3、4、5是一组勾股数,那么3k、4k、5k(k是正整数)也是一组勾股数吗?一般地,如果a、b、c是一组勾股数,那么ak、bk、ck(k是正整数)也是一组勾股数吗?
比一比看谁能说出的勾股数多?
四、分层训练
1、在△ABC中,满足下列条件但不是直角三角形的是(
)
A.∠A=∠B-∠C;
B.∠A:∠B:∠C=1:3:5;
C.a:b:c=1::
;
D.a+b=c。
2、如果△ABC三边满足a=
b-
c
则△ABC是_____三角形,其中
是斜边。
3、古希腊的柏拉图曾指出,如果m表示大于1的整数,a=2m,
b=m-1,
c=
m+1,
那么a,b,c为勾股数。你认为对吗?为什么?
4、如图,
一个四边形零件,AC=3,BC=4,AD=12,BD=13.∠C=90°
(1)AD与AB有什么位置关系?
(2)求四边形ABCD的面积.
变式:如果把题目中的AB线段去掉,直接求四边形ABCD的面积,应该如何思考?你能想到吗?
课
后
反
思
