2020-2021学年山东省东营市垦利区七年级(上)期中数学试卷(五四学制)(Word版含解析)
文档属性
| 名称 | 2020-2021学年山东省东营市垦利区七年级(上)期中数学试卷(五四学制)(Word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 219.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 00:00:00 | ||
图片预览



文档简介
2020-2021学年山东省东营市垦利区七年级(上)期中数学试卷(五四学制)
一、选择题(本题共10小题,共30分.在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,不选或选出的答案超过一个均记零分.)
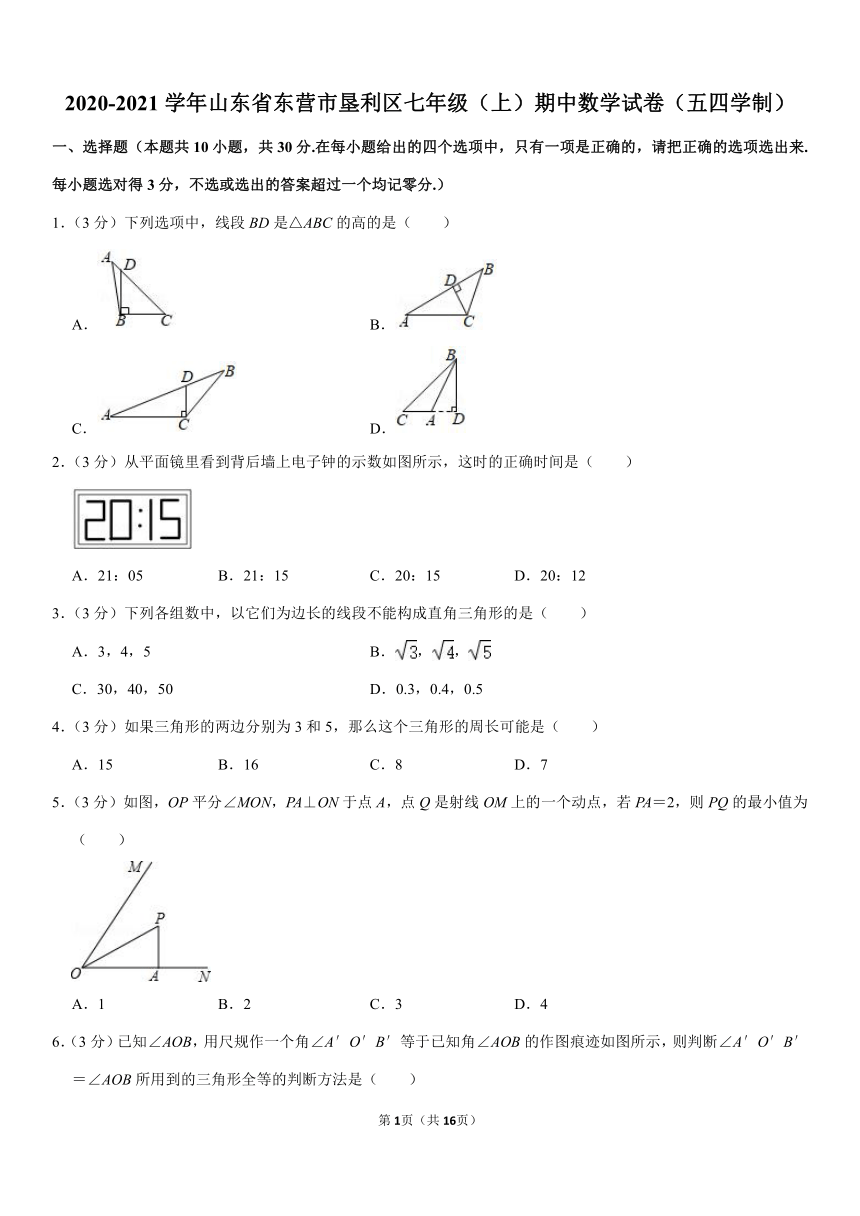
1.(3分)下列选项中,线段BD是△ABC的高的是( )
A.
B.
C.
D.
2.(3分)从平面镜里看到背后墙上电子钟的示数如图所示,这时的正确时间是( )
A.21:05
B.21:15
C.20:15
D.20:12
3.(3分)下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
A.3,4,5
B.,,
C.30,40,50
D.0.3,0.4,0.5
4.(3分)如果三角形的两边分别为3和5,那么这个三角形的周长可能是( )
A.15
B.16
C.8
D.7
5.(3分)如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )
A.1
B.2
C.3
D.4
6.(3分)已知∠AOB,用尺规作一个角∠A′O′B′等于已知角∠AOB的作图痕迹如图所示,则判断∠A′O′B′=∠AOB所用到的三角形全等的判断方法是( )
A.SAS
B.ASA
C.AAS
D.SSS
7.(3分)如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )
A.∠B=∠E
B.∠BAD=∠EAC
C.∠BAC=∠EAD
D.BC=ED
8.(3分)已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A.25
B.7
C.5和7
D.25或7
9.(3分)如图,已知△ABC中,点D、E分别是边BC、AB的中点.若△ABC的面积等于8,则△BDE的面积等于( )
A.2
B.3
C.4
D.5
10.(3分)如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③FG∥AD;④∠AHC=60°;⑤△BFG是等边三角形;其中正确的有( )
A.2个
B.3个
C.4个
D.5个
二、填空题(11-14题,每小题3分,15-18题,每小题3分,共28分)
11.(3分)等腰三角形的两边长分别为4,8,则它的周长为
.
12.(3分)如图,AC=DC,BC=EC,请你添加一个适当的条件:
,使得△ABC≌△DEC.
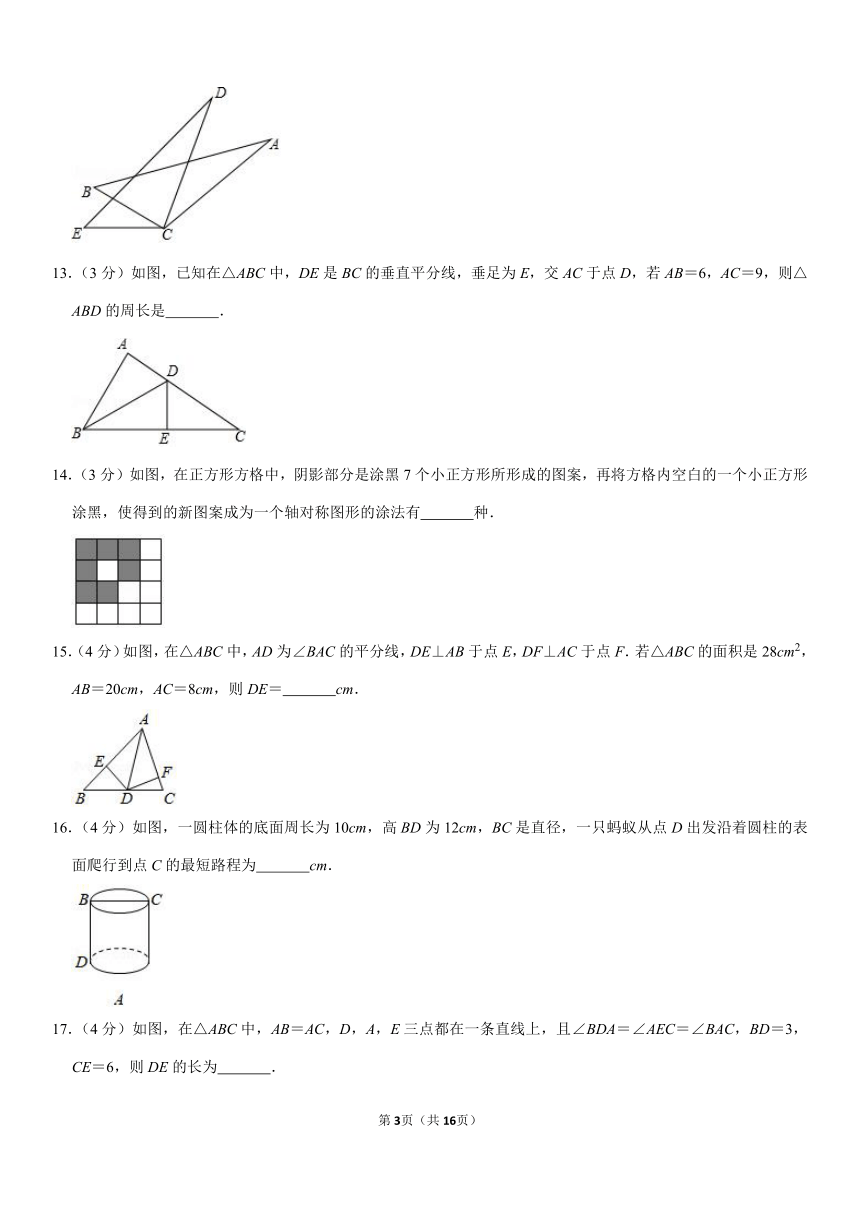
13.(3分)如图,已知在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是
.
14.(3分)如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有
种.
15.(4分)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F.若△ABC的面积是28cm2,AB=20cm,AC=8cm,则DE=
cm.
16.(4分)如图,一圆柱体的底面周长为10cm,高BD为12cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程为
cm.
17.(4分)如图,在△ABC中,AB=AC,D,A,E三点都在一条直线上,且∠BDA=∠AEC=∠BAC,BD=3,CE=6,则DE的长为
.
18.(4分)如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,…,若∠A=70°,则∠An﹣1AnBn﹣1的度数为
.(用含n的代数式表示)
三、解答题(本大题共62分)
19.(6分)如图,已知∠1=∠2,∠B=∠D,求证:CB=CD.
20.(6分)如图,已知:BC∥EF,BC=EF,AE=DB,请判断DF与AC的位置关系,并说明理由.
21.(9分)如图所示的一块地,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m,求这块地的面积.
22.(9分)如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于D;以点A为圆心,AD长为半径画弧,交线段AC于点E,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)设BC=3,AC=4.求AD的长.
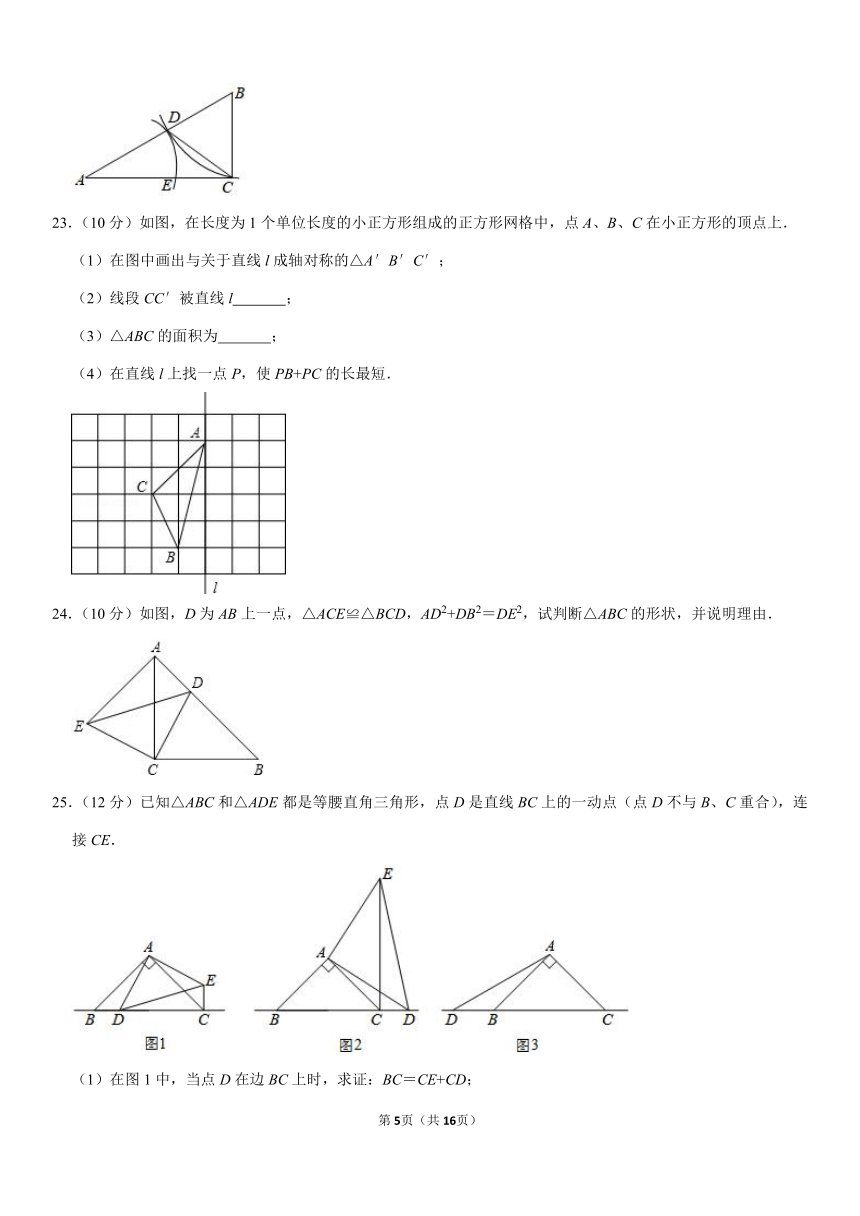
23.(10分)如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与关于直线l成轴对称的△A′B′C′;
(2)线段CC′被直线l
;
(3)△ABC的面积为
;
(4)在直线l上找一点P,使PB+PC的长最短.
24.(10分)如图,D为AB上一点,△ACE≌△BCD,AD2+DB2=DE2,试判断△ABC的形状,并说明理由.
25.(12分)已知△ABC和△ADE都是等腰直角三角形,点D是直线BC上的一动点(点D不与B、C重合),连接CE.
(1)在图1中,当点D在边BC上时,求证:BC=CE+CD;
(2)在图2中,当点D在边BC的延长线上时,结论BC=CE+CD是否还成立?若不成立,请猜想BC、CE、CD之间存在的数量关系,并说明理由;
(3)在图3中,当点D在边BC的反向延长线上时,补全图形,不需写证明过程,直接写出BC、CE、CD之间存在的数量关系.
2020-2021学年山东省东营市垦利区七年级(上)期中数学试卷(五四学制)
试题解析
一、选择题(本题共10小题,共30分.在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,不选或选出的答案超过一个均记零分.)
1.解:线段BD是△ABC的高,则过点B作对边AC的垂线.
故选:D.
2.解:由图分析可得题中所给的“20:15”与“21:05”成轴对称,这时的时间应是21:05.
故选:A.
3.解:A、∵32+32=54,∴能组成直角三角形;
B、∵()2+32≠()4,∴不能组成直角三角形;
C、∵302+402=502,∴能组成直角三角形;
D、∵0.37+0.44=0.57,∴能组成直角三角形.
故选:B.
4.解:设三角形的第三边为x,则2<x<8.故选A.
5.解:
∵垂线段最短,
∴当PQ⊥OM时,PQ有最小值,
又∵OP平分∠MON,PA⊥ON,
∴PQ=PA=2,
故选:B.
6.解:如图,连接CD,
∵在△COD和△C′O′D′中
,
∴△COD≌△C'O'D'(SSS),
∴∠A'O'B'=∠AOB(全等三角形的对应角相等).
故选:D.
7.解:∵AB=AE,AC=AD,
∴当∠BAD=∠EAC或∠BAC=∠EAD,依据SAS即可得到△ABC≌△AED;
当BC=ED时,依据SSS即可得到△ABC≌△AED;
当∠B=∠E时,不能判定△ABC≌△AED.
故选:A.
8.解:分两种情况:
①当3和4为直角边长时,
由勾股定理得:第三边长的平方,即斜边长的平方=62+44=25;
②4为斜边长时,
由勾股定理得:第三边长的平方=46﹣32=2;
综上所述:第三边长的平方是25或7;
故选:D.
9.解:∵点D边BC的中点,△ABC的面积等于8,
∴S△ABD=S△ABC=4,
∵E是AB的中点,
∴S△BDE=S△ABD=2=2,
故选:A.
10.解:∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,
∴∠ABE=∠CBD,
即AB=BC,BD=BE
∴△ABE≌△CBD(SAS),
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60°,
∴△BGD≌△BFE(ASA),
∴BG=BF,∠BFG=∠BGF=60°,
∴∠BGF=∠EBD,
∴FG∥AD;
故①②③正确;
∵△ABE≌△CBD,
∴∠EAB=∠BCD,
∵∠CBA=60°,
∴∠AHC=∠CDB+∠EAB=∠CDB+∠BCD=∠CBA=60°,
故④正确;
∵BF=BG,∠FBG=60°,
∴△BFG是等边三角形,
故⑤正确.
故选:D.
二、填空题(11-14题,每小题3分,15-18题,每小题3分,共28分)
11.解:①当4为腰时,4+6=8;
②当8为腰时,4﹣4<8<3+4.
故此三角形的周长=8+4+4=20.
故答案是:20.
12.解:添加条件是:AB=DE,
在△ABC与△DEC中,,
∴△ABC≌△DEC.
故答案为:AB=DE.本题答案不唯一.
13.解:∵DE是BC的垂直平分线,
∴DB=DC,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=15,
故答案为:15.
14.解:如图,有三种方案,
故答案为3.
15.解:在△ABC中,AD为∠BAC的平分线,DF⊥AC于F,
∴DE=DF,
∴S△ABC=S△ABD+S△ACD=AB?DE+,
∵△ABC面积是28cm2,AB=20cm,AC=3cm,
∴×20DE+,
解得DE=2cm.
故答案为:7.
16.解:如图所示:
由于圆柱体的底面周长为10cm,
则AD=10×=5(cm).
又因为BD=AC=12cm,
所以DC===13(cm).
故蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程为13cm.
故答案为:13.
17.解:∵∠BDA=∠AEC=∠BAC,
∴∠DBA+∠BAD=∠BAD+∠CAE,
∴∠DBA=∠CAE,
∵在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AE+AD=BD+CE=3+6=6.
故答案为:9.
18.解:∵在△ABA1中,∠A=70°1B,
∴∠BA3A=70°,
∵A1A2=A8B1,∠BA1A是△A2A2B1的外角,
∴∠B3A2A1==35°;
同理可得,
∠B2A8A2=17.5°,∠B2A4A3=×17.5°=,
∴∠An﹣1AnBn﹣1=.
故答案为:.
三、解答题(本大题共62分)
19.证明:如图,∵∠1=∠2,
∴∠ACB=∠ACD.
在△ABC与△ADC中,
,
∴△ABC≌△ADC(AAS),
∴CB=CD.
20.解:结论:DF∥AC.
理由:∵AE=BD,
∴DE=AB,
∵EF∥BC,
∴∠E=∠B,
∵EF=BC,
∴△EFD≌△BCA,
∴∠DEF=∠BAC,
∴∠ADF=∠DAC,
∴DF∥AC.
21.解:连接AC.
∵AD=3 m,CD=4 m,
∴AC=m.
∵BC=12 m,AB=13 m,
∴BC2+AC2=125+52=169(m4),AB2=132=169(m3),
∴BC2+AC2=AB2,
∴∠ACB=90°.
∴S四边形ABCD=SRt△ADC+SRt△ABC
=
=
=36(m8).
故这块地的面积为36m2.
22.解:(1)∵∠ACD=90°,∠A=28°,
∴∠B=62°.
∵BD=BC,
∴∠BCD=∠BDC==59°.
∴∠ACD=90°﹣∠BCD=90°﹣59°=31°;
(2)∵∠ACB=90°,BC=3,
由勾股定理得:AB===6,
∵AB=AD+BD,BD=BC=3,
∴AD=5﹣4=2.
23.解:(1)△A′B′C′如图所示;
(2)线段CC′被直线l垂直平分;
(3)△ABC的面积=2×4﹣×1×6﹣×2×6,
=8﹣1﹣2﹣2,
=8﹣8,
=3;
(4)点P如图所示.
故答案为:(2)垂直平分;(3)3.
24.解:△ABC是等腰直角三角形,
理由是:∵△ACE≌△BCD,
∴AC=BC,∠EAC=∠B,
∵AD2+DB2=DE5,
∴AD2+AE2=DE7,
∴∠EAD=90°,
∴∠EAC+∠DAC=90°,
∴∠DAC+∠B=90°,
∴∠ACB=180°﹣90°=90°,
∵AC=BC,
∴△ABC是等腰直角三角形.
25.解:(1)如图1中,
∵AB=AC,∠ABC=∠ACB=45°,∠ADE=∠AED=45°,
∴∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD+CD=CE+CD;
(2)不成立,存在的数量关系为CE=BC+CD.
理由:如图2,由(1)同理可得,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BD=BC+CD,
∴CE=BC+CD;
(3)如图5,结论:CD=BC+EC.
理由:由(1)同理可得,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CD=BC+BD=BC+CE,
第1页(共1页)
一、选择题(本题共10小题,共30分.在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,不选或选出的答案超过一个均记零分.)
1.(3分)下列选项中,线段BD是△ABC的高的是( )
A.
B.
C.
D.
2.(3分)从平面镜里看到背后墙上电子钟的示数如图所示,这时的正确时间是( )
A.21:05
B.21:15
C.20:15
D.20:12
3.(3分)下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
A.3,4,5
B.,,
C.30,40,50
D.0.3,0.4,0.5
4.(3分)如果三角形的两边分别为3和5,那么这个三角形的周长可能是( )
A.15
B.16
C.8
D.7
5.(3分)如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )
A.1
B.2
C.3
D.4
6.(3分)已知∠AOB,用尺规作一个角∠A′O′B′等于已知角∠AOB的作图痕迹如图所示,则判断∠A′O′B′=∠AOB所用到的三角形全等的判断方法是( )
A.SAS
B.ASA
C.AAS
D.SSS
7.(3分)如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )
A.∠B=∠E
B.∠BAD=∠EAC
C.∠BAC=∠EAD
D.BC=ED
8.(3分)已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A.25
B.7
C.5和7
D.25或7
9.(3分)如图,已知△ABC中,点D、E分别是边BC、AB的中点.若△ABC的面积等于8,则△BDE的面积等于( )
A.2
B.3
C.4
D.5
10.(3分)如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③FG∥AD;④∠AHC=60°;⑤△BFG是等边三角形;其中正确的有( )
A.2个
B.3个
C.4个
D.5个
二、填空题(11-14题,每小题3分,15-18题,每小题3分,共28分)
11.(3分)等腰三角形的两边长分别为4,8,则它的周长为
.
12.(3分)如图,AC=DC,BC=EC,请你添加一个适当的条件:
,使得△ABC≌△DEC.
13.(3分)如图,已知在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是
.
14.(3分)如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有
种.
15.(4分)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F.若△ABC的面积是28cm2,AB=20cm,AC=8cm,则DE=
cm.
16.(4分)如图,一圆柱体的底面周长为10cm,高BD为12cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程为
cm.
17.(4分)如图,在△ABC中,AB=AC,D,A,E三点都在一条直线上,且∠BDA=∠AEC=∠BAC,BD=3,CE=6,则DE的长为
.
18.(4分)如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,…,若∠A=70°,则∠An﹣1AnBn﹣1的度数为
.(用含n的代数式表示)
三、解答题(本大题共62分)
19.(6分)如图,已知∠1=∠2,∠B=∠D,求证:CB=CD.
20.(6分)如图,已知:BC∥EF,BC=EF,AE=DB,请判断DF与AC的位置关系,并说明理由.
21.(9分)如图所示的一块地,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m,求这块地的面积.
22.(9分)如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交线段AB于D;以点A为圆心,AD长为半径画弧,交线段AC于点E,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)设BC=3,AC=4.求AD的长.
23.(10分)如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与关于直线l成轴对称的△A′B′C′;
(2)线段CC′被直线l
;
(3)△ABC的面积为
;
(4)在直线l上找一点P,使PB+PC的长最短.
24.(10分)如图,D为AB上一点,△ACE≌△BCD,AD2+DB2=DE2,试判断△ABC的形状,并说明理由.
25.(12分)已知△ABC和△ADE都是等腰直角三角形,点D是直线BC上的一动点(点D不与B、C重合),连接CE.
(1)在图1中,当点D在边BC上时,求证:BC=CE+CD;
(2)在图2中,当点D在边BC的延长线上时,结论BC=CE+CD是否还成立?若不成立,请猜想BC、CE、CD之间存在的数量关系,并说明理由;
(3)在图3中,当点D在边BC的反向延长线上时,补全图形,不需写证明过程,直接写出BC、CE、CD之间存在的数量关系.
2020-2021学年山东省东营市垦利区七年级(上)期中数学试卷(五四学制)
试题解析
一、选择题(本题共10小题,共30分.在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,不选或选出的答案超过一个均记零分.)
1.解:线段BD是△ABC的高,则过点B作对边AC的垂线.
故选:D.
2.解:由图分析可得题中所给的“20:15”与“21:05”成轴对称,这时的时间应是21:05.
故选:A.
3.解:A、∵32+32=54,∴能组成直角三角形;
B、∵()2+32≠()4,∴不能组成直角三角形;
C、∵302+402=502,∴能组成直角三角形;
D、∵0.37+0.44=0.57,∴能组成直角三角形.
故选:B.
4.解:设三角形的第三边为x,则2<x<8.故选A.
5.解:
∵垂线段最短,
∴当PQ⊥OM时,PQ有最小值,
又∵OP平分∠MON,PA⊥ON,
∴PQ=PA=2,
故选:B.
6.解:如图,连接CD,
∵在△COD和△C′O′D′中
,
∴△COD≌△C'O'D'(SSS),
∴∠A'O'B'=∠AOB(全等三角形的对应角相等).
故选:D.
7.解:∵AB=AE,AC=AD,
∴当∠BAD=∠EAC或∠BAC=∠EAD,依据SAS即可得到△ABC≌△AED;
当BC=ED时,依据SSS即可得到△ABC≌△AED;
当∠B=∠E时,不能判定△ABC≌△AED.
故选:A.
8.解:分两种情况:
①当3和4为直角边长时,
由勾股定理得:第三边长的平方,即斜边长的平方=62+44=25;
②4为斜边长时,
由勾股定理得:第三边长的平方=46﹣32=2;
综上所述:第三边长的平方是25或7;
故选:D.
9.解:∵点D边BC的中点,△ABC的面积等于8,
∴S△ABD=S△ABC=4,
∵E是AB的中点,
∴S△BDE=S△ABD=2=2,
故选:A.
10.解:∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,
∴∠ABE=∠CBD,
即AB=BC,BD=BE
∴△ABE≌△CBD(SAS),
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60°,
∴△BGD≌△BFE(ASA),
∴BG=BF,∠BFG=∠BGF=60°,
∴∠BGF=∠EBD,
∴FG∥AD;
故①②③正确;
∵△ABE≌△CBD,
∴∠EAB=∠BCD,
∵∠CBA=60°,
∴∠AHC=∠CDB+∠EAB=∠CDB+∠BCD=∠CBA=60°,
故④正确;
∵BF=BG,∠FBG=60°,
∴△BFG是等边三角形,
故⑤正确.
故选:D.
二、填空题(11-14题,每小题3分,15-18题,每小题3分,共28分)
11.解:①当4为腰时,4+6=8;
②当8为腰时,4﹣4<8<3+4.
故此三角形的周长=8+4+4=20.
故答案是:20.
12.解:添加条件是:AB=DE,
在△ABC与△DEC中,,
∴△ABC≌△DEC.
故答案为:AB=DE.本题答案不唯一.
13.解:∵DE是BC的垂直平分线,
∴DB=DC,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=15,
故答案为:15.
14.解:如图,有三种方案,
故答案为3.
15.解:在△ABC中,AD为∠BAC的平分线,DF⊥AC于F,
∴DE=DF,
∴S△ABC=S△ABD+S△ACD=AB?DE+,
∵△ABC面积是28cm2,AB=20cm,AC=3cm,
∴×20DE+,
解得DE=2cm.
故答案为:7.
16.解:如图所示:
由于圆柱体的底面周长为10cm,
则AD=10×=5(cm).
又因为BD=AC=12cm,
所以DC===13(cm).
故蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程为13cm.
故答案为:13.
17.解:∵∠BDA=∠AEC=∠BAC,
∴∠DBA+∠BAD=∠BAD+∠CAE,
∴∠DBA=∠CAE,
∵在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AE+AD=BD+CE=3+6=6.
故答案为:9.
18.解:∵在△ABA1中,∠A=70°1B,
∴∠BA3A=70°,
∵A1A2=A8B1,∠BA1A是△A2A2B1的外角,
∴∠B3A2A1==35°;
同理可得,
∠B2A8A2=17.5°,∠B2A4A3=×17.5°=,
∴∠An﹣1AnBn﹣1=.
故答案为:.
三、解答题(本大题共62分)
19.证明:如图,∵∠1=∠2,
∴∠ACB=∠ACD.
在△ABC与△ADC中,
,
∴△ABC≌△ADC(AAS),
∴CB=CD.
20.解:结论:DF∥AC.
理由:∵AE=BD,
∴DE=AB,
∵EF∥BC,
∴∠E=∠B,
∵EF=BC,
∴△EFD≌△BCA,
∴∠DEF=∠BAC,
∴∠ADF=∠DAC,
∴DF∥AC.
21.解:连接AC.
∵AD=3 m,CD=4 m,
∴AC=m.
∵BC=12 m,AB=13 m,
∴BC2+AC2=125+52=169(m4),AB2=132=169(m3),
∴BC2+AC2=AB2,
∴∠ACB=90°.
∴S四边形ABCD=SRt△ADC+SRt△ABC
=
=
=36(m8).
故这块地的面积为36m2.
22.解:(1)∵∠ACD=90°,∠A=28°,
∴∠B=62°.
∵BD=BC,
∴∠BCD=∠BDC==59°.
∴∠ACD=90°﹣∠BCD=90°﹣59°=31°;
(2)∵∠ACB=90°,BC=3,
由勾股定理得:AB===6,
∵AB=AD+BD,BD=BC=3,
∴AD=5﹣4=2.
23.解:(1)△A′B′C′如图所示;
(2)线段CC′被直线l垂直平分;
(3)△ABC的面积=2×4﹣×1×6﹣×2×6,
=8﹣1﹣2﹣2,
=8﹣8,
=3;
(4)点P如图所示.
故答案为:(2)垂直平分;(3)3.
24.解:△ABC是等腰直角三角形,
理由是:∵△ACE≌△BCD,
∴AC=BC,∠EAC=∠B,
∵AD2+DB2=DE5,
∴AD2+AE2=DE7,
∴∠EAD=90°,
∴∠EAC+∠DAC=90°,
∴∠DAC+∠B=90°,
∴∠ACB=180°﹣90°=90°,
∵AC=BC,
∴△ABC是等腰直角三角形.
25.解:(1)如图1中,
∵AB=AC,∠ABC=∠ACB=45°,∠ADE=∠AED=45°,
∴∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BC=BD+CD=CE+CD;
(2)不成立,存在的数量关系为CE=BC+CD.
理由:如图2,由(1)同理可得,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴BD=BC+CD,
∴CE=BC+CD;
(3)如图5,结论:CD=BC+EC.
理由:由(1)同理可得,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CD=BC+BD=BC+CE,
第1页(共1页)
同课章节目录
