人教版九年级数学上册 24.3.1圆周角(共14张ppt)
文档属性
| 名称 | 人教版九年级数学上册 24.3.1圆周角(共14张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 248.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 05:59:41 | ||
图片预览


文档简介
(共14张PPT)
24.3.1
圆周角
一.
复习引入:
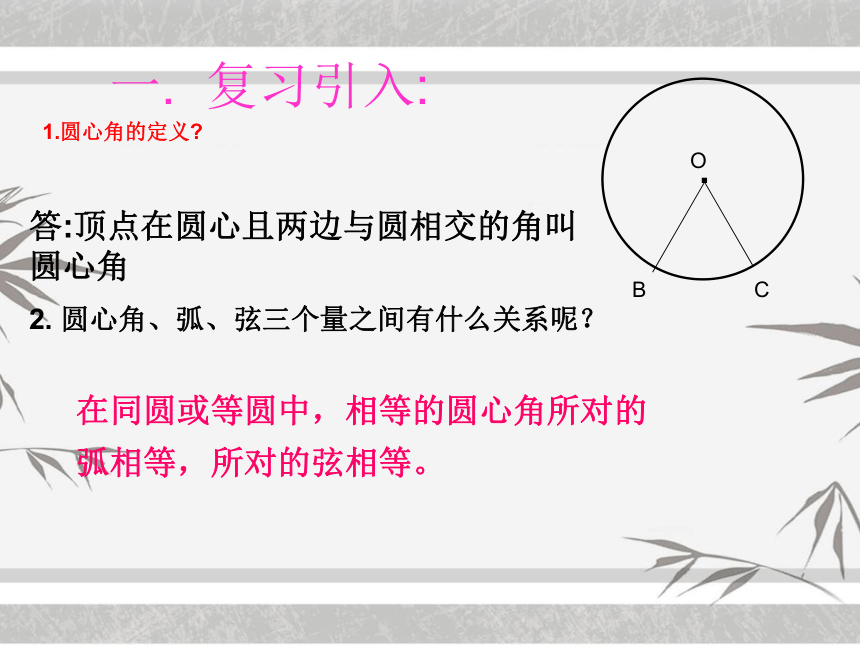
1.圆心角的定义?
.
O
B
C
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
答:顶点在圆心且两边与圆相交的角叫圆心角
2.
圆心角、弧、弦三个量之间有什么关系呢?
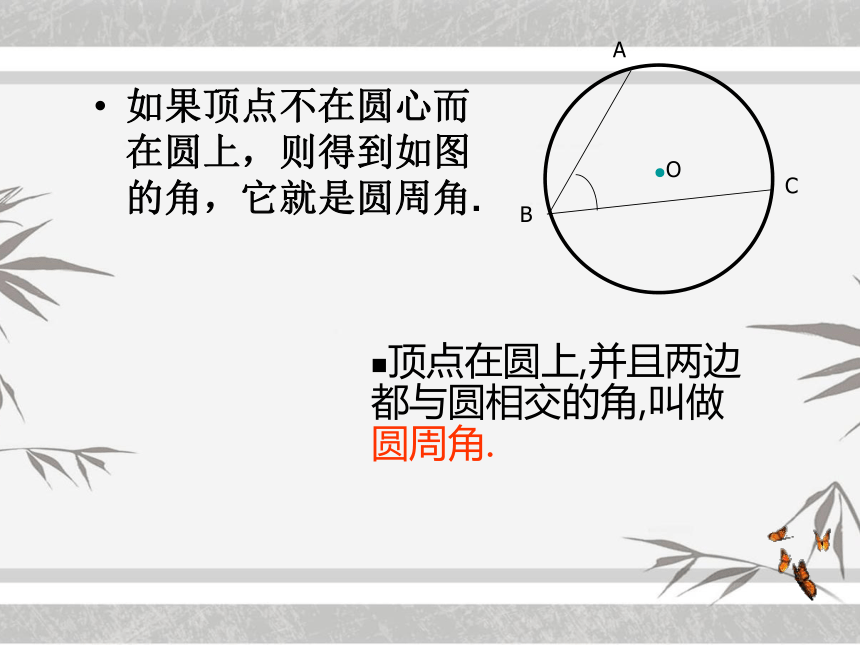
如果顶点不在圆心而在圆上,则得到如图的角,它就是圆周角.
顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
●O
B
A
C
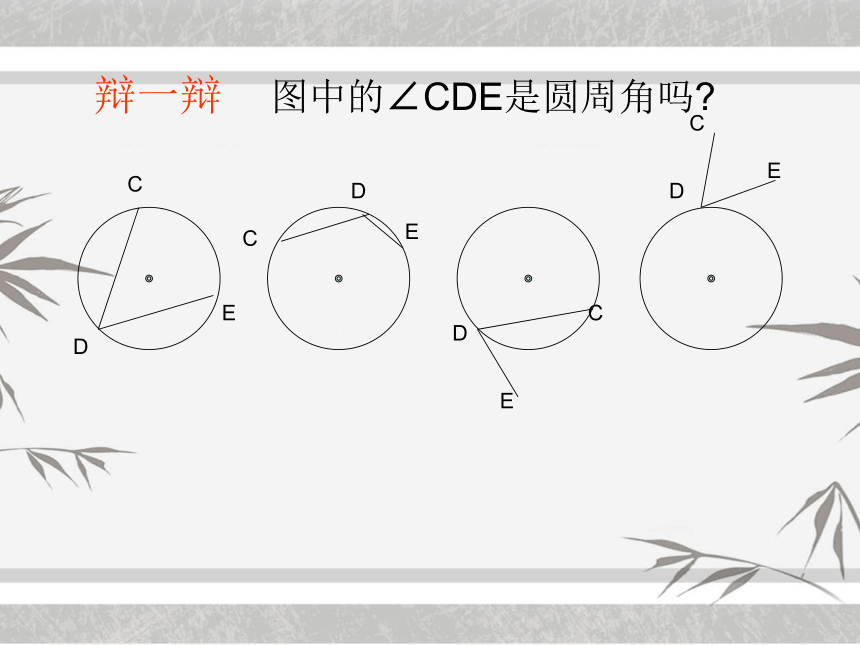
辩一辩
图中的∠CDE是圆周角吗?
C
D
E
C
D
E
C
D
E
C
D
E
类比圆心角探知圆周角
在同圆或等圆中,同弧或等弧所对的圆心角相等.
在同圆或等圆中,同弧或等弧所对的圆周角有什么关系?圆周角和圆心角之间又有什么关系呢?
为了解决这个问题,我们先探究同弧所对的圆周角和圆心角之间有的关系.
你会画同弧所对的圆周角和圆心角吗?
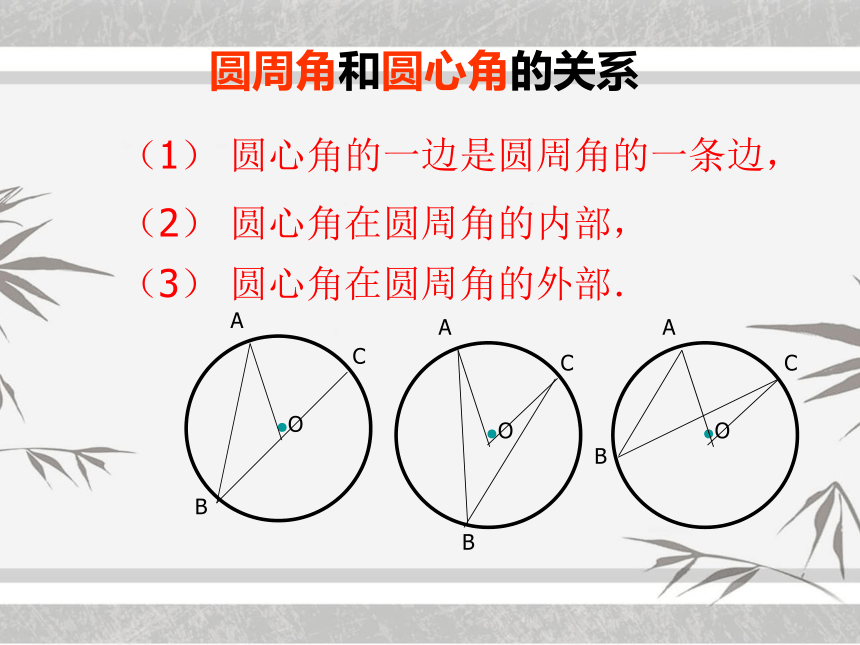
圆周角和圆心角的关系
(1)
圆心角的一边是圆周角的一条边,
(2)
圆心角在圆周角的内部,
(3)
圆心角在圆周角的外部.
●O
A
B
C
●O
A
B
C
●O
A
B
C
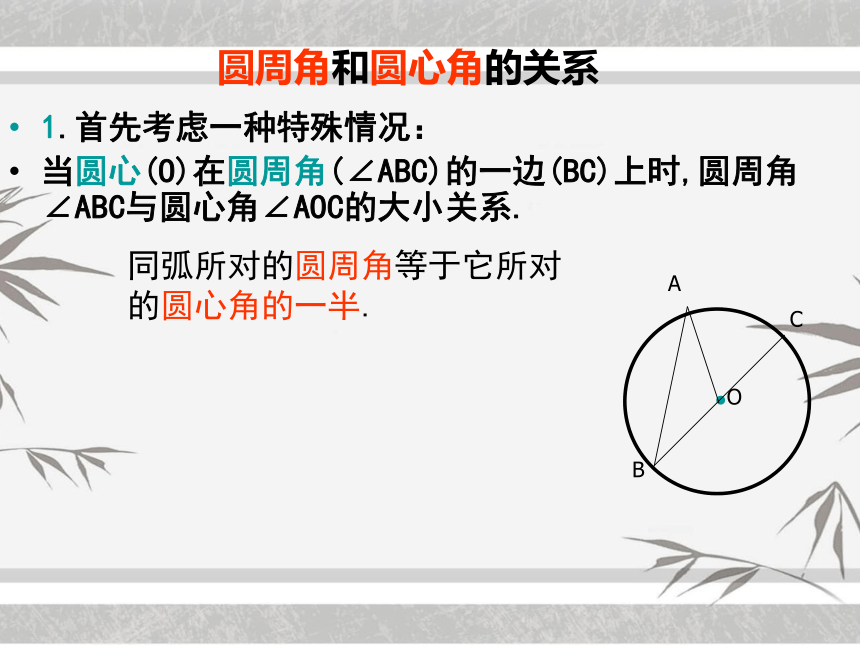
圆周角和圆心角的关系
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
●O
A
B
C
同弧所对的圆周角等于它所对的圆心角的一半.
O
A
B
D
O
A
C
D
O
A
B
C
D
圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
圆心O在∠BAC的外部
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
同弧所对的圆周角等于它所对的圆心角的一半.
即
∠ABC
=
∠AOC.
●O
A
B
C
●O
A
B
C
●O
A
B
C
如图所示,∠ADB、∠ACB、∠AOB
分别是什么角?
它们
有何共同点?
∠ADB与∠ACB有什么关系?
同弧
所对的圆周角相等.
(等弧)
思考:
相等的圆周角所对的弧相等吗?
在同圆或等圆中
都等于这条弧所对的圆心角的一半.
圆周角定理:
1.试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠2=∠7
∠1=∠4
∠3=∠6
∠5=∠8
A
B
O
C
2、如图,AB是直径,则∠ACB=___
90
度
半圆(或直径)所对的圆周角是直角,
90度的圆周角所对的弦是直径。
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
课堂小结
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
1.90°的圆周角所对的弦是直径;
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
圆周角与直
线的关系
半圆或直径所对的圆周角都相等,都等于90°(直角).
24.3.1
圆周角
一.
复习引入:
1.圆心角的定义?
.
O
B
C
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
答:顶点在圆心且两边与圆相交的角叫圆心角
2.
圆心角、弧、弦三个量之间有什么关系呢?
如果顶点不在圆心而在圆上,则得到如图的角,它就是圆周角.
顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
●O
B
A
C
辩一辩
图中的∠CDE是圆周角吗?
C
D
E
C
D
E
C
D
E
C
D
E
类比圆心角探知圆周角
在同圆或等圆中,同弧或等弧所对的圆心角相等.
在同圆或等圆中,同弧或等弧所对的圆周角有什么关系?圆周角和圆心角之间又有什么关系呢?
为了解决这个问题,我们先探究同弧所对的圆周角和圆心角之间有的关系.
你会画同弧所对的圆周角和圆心角吗?
圆周角和圆心角的关系
(1)
圆心角的一边是圆周角的一条边,
(2)
圆心角在圆周角的内部,
(3)
圆心角在圆周角的外部.
●O
A
B
C
●O
A
B
C
●O
A
B
C
圆周角和圆心角的关系
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
●O
A
B
C
同弧所对的圆周角等于它所对的圆心角的一半.
O
A
B
D
O
A
C
D
O
A
B
C
D
圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
圆心O在∠BAC的外部
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
同弧所对的圆周角等于它所对的圆心角的一半.
即
∠ABC
=
∠AOC.
●O
A
B
C
●O
A
B
C
●O
A
B
C
如图所示,∠ADB、∠ACB、∠AOB
分别是什么角?
它们
有何共同点?
∠ADB与∠ACB有什么关系?
同弧
所对的圆周角相等.
(等弧)
思考:
相等的圆周角所对的弧相等吗?
在同圆或等圆中
都等于这条弧所对的圆心角的一半.
圆周角定理:
1.试找出下图中所有相等的圆周角。
A
B
C
D
1
2
3
4
5
6
7
8
∠2=∠7
∠1=∠4
∠3=∠6
∠5=∠8
A
B
O
C
2、如图,AB是直径,则∠ACB=___
90
度
半圆(或直径)所对的圆周角是直角,
90度的圆周角所对的弦是直径。
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
课堂小结
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
1.90°的圆周角所对的弦是直径;
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
圆周角与直
线的关系
半圆或直径所对的圆周角都相等,都等于90°(直角).
同课章节目录
