27.2.2 相似三角形的性质(共15张ppt)
文档属性
| 名称 | 27.2.2 相似三角形的性质(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 998.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
27.2.2
相似三角形的性质
人教版·九年级数学·下册
1.理解并掌握相似三角形对应高的比、对应角平分线的比、对应中线的比等于相似比,并能用来解题.
2.理解并掌握相似三角形周长的比等于相似比,面积比等于相似比的平方的性质,并能用来解决简单的问题.
重点:相似三角形的性质及其运用.
难点:探索相似三角形周长的比、对应线段比等于相似比、面积比等于相似比的平方.
阅读课本P37-38页内容,了解本节主要内容.
角平分线
中线
相似比
比的平方
高
相似比
1.什么叫相似三角形?什么叫相似比?
2.相似三角形有哪些判定方法?
根据相似三角形的概念,如果两个三角形相似,它们对应边的比一定等于相似比,那么相似三角形还有哪些性质呢?这节课我们就来研究这个问题.
探究1:相似三角形的对应线段
已知△ABC∽△A′B′C′,△ABC与△A′B′C′的相似比为k,它们对应高的比是多少?对应角平分线的比是多少?对应中线的比呢?你能证明你的结论吗?
归纳:
相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
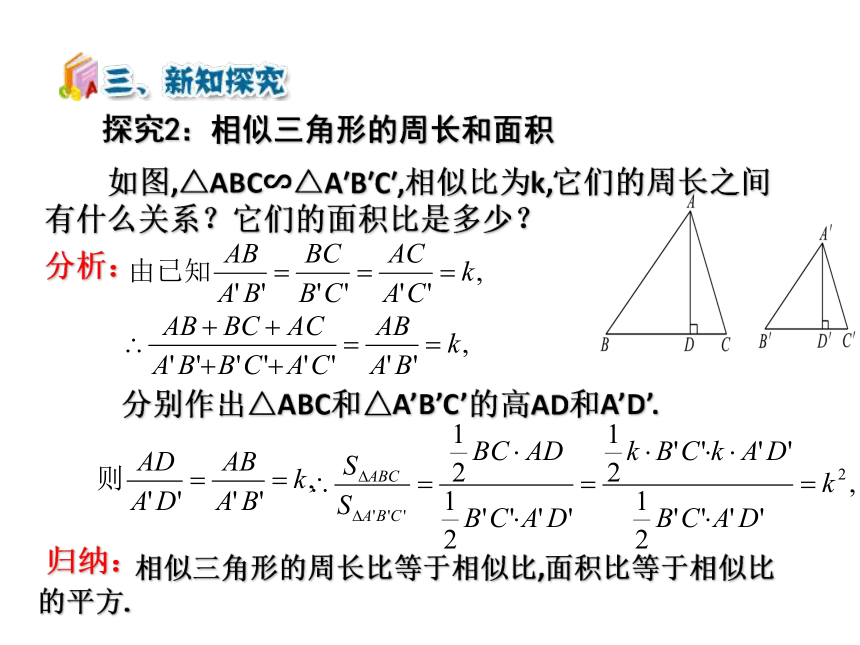
探究2:相似三角形的周长和面积
分别作出△ABC和△A’B’C’的高AD和A’D’.
如图,△ABC∽△A′B′C′,相似比为k,它们的周长之间有什么关系?它们的面积比是多少?
分析:
归纳:
相似三角形的周长比等于相似比,面积比等于相似比的平方.
例1:如图所示,△ABC中,BC=48,高AD=16,它的内接矩形的两邻边EF∶FM=5∶9,长边MF在BC边上,求矩形EFMN的面积.
解析:
因为EF∶FM=5∶9,∴设EF=5x,FM=9x,
解:
∴EN=9x=18,EF=5x=10,
因为EF∶FM=5∶9,可设EF=5x,FM=9x,根据相似三角形的性质,可求出矩形的两邻边长.
∵AD=16,∴AP=AD-PD=16-5x,
由EN∥BC,得△AEN∽△ABC,
∴S矩形EFMN=18×10=180.
例2:如图所示,D、E分别是△ABC的边AB、
AC的中点,M是DE的中点,CM的延长线交AB于点
N,则S△DMN∶S四边形ANME的值为多少?
连接DC.
解:
∵点D、E分别是AB、AC的中点,
∴△ADE∽△ABC,△NDM∽△NBC.
设S△EMC=a,则S△DMC=S△EMC=a,
∴S△EDC=2S△EMC=2a.
∴DE∥BC.
1:2
B
B
解:
(1)∵DC=AC,∴△ACD为等腰三角形.
9.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,
∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.
(1)求证:EF∥BC;
(2)若四边形BDFE的面积为6,求△ABD的面积.
又∵CF平分∠ACD,∴F为AD的中点,
又E为AB的中点,∴EF为△ABD的中位线,
∴EF∥BC.
(2)设△ABD的面积为x,
由EF为△ABC中位线可知△AEF∽△ABD,且
∴x=8,即△ABD的面积为8.
1.通过这节课同学们学到了什么?
(1)相似三角形的对应高的比、对应角平分线的比、对应中线的比都等于相似比,周长比等于相似比.
(2)相似三角形面积的比等于相似比的平方.
2.对本节课你有什么困惑?
27.2.2
相似三角形的性质
人教版·九年级数学·下册
1.理解并掌握相似三角形对应高的比、对应角平分线的比、对应中线的比等于相似比,并能用来解题.
2.理解并掌握相似三角形周长的比等于相似比,面积比等于相似比的平方的性质,并能用来解决简单的问题.
重点:相似三角形的性质及其运用.
难点:探索相似三角形周长的比、对应线段比等于相似比、面积比等于相似比的平方.
阅读课本P37-38页内容,了解本节主要内容.
角平分线
中线
相似比
比的平方
高
相似比
1.什么叫相似三角形?什么叫相似比?
2.相似三角形有哪些判定方法?
根据相似三角形的概念,如果两个三角形相似,它们对应边的比一定等于相似比,那么相似三角形还有哪些性质呢?这节课我们就来研究这个问题.
探究1:相似三角形的对应线段
已知△ABC∽△A′B′C′,△ABC与△A′B′C′的相似比为k,它们对应高的比是多少?对应角平分线的比是多少?对应中线的比呢?你能证明你的结论吗?
归纳:
相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
探究2:相似三角形的周长和面积
分别作出△ABC和△A’B’C’的高AD和A’D’.
如图,△ABC∽△A′B′C′,相似比为k,它们的周长之间有什么关系?它们的面积比是多少?
分析:
归纳:
相似三角形的周长比等于相似比,面积比等于相似比的平方.
例1:如图所示,△ABC中,BC=48,高AD=16,它的内接矩形的两邻边EF∶FM=5∶9,长边MF在BC边上,求矩形EFMN的面积.
解析:
因为EF∶FM=5∶9,∴设EF=5x,FM=9x,
解:
∴EN=9x=18,EF=5x=10,
因为EF∶FM=5∶9,可设EF=5x,FM=9x,根据相似三角形的性质,可求出矩形的两邻边长.
∵AD=16,∴AP=AD-PD=16-5x,
由EN∥BC,得△AEN∽△ABC,
∴S矩形EFMN=18×10=180.
例2:如图所示,D、E分别是△ABC的边AB、
AC的中点,M是DE的中点,CM的延长线交AB于点
N,则S△DMN∶S四边形ANME的值为多少?
连接DC.
解:
∵点D、E分别是AB、AC的中点,
∴△ADE∽△ABC,△NDM∽△NBC.
设S△EMC=a,则S△DMC=S△EMC=a,
∴S△EDC=2S△EMC=2a.
∴DE∥BC.
1:2
B
B
解:
(1)∵DC=AC,∴△ACD为等腰三角形.
9.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,
∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.
(1)求证:EF∥BC;
(2)若四边形BDFE的面积为6,求△ABD的面积.
又∵CF平分∠ACD,∴F为AD的中点,
又E为AB的中点,∴EF为△ABD的中位线,
∴EF∥BC.
(2)设△ABD的面积为x,
由EF为△ABC中位线可知△AEF∽△ABD,且
∴x=8,即△ABD的面积为8.
1.通过这节课同学们学到了什么?
(1)相似三角形的对应高的比、对应角平分线的比、对应中线的比都等于相似比,周长比等于相似比.
(2)相似三角形面积的比等于相似比的平方.
2.对本节课你有什么困惑?
