27.2.2 相似三角形应用举例(共16张ppt)
文档属性
| 名称 | 27.2.2 相似三角形应用举例(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
27.2.2
相似三角形应用举例
人教版·九年级数学·下册
1.进一步巩固相似三角形的知识.
2.能够运用三角形相似的知识,解决求不能直接测量物体的长度和高度(如测量金字塔高度问题、测量河宽问题)等一些实际问题.
重点:运用三角形相似的知识计算不能直接测量物体的长度和高度.
难点:灵活运用三角形相似的知识解决实际问题(如何把实际问题抽象为数学问题).
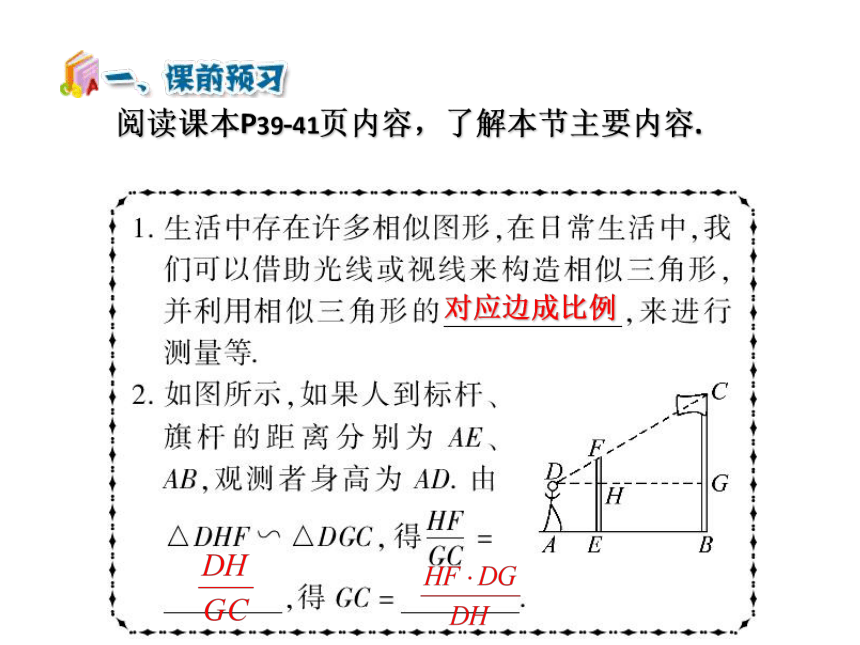
阅读课本P39-41页内容,了解本节主要内容.
对应边成比例
1.你看过或听说过解密埃及金字塔的故事吗?神秘的金字塔引来无数游客观光旅游,据史料记载,古希腊数学家、天文学家
泰勒斯曾用相似三
角形的原理测量出
金字塔的高度,他是
怎样求出金字塔的
高度的?
2.阳光不仅孕育着万物生长,而且还能成为数学计算的工具,你能设计出借助来自太阳的光线来测量金字塔的方案吗?试与其他同学交流.
3.我们曾利用三角形全等的方法测距离,想一想,我们能否利用相似三角形的有关知识来测量物体的高度或物体的距离呢?试与其他同学交流.
探究1:利用太阳光或平面镜测高
利用相似三角形的知识解决实际问题的关键是构造相似三角形数学模型,数据模型有:
(1)利用“同一时刻的物高和影长对应成比例”构造相似三角形.
(2)利用“标杆在测量中的作用”构造相似三角形.
(3)利用“平面镜的反射原理”构造相似三角形.
相似图形模型有:
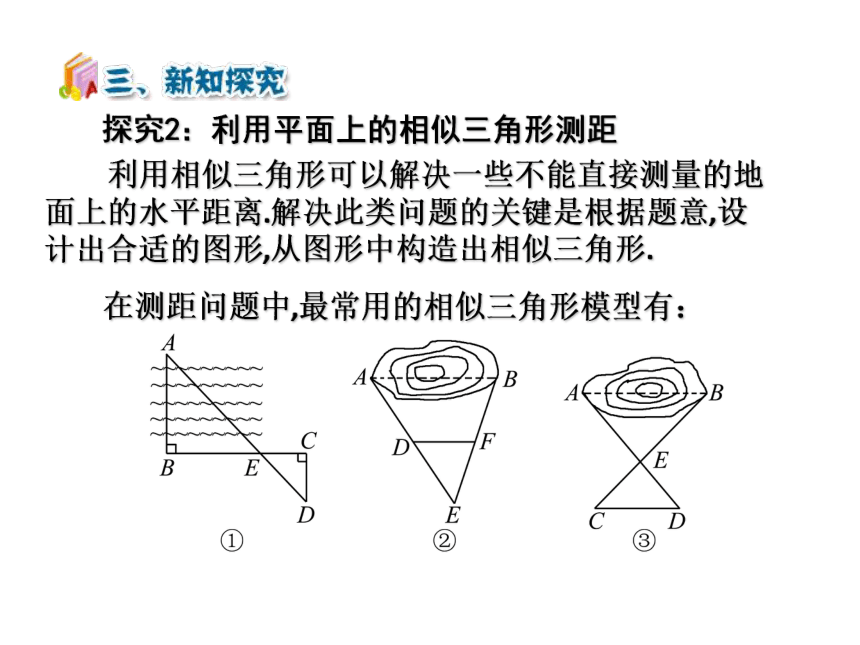
探究2:利用平面上的相似三角形测距
在测距问题中,最常用的相似三角形模型有:
利用相似三角形可以解决一些不能直接测量的地面上的水平距离.解决此类问题的关键是根据题意,设计出合适的图形,从图形中构造出相似三角形.
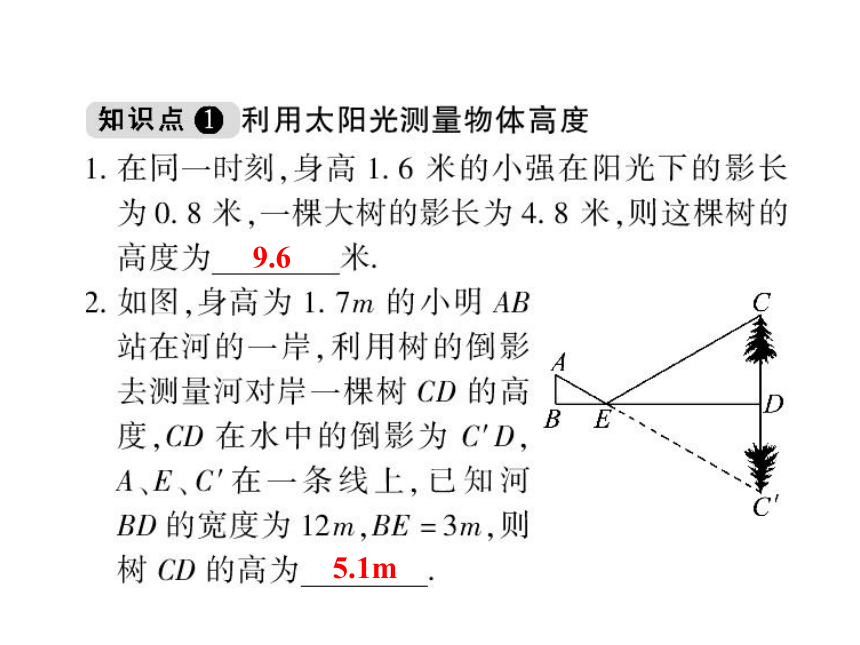
9.6
5.1m
70
B
例1:小玲用下面的方法来测量学校教学大楼AB的高度.如图所示,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=21m,当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面的高度DC=1.6m,请你帮助小玲计算出教学大楼的高度AB.
(根据光的反射定律:反射角等于入射角)
解析:
根据反射角等于入射角有∠DEF=∠BEF,而FE⊥AC,
解:
由反射角等于入射角有∠DEF=∠BEF,而FE⊥AC,∴∠DEC=∠BEA,可得出△DEC∽△BEA,从而求出AB的高度.
∴∠DEC=∠BEA.
又∵∠DCE=∠BAE=90°,∴△DEC∽△BEA,
∵DC=1.6,EC=2.5,EA=21,
∴AB=13.44.即建筑物AB的高度为13.44m.
例1:小玲用下面的方法来测量学校教学大楼AB的高度.如图所示,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=21m,当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面的高度DC=1.6m,请你帮助小玲计算出教学大楼的高度AB.
(根据光的反射定律:反射角等于入射角)
解析:
从实际问题的情景中找出相似三角形是解决本类题型的关键.
点评:
由反射角等于入射角有∠DEF=∠BEF,而FE⊥AC,∴∠DEC=∠BEA,可得出△DEC∽△BEA,从而求出AB的高度.
例2:如图所示,有一池塘,要测量两端A、B的
距离,可先在平地上取一个可以直接到达A和B的点
C,连接AC并延长到点D,使CD=
CA,连接BC并延长
到点E,使CE=
CB,连接ED,如果测量出DE的长为25m,
那么池塘宽AB是多少?为什么?
解析:
由题中的条件可得△ABC∽△DEC,由相似三角形的对应边的比相等可求出AB的值.
AB=50m.
解:
又∵∠ACB=∠DCE,∴△CAB∽△CDE,
∵DE=25m,∴AB=50m.
1.5m
48m
C
16
解:
作AH⊥EF,垂足为H,交CD于点G,
9.
小强同学所在的学习小组欲测量学校里一棵大树的高度,他们选小强作为观测者,并在小强与大树之间的地面上直立一根2m的标杆CD,然后小强开始调整自己的位置,当他看到标杆的顶端C与树的顶端E重合时,就在该位置停止不动,这时其他同学通过测量,发现小强的脚与标杆的底部距离
BD为1m,离大树底部距离BF为9m,小强的眼睛离
地面的高度AB为1.5m,求这棵大树的高度.
由题意知AB⊥BF,CD⊥BF,EF⊥BF,
所以四边形ABFH、四边形DGHF都是矩形,
所以AB=GD=HF=1.5m,BF=AH=9m,BD=AG=1m,
因为CD∥EF,所以∠AGC=∠AHE=90°,
又因为∠CAG=∠EAH,所以△ACG∽△AEH,
所以EF=EH+HF=4.5+1.5=6(m),所以这棵树的高度为6m.
相似三
角形应
用举例
测量物体
的高度
测量无法到达顶部的
物体的高度时,通常
利用“在同一时刻物
体高与影长成比例”
的原理解决
测量河宽
构造相似三角形
27.2.2
相似三角形应用举例
人教版·九年级数学·下册
1.进一步巩固相似三角形的知识.
2.能够运用三角形相似的知识,解决求不能直接测量物体的长度和高度(如测量金字塔高度问题、测量河宽问题)等一些实际问题.
重点:运用三角形相似的知识计算不能直接测量物体的长度和高度.
难点:灵活运用三角形相似的知识解决实际问题(如何把实际问题抽象为数学问题).
阅读课本P39-41页内容,了解本节主要内容.
对应边成比例
1.你看过或听说过解密埃及金字塔的故事吗?神秘的金字塔引来无数游客观光旅游,据史料记载,古希腊数学家、天文学家
泰勒斯曾用相似三
角形的原理测量出
金字塔的高度,他是
怎样求出金字塔的
高度的?
2.阳光不仅孕育着万物生长,而且还能成为数学计算的工具,你能设计出借助来自太阳的光线来测量金字塔的方案吗?试与其他同学交流.
3.我们曾利用三角形全等的方法测距离,想一想,我们能否利用相似三角形的有关知识来测量物体的高度或物体的距离呢?试与其他同学交流.
探究1:利用太阳光或平面镜测高
利用相似三角形的知识解决实际问题的关键是构造相似三角形数学模型,数据模型有:
(1)利用“同一时刻的物高和影长对应成比例”构造相似三角形.
(2)利用“标杆在测量中的作用”构造相似三角形.
(3)利用“平面镜的反射原理”构造相似三角形.
相似图形模型有:
探究2:利用平面上的相似三角形测距
在测距问题中,最常用的相似三角形模型有:
利用相似三角形可以解决一些不能直接测量的地面上的水平距离.解决此类问题的关键是根据题意,设计出合适的图形,从图形中构造出相似三角形.
9.6
5.1m
70
B
例1:小玲用下面的方法来测量学校教学大楼AB的高度.如图所示,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=21m,当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面的高度DC=1.6m,请你帮助小玲计算出教学大楼的高度AB.
(根据光的反射定律:反射角等于入射角)
解析:
根据反射角等于入射角有∠DEF=∠BEF,而FE⊥AC,
解:
由反射角等于入射角有∠DEF=∠BEF,而FE⊥AC,∴∠DEC=∠BEA,可得出△DEC∽△BEA,从而求出AB的高度.
∴∠DEC=∠BEA.
又∵∠DCE=∠BAE=90°,∴△DEC∽△BEA,
∵DC=1.6,EC=2.5,EA=21,
∴AB=13.44.即建筑物AB的高度为13.44m.
例1:小玲用下面的方法来测量学校教学大楼AB的高度.如图所示,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=21m,当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面的高度DC=1.6m,请你帮助小玲计算出教学大楼的高度AB.
(根据光的反射定律:反射角等于入射角)
解析:
从实际问题的情景中找出相似三角形是解决本类题型的关键.
点评:
由反射角等于入射角有∠DEF=∠BEF,而FE⊥AC,∴∠DEC=∠BEA,可得出△DEC∽△BEA,从而求出AB的高度.
例2:如图所示,有一池塘,要测量两端A、B的
距离,可先在平地上取一个可以直接到达A和B的点
C,连接AC并延长到点D,使CD=
CA,连接BC并延长
到点E,使CE=
CB,连接ED,如果测量出DE的长为25m,
那么池塘宽AB是多少?为什么?
解析:
由题中的条件可得△ABC∽△DEC,由相似三角形的对应边的比相等可求出AB的值.
AB=50m.
解:
又∵∠ACB=∠DCE,∴△CAB∽△CDE,
∵DE=25m,∴AB=50m.
1.5m
48m
C
16
解:
作AH⊥EF,垂足为H,交CD于点G,
9.
小强同学所在的学习小组欲测量学校里一棵大树的高度,他们选小强作为观测者,并在小强与大树之间的地面上直立一根2m的标杆CD,然后小强开始调整自己的位置,当他看到标杆的顶端C与树的顶端E重合时,就在该位置停止不动,这时其他同学通过测量,发现小强的脚与标杆的底部距离
BD为1m,离大树底部距离BF为9m,小强的眼睛离
地面的高度AB为1.5m,求这棵大树的高度.
由题意知AB⊥BF,CD⊥BF,EF⊥BF,
所以四边形ABFH、四边形DGHF都是矩形,
所以AB=GD=HF=1.5m,BF=AH=9m,BD=AG=1m,
因为CD∥EF,所以∠AGC=∠AHE=90°,
又因为∠CAG=∠EAH,所以△ACG∽△AEH,
所以EF=EH+HF=4.5+1.5=6(m),所以这棵树的高度为6m.
相似三
角形应
用举例
测量物体
的高度
测量无法到达顶部的
物体的高度时,通常
利用“在同一时刻物
体高与影长成比例”
的原理解决
测量河宽
构造相似三角形
