六年级数学下册课件-3.1 第8课时 圆柱的体积(练习课)-人教版(15张PPT)
文档属性
| 名称 | 六年级数学下册课件-3.1 第8课时 圆柱的体积(练习课)-人教版(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览





文档简介
3
圆柱与圆锥
1 圆 柱
第8课时 圆柱的体积(练习课)
一、基础练习
6、求下面图形的表面积和体积。(单位:cm)
(1)表面积:3.14×6×12+3.14×(6÷2)2×2
= 282.6(cm2)
体积: 3.14×(6÷2)2×12
= 339.12(cm3)
(2)表面积:(15×20+15×10+10×20)×2
= 1300(cm2)
体积: 15×10×20
= 3000(cm3)
体积: 3.14×(14÷2)2×5
= 769.3(cm3)
(3)表面积:3.14×14×5+3.14×(14÷2)2×2
= 527.52(cm2)
练
习
五
圆柱的体积= 底面积 × 高
V =Sh
一、基础练习
2、如图,这个圆柱形水桶可以装多少水?
60cm
3.14×(60÷2)2×90
= 254340(cm3)
答:这个圆柱形水桶可以装254.34 L的水。
254340 cm3 =254340 mL=254.34 L
练
习
五
7、学校要在教学区和操场之间修一道围墙,原计划用土石35m?。后来多开了一个厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米土石?
答:现在用了34.215 m3的土石。
先求一个底面直径为2m、高为0.25m的圆柱的体积。
35-3.14×(2÷2)2×0.25
=35-3.14×1×0.25
=35-0.785
=34.215(m?)
二、指导练习
25 cm=0.25 m
练
习
五
二、指导练习
9、两个底面积相等的圆柱,一个高为4.5dm,体积为81dm3。另一个高为3dm,它的体积是多少?
81÷4.5×3=54(dm3)
答:另一个圆柱的体积是54dm3。
只要求出其中一个圆柱的底面积,也就得出了另一个圆柱的底面积。
圆柱的底面积=体积÷高
圆柱的体积=底面积×高
练
习
五
二、指导练习
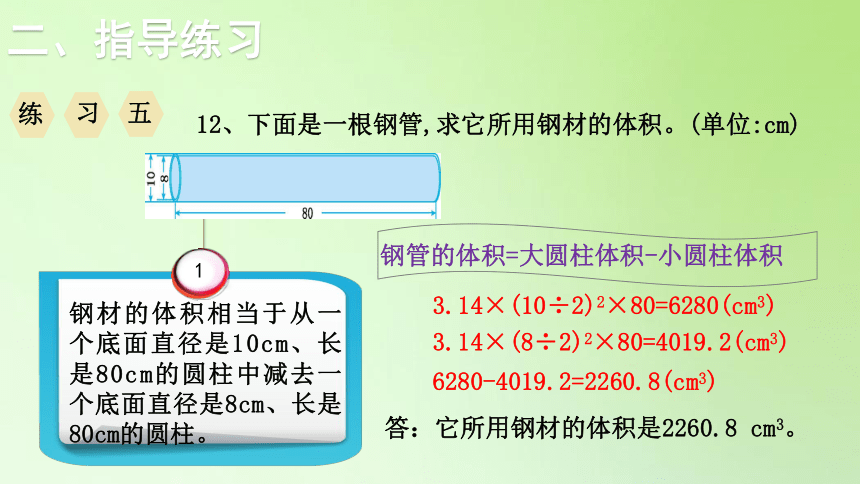
钢材的体积相当于从一个底面直径是10cm、长是80cm的圆柱中减去一个底面直径是8cm、长是80cm的圆柱。
1
3.14×(10÷2)2×80=6280(cm3)
3.14×(8÷2)2×80=4019.2(cm3)
6280-4019.2=2260.8(cm3)
12、下面是一根钢管,求它所用钢材的体积。(单位:cm)
钢管的体积=大圆柱体积-小圆柱体积
答:它所用钢材的体积是2260.8 cm3。
练
习
五
2
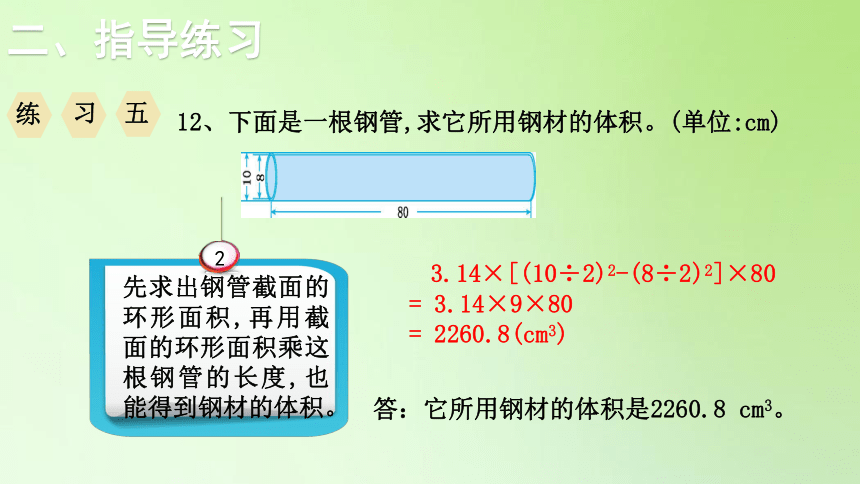
先求出钢管截面的环形面积,再用截面的环形面积乘这根钢管的长度,也能得到钢材的体积。
3.14×[(10÷2)2-(8÷2)2]×80
= 3.14×9×80
= 2260.8(cm3)
12、下面是一根钢管,求它所用钢材的体积。(单位:cm)
答:它所用钢材的体积是2260.8 cm3。
二、指导练习
练
习
五
三、巩固练习
14、右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?
20cm
10cm
以长为轴旋转,得到圆柱的底面半径是10cm,高20cm。
3.14×10?×20
=3.14×100×20
=314×20
=6280(cm?)
答:以长为轴旋转一周,得到的圆柱的体积是6280 cm3。
练
习
五
三、巩固练习
20cm
10cm
以宽为轴旋转,得到圆柱的底面半径是20cm,高10cm。
3.14×20?×10
=3.14×400×10
=1256×10
=12560(cm?)
答:以宽为轴旋转一周,得到的圆柱的体积是12560 cm3。
练
习
五
14、右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?
三、巩固练习
15、下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
图1
图2
图3
图4
18
12
9
6
2
3
4
6
观察
对比
上面4个长方形,从左到右,长不断变短,宽不断增长;长和宽的差也不断减小。
练
习
五
三、巩固练习
15、下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
图1
图2
图3
图4
18
12
9
6
2
3
4
6
图1的体积最大。
以长方形的长为底面周长。
图1:π×(18÷π÷2)2×2= (dm3)
图2:π×(12÷π÷2)2×3= (dm3)
图3:π×(9÷π÷2)2×4= (dm3)
图4:π×(6÷π÷2)2×6= (dm3)
> > >
练
习
五
三、巩固练习
15、下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
图1
图2
图3
图4
18
12
9
6
2
3
4
6
图4的体积最大。
以长方形的宽为底面周长。
图1:π×(2÷π÷2)2×18= (dm3)
图2:π×(3÷π÷2)2×12= (dm3)
图3:π×(4÷π÷2)2×9= (dm3)
图4:π×(6÷π÷2)2×6= (dm3)
> > >
练
习
五
用长方形卷成圆柱,以宽为圆柱的高卷成的圆柱体积最大。
1
圆柱的侧面积一定时,作为圆柱底面周长的边越长,体积越大。
2
15、下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
图1
图4
18
12
9
6
2
3
4
6
三、巩固练习
练
习
五
图2
图3
四、课堂小结
通过本节课的学习,你有什么收获?
作业:
五、作业布置
圆柱与圆锥
1 圆 柱
第8课时 圆柱的体积(练习课)
一、基础练习
6、求下面图形的表面积和体积。(单位:cm)
(1)表面积:3.14×6×12+3.14×(6÷2)2×2
= 282.6(cm2)
体积: 3.14×(6÷2)2×12
= 339.12(cm3)
(2)表面积:(15×20+15×10+10×20)×2
= 1300(cm2)
体积: 15×10×20
= 3000(cm3)
体积: 3.14×(14÷2)2×5
= 769.3(cm3)
(3)表面积:3.14×14×5+3.14×(14÷2)2×2
= 527.52(cm2)
练
习
五
圆柱的体积= 底面积 × 高
V =Sh
一、基础练习
2、如图,这个圆柱形水桶可以装多少水?
60cm
3.14×(60÷2)2×90
= 254340(cm3)
答:这个圆柱形水桶可以装254.34 L的水。
254340 cm3 =254340 mL=254.34 L
练
习
五
7、学校要在教学区和操场之间修一道围墙,原计划用土石35m?。后来多开了一个厚度为25cm的月亮门,减少了土石的用量。现在用了多少立方米土石?
答:现在用了34.215 m3的土石。
先求一个底面直径为2m、高为0.25m的圆柱的体积。
35-3.14×(2÷2)2×0.25
=35-3.14×1×0.25
=35-0.785
=34.215(m?)
二、指导练习
25 cm=0.25 m
练
习
五
二、指导练习
9、两个底面积相等的圆柱,一个高为4.5dm,体积为81dm3。另一个高为3dm,它的体积是多少?
81÷4.5×3=54(dm3)
答:另一个圆柱的体积是54dm3。
只要求出其中一个圆柱的底面积,也就得出了另一个圆柱的底面积。
圆柱的底面积=体积÷高
圆柱的体积=底面积×高
练
习
五
二、指导练习
钢材的体积相当于从一个底面直径是10cm、长是80cm的圆柱中减去一个底面直径是8cm、长是80cm的圆柱。
1
3.14×(10÷2)2×80=6280(cm3)
3.14×(8÷2)2×80=4019.2(cm3)
6280-4019.2=2260.8(cm3)
12、下面是一根钢管,求它所用钢材的体积。(单位:cm)
钢管的体积=大圆柱体积-小圆柱体积
答:它所用钢材的体积是2260.8 cm3。
练
习
五
2
先求出钢管截面的环形面积,再用截面的环形面积乘这根钢管的长度,也能得到钢材的体积。
3.14×[(10÷2)2-(8÷2)2]×80
= 3.14×9×80
= 2260.8(cm3)
12、下面是一根钢管,求它所用钢材的体积。(单位:cm)
答:它所用钢材的体积是2260.8 cm3。
二、指导练习
练
习
五
三、巩固练习
14、右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?
20cm
10cm
以长为轴旋转,得到圆柱的底面半径是10cm,高20cm。
3.14×10?×20
=3.14×100×20
=314×20
=6280(cm?)
答:以长为轴旋转一周,得到的圆柱的体积是6280 cm3。
练
习
五
三、巩固练习
20cm
10cm
以宽为轴旋转,得到圆柱的底面半径是20cm,高10cm。
3.14×20?×10
=3.14×400×10
=1256×10
=12560(cm?)
答:以宽为轴旋转一周,得到的圆柱的体积是12560 cm3。
练
习
五
14、右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?
三、巩固练习
15、下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
图1
图2
图3
图4
18
12
9
6
2
3
4
6
观察
对比
上面4个长方形,从左到右,长不断变短,宽不断增长;长和宽的差也不断减小。
练
习
五
三、巩固练习
15、下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
图1
图2
图3
图4
18
12
9
6
2
3
4
6
图1的体积最大。
以长方形的长为底面周长。
图1:π×(18÷π÷2)2×2= (dm3)
图2:π×(12÷π÷2)2×3= (dm3)
图3:π×(9÷π÷2)2×4= (dm3)
图4:π×(6÷π÷2)2×6= (dm3)
> > >
练
习
五
三、巩固练习
15、下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
图1
图2
图3
图4
18
12
9
6
2
3
4
6
图4的体积最大。
以长方形的宽为底面周长。
图1:π×(2÷π÷2)2×18= (dm3)
图2:π×(3÷π÷2)2×12= (dm3)
图3:π×(4÷π÷2)2×9= (dm3)
图4:π×(6÷π÷2)2×6= (dm3)
> > >
练
习
五
用长方形卷成圆柱,以宽为圆柱的高卷成的圆柱体积最大。
1
圆柱的侧面积一定时,作为圆柱底面周长的边越长,体积越大。
2
15、下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
图1
图4
18
12
9
6
2
3
4
6
三、巩固练习
练
习
五
图2
图3
四、课堂小结
通过本节课的学习,你有什么收获?
作业:
五、作业布置
