人教版八年级数学下册课件:17.1 勾股定理(15张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:17.1 勾股定理(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览




文档简介
17.1.2
利用勾股定理解决平面几何问题
人教版第十七章
复习回顾
1.请叙述勾股定理的内容.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
如果在Rt△ ABC中,∠C=90°,
那么
a
b
c
A
B
C
2.直角三角形中特殊角的性质:
直角三角形中,30 °角所对的直角边等于斜边的一半。
如果在Rt△ ABC中,∠C=90°,∠A=30°
那么
4
8
45°
8
30°
2
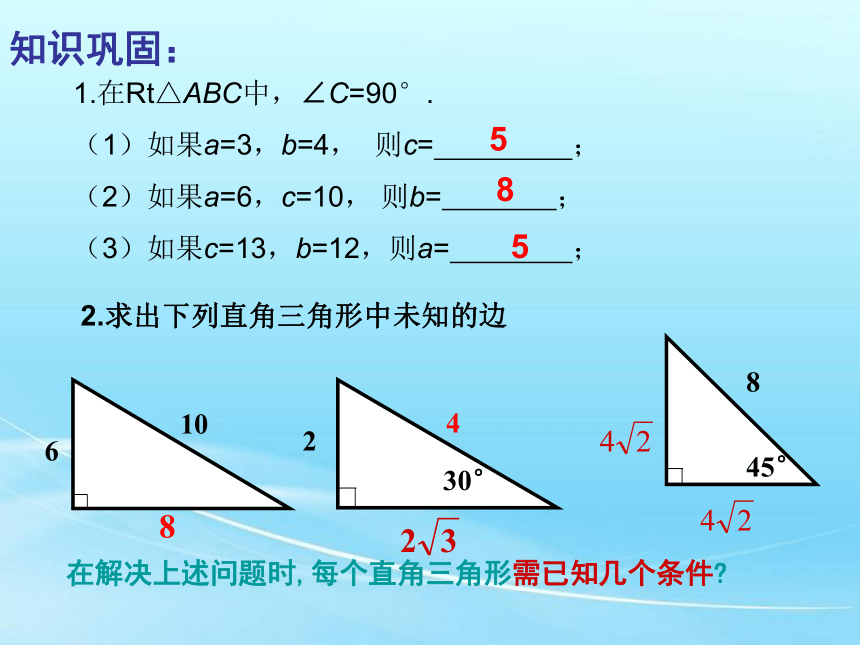
知识巩固:
在解决上述问题时,每个直角三角形需已知几个条件?
6
10
1.在Rt△ABC中,∠C=90°.
(1)如果a=3,b=4, 则c= ;
(2)如果a=6,c=10, 则b= ;
(3)如果c=13,b=12,则a= ;
2.求出下列直角三角形中未知的边
8
5
5
1、探究一:已知:在Rt△ABC中,∠C=90°,CD⊥AB于D,∠A=60°,AD= 2 ,求线段BC的长
解决问题:
变式训练:
已知:如图,△ABC中,BC=4,∠A=45°,∠B=60°,
求AB.
D
注意: 无直角三角形,作高线可得两个直角三角形,用特殊角30°和 45°的边的关系,结合勾股定理进行解题。
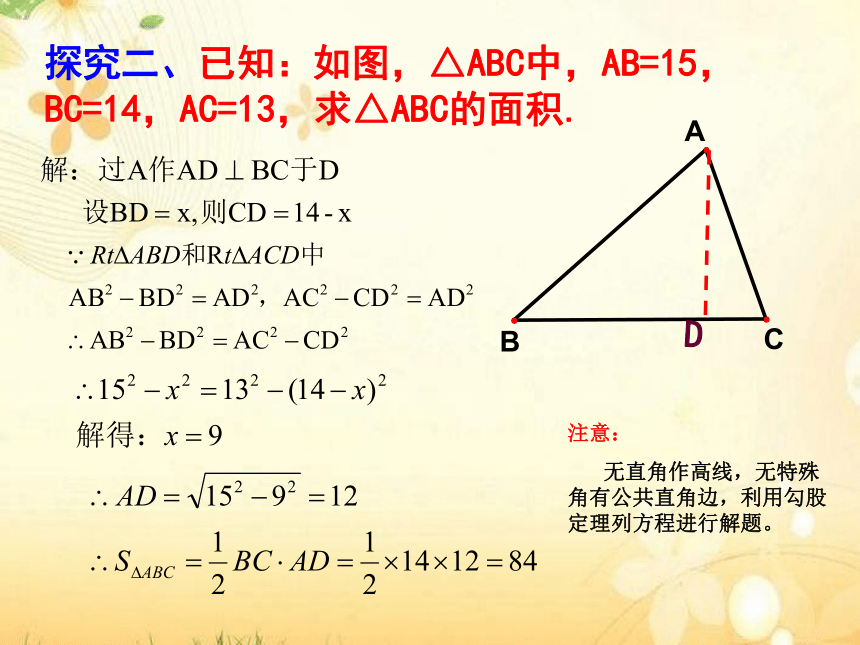
探究二、已知:如图,△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
D
注意:
无直角作高线,无特殊角有公共直角边,利用勾股定理列方程进行解题。
探究三:已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求四边形ABCD的面积.
E
注意:连接AC,也可分成两直角三角形,但用不上60°,所以考虑延长线段构造直角三角形。
探究四:已知如图,将长方形的一边BC沿CE
折叠,使得点B落在AD边的点F处,已知AB=8,BC=10, 求BE的长.
解:设BE=x,
由折叠性质得,△BCE ≌△FCE,
∴BC=FC=10,FE=BE=x,
∵四边形ABCD是长方形
∴ AB=DC=8 ,AD=BC=10,∠D=90°,
∴DF=6, AF=4,∠A=90°, AE=8-x ,
∴ ,解得 x = 5 .
∴BE 的长为5.
小结:勾股定理:
2、勾股定理的应用题型:
①已知两边求第三边;
②已知一边和一锐角(30°、60°、45°的特殊角),求其余边长;
③已知一边和另外两边的数量关系,列方程.
④结合翻折性质,转化线段之间关系,在直角三角形中利用勾股定理列方程。
1、如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2
课后训练:
1、在Rt△ABC,∠C=90°,
⑴如果a=7,c=25,则b= 。
⑵如果∠A=30°,a=4,则b= 。
⑶如果∠A=45°,a=3,则c= 。
2.已知:如图,在△ABC中,∠C=60°,AB= ,AC=4,AD是BC边上的高,求BC的长。
3.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,AB⊥AC,∠B=60°,CD=1cm,
求BC的长。
8
F
E
D
C
B
A
10
4.如下图,折叠长方形(四个角都是直角,
对边相等)的一边AD,点D落在BC边的点F处,
已知AD=8cm,DC=10cm,求EC的长.
宇宙之大,粒子之微,火箭之速,
化工之巧,地球之变,生物之谜,
日用之繁,无处不用数学。?
—— 华罗庚
利用勾股定理解决平面几何问题
人教版第十七章
复习回顾
1.请叙述勾股定理的内容.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
如果在Rt△ ABC中,∠C=90°,
那么
a
b
c
A
B
C
2.直角三角形中特殊角的性质:
直角三角形中,30 °角所对的直角边等于斜边的一半。
如果在Rt△ ABC中,∠C=90°,∠A=30°
那么
4
8
45°
8
30°
2
知识巩固:
在解决上述问题时,每个直角三角形需已知几个条件?
6
10
1.在Rt△ABC中,∠C=90°.
(1)如果a=3,b=4, 则c= ;
(2)如果a=6,c=10, 则b= ;
(3)如果c=13,b=12,则a= ;
2.求出下列直角三角形中未知的边
8
5
5
1、探究一:已知:在Rt△ABC中,∠C=90°,CD⊥AB于D,∠A=60°,AD= 2 ,求线段BC的长
解决问题:
变式训练:
已知:如图,△ABC中,BC=4,∠A=45°,∠B=60°,
求AB.
D
注意: 无直角三角形,作高线可得两个直角三角形,用特殊角30°和 45°的边的关系,结合勾股定理进行解题。
探究二、已知:如图,△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
D
注意:
无直角作高线,无特殊角有公共直角边,利用勾股定理列方程进行解题。
探究三:已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求四边形ABCD的面积.
E
注意:连接AC,也可分成两直角三角形,但用不上60°,所以考虑延长线段构造直角三角形。
探究四:已知如图,将长方形的一边BC沿CE
折叠,使得点B落在AD边的点F处,已知AB=8,BC=10, 求BE的长.
解:设BE=x,
由折叠性质得,△BCE ≌△FCE,
∴BC=FC=10,FE=BE=x,
∵四边形ABCD是长方形
∴ AB=DC=8 ,AD=BC=10,∠D=90°,
∴DF=6, AF=4,∠A=90°, AE=8-x ,
∴ ,解得 x = 5 .
∴BE 的长为5.
小结:勾股定理:
2、勾股定理的应用题型:
①已知两边求第三边;
②已知一边和一锐角(30°、60°、45°的特殊角),求其余边长;
③已知一边和另外两边的数量关系,列方程.
④结合翻折性质,转化线段之间关系,在直角三角形中利用勾股定理列方程。
1、如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2
课后训练:
1、在Rt△ABC,∠C=90°,
⑴如果a=7,c=25,则b= 。
⑵如果∠A=30°,a=4,则b= 。
⑶如果∠A=45°,a=3,则c= 。
2.已知:如图,在△ABC中,∠C=60°,AB= ,AC=4,AD是BC边上的高,求BC的长。
3.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,AB⊥AC,∠B=60°,CD=1cm,
求BC的长。
8
F
E
D
C
B
A
10
4.如下图,折叠长方形(四个角都是直角,
对边相等)的一边AD,点D落在BC边的点F处,
已知AD=8cm,DC=10cm,求EC的长.
宇宙之大,粒子之微,火箭之速,
化工之巧,地球之变,生物之谜,
日用之繁,无处不用数学。?
—— 华罗庚
