八年级数学下册课件-18.1.2 平行四边形的判定44-人教版(共19张ppt)
文档属性
| 名称 | 八年级数学下册课件-18.1.2 平行四边形的判定44-人教版(共19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览



文档简介
§18.1.2
平行四边形的判定(3)
-----三角形的中位线及定理
第十八章
平行四边形
§18.1
平行四边形
复
习
1、平行四边形的定义?
边
2、平行四边形的性质定理?
角
对角线
3、平行线间的距离?
边
4、平行四边形的判定定理?
角
对角线
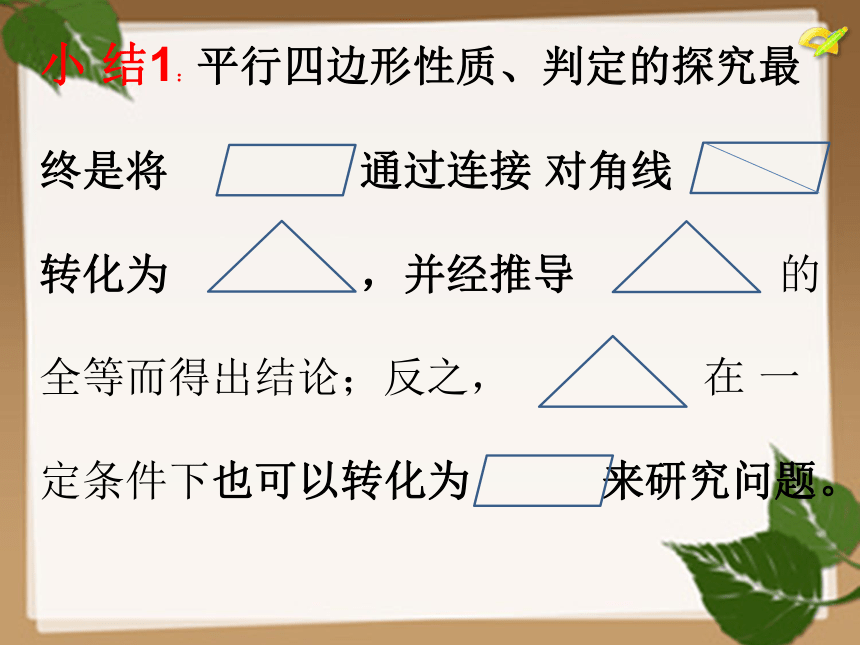
小
结1:平行四边形性质、判定的探究最
终是将
通过连接
对角线
转化为
,并经推导
的
全等而得出结论;反之,
在
一
定条件下也可以转化为
来研究问题。
如图,直线L1
∥L2,
在L1
,L2上分别截取AD,BC,使AD=BC,连接AB,CD。AB和CD有什么关系?为什么?
L1
L2
A
B
C
D
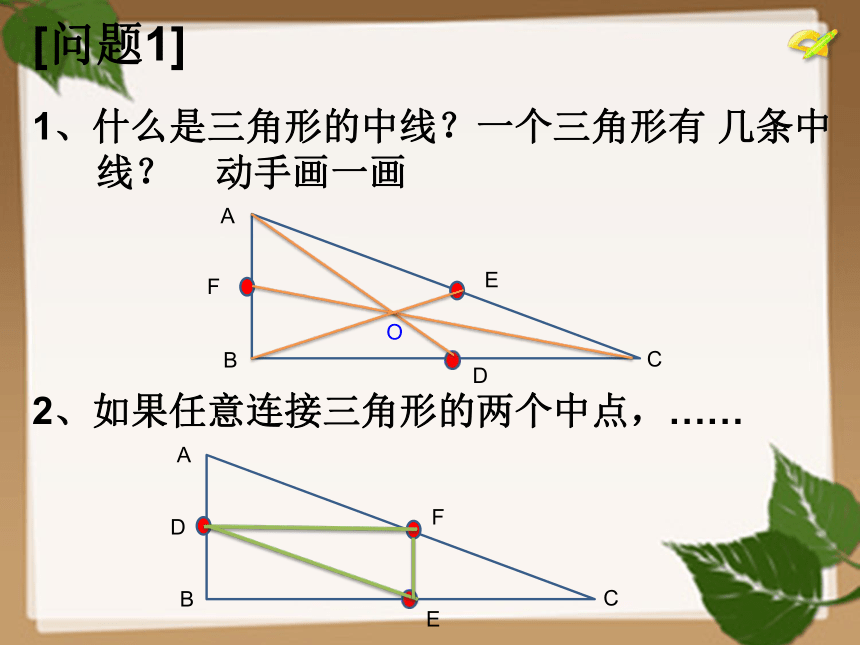
[问题1]
1、什么是三角形的中线?一个三角形有
几条中
线?
动手画一画
2、如果任意连接三角形的两个中点,……
D
F
E
A
B
C
A
B
C
F
D
E
O
D
E
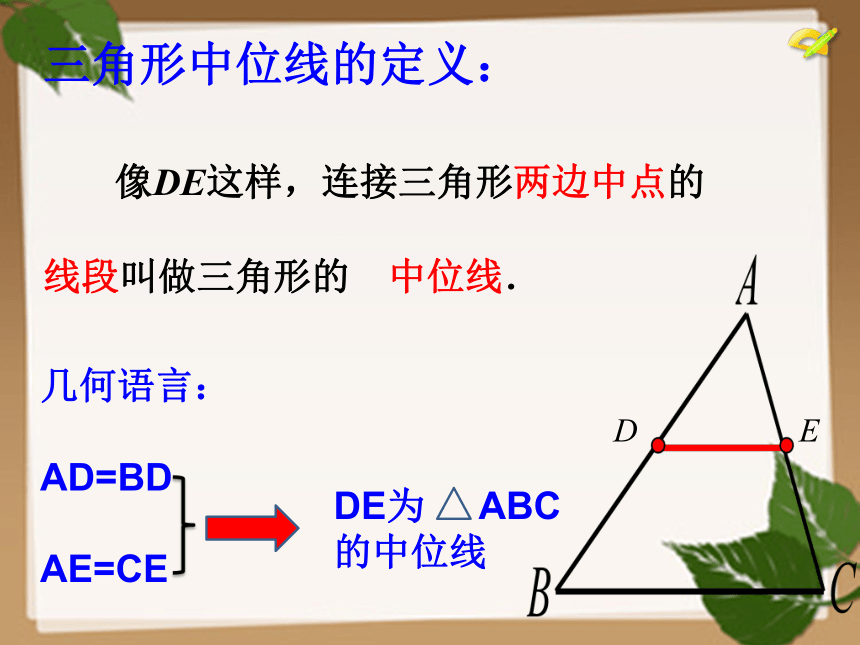
三角形中位线的定义:
像DE这样,连接三角形两边中点的
线段叫做三角形的
中位线.
几何语言:
AD=BD
AE=CE
DE为
ABC的中位线
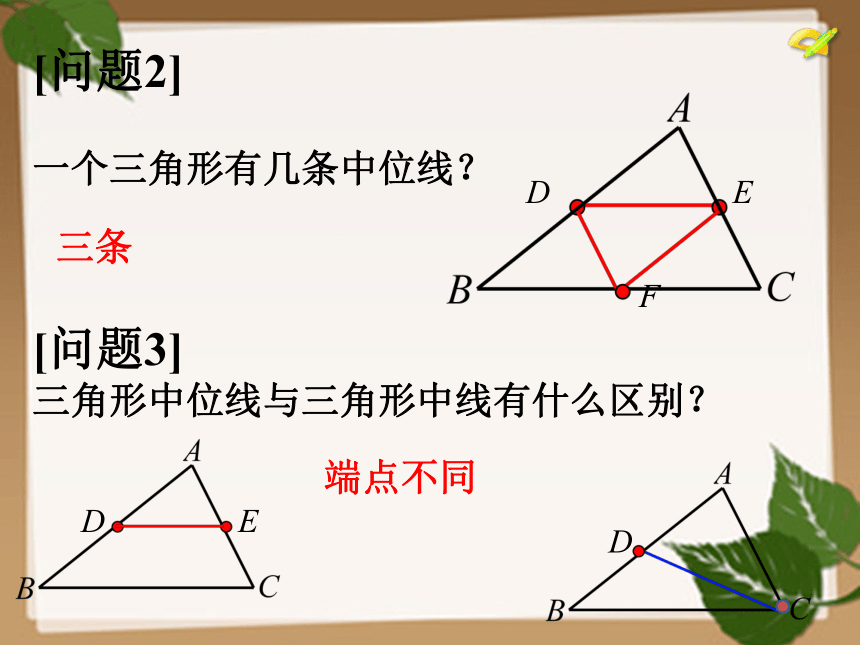
[问题2]
一个三角形有几条中位线?
三条
[问题3]
三角形中位线与三角形中线有什么区别?
D
E
端点不同
D
E
F
D
探
究:
1、给你一个三角形,你会剪成四个全等的三角形吗?剪一剪,拼一下看看!为什么?
2、在1、的基础上,你会把一个三角形剪一个角,拼成
吗?怎么剪?动手试试!
B
C
E
D
提示:通过探究1、2你发现中位线与第三边有什么特殊性了吗?
3、如图,DE是△ABC的中位线DE与BC有
怎样的关系?
两条线段的关系
位置关系
数量关系
一、观察、分析:
DE与BC的关系
二、猜想:
DE∥BC
?
D
E
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
三、度量:
猜想:
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
如何证明你的猜想?
四、证明:
已知:如图,D、E分别是△ABC的边AB、
AC的中点.
求证:DE∥BC
,
.
D
E
F
证法1:将
△
转化为
(老师展示过程)
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
∵
DE是△ABC
中位线,
三角形中位线定理:
几何语言:
∴
DE∥BC,DE=
BC.
D
E
证明:如图所示
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F
连接FC.
∵∠AED=∠CEF,AE=CE,
(下面证明同证法1)
证法2:
借助
△≌△
,AD
CF.
∴BD
CF.
又∵
D
、E分别为AB、AC的中点
证法3:数学变换(旋转、平移),证明过程为今天作业
如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么?
N
M
书上
p49
练习
3
提示:你想到了几种方法?哪种最简单?
1.
如图,△ABC中,D、E分别是AB、AC中点.
(1)
若DE=5,则BC=
.
(2)
若∠B=65°,则∠ADE=
°.
(3)
若DE+BC=12,则BC=
.
10
65
x
2x
x+2x=12
x=4
8
练习2:
2.
若三角形的周长为56cm,则它的三条中
位线组成的三角形的周长是
(
)cm.
3.
已知:如图,△ABC中,BD平分∠ABC,且D为AC的中点,DE∥BC交AB于点E,若EB=4,则线段BC的长为_____.
28
8
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
四边形问题
连接对角线
三角形问题
(三角形中位线定理)
思
考:
归纳:连接任意的四边形的各边中点的图形为平行四边形
知识方面:三角形中位线概念;
三角形中位线定理。
思想方法方面:转化思想
小
结2:
1、动手实验(观察、分析、度量);
2、数学变换(旋转、平移等);
3、添加辅助线(借助△≌△)
。
探究与命题的关系:
一、观察、分析;二、猜想;三、度量;四、证明
1、教材
P49
复习巩固
5.
3、再顺次连接思考题中所得到的四边形
EFGH各边中点,又得到一个新的四边形,
并判断这个新四边形是否是平行四边形?
说明理由。
课后作业:
2、大练习册P32
3、4、7题
