八年级数学下册课件-18.1.2 平行四边形的判定45-人教版(共22张ppt)
文档属性
| 名称 | 八年级数学下册课件-18.1.2 平行四边形的判定45-人教版(共22张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览



文档简介
三角形的中位线
A
B
趣味导入:A、B两点被池塘隔开,如何测量A、B两点距离呢?为什么?
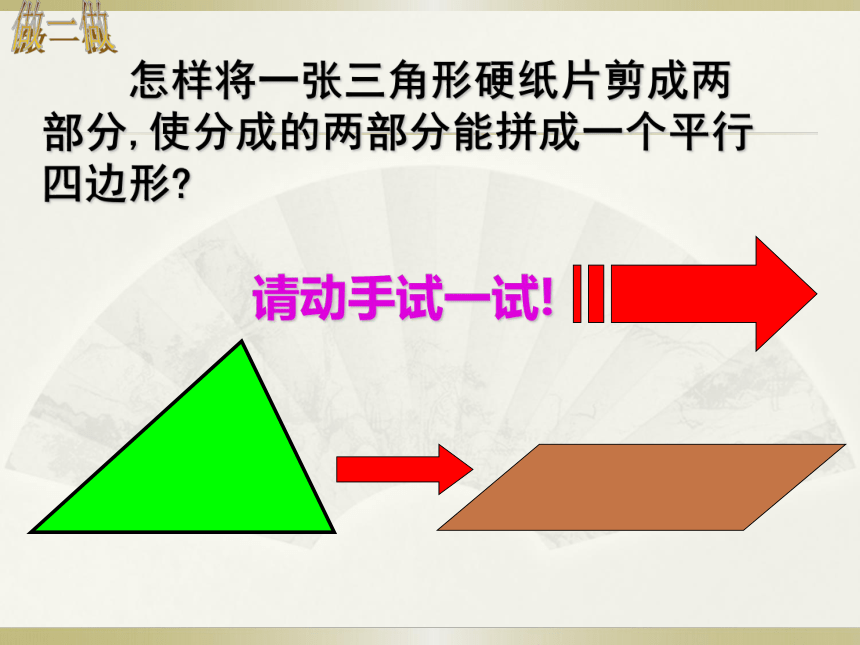
怎样将一张三角形硬纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
请动手试一试!
F
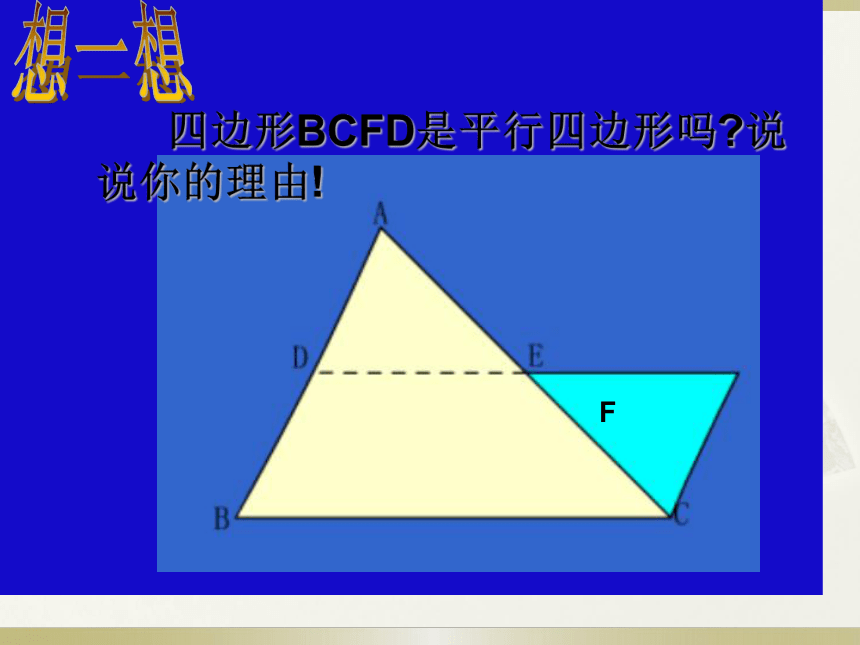
四边形BCFD是平行四边形吗?说说你的理由!
A
B
C
D
E
DE是三角形ABC的
中位线
什么叫三角形的中位线呢?
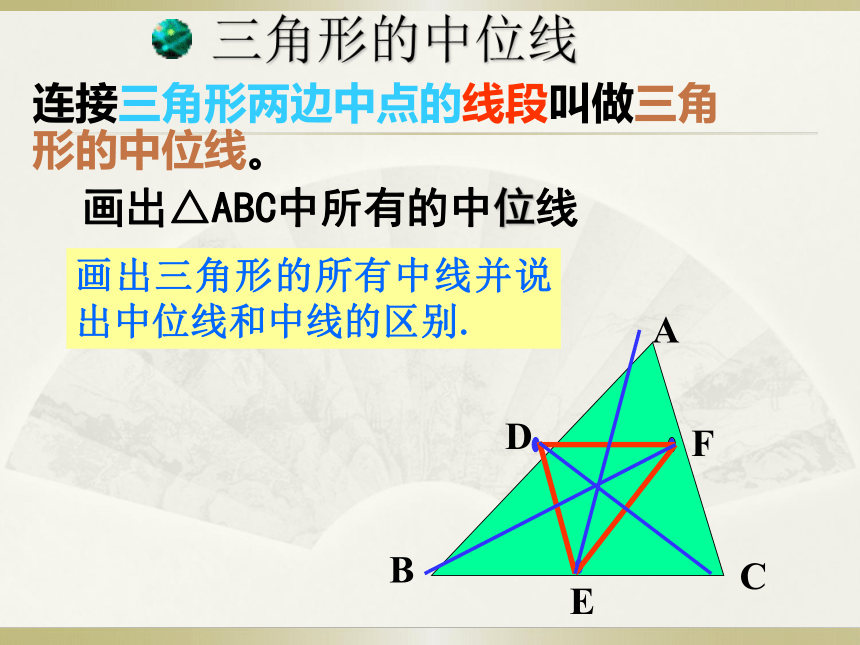
三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线。
A
B
C
画出△ABC中所有的中位线
画出三角形的所有中线并说出中位线和中线的区别.
D
E
F
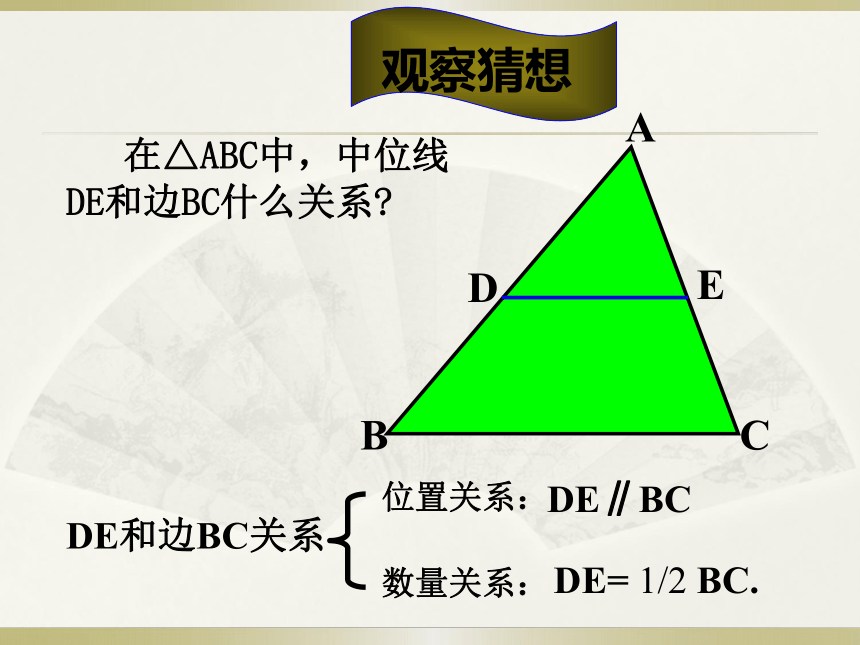
观察猜想
在△ABC中,中位线DE和边BC什么关系?
DE和边BC关系
数量关系:
位置关系:
A
B
C
D
E
DE∥BC
DE= 1/2 BC.
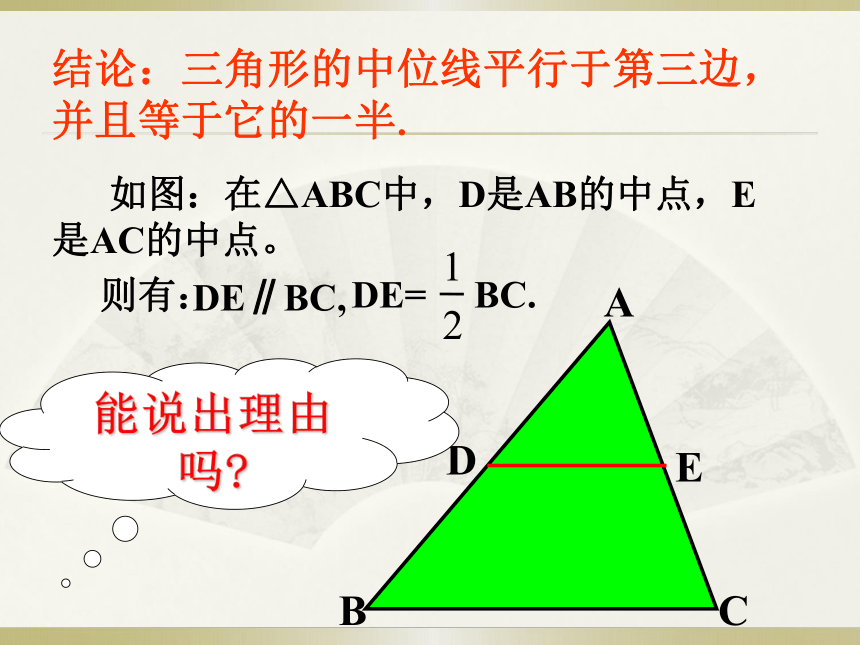
结论:三角形的中位线平行于第三边,并且等于它的一半.
E
A
B
C
D
如图:在△ABC中,D是AB的中点,E是AC的中点。
则有:
DE∥BC,
DE= BC.
2
1
能说出理由吗?
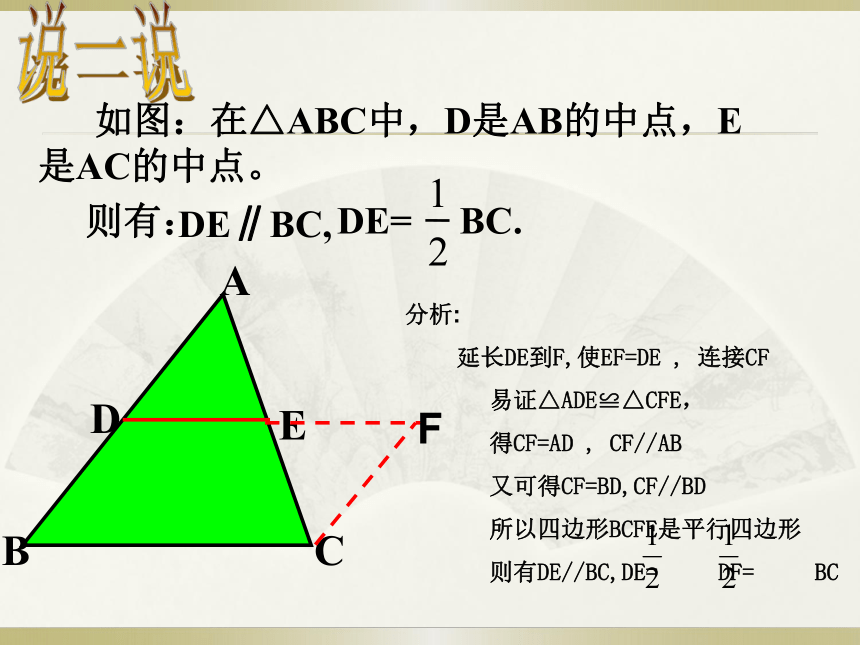
如图:在△ABC中,D是AB的中点,E是AC的中点。
则有:
DE∥BC,
DE= BC.
2
1
E
A
B
C
D
F
分析:
延长DE到F,使EF=DE , 连接CF
易证△ADE≌△CFE,
得CF=AD , CF//AB
又可得CF=BD,CF//BD
所以四边形BCFE是平行四边形
则有DE//BC,DE= DF= BC
三角形的中位线的性质
三角形的中位线平行于第三边,并且等于它的一半.
用符号语言表示
D
A
B
C
E
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
2
1
三角形各边的长分别为6 cm、8 cm 和 10 cm ,求连接各边中点所成三角形的周长.
A
B
C
D
E
F
6 cm
8 cm
10 cm
AB=10 cm
BC=8 cm
AC=6 cm
EF=5 cm
DF=4 cm
DE=3 cm
答案:12 cm
A
B
C
测出MN的长,就可知A、B两点的距离
若MN=36 m,则AB=2MN=72 m
M
N
如动画所示:在AB外选一点C,使C能直接到达A和B,
连结AC和BC,并分别找出AC和BC的中点M、N.
如图,施工队要在AB之间的湖底修一条隧道,聪明的你能帮他们不用测量就算出AB之间的距离吗?
例1、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗?为什么?
A
B
C
D
E
F
G
H
解:四边形EFGH是平行四边形.
连接AC,在△ABC中,
因为E、F分别是AB、BC边的中点,即EF是△ABC的中位线.
所以EF//AC,EF= AC
在△ADC中,同理可得
HG//AC,HG= AC
所以EF//HG,EF=HG
所以四边形EFGH是平行四边形
2
1
2
1
从例1中你能得到什么结论?
顺次连接四边形各边中点的线段组成一个平行四边形.
(1)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(3)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
(2)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
正方形
结 论
原四边形两条对角线
连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
想一想
在笔直的铁轨上, 夹在两根铁轨之间的枕木是否一样长 ?
由生活实际到数学抽象
a
b
已知直线a//b,过直线 a 上任意两点A,B 分别向直线 b 作垂线,交直线b 于点C,点D.
A
B
C
D
(1) 线段AC 、 BD所在的直线有怎样的位置关系 ?
(2) 比较线段AC 、 BD 的长短 .
两平行线间的距离
“平行线间的距离 ”
因此 , 如果两条直线平行 , 则其中一条直线上任意一点到另一条直线的距离相等 . 这个距离称为平行线之间的距离。
a
b
A
B
C
D
在例 2 中, 线段 AC 的长是点A到直线 b 的距离 ; 同样, 线段BD的长是点 B 到直线 b 的距离, 且 AC = BD.
=
“ 平行线间的垂线段的长 ”
平行线间的距离处处相等.
议 一 议
两点间的距离、点到直线的距离、两平行线间的距离有什么区别和联系?
1.三角形的中位线定义.
2.三角形的中位线定理.
3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.
4.线段的倍分要转化为相等问题来解决.
5.平行线间的距离.
小结
A
B
趣味导入:A、B两点被池塘隔开,如何测量A、B两点距离呢?为什么?
怎样将一张三角形硬纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
请动手试一试!
F
四边形BCFD是平行四边形吗?说说你的理由!
A
B
C
D
E
DE是三角形ABC的
中位线
什么叫三角形的中位线呢?
三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线。
A
B
C
画出△ABC中所有的中位线
画出三角形的所有中线并说出中位线和中线的区别.
D
E
F
观察猜想
在△ABC中,中位线DE和边BC什么关系?
DE和边BC关系
数量关系:
位置关系:
A
B
C
D
E
DE∥BC
DE= 1/2 BC.
结论:三角形的中位线平行于第三边,并且等于它的一半.
E
A
B
C
D
如图:在△ABC中,D是AB的中点,E是AC的中点。
则有:
DE∥BC,
DE= BC.
2
1
能说出理由吗?
如图:在△ABC中,D是AB的中点,E是AC的中点。
则有:
DE∥BC,
DE= BC.
2
1
E
A
B
C
D
F
分析:
延长DE到F,使EF=DE , 连接CF
易证△ADE≌△CFE,
得CF=AD , CF//AB
又可得CF=BD,CF//BD
所以四边形BCFE是平行四边形
则有DE//BC,DE= DF= BC
三角形的中位线的性质
三角形的中位线平行于第三边,并且等于它的一半.
用符号语言表示
D
A
B
C
E
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
2
1
三角形各边的长分别为6 cm、8 cm 和 10 cm ,求连接各边中点所成三角形的周长.
A
B
C
D
E
F
6 cm
8 cm
10 cm
AB=10 cm
BC=8 cm
AC=6 cm
EF=5 cm
DF=4 cm
DE=3 cm
答案:12 cm
A
B
C
测出MN的长,就可知A、B两点的距离
若MN=36 m,则AB=2MN=72 m
M
N
如动画所示:在AB外选一点C,使C能直接到达A和B,
连结AC和BC,并分别找出AC和BC的中点M、N.
如图,施工队要在AB之间的湖底修一条隧道,聪明的你能帮他们不用测量就算出AB之间的距离吗?
例1、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗?为什么?
A
B
C
D
E
F
G
H
解:四边形EFGH是平行四边形.
连接AC,在△ABC中,
因为E、F分别是AB、BC边的中点,即EF是△ABC的中位线.
所以EF//AC,EF= AC
在△ADC中,同理可得
HG//AC,HG= AC
所以EF//HG,EF=HG
所以四边形EFGH是平行四边形
2
1
2
1
从例1中你能得到什么结论?
顺次连接四边形各边中点的线段组成一个平行四边形.
(1)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(3)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
(2)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
正方形
结 论
原四边形两条对角线
连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
想一想
在笔直的铁轨上, 夹在两根铁轨之间的枕木是否一样长 ?
由生活实际到数学抽象
a
b
已知直线a//b,过直线 a 上任意两点A,B 分别向直线 b 作垂线,交直线b 于点C,点D.
A
B
C
D
(1) 线段AC 、 BD所在的直线有怎样的位置关系 ?
(2) 比较线段AC 、 BD 的长短 .
两平行线间的距离
“平行线间的距离 ”
因此 , 如果两条直线平行 , 则其中一条直线上任意一点到另一条直线的距离相等 . 这个距离称为平行线之间的距离。
a
b
A
B
C
D
在例 2 中, 线段 AC 的长是点A到直线 b 的距离 ; 同样, 线段BD的长是点 B 到直线 b 的距离, 且 AC = BD.
=
“ 平行线间的垂线段的长 ”
平行线间的距离处处相等.
议 一 议
两点间的距离、点到直线的距离、两平行线间的距离有什么区别和联系?
1.三角形的中位线定义.
2.三角形的中位线定理.
3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.
4.线段的倍分要转化为相等问题来解决.
5.平行线间的距离.
小结
