八年级数学下册课件-18.2.1 矩形9-人教版(共12张ppt)
文档属性
| 名称 | 八年级数学下册课件-18.2.1 矩形9-人教版(共12张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 134.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 10:06:47 | ||
图片预览

文档简介
18.2.1矩形的性质
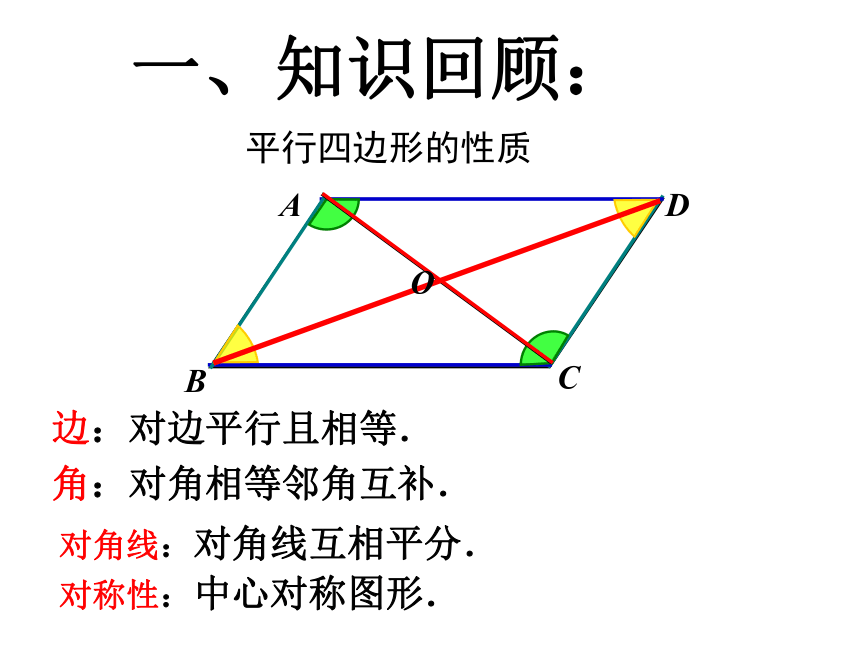
边:对边平行且相等.
角:对角相等邻角互补.
对角线:对角线互相平分.
平行四边形的性质
A
B
C
D
一、知识回顾:
O
对称性:中心对称图形.
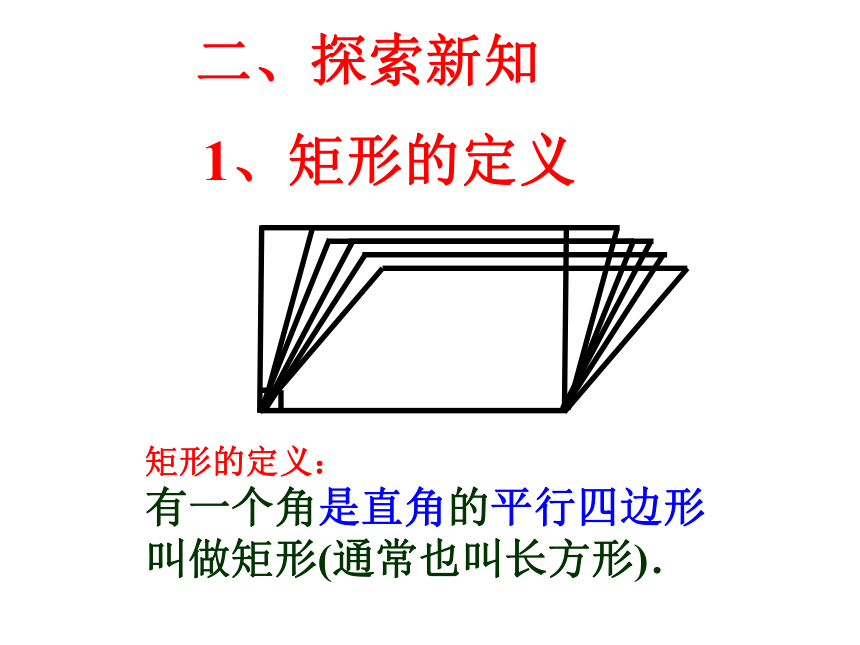
1、矩形的定义
矩形的定义:
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
二、探索新知
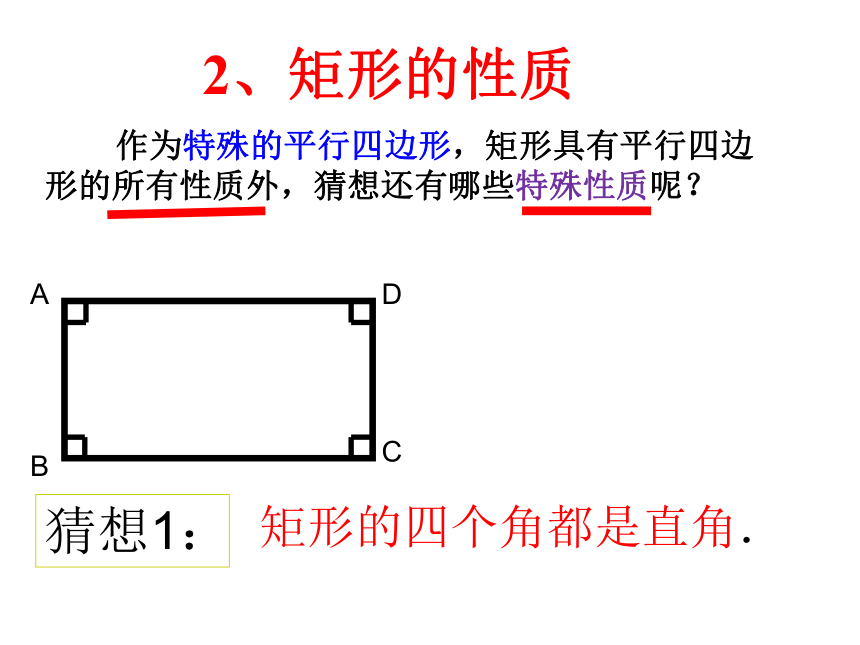
作为特殊的平行四边形,矩形具有平行四边形的所有性质外,猜想还有哪些特殊性质呢?
猜想1:
A
B
C
D
2、矩形的性质
矩形的四个角都是直角.
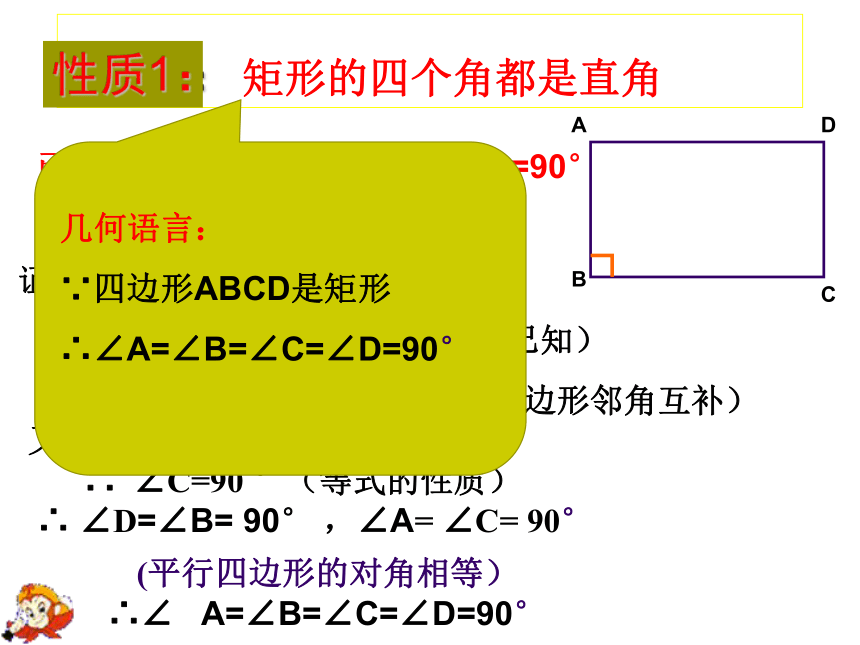
矩形的四个角都是直角
已知:四边形ABCD是矩形, ∠B=90°
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:
∵矩形ABCD是平行四边形(已知)
∴ ∠B+∠C=180 °(平行四边形邻角互补)
又 ∵ ∠B=90° (已知)
∴ ∠C=90 °(等式的性质)
∴ ∠D=∠B= 90° ,∠A= ∠C= 90°
命题1:
性质1:
几何语言:
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
(平行四边形的对角相等)
∴∠ A=∠B=∠C=∠D=90°
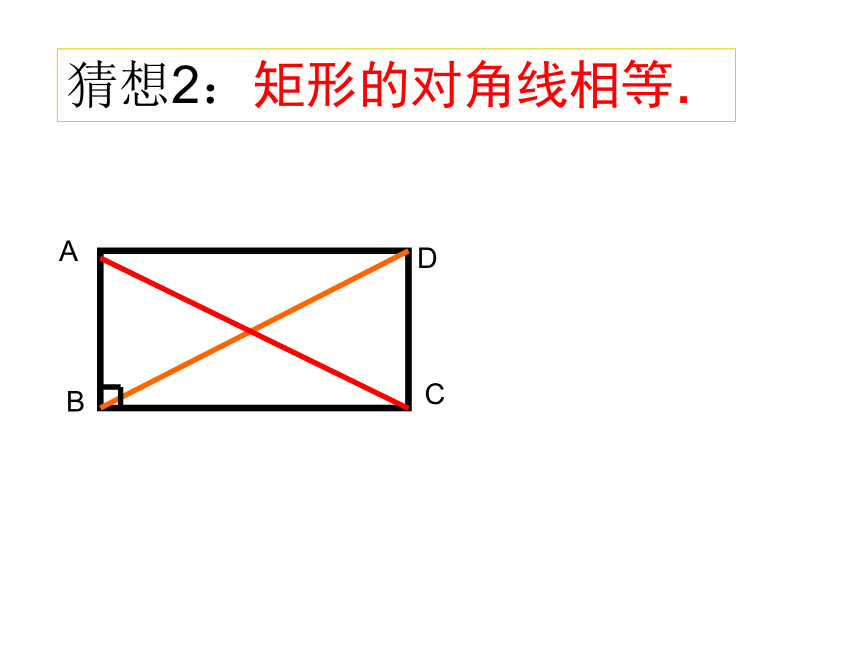
猜想2:矩形的对角线相等.
A
B
C
D
已知:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
证明: ∵ABCD是矩形(已知)
∴∠ABC = ∠DAB = 90°
BC = AD(矩形的性质)
∴△ABC≌△BAD(SAS)
∴AC = BD(对应边相等)
2:矩形的对角线相等.
命题
在△ABC和△BAD中
AB = BA
∠ABC = ∠DAB = 90°
BC = AD
{
几何语言:
∵四边形ABCD是矩形
∴ AC=BD
性质2:
例1 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
A
D
C
B
解:∵四边形ABCD是矩形
∴AC=BD,AO= AC,
BO= BD
∴AO=BO
∵∠AOB=60°
∴△ABO是等边三角形∴AO=AB=BO=4
∴AC=BD=2×4=8cm
O
矩形的对称性:
O
中心对称图形
轴对称图形
边
角
对角线
对称性
平行四
边形
矩形
小结:
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
矩形所特有的性质
2. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是
1. 下面性质中,矩形不一定具有的是
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形
3. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于
A.30° B.45° C.60° D.120°
[ ]
[ ]
[ ]
[ ]
返回
微练习
谢谢大家的聆听,再见!
边:对边平行且相等.
角:对角相等邻角互补.
对角线:对角线互相平分.
平行四边形的性质
A
B
C
D
一、知识回顾:
O
对称性:中心对称图形.
1、矩形的定义
矩形的定义:
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
二、探索新知
作为特殊的平行四边形,矩形具有平行四边形的所有性质外,猜想还有哪些特殊性质呢?
猜想1:
A
B
C
D
2、矩形的性质
矩形的四个角都是直角.
矩形的四个角都是直角
已知:四边形ABCD是矩形, ∠B=90°
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:
∵矩形ABCD是平行四边形(已知)
∴ ∠B+∠C=180 °(平行四边形邻角互补)
又 ∵ ∠B=90° (已知)
∴ ∠C=90 °(等式的性质)
∴ ∠D=∠B= 90° ,∠A= ∠C= 90°
命题1:
性质1:
几何语言:
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
(平行四边形的对角相等)
∴∠ A=∠B=∠C=∠D=90°
猜想2:矩形的对角线相等.
A
B
C
D
已知:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
证明: ∵ABCD是矩形(已知)
∴∠ABC = ∠DAB = 90°
BC = AD(矩形的性质)
∴△ABC≌△BAD(SAS)
∴AC = BD(对应边相等)
2:矩形的对角线相等.
命题
在△ABC和△BAD中
AB = BA
∠ABC = ∠DAB = 90°
BC = AD
{
几何语言:
∵四边形ABCD是矩形
∴ AC=BD
性质2:
例1 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
A
D
C
B
解:∵四边形ABCD是矩形
∴AC=BD,AO= AC,
BO= BD
∴AO=BO
∵∠AOB=60°
∴△ABO是等边三角形∴AO=AB=BO=4
∴AC=BD=2×4=8cm
O
矩形的对称性:
O
中心对称图形
轴对称图形
边
角
对角线
对称性
平行四
边形
矩形
小结:
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
矩形所特有的性质
2. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是
1. 下面性质中,矩形不一定具有的是
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形
3. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于
A.30° B.45° C.60° D.120°
[ ]
[ ]
[ ]
[ ]
返回
微练习
谢谢大家的聆听,再见!
