八年级数学下册课件-19.1.2 函数的图象7-人教版(共13张ppt)
文档属性
| 名称 | 八年级数学下册课件-19.1.2 函数的图象7-人教版(共13张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览





文档简介
函数的图象
第二课时
Contents
目录
01
02
03
04
旧知回顾
学习目标
新知探究
随堂练习
05
课堂小结
什么是函数的图象?
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象。
1、会用描点法画出函数图象,能说出画函数图象的步骤。
2、会判断一个点是否在函数的图象上。
3、能初步通过分析图象中变量的对应关系、变化规律和变化趋势,体会数形结合的思想。
例:在下列式子中,对于x每一确定的值,y都有唯一的对应值,即y是x的函数,你能画出这些函数的图象吗?
(1)y=x+0.5
(2)
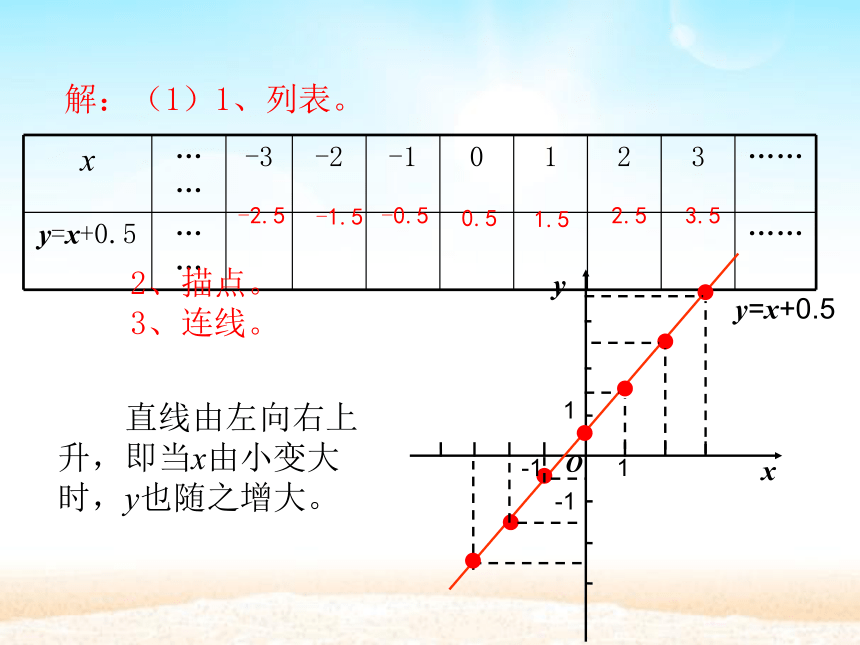
解:(1)1、列表。
x
……
-3
-2
-1
0
1
2
3
……
y=x+0.5
……
……
2、描点。
3、连线。
O
-1
1
x
y
y=x+0.5
直线由左向右上升,即当x由小变大时,y也随之增大。
-2.5
-0.5
0.5
1.5
2.5
3.5
-1.5
1
-1
解:(2)1、列表。
x
1
2
3
4
6
……
……
2、描点。
3、连线。
曲线 从左向右下降,即当x由小变大时,y随之减小。
6
3
2
1.5
1
描点法画函数图象的一般步骤。
1、列表:表中给出一些自变量的值及其对应的函数值。
2、描点:在直角坐标系中,以自变量的值为横坐标,相对应的函数值为纵坐标,描出表格中数值对应的各点。
3、连线:按照横坐标由小到大的顺序把所描出的各点用平滑的曲线连接起来。
归纳:
1、(1)画出函数y=2x-1的图象。
(2)判断A(-2.5,-4),B(1,3),C(2.5,4)是否在函数y=2x-1的图象上。
x
……
-1
0
1
……
y=2x-1
……
……
-3
-1
1
O
-1
1
x
y
1
-1
2、(1)画出函数
的图象。
(2)从图象中观察,当x<0时,y随x的增大而增大,还是y随x的增大而减小呢?当x>0时呢?
x
……
-3
-2
-1
0
1
2
3
……
……
……
9
4
1
1
0
4
9
x
y
O
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
描点,连线。
1、画函数图象的三个步骤分别是什么?
2、如何从图象中了解函数的变化情况呢?
本节课主要学习了哪些知识?
1、画出函数y=3x的图象。
2、在同一直角坐标系中画出函数y=-x与y=-x+6的图象,观察这两个图象的位置。
3、在同一直角坐标系中画出函数y=2x+6与y=-x+6的图象,观察这两个图象的位置。
作 业
谢 谢
第二课时
Contents
目录
01
02
03
04
旧知回顾
学习目标
新知探究
随堂练习
05
课堂小结
什么是函数的图象?
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象。
1、会用描点法画出函数图象,能说出画函数图象的步骤。
2、会判断一个点是否在函数的图象上。
3、能初步通过分析图象中变量的对应关系、变化规律和变化趋势,体会数形结合的思想。
例:在下列式子中,对于x每一确定的值,y都有唯一的对应值,即y是x的函数,你能画出这些函数的图象吗?
(1)y=x+0.5
(2)
解:(1)1、列表。
x
……
-3
-2
-1
0
1
2
3
……
y=x+0.5
……
……
2、描点。
3、连线。
O
-1
1
x
y
y=x+0.5
直线由左向右上升,即当x由小变大时,y也随之增大。
-2.5
-0.5
0.5
1.5
2.5
3.5
-1.5
1
-1
解:(2)1、列表。
x
1
2
3
4
6
……
……
2、描点。
3、连线。
曲线 从左向右下降,即当x由小变大时,y随之减小。
6
3
2
1.5
1
描点法画函数图象的一般步骤。
1、列表:表中给出一些自变量的值及其对应的函数值。
2、描点:在直角坐标系中,以自变量的值为横坐标,相对应的函数值为纵坐标,描出表格中数值对应的各点。
3、连线:按照横坐标由小到大的顺序把所描出的各点用平滑的曲线连接起来。
归纳:
1、(1)画出函数y=2x-1的图象。
(2)判断A(-2.5,-4),B(1,3),C(2.5,4)是否在函数y=2x-1的图象上。
x
……
-1
0
1
……
y=2x-1
……
……
-3
-1
1
O
-1
1
x
y
1
-1
2、(1)画出函数
的图象。
(2)从图象中观察,当x<0时,y随x的增大而增大,还是y随x的增大而减小呢?当x>0时呢?
x
……
-3
-2
-1
0
1
2
3
……
……
……
9
4
1
1
0
4
9
x
y
O
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
描点,连线。
1、画函数图象的三个步骤分别是什么?
2、如何从图象中了解函数的变化情况呢?
本节课主要学习了哪些知识?
1、画出函数y=3x的图象。
2、在同一直角坐标系中画出函数y=-x与y=-x+6的图象,观察这两个图象的位置。
3、在同一直角坐标系中画出函数y=2x+6与y=-x+6的图象,观察这两个图象的位置。
作 业
谢 谢
