八年级数学下册课件-19.2.1 正比例函数60-人教版(共16张ppt)
文档属性
| 名称 | 八年级数学下册课件-19.2.1 正比例函数60-人教版(共16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 830.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览





文档简介
19.2.1 正比例函数
1996年,鸟类研究者在芬兰给一只燕鸥(候鸟)套上标志环;大约128天后,人们在25600千米外的澳大利亚发现了它.
(1)这只百余克重的小鸟大约平均每天飞行多少千米?
解: 25 600÷128 = 200(km).
(2) 这只燕鸥的行程y(单位:千米)与
飞行时间x(单位:天)之间有什么关系?
解: y=200x (0≤x≤128).
(3)这只燕鸥飞行一个半月(一个月按30天计算.)的行程大约是多少千米?
解:当x=45时,y=200×45=9 000 (km).
写出下列问题中的函数关系式:
(2)铁块的质量m(单位:g)随它的体积v(单位:cm3)变化的关系(铁的密度为7.8g/cm3)
(3)每个练习本的厚度为0.5cm,一些练习本叠在一起的总厚度 h随练习本的本数n变化的关系;
(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:分)变化的关系。
(1) 圆 的 周 长 随半径 r变化的关系;
(2)m=7.8v
(3)h=0.5n
(4)T=-2t
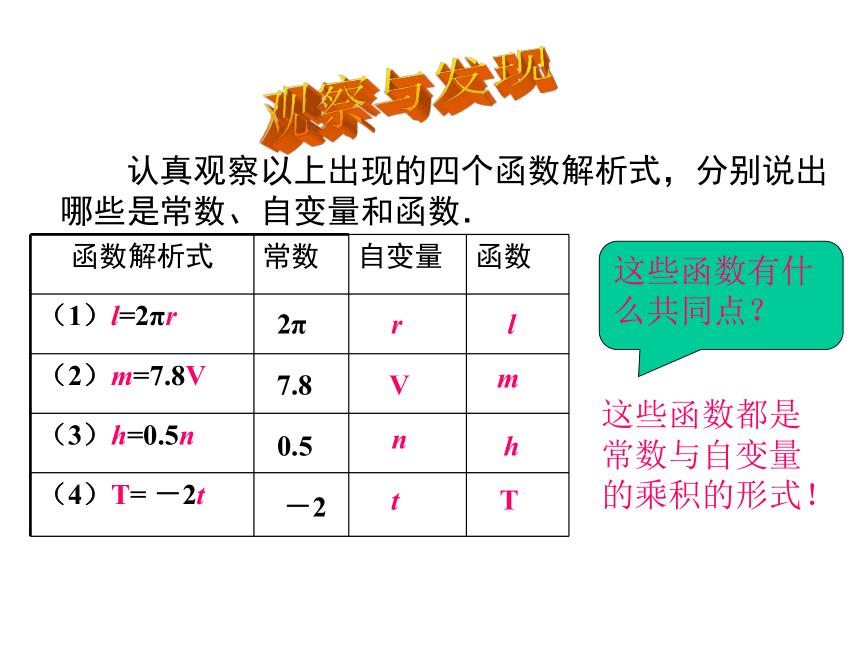
认真观察以上出现的四个函数解析式,分别说出哪些是常数、自变量和函数.
函数解析式
常数
自变量
函数
(1)l=2πr
(2)m=7.8V
(3)h=0.5n
(4)T= -2t
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式!
2π
r
l
7.8
V
m
0.5
n
h
-2
t
T
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
这里为什么强调k是常数, k≠0呢?
做一做 下列函数是否是正比例函数?比例系数是多少?
你能举出一些正比例函数的例子吗?
(4)y=2x (5)y=x2+1
(6)y=(a2+1)x-2
应用新知
练习: (1)若y=5x3m-2是正比例函数,m= 。
(2)若 是正比例函数m= 。
1
-2
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
-4
-2
0
2
4
y=2x
x
…
-2
-1
0
1
2
…
y
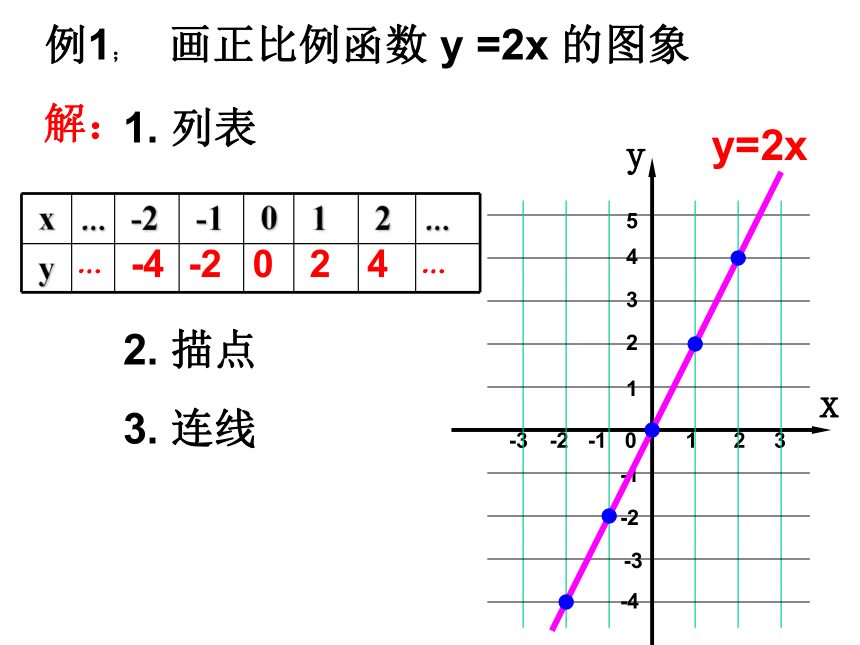
例1; 画正比例函数 y =2x 的图象
解:
1. 列表
2. 描点
3. 连线
…
…
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
1
2
3
4
5
练习:画出正比例函数y=-2x的图象?
x
y
y=2x
y=-2x
正比例函数y= kx (k≠0) 的图象是经过原点(0,0)点和(1,k)点的一条直线。
观察 比较两个函数的相同点与不同点.
归纳
两图象都是经过原点的 .函数 的图象从左向右 ,经过第 象限;函数 的图象从左向右 ,经过第 象限.
直线
上升
一、三
下降
二、四
y=x
当k>0时,图象(除原点外)在一,三象限;
当k<0时,图象(除原点外)在二,四象限;
x增大时,y的值也增大
x增大时,y的值反而减小
1
0
x
y
1
y= -x
1
0
x
y
1
1
0
x
y
1
1
0
x
y
1
x
y
x
y
性质
练一练
在同一坐标系中画出
与
的图象,并
对它们进行比较.
正比例函数y= kx (k≠0) 的图象是
x
y
0
x
y
0
1
k
当k>0时,直线y=kx 经过第一、三象限;
1
k
当k<0 时直线y=kx 经过第二、四象限。
经过原点(0,0)和点(1,k)的一条直线。
y= kx (k>0)
y= kx
(k<0)
总结新知
想一想?
经过原点与(1,k)的直线是正比例函数y=kx (k是常数, )的图象,由于两点确定一条直线,画正比例函数图象时,我们只需描点(0,0)和点 (1,k),连线即可.
经过原点与(1,k)的直线是哪个函数的图象?画正比例函数的图象时,怎样画最简单?为什么?
解:选取两点(0,0) , (1,3)
例2:画函数 y = 3x 的图象
y
y=3x
过这两点画直线,
就是函数y= 3x 的图象
-1
-3
3
2
1
-2
-3
2
3
4
5
x
-1
-2
-4
0
1
画一画
用你认为最简单的方法画出下列函数的图像
(1)
(2)
小 结
1、正比例函数的概念和性质。
2、正比例函数y=kx图像的画法:过原点与点(1,k)的直线即所求图像。
1996年,鸟类研究者在芬兰给一只燕鸥(候鸟)套上标志环;大约128天后,人们在25600千米外的澳大利亚发现了它.
(1)这只百余克重的小鸟大约平均每天飞行多少千米?
解: 25 600÷128 = 200(km).
(2) 这只燕鸥的行程y(单位:千米)与
飞行时间x(单位:天)之间有什么关系?
解: y=200x (0≤x≤128).
(3)这只燕鸥飞行一个半月(一个月按30天计算.)的行程大约是多少千米?
解:当x=45时,y=200×45=9 000 (km).
写出下列问题中的函数关系式:
(2)铁块的质量m(单位:g)随它的体积v(单位:cm3)变化的关系(铁的密度为7.8g/cm3)
(3)每个练习本的厚度为0.5cm,一些练习本叠在一起的总厚度 h随练习本的本数n变化的关系;
(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度T(单位:℃)随冷冻时间t(单位:分)变化的关系。
(1) 圆 的 周 长 随半径 r变化的关系;
(2)m=7.8v
(3)h=0.5n
(4)T=-2t
认真观察以上出现的四个函数解析式,分别说出哪些是常数、自变量和函数.
函数解析式
常数
自变量
函数
(1)l=2πr
(2)m=7.8V
(3)h=0.5n
(4)T= -2t
这些函数有什么共同点?
这些函数都是常数与自变量的乘积的形式!
2π
r
l
7.8
V
m
0.5
n
h
-2
t
T
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
这里为什么强调k是常数, k≠0呢?
做一做 下列函数是否是正比例函数?比例系数是多少?
你能举出一些正比例函数的例子吗?
(4)y=2x (5)y=x2+1
(6)y=(a2+1)x-2
应用新知
练习: (1)若y=5x3m-2是正比例函数,m= 。
(2)若 是正比例函数m= 。
1
-2
y
-4
-2
-3
-1
3
2
1
-1 0
-2
-3
1
2
3
4
5
x
-4
-2
0
2
4
y=2x
x
…
-2
-1
0
1
2
…
y
例1; 画正比例函数 y =2x 的图象
解:
1. 列表
2. 描点
3. 连线
…
…
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
1
2
3
4
5
练习:画出正比例函数y=-2x的图象?
x
y
y=2x
y=-2x
正比例函数y= kx (k≠0) 的图象是经过原点(0,0)点和(1,k)点的一条直线。
观察 比较两个函数的相同点与不同点.
归纳
两图象都是经过原点的 .函数 的图象从左向右 ,经过第 象限;函数 的图象从左向右 ,经过第 象限.
直线
上升
一、三
下降
二、四
y=x
当k>0时,图象(除原点外)在一,三象限;
当k<0时,图象(除原点外)在二,四象限;
x增大时,y的值也增大
x增大时,y的值反而减小
1
0
x
y
1
y= -x
1
0
x
y
1
1
0
x
y
1
1
0
x
y
1
x
y
x
y
性质
练一练
在同一坐标系中画出
与
的图象,并
对它们进行比较.
正比例函数y= kx (k≠0) 的图象是
x
y
0
x
y
0
1
k
当k>0时,直线y=kx 经过第一、三象限;
1
k
当k<0 时直线y=kx 经过第二、四象限。
经过原点(0,0)和点(1,k)的一条直线。
y= kx (k>0)
y= kx
(k<0)
总结新知
想一想?
经过原点与(1,k)的直线是正比例函数y=kx (k是常数, )的图象,由于两点确定一条直线,画正比例函数图象时,我们只需描点(0,0)和点 (1,k),连线即可.
经过原点与(1,k)的直线是哪个函数的图象?画正比例函数的图象时,怎样画最简单?为什么?
解:选取两点(0,0) , (1,3)
例2:画函数 y = 3x 的图象
y
y=3x
过这两点画直线,
就是函数y= 3x 的图象
-1
-3
3
2
1
-2
-3
2
3
4
5
x
-1
-2
-4
0
1
画一画
用你认为最简单的方法画出下列函数的图像
(1)
(2)
小 结
1、正比例函数的概念和性质。
2、正比例函数y=kx图像的画法:过原点与点(1,k)的直线即所求图像。
