八年级数学下册课件-19.2.2 一次函数7-人教版(共19张ppt)
文档属性
| 名称 | 八年级数学下册课件-19.2.2 一次函数7-人教版(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览





文档简介
19.2.2 一次函数 (第一课时)
人教版《义务教育教科书 · 数学》八年级下册-19章
难点名称:一次函数概念形成过程
目录
情景导学
活动研学
检测督学
反思提升
一、情境导学
一、情境导学
思考:假设故事中,瓶子为圆柱形,每个石子体积相同,瓶里原有水深 5 cm,放一粒石子水位上升 0.3 cm,那么放 x 粒石子后,水瓶的水深 y cm怎样表示呢?
y = 0.3x+5
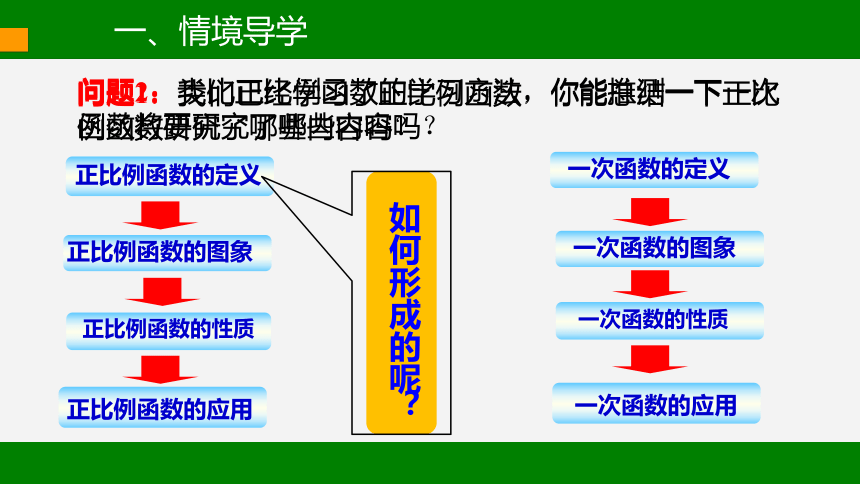
问题1:我们已经学习了正比例函数,你能总结一下正比例函数研究了哪些内容吗?
正比例函数的定义
正比例函数的图象
正比例函数的性质
正比例函数的应用
一次函数的图象
一次函数的性质
一次函数的应用
问题2:类比正比例函数的学习方法,你能推测一下一次函数将要研究了哪些内容吗?
如何形成的呢?
一次函数的定义
一、情境导学
一、情境导学
问题3:正比例函数概念是如何形成的?
实际问题
抽取出解析式
从解析式的形式特征
上定义
活动一:感悟概念
二、活动研学
问题4:类比正比例函数概念的形成过程,你认为该如何来学习一次函数的概念呢?
3.某城市的市内电话的月收费额 y (单位:元)包括月租费22元和拨打电话 x 分钟的计时费(按0.1元/分钟收取);
2.一种计算成年人标准体重G(单位:kg)的方法是:以厘米为单位量出身高值 h ,再减常数105,所得差是G 的值;
1.有人发现,在20 ℃~25 ℃时蟋蟀每分鸣叫次数 c 与温度 t(单位:℃)有关,且 c 的值约是 t 的7 倍与35的差;
问题5: 下列问题中,两变量间是函数关系式吗?若是,请写出函数关系式.
二、活动研学
(20≤ t ≤25)
4.某登山队大本营所在地的气温为5 ℃,海拔每升高1 km 气温下降6 ℃.登山队员由大本营向上登高 x km时,他们所处位置的气温是 y ℃.试用函数解析式表示 y 与 x 的关系.
y= -6x+5
问题6: 观察以上出现的五个函数解析式,类比正比例函数 y=kx(k≠0)的定义方式,你能写出一次函数的一般式吗?
二、活动研学
y = 0.3x+5
(20≤t≤25)
C = 7t - 35
y = 0.1x+22
y = -6x+5
G = h-105
活动二:形成概念
问题7: 关注一次函数的一般表达式的特征,你能提出哪些问题呢?
一般地,形如 y =kx +b (k,b为常数,k≠0)的函数,叫一次函数.
概念
精致
k、b都是常数,且k≠0.
①从次数看:
②从外形看:
自变量 x 的次数是 1
③从常数看:
解析式右边是关于自变量 x 的一次二项式.
二、活动研学
活动三:理解概念
①一次函数 y=kx+b(k≠0)中的可以为零吗?当 b= 0 时, y=kx+b(k≠0)变成了什么函数?
当 b= 0 时,y=kx+b 就变成了正比例函数 y=kx ( k≠0 ).
一次函数
正比例函数
③请在(1)(2)两个区域内填上
一次函数与正比例函数.
②一次函数与正比例函数之间有何关系?
正比例函数
问题8: 对比 y=kx+b (k≠0) 与 y=kx(k≠0) 回答下列问题.
(1)
(2)
一次函数
特殊化
都是
二、活动研学
应用1--我辨析
问题9: 下列函数中哪些是一次函数,哪些还是正比例函数?并说明理由
y 是 x 的一次函数的有 ,
y 是 x 的正比例函数的有 .(只填序号)
①②④
①
三、检测评学
应用2--我深化
问题10: 若 是一次函数,求 的值.
矛盾舍去
解:依题意得
三、检测督学
应用3--我活用<故事的延续…>
问题11:在前面乌鸦喝水的故事中,假设瓶子为圆柱形,每个石子体积相同,瓶里原有水深5cm,放一粒石子水位上升0.3cm,瓶高10cm,乌鸦嘴长2cm,投入的石子的个数为a,请分组写出下列变量关于a的关系式
①水面的高度x; ②水面上升的高度 y; ③水面与瓶口的距离Z;
活动要求:①小组合作讨论;
②1-2组写 x 与 a 的关系式,3-4组完成 y 与 a 的关系式,
5-6组写 Z 与 a 的关系式.
三、检测督学
① x = 5+0.3a
② y = 0.3a
③ Z=5-0.3a
8=5+0.3a a=10
3=0.3a a=10
2=5-0.3a a=10
问题12: 在上面的三种情况中,每种情况最少投入多少个石子,乌鸦正好可以喝到水?
追问1:借助三个函数关系式求得同体积石子的个数一样吗?
追问2: 通过一致的结果我们可以得到什么启示呢?
启示:我们用不同的两个变量解决同一问题,虽然函数解析式不同,但殊途同归,求得的结果一致,说明建立函数解析式时,所设自变量与函数可以不一样,但不影响问题解决的结果.
三、检测督学
问题11:在前面乌鸦喝水的故事中,假设瓶子为圆柱形,每个石子大小相同,瓶里原有水深5cm,放一粒石子水位上升0.3cm,瓶高10cm,乌鸦嘴长2cm,投入的石子的个数为a,请分组写出下列变量关于a的关系式
①水面的高度 x; ②水面上升的高度 y; ③水面与瓶口的距离 Z;
请以小组合作的形式,将本节课学到内容整理成知识结构图或知识树,画在草稿纸上,然后上台展示、分享。
四、反思提升
四、反思提升
函 数
正比例函数
一次函数(定义)
实际问题
解析式
定义
类比思想
研究方法
抽象
建模
2.类比正比例函数的学习过程,举出一个一次函数的实例,写出它的解析式并尝试画出这个函数的图象,试探究这个函数的性质,下节课以小组为单位展示你们研究的成果.
1.课本P90--91页练习第2、3题
五、课外延伸
感 谢 指 导!
人教版《义务教育教科书 · 数学》八年级下册-19章
难点名称:一次函数概念形成过程
目录
情景导学
活动研学
检测督学
反思提升
一、情境导学
一、情境导学
思考:假设故事中,瓶子为圆柱形,每个石子体积相同,瓶里原有水深 5 cm,放一粒石子水位上升 0.3 cm,那么放 x 粒石子后,水瓶的水深 y cm怎样表示呢?
y = 0.3x+5
问题1:我们已经学习了正比例函数,你能总结一下正比例函数研究了哪些内容吗?
正比例函数的定义
正比例函数的图象
正比例函数的性质
正比例函数的应用
一次函数的图象
一次函数的性质
一次函数的应用
问题2:类比正比例函数的学习方法,你能推测一下一次函数将要研究了哪些内容吗?
如何形成的呢?
一次函数的定义
一、情境导学
一、情境导学
问题3:正比例函数概念是如何形成的?
实际问题
抽取出解析式
从解析式的形式特征
上定义
活动一:感悟概念
二、活动研学
问题4:类比正比例函数概念的形成过程,你认为该如何来学习一次函数的概念呢?
3.某城市的市内电话的月收费额 y (单位:元)包括月租费22元和拨打电话 x 分钟的计时费(按0.1元/分钟收取);
2.一种计算成年人标准体重G(单位:kg)的方法是:以厘米为单位量出身高值 h ,再减常数105,所得差是G 的值;
1.有人发现,在20 ℃~25 ℃时蟋蟀每分鸣叫次数 c 与温度 t(单位:℃)有关,且 c 的值约是 t 的7 倍与35的差;
问题5: 下列问题中,两变量间是函数关系式吗?若是,请写出函数关系式.
二、活动研学
(20≤ t ≤25)
4.某登山队大本营所在地的气温为5 ℃,海拔每升高1 km 气温下降6 ℃.登山队员由大本营向上登高 x km时,他们所处位置的气温是 y ℃.试用函数解析式表示 y 与 x 的关系.
y= -6x+5
问题6: 观察以上出现的五个函数解析式,类比正比例函数 y=kx(k≠0)的定义方式,你能写出一次函数的一般式吗?
二、活动研学
y = 0.3x+5
(20≤t≤25)
C = 7t - 35
y = 0.1x+22
y = -6x+5
G = h-105
活动二:形成概念
问题7: 关注一次函数的一般表达式的特征,你能提出哪些问题呢?
一般地,形如 y =kx +b (k,b为常数,k≠0)的函数,叫一次函数.
概念
精致
k、b都是常数,且k≠0.
①从次数看:
②从外形看:
自变量 x 的次数是 1
③从常数看:
解析式右边是关于自变量 x 的一次二项式.
二、活动研学
活动三:理解概念
①一次函数 y=kx+b(k≠0)中的可以为零吗?当 b= 0 时, y=kx+b(k≠0)变成了什么函数?
当 b= 0 时,y=kx+b 就变成了正比例函数 y=kx ( k≠0 ).
一次函数
正比例函数
③请在(1)(2)两个区域内填上
一次函数与正比例函数.
②一次函数与正比例函数之间有何关系?
正比例函数
问题8: 对比 y=kx+b (k≠0) 与 y=kx(k≠0) 回答下列问题.
(1)
(2)
一次函数
特殊化
都是
二、活动研学
应用1--我辨析
问题9: 下列函数中哪些是一次函数,哪些还是正比例函数?并说明理由
y 是 x 的一次函数的有 ,
y 是 x 的正比例函数的有 .(只填序号)
①②④
①
三、检测评学
应用2--我深化
问题10: 若 是一次函数,求 的值.
矛盾舍去
解:依题意得
三、检测督学
应用3--我活用<故事的延续…>
问题11:在前面乌鸦喝水的故事中,假设瓶子为圆柱形,每个石子体积相同,瓶里原有水深5cm,放一粒石子水位上升0.3cm,瓶高10cm,乌鸦嘴长2cm,投入的石子的个数为a,请分组写出下列变量关于a的关系式
①水面的高度x; ②水面上升的高度 y; ③水面与瓶口的距离Z;
活动要求:①小组合作讨论;
②1-2组写 x 与 a 的关系式,3-4组完成 y 与 a 的关系式,
5-6组写 Z 与 a 的关系式.
三、检测督学
① x = 5+0.3a
② y = 0.3a
③ Z=5-0.3a
8=5+0.3a a=10
3=0.3a a=10
2=5-0.3a a=10
问题12: 在上面的三种情况中,每种情况最少投入多少个石子,乌鸦正好可以喝到水?
追问1:借助三个函数关系式求得同体积石子的个数一样吗?
追问2: 通过一致的结果我们可以得到什么启示呢?
启示:我们用不同的两个变量解决同一问题,虽然函数解析式不同,但殊途同归,求得的结果一致,说明建立函数解析式时,所设自变量与函数可以不一样,但不影响问题解决的结果.
三、检测督学
问题11:在前面乌鸦喝水的故事中,假设瓶子为圆柱形,每个石子大小相同,瓶里原有水深5cm,放一粒石子水位上升0.3cm,瓶高10cm,乌鸦嘴长2cm,投入的石子的个数为a,请分组写出下列变量关于a的关系式
①水面的高度 x; ②水面上升的高度 y; ③水面与瓶口的距离 Z;
请以小组合作的形式,将本节课学到内容整理成知识结构图或知识树,画在草稿纸上,然后上台展示、分享。
四、反思提升
四、反思提升
函 数
正比例函数
一次函数(定义)
实际问题
解析式
定义
类比思想
研究方法
抽象
建模
2.类比正比例函数的学习过程,举出一个一次函数的实例,写出它的解析式并尝试画出这个函数的图象,试探究这个函数的性质,下节课以小组为单位展示你们研究的成果.
1.课本P90--91页练习第2、3题
五、课外延伸
感 谢 指 导!
