八年级数学下册课件-19.2.3 一次函数与方程、不等式21-人教版(共23张ppt)
文档属性
| 名称 | 八年级数学下册课件-19.2.3 一次函数与方程、不等式21-人教版(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 12:03:53 | ||
图片预览





文档简介
第十九章 一次函数
19.2.3 一次函数与方程、不等式
(1)y=ax+b (a,b为常数,且a≠0)
(2)ax+b=0 (a,b为常数,且a≠0)
(3)ax+b>0 (a,b为常数,且a≠0)
课前复习
观察:这3个式子等号或不等号左右两边有什么相同点?
相同点:都含有ax+b
下面三个式子各是什么名称?
一次函数
一元一次方程
一元一次不等式
新课引入:
(快速回答:只选一个做,做完后和前后座交流,也可以两个都做)
(1)解方程2x+20=0
(2)当自变量x为何值时,函数y=2x+20的值为0?
解:(1) 2x+20=0
(2) 当y=0时 ,即
从“数”上看
两个问题实际上是同一个问题.
注:ax+b是否相同,y取的值与方程等号右边的值是否相等。
(转化为方程)
序号
一元一次方程问题
一次函数问题
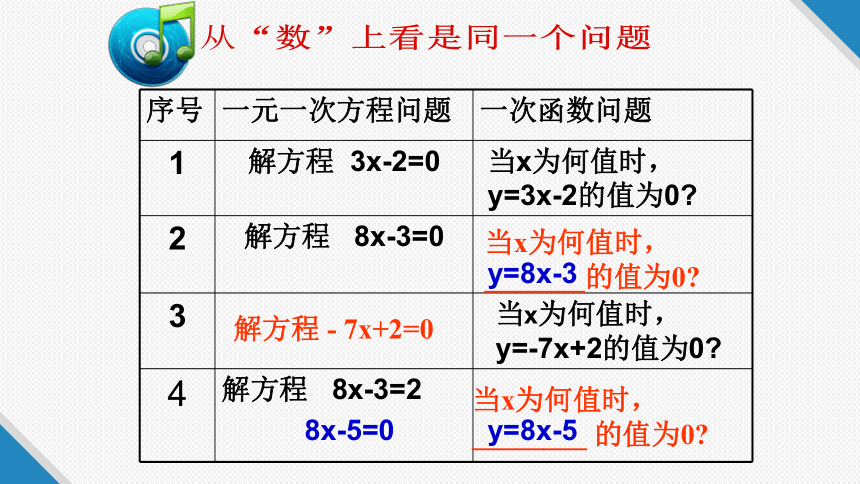
1
解方程 3x-2=0
当x为何值时,
y=3x-2的值为0?
2
解方程 8x-3=0
3
当x为何值时,
y=-7x+2的值为0?
4
解方程 8x-3=2
从“数”上看是同一个问题
当x为何值时,_______的值为0?
解方程 - 7x+2=0
8x-5=0
y=8x-3
当x为何值时,________ 的值为0?
y=8x-5
研读课文
认真阅读课本第96页的内容,完成
下面练习并体验知识点的形成过程.
1、观察下面3个方程有什么相同点与不同点?
(1)
(2)
(3)
以上3个方程相同的特点是:等号左边都是 ,不同点是:等号右边分别是 , , .
0
3
-1
2、从函数的角度对这3个方程进行解释.
(1)2x+1=3 (2)2x+1=0 (3)2x+1=-1
从“数”上:3个方程相当于在一次函数 的函数值分别为3,0,-1时,求自变 量的值.
研读课文
(求自变量x的值)
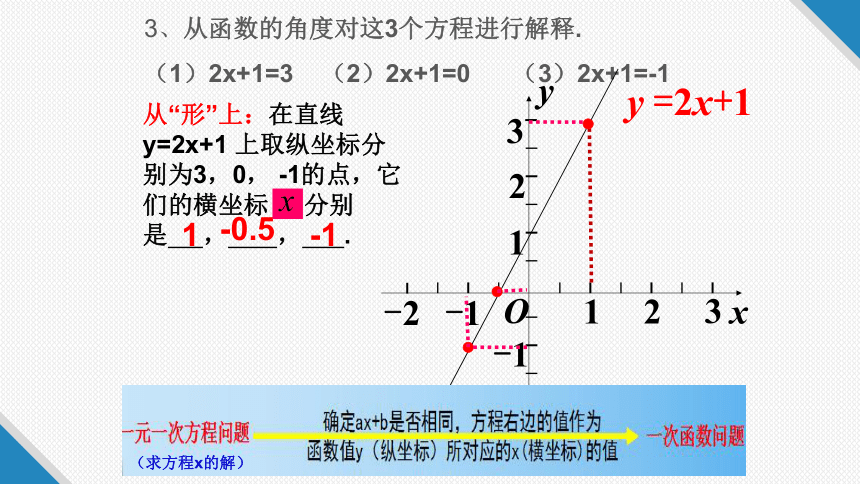
3、从函数的角度对这3个方程进行解释.
(1)2x+1=3 (2)2x+1=0 (3)2x+1=-1
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =2x+1
从“形”上:在直线y=2x+1 上取纵坐标分别为3,0, -1的点,它们的横坐标 分别是 , , .
1
-0.5
-1
(求方程x的解)
练一练:
1、方程2x+6=0的解为x=-3 ,当x= 时,函数y=2x+6的值为0。
-3
2、方程 3x+2=8 的解是 ,则函数 y=3x+2 在自变量 x 等于 时的函数值是8.
χ=2
2
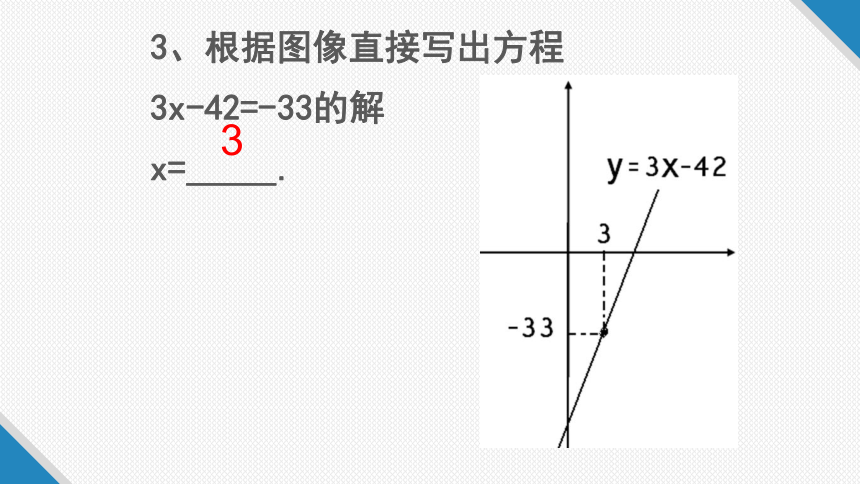
3、根据图像直接写出方程
3x-42=-33的解
x=_____.
3
4、直线y=ax+b在坐标系中的位置如
图,则方程 ax+b=0的解是χ=___
-2
2
x
y
0
-2
练一练:
新课引入:(类比)
(快速回答:只选一个做,做完后和前后座交流,也可以两个都做)
(1)解不等式3x+2>0
(2)当自变量x取何值时,函数y=3x+2的值大于0?
解:(1) 3x+2>0
(2) 当y>0时 ,即
从“数”上看
两个问题实际上是同一个问题.
注:ax+b是否相同,y的取值范围与不等式是否一致。
3x>-2
x>
3x+2>0
3x>-2
x>
(转化为不等式)
序号
一元一次不等式问题
一次函数问题
1
解不等式 3x-2<0
当x取何值时,
y=3x-2的值小于0?
2
解不等式 3x-2<-1
3
当x取何值时,
y=-7x+2的值大于0?
从“数”上
当x取何值时,_______的值小于-1?
解不等式 - 7x+2>0
y=3x-2
研读课文
1、观察下面3个不等式有什么相同点与
不同点?
(1)
>2;
(2)
<0;
(3)
<-1
3个不等式相同的特点是:不等号左边都
是 ;不同点是:不等号及不等号右
边分别是 , , .
2
0
-1
3x+2
认真阅读课本第96至97页的内容,完成下面练习并体验知识点的形成过程.
研读课文
2、你能从函数的角度对这3个不等式进行解释吗?(1)3x+2>2 (2)3x+2<0 (3)3x+2<-1
的取值范围.
的函数值分别为 、
、 时,求
自变量
从“数”上:这3个不等式相当
于在一次函数
小于-1
大于2
小于0
3x+2>2
3x+2<0
3x+2
(求自变量x的取值范围)
研读课文
从“形”上:在直线
上取纵坐标分别
满足条件 、 、 的点,看他
们的横坐标分别满足什么条件
大于2
小于0
小于-1
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
(求x的取值范围)
(1)3x+2>2
(2)3x+2<0
(3)3x+2<-1
练一练
<0.
时,
当
1、已知函数
,当
时,
>0;
> 3
< 3
2、已知一次函数
的图象如图所
>0的解集是( )
示,则不等式
A.x>-2? B.x<-2
C.x>-1???? D.x<-1
B
轴上方时
上的点在
3、直线
A.x>1?? B.x≥1 C.x<1?? D.x≤1
对应的自变量的范围是( ? )
4、已知直线
(-2,0),
则关于不等式
<0
集是 (? )
的解
A.x>-2? ??B.x≥-2
C.x<-2???? D.x≤-2
轴的交点为
与
C
A
归纳总结
一次函数问题
y取一个常数值
一元一次方程问题
一元一次方程问题
确定ax+b是否相同,方程右边的值作为
函数值y(纵坐标)所对应的x(横坐标)的值
一次函数问题
一次函数问题
一元一次不等式问题
y取一个范围
一元一次不等式问题
一次函数问题
确定ax+b是否相同,不等式(“>”或“<”)右边的值作为函数值y(纵坐标)所对应的x(横坐标)的取值范围
(求自变量x的值)
(求方程x的解)
(求自变量x的取值范围)
(求x的取值范围)
一次函数问题
一元一次不等式问题
y取一个范围
一元一次不等式问题
一次函数问题
(求自变量x的取值范围)
(求x的取值范围)
巩固训练
的值大于0?
1、当自变量
为何值时,函数
分析:“函数
的值大于0”就是y大于0,
即,
解:据题意得
所以,当自变量
时,函数
的值大于0。
2、直线 与 轴的交点是(? )
A.(0,-3)???B.(-3,0)????
C.(0,3)??? D.(0,-3)
B
轴下方?
的值满足_______时,直线
3、当自变量
上的点在
x<2
4、试根据函数
的性质或图象,
确定
取何值时:
(1)
>0;
<0
(2)
分析:根据函数图象在x轴下方的部分,y<0,
与x轴的交点y=0,在x轴上方的部分,y>0
解:令 ,解得,
∵函数 中k=3>0,
∴y随x的增大而增大,
∴(1)当x>5时,y>0;
(2)当x<5时,y<0.
5、根据图象,你能直接说出一元一次方程 的解吗?
解:由图象可知χ+3=0的
解为χ= ?3.
3
x
y
0
-3
从“形”上看
直线y=x+3的图象与x轴交点坐标为 (_-3_,_0_ ),这说明方程χ+3=0的解是x=_-3_)
Thank you!
谢谢同学们的努力!
19.2.3 一次函数与方程、不等式
(1)y=ax+b (a,b为常数,且a≠0)
(2)ax+b=0 (a,b为常数,且a≠0)
(3)ax+b>0 (a,b为常数,且a≠0)
课前复习
观察:这3个式子等号或不等号左右两边有什么相同点?
相同点:都含有ax+b
下面三个式子各是什么名称?
一次函数
一元一次方程
一元一次不等式
新课引入:
(快速回答:只选一个做,做完后和前后座交流,也可以两个都做)
(1)解方程2x+20=0
(2)当自变量x为何值时,函数y=2x+20的值为0?
解:(1) 2x+20=0
(2) 当y=0时 ,即
从“数”上看
两个问题实际上是同一个问题.
注:ax+b是否相同,y取的值与方程等号右边的值是否相等。
(转化为方程)
序号
一元一次方程问题
一次函数问题
1
解方程 3x-2=0
当x为何值时,
y=3x-2的值为0?
2
解方程 8x-3=0
3
当x为何值时,
y=-7x+2的值为0?
4
解方程 8x-3=2
从“数”上看是同一个问题
当x为何值时,_______的值为0?
解方程 - 7x+2=0
8x-5=0
y=8x-3
当x为何值时,________ 的值为0?
y=8x-5
研读课文
认真阅读课本第96页的内容,完成
下面练习并体验知识点的形成过程.
1、观察下面3个方程有什么相同点与不同点?
(1)
(2)
(3)
以上3个方程相同的特点是:等号左边都是 ,不同点是:等号右边分别是 , , .
0
3
-1
2、从函数的角度对这3个方程进行解释.
(1)2x+1=3 (2)2x+1=0 (3)2x+1=-1
从“数”上:3个方程相当于在一次函数 的函数值分别为3,0,-1时,求自变 量的值.
研读课文
(求自变量x的值)
3、从函数的角度对这3个方程进行解释.
(1)2x+1=3 (2)2x+1=0 (3)2x+1=-1
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =2x+1
从“形”上:在直线y=2x+1 上取纵坐标分别为3,0, -1的点,它们的横坐标 分别是 , , .
1
-0.5
-1
(求方程x的解)
练一练:
1、方程2x+6=0的解为x=-3 ,当x= 时,函数y=2x+6的值为0。
-3
2、方程 3x+2=8 的解是 ,则函数 y=3x+2 在自变量 x 等于 时的函数值是8.
χ=2
2
3、根据图像直接写出方程
3x-42=-33的解
x=_____.
3
4、直线y=ax+b在坐标系中的位置如
图,则方程 ax+b=0的解是χ=___
-2
2
x
y
0
-2
练一练:
新课引入:(类比)
(快速回答:只选一个做,做完后和前后座交流,也可以两个都做)
(1)解不等式3x+2>0
(2)当自变量x取何值时,函数y=3x+2的值大于0?
解:(1) 3x+2>0
(2) 当y>0时 ,即
从“数”上看
两个问题实际上是同一个问题.
注:ax+b是否相同,y的取值范围与不等式是否一致。
3x>-2
x>
3x+2>0
3x>-2
x>
(转化为不等式)
序号
一元一次不等式问题
一次函数问题
1
解不等式 3x-2<0
当x取何值时,
y=3x-2的值小于0?
2
解不等式 3x-2<-1
3
当x取何值时,
y=-7x+2的值大于0?
从“数”上
当x取何值时,_______的值小于-1?
解不等式 - 7x+2>0
y=3x-2
研读课文
1、观察下面3个不等式有什么相同点与
不同点?
(1)
>2;
(2)
<0;
(3)
<-1
3个不等式相同的特点是:不等号左边都
是 ;不同点是:不等号及不等号右
边分别是 , , .
2
0
-1
3x+2
认真阅读课本第96至97页的内容,完成下面练习并体验知识点的形成过程.
研读课文
2、你能从函数的角度对这3个不等式进行解释吗?(1)3x+2>2 (2)3x+2<0 (3)3x+2<-1
的取值范围.
的函数值分别为 、
、 时,求
自变量
从“数”上:这3个不等式相当
于在一次函数
小于-1
大于2
小于0
3x+2>2
3x+2<0
3x+2
(求自变量x的取值范围)
研读课文
从“形”上:在直线
上取纵坐标分别
满足条件 、 、 的点,看他
们的横坐标分别满足什么条件
大于2
小于0
小于-1
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
(求x的取值范围)
(1)3x+2>2
(2)3x+2<0
(3)3x+2<-1
练一练
<0.
时,
当
1、已知函数
,当
时,
>0;
> 3
< 3
2、已知一次函数
的图象如图所
>0的解集是( )
示,则不等式
A.x>-2? B.x<-2
C.x>-1???? D.x<-1
B
轴上方时
上的点在
3、直线
A.x>1?? B.x≥1 C.x<1?? D.x≤1
对应的自变量的范围是( ? )
4、已知直线
(-2,0),
则关于不等式
<0
集是 (? )
的解
A.x>-2? ??B.x≥-2
C.x<-2???? D.x≤-2
轴的交点为
与
C
A
归纳总结
一次函数问题
y取一个常数值
一元一次方程问题
一元一次方程问题
确定ax+b是否相同,方程右边的值作为
函数值y(纵坐标)所对应的x(横坐标)的值
一次函数问题
一次函数问题
一元一次不等式问题
y取一个范围
一元一次不等式问题
一次函数问题
确定ax+b是否相同,不等式(“>”或“<”)右边的值作为函数值y(纵坐标)所对应的x(横坐标)的取值范围
(求自变量x的值)
(求方程x的解)
(求自变量x的取值范围)
(求x的取值范围)
一次函数问题
一元一次不等式问题
y取一个范围
一元一次不等式问题
一次函数问题
(求自变量x的取值范围)
(求x的取值范围)
巩固训练
的值大于0?
1、当自变量
为何值时,函数
分析:“函数
的值大于0”就是y大于0,
即,
解:据题意得
所以,当自变量
时,函数
的值大于0。
2、直线 与 轴的交点是(? )
A.(0,-3)???B.(-3,0)????
C.(0,3)??? D.(0,-3)
B
轴下方?
的值满足_______时,直线
3、当自变量
上的点在
x<2
4、试根据函数
的性质或图象,
确定
取何值时:
(1)
>0;
<0
(2)
分析:根据函数图象在x轴下方的部分,y<0,
与x轴的交点y=0,在x轴上方的部分,y>0
解:令 ,解得,
∵函数 中k=3>0,
∴y随x的增大而增大,
∴(1)当x>5时,y>0;
(2)当x<5时,y<0.
5、根据图象,你能直接说出一元一次方程 的解吗?
解:由图象可知χ+3=0的
解为χ= ?3.
3
x
y
0
-3
从“形”上看
直线y=x+3的图象与x轴交点坐标为 (_-3_,_0_ ),这说明方程χ+3=0的解是x=_-3_)
Thank you!
谢谢同学们的努力!
