八年级数学下册课件-19.3 课题学习 选择方案7-人教版(共13张ppt)
文档属性
| 名称 | 八年级数学下册课件-19.3 课题学习 选择方案7-人教版(共13张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览


文档简介
19.3 课题学习 选择方案
第十九章 一次函数
人教版
八年级
下册
复习旧知
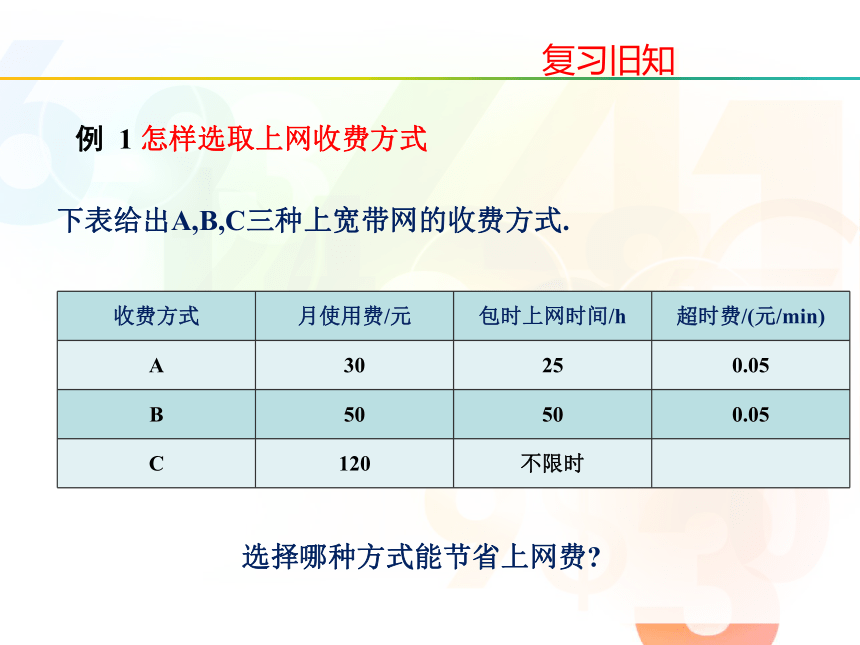
例 1 怎样选取上网收费方式
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
选择哪种方式能节省上网费?
下表给出A,B,C三种上宽带网的收费方式.
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
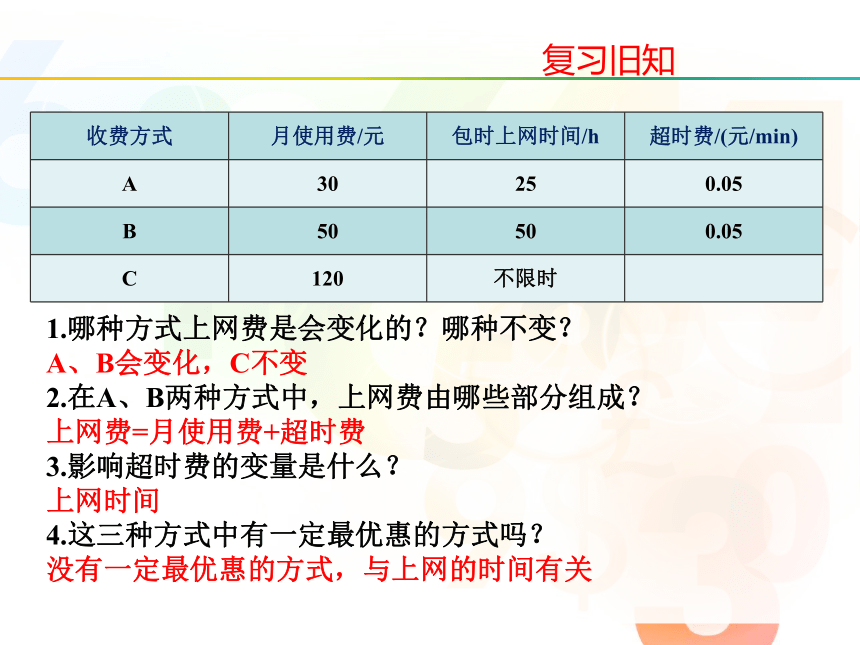
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
复习旧知
引入新课
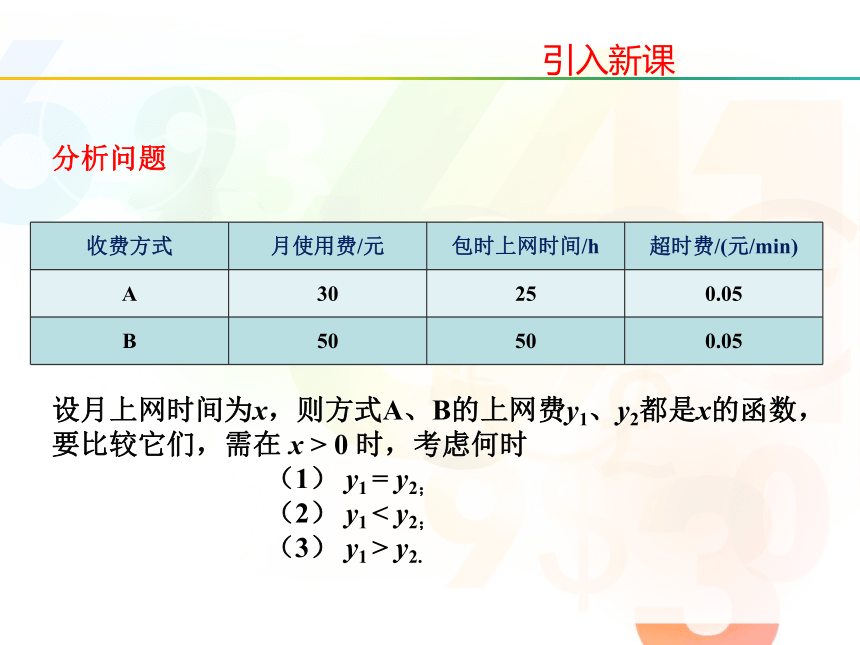
分析问题
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
设月上网时间为x,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在 x > 0 时,考虑何时
(1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
超时费不是一定有的,只有在上网时间超过25h时才会产生.
上网费=月使用费+超时费
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
讲授新课
讲授新课
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
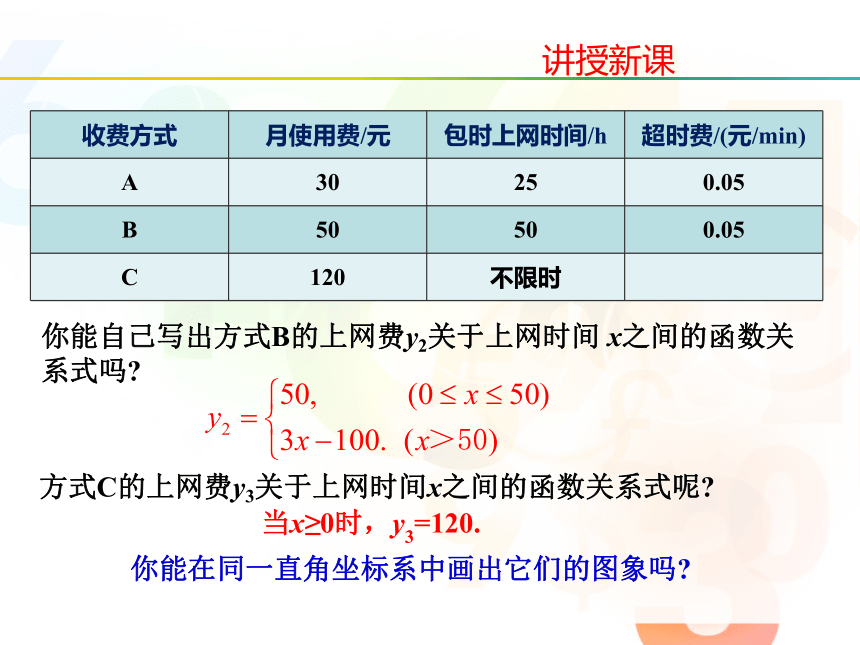
你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗?
方式C的上网费y3关于上网时间x之间的函数关系式呢?
你能在同一直角坐标系中画出它们的图象吗?
当x≥0时,y3=120.
当上网时间__________时,
选择方式A最省钱.
当上网时间 时,
选择方式B最省钱.
当上网时间_________时,
选择方式C最省钱.
讲授新课
货物调动问题中的方案选择(重难点)
例 2:某乡 A、B 两村盛产柑橘,A 村有柑橘 300 吨,B 村
有柑橘 200 吨.现将这些柑橘运到 C、D 两个冷藏仓库,已知 C
仓库可储存 240 吨,D 仓库可储存 260 吨;从 A 村运往 C、D
两处的费用分别为每吨 20 元和 25 元,从 B 村运往 C、D 两处
的费用分别为每吨 15 元和 18 元.怎样调运总运费最小?
的柑橘为 x 吨,其余变量可列表如下:
思路导引:本题中含有多个变量,可设从 A 村运往 C 仓库
讲授新课
收 地
运 地
C
D
总计
A
x 吨
300-x
300 吨
B
240-x
x-40
200 吨
总计
240 吨
260 吨
500 吨
再根据表中四个变量均为非负数,求出 x 的取值范围.列
出总运费关于 x 的函数,再根据一次函数的性质求解.
讲授新课
解:设从 A 村运往 C 仓库的柑橘重量为 x 吨,则由 A 村运往
D 仓库(300-x)吨,由 B 村运往 C 仓库(240-x)吨,由 B 村运往 D
仓库(x-40)吨.
设总运费为 y 元,y =20x +25×(300 -x) +15×(240 -x) +
18×(x-40),即 y=-2x+10 380(40≤x≤240).
由一次函数的性质可知,当 x=240 时,y 最小,y 的最小值是
-2×240+10 380=9 900(元).
故从 A 村运往 C 仓库 240 吨,运往 D 仓库 60 吨,且 B 村 200
吨全部运往 D 仓库时,总运费最小,最小运费是 9 900 元.
讲授新课
强化训练
目的地
运 费
(元/台)
发货地
C
D
A
100
200
B
90
150
A 市和 B 市分别有某种库存机器 12 台和 6 台,现决定
支援 C 村 10 台,D 村 8 台,机器运费如下表:
(1)设完成调运任务所需的总运费为 y 元,B 市运往 C 村机
器 x 台,求出 y 与 x 的函数关系式及自变量 x 的取值范围;
(2)求调运的最低费用.
解:(1)y=100×(10-x)+200×[12-(10-x)]+90x+
150×(6-x)=40x+2 300(0≤x≤6 且 x 为整数).
(2)∵k=40>0,∴y 随 x 的增大而增大.
∴当 x=0 时,y最小=2 300 元,
即最低费用为 2 300 元.
讲授新课
本节课主要学习了方案设计问题。在解决含有多个变量
的问题时,可以分析这些变量之间的关系,从中选取一
个取值能够影响其他变量的值的变量作为自变量。然后
根据问题的条件寻求可以反映实际问题的函数,以此作
为解决问题的数学模型。
课堂小结
第十九章 一次函数
人教版
八年级
下册
复习旧知
例 1 怎样选取上网收费方式
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
选择哪种方式能节省上网费?
下表给出A,B,C三种上宽带网的收费方式.
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
复习旧知
引入新课
分析问题
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
设月上网时间为x,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在 x > 0 时,考虑何时
(1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
超时费不是一定有的,只有在上网时间超过25h时才会产生.
上网费=月使用费+超时费
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
讲授新课
讲授新课
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗?
方式C的上网费y3关于上网时间x之间的函数关系式呢?
你能在同一直角坐标系中画出它们的图象吗?
当x≥0时,y3=120.
当上网时间__________时,
选择方式A最省钱.
当上网时间 时,
选择方式B最省钱.
当上网时间_________时,
选择方式C最省钱.
讲授新课
货物调动问题中的方案选择(重难点)
例 2:某乡 A、B 两村盛产柑橘,A 村有柑橘 300 吨,B 村
有柑橘 200 吨.现将这些柑橘运到 C、D 两个冷藏仓库,已知 C
仓库可储存 240 吨,D 仓库可储存 260 吨;从 A 村运往 C、D
两处的费用分别为每吨 20 元和 25 元,从 B 村运往 C、D 两处
的费用分别为每吨 15 元和 18 元.怎样调运总运费最小?
的柑橘为 x 吨,其余变量可列表如下:
思路导引:本题中含有多个变量,可设从 A 村运往 C 仓库
讲授新课
收 地
运 地
C
D
总计
A
x 吨
300-x
300 吨
B
240-x
x-40
200 吨
总计
240 吨
260 吨
500 吨
再根据表中四个变量均为非负数,求出 x 的取值范围.列
出总运费关于 x 的函数,再根据一次函数的性质求解.
讲授新课
解:设从 A 村运往 C 仓库的柑橘重量为 x 吨,则由 A 村运往
D 仓库(300-x)吨,由 B 村运往 C 仓库(240-x)吨,由 B 村运往 D
仓库(x-40)吨.
设总运费为 y 元,y =20x +25×(300 -x) +15×(240 -x) +
18×(x-40),即 y=-2x+10 380(40≤x≤240).
由一次函数的性质可知,当 x=240 时,y 最小,y 的最小值是
-2×240+10 380=9 900(元).
故从 A 村运往 C 仓库 240 吨,运往 D 仓库 60 吨,且 B 村 200
吨全部运往 D 仓库时,总运费最小,最小运费是 9 900 元.
讲授新课
强化训练
目的地
运 费
(元/台)
发货地
C
D
A
100
200
B
90
150
A 市和 B 市分别有某种库存机器 12 台和 6 台,现决定
支援 C 村 10 台,D 村 8 台,机器运费如下表:
(1)设完成调运任务所需的总运费为 y 元,B 市运往 C 村机
器 x 台,求出 y 与 x 的函数关系式及自变量 x 的取值范围;
(2)求调运的最低费用.
解:(1)y=100×(10-x)+200×[12-(10-x)]+90x+
150×(6-x)=40x+2 300(0≤x≤6 且 x 为整数).
(2)∵k=40>0,∴y 随 x 的增大而增大.
∴当 x=0 时,y最小=2 300 元,
即最低费用为 2 300 元.
讲授新课
本节课主要学习了方案设计问题。在解决含有多个变量
的问题时,可以分析这些变量之间的关系,从中选取一
个取值能够影响其他变量的值的变量作为自变量。然后
根据问题的条件寻求可以反映实际问题的函数,以此作
为解决问题的数学模型。
课堂小结
