八年级数学下册课件-20.2 数据的波动程度7-人教版(共15张ppt)
文档属性
| 名称 | 八年级数学下册课件-20.2 数据的波动程度7-人教版(共15张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 415.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览






文档简介
怎样才能衡量整个一组数据的波动大小呢?
20.2.2 方差
例1:在一次芭蕾舞的比赛中,甲,乙两个芭蕾舞团表演了舞剧<天鹅舞>,参加表演的女演员的身高(单位:cm)分别是
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞女演员的身高更齐整?
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
单击此处编辑母版标题样式
*
*
*
单击此处编辑母版副标题样式
20.2 数据的波动
20.2.1 极差
极差=最大值-最小值
10
12
16
11
9
12
13
13
2002年
12
9
8
6
22
14
13
12
2001年
2月28日
2月27日
2月26日
2月25日
2月24日
2月23日
2月22日
2月21日
该表显示:上海2001年2月下旬和2002年同期的每日最高气温
问:2001年2月下旬上海的气温的极差是多少?
2002年同期的上海的气温的极差又是多少?
22-6=16
16-9=7
结论:2001年的2月下旬的气温变化幅度大于2002年同期的变化幅度.
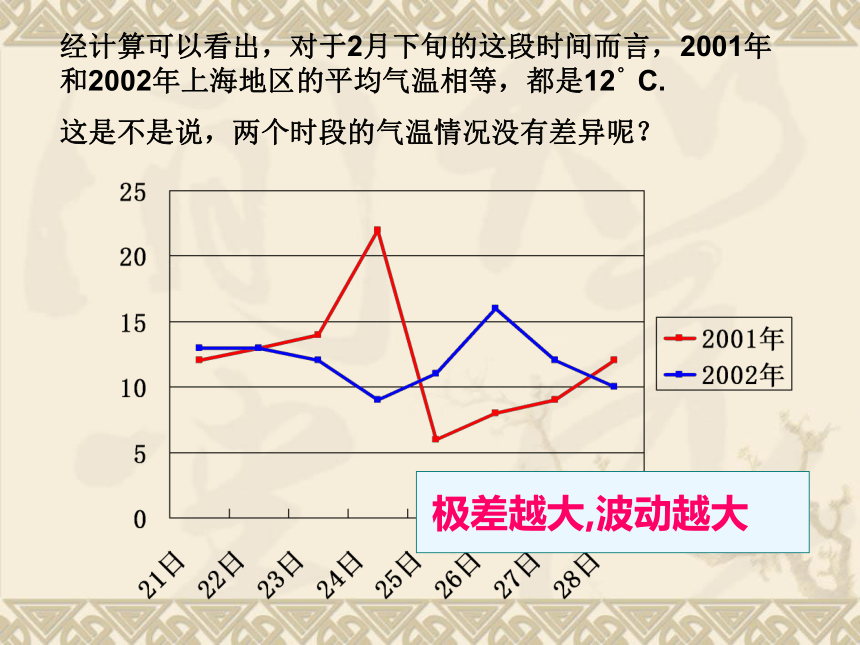
经计算可以看出,对于2月下旬的这段时间而言,2001年和2002年上海地区的平均气温相等,都是12。C.
这是不是说,两个时段的气温情况没有差异呢?
极差越大,波动越大
怎样定量地计算整个波动大小呢?
甲:10 7 7 7 7 7 4 7 7 7
乙: 9 6 5 9 8 5 5 9 5 9
极差是最简单的一种度量数据波动情况的量,但只能反映数据的波动范围,不能衡量每个数据的变化情况,而且受极端值的影响较大.
各 数据与平均数的差的平方的平均数叫做这批数据的方差。公式为:
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况。这个结果通常称为方差。
10
12
16
11
9
12
13
13
2002年
12
9
8
6
22
14
13
12
2001年
2月28日
2月27日
2月26日
2月25日
2月24日
2月23日
2月22日
2月21日
以上气温问题中8次气温的变化的方差的计算式是:
方差公式:
发现:
方差越小,波动越小.
方差越大,波动越大.
练习:
1。样本方差的作用是()
( A)表示总体的平均水平 (B)表示样本的平均水平
(C)准确表示总体的波动大小 (D)表示样本的波动大小
2. 在样本方差的计算公式
数字10 表示( )数字20表示( )
3。样本5、6、7、8、9、的方差是( ) .
4.一个样本的方差是零,若中位数是a,则它的平均数是( )
(A)等于 a (B)不等于a (C)大于a ( D)小于a
5. 从种植密度相同的甲、乙两块玉米地里,各抽取一个容量足够大
的 样本,分别统计单株玉米的产量.结果: = , < ,
下列 给出对两块玉米地的五种估计,哪几种是有道理的?
(1)甲块田平均产量较高(2)甲块田单株产量比较稳 定(3)两块田平均产量大约相等 (4)两块田总产量大约相等 (5)乙块田总产量较高
提高题:观察和探究。
(1)观察下列各组数据并填空
A.1、2、3、4、5
B.11、12、13、14、15
C.10、20、30、40、50
D.3 、5、7、9、11
(2)分别比较 A与 B 、 A与C、 A与D的计算结果,你能发现什么规律?
(3)若已知一组数据 的平均数是 ,方
差是 ,那么另一组数据
的平均数是 ( ) , 方差是( ).
的平均数是——,方差 是——。
=
=
=
=
=
=
=
=
,
…
…
规律;有两组数据,设其平均数分别为 ,
方差分别为 ,
(!) 当第二组每个数据比第一组每个数据增加m个单位时, 则有 = +m, =
(2) 当第二组每个数据是的第一组每个数据 n
倍时, 则有 =n , =
(3) 当第二组每个数据是的第一组每个数据 n
倍加 m 时,则有 = n , =
20.2.2 方差
例1:在一次芭蕾舞的比赛中,甲,乙两个芭蕾舞团表演了舞剧<天鹅舞>,参加表演的女演员的身高(单位:cm)分别是
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞女演员的身高更齐整?
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
单击此处编辑母版标题样式
*
*
*
单击此处编辑母版副标题样式
20.2 数据的波动
20.2.1 极差
极差=最大值-最小值
10
12
16
11
9
12
13
13
2002年
12
9
8
6
22
14
13
12
2001年
2月28日
2月27日
2月26日
2月25日
2月24日
2月23日
2月22日
2月21日
该表显示:上海2001年2月下旬和2002年同期的每日最高气温
问:2001年2月下旬上海的气温的极差是多少?
2002年同期的上海的气温的极差又是多少?
22-6=16
16-9=7
结论:2001年的2月下旬的气温变化幅度大于2002年同期的变化幅度.
经计算可以看出,对于2月下旬的这段时间而言,2001年和2002年上海地区的平均气温相等,都是12。C.
这是不是说,两个时段的气温情况没有差异呢?
极差越大,波动越大
怎样定量地计算整个波动大小呢?
甲:10 7 7 7 7 7 4 7 7 7
乙: 9 6 5 9 8 5 5 9 5 9
极差是最简单的一种度量数据波动情况的量,但只能反映数据的波动范围,不能衡量每个数据的变化情况,而且受极端值的影响较大.
各 数据与平均数的差的平方的平均数叫做这批数据的方差。公式为:
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况。这个结果通常称为方差。
10
12
16
11
9
12
13
13
2002年
12
9
8
6
22
14
13
12
2001年
2月28日
2月27日
2月26日
2月25日
2月24日
2月23日
2月22日
2月21日
以上气温问题中8次气温的变化的方差的计算式是:
方差公式:
发现:
方差越小,波动越小.
方差越大,波动越大.
练习:
1。样本方差的作用是()
( A)表示总体的平均水平 (B)表示样本的平均水平
(C)准确表示总体的波动大小 (D)表示样本的波动大小
2. 在样本方差的计算公式
数字10 表示( )数字20表示( )
3。样本5、6、7、8、9、的方差是( ) .
4.一个样本的方差是零,若中位数是a,则它的平均数是( )
(A)等于 a (B)不等于a (C)大于a ( D)小于a
5. 从种植密度相同的甲、乙两块玉米地里,各抽取一个容量足够大
的 样本,分别统计单株玉米的产量.结果: = , < ,
下列 给出对两块玉米地的五种估计,哪几种是有道理的?
(1)甲块田平均产量较高(2)甲块田单株产量比较稳 定(3)两块田平均产量大约相等 (4)两块田总产量大约相等 (5)乙块田总产量较高
提高题:观察和探究。
(1)观察下列各组数据并填空
A.1、2、3、4、5
B.11、12、13、14、15
C.10、20、30、40、50
D.3 、5、7、9、11
(2)分别比较 A与 B 、 A与C、 A与D的计算结果,你能发现什么规律?
(3)若已知一组数据 的平均数是 ,方
差是 ,那么另一组数据
的平均数是 ( ) , 方差是( ).
的平均数是——,方差 是——。
=
=
=
=
=
=
=
=
,
…
…
规律;有两组数据,设其平均数分别为 ,
方差分别为 ,
(!) 当第二组每个数据比第一组每个数据增加m个单位时, 则有 = +m, =
(2) 当第二组每个数据是的第一组每个数据 n
倍时, 则有 =n , =
(3) 当第二组每个数据是的第一组每个数据 n
倍加 m 时,则有 = n , =
