苏科版数学八年级上册 4.1 平方根 课件(18张)
文档属性
| 名称 | 苏科版数学八年级上册 4.1 平方根 课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 192.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
4.1
平方根
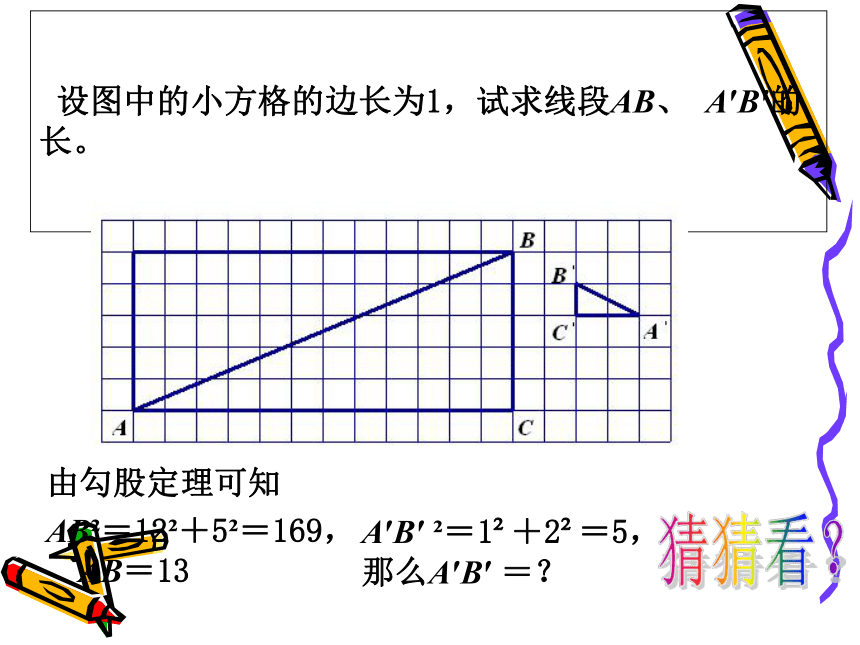
设图中的小方格的边长为1,试求线段AB、
A′B′的长。
由勾股定理可知
AB?=12?+5?=169,
AB=13
A′B′
?=1?+2?=5,
那么A′B′
=?
猜猜看?
2.
一间面积为9m?的正方形房间,它的边长x是多少?
如果正方形房间的面积是15m?、16m?、20m?,它的边长x又应该是多少呢?
要解决以上问题,我们就要研究当x2=a时,x是什么数?
当x2=4,
因为(
)
?=4,(
)?=4,所以x=(
)
当x2=100,
因为(
)?=100,(
)?=100,所以x=(
)
当x2=169,
因为(
)?=169,(
)?=169,所以x=(
)
可以看出使x2=a(a>0)成立的数有
个
,它们之间有什么关系?
如果x?=a
,那么x叫做a的平方根,也称为二次方根.
(a
≥0)
填空:
(
)叫做4的平方根.
(
)叫做100的平方根.
(
)叫做169的平方根.
概念
如果
x2=a(a
≥0)
,那么
x
叫做
a
的平方根.
判断:
1.
3
是
9
的平方根.
()
2.
-3
是
9
的平方根.()
3.
16
的平方根
是4.()
4.
5
是
35
的平方根.()
5.
36
的平方根是±6.()
概念
如果
x2=a(a
≥0)
,那么
x
叫做
a
的平方根.
这两个平方根合起来记作“±
”,
读作“正、负根号a
”.
一个正数的平方根有2个,它们互为相反数.
一个正数
a
的正的平方根,记作“
”.
一个正数
a
的负的平方根,记作“-
”.
例如,2的平方根记作“±
”,读作
“正、负根号2”.
81的平方根记作“
± ”,读作
“正、负根号81”.
( )2=9,
( )2=25,
( )2= ,
( )2=0,
( )2=- ,
( )2=-4.
你有什么发现?
在下列各括号中能填写适当的数使等式成立吗?如果能,请填写;如果不能,请说明理由,并与同学交流.
一个正数有两个平方根,它们互为相反数;
广而告之
求一个数的平方根的运算叫做开平方.
0的平方根是0;
负数没有平方根.
1.A′B′
?=1?+2?=5,那么A′B′
=?
2.一间面积为15m?/20m?的正方形房间,它的边长x是多少?
解决问题
例1
求下列各数的平方根:
(1)25
;
(2)
;
(3)15
;
(4)0.09
(5)81
(6)0.81
例题精讲
例2
求下列各式中的
x.
(1)
x?=196
;
(2)
5x?-10=
0
;
(3)
36(x-3)?-25=0
;
1·今天我们学习了什么内容?
2·开平方运算与平方运算有什么联系?有什么区别?
课
堂
小
结
由于平方与开平方互为逆运算,
因此可以通过平方运算来求
一个数的平方根,
也可以通过平方运算
来检验一个数是不是
另一个数的平方根。
4.1 平方根(1)
拓展提高
2.已知一个正数的平方根是3x-2
和5x+6,则这个数是(
)
1.若x2=16,则5-x的平方根等于(
)
思考:
已知5x-1的平方根是±3,4x+2y+1的平方根是±1,求4x-2y的平方根.
谢
谢!
4.1
平方根
设图中的小方格的边长为1,试求线段AB、
A′B′的长。
由勾股定理可知
AB?=12?+5?=169,
AB=13
A′B′
?=1?+2?=5,
那么A′B′
=?
猜猜看?
2.
一间面积为9m?的正方形房间,它的边长x是多少?
如果正方形房间的面积是15m?、16m?、20m?,它的边长x又应该是多少呢?
要解决以上问题,我们就要研究当x2=a时,x是什么数?
当x2=4,
因为(
)
?=4,(
)?=4,所以x=(
)
当x2=100,
因为(
)?=100,(
)?=100,所以x=(
)
当x2=169,
因为(
)?=169,(
)?=169,所以x=(
)
可以看出使x2=a(a>0)成立的数有
个
,它们之间有什么关系?
如果x?=a
,那么x叫做a的平方根,也称为二次方根.
(a
≥0)
填空:
(
)叫做4的平方根.
(
)叫做100的平方根.
(
)叫做169的平方根.
概念
如果
x2=a(a
≥0)
,那么
x
叫做
a
的平方根.
判断:
1.
3
是
9
的平方根.
()
2.
-3
是
9
的平方根.()
3.
16
的平方根
是4.()
4.
5
是
35
的平方根.()
5.
36
的平方根是±6.()
概念
如果
x2=a(a
≥0)
,那么
x
叫做
a
的平方根.
这两个平方根合起来记作“±
”,
读作“正、负根号a
”.
一个正数的平方根有2个,它们互为相反数.
一个正数
a
的正的平方根,记作“
”.
一个正数
a
的负的平方根,记作“-
”.
例如,2的平方根记作“±
”,读作
“正、负根号2”.
81的平方根记作“
± ”,读作
“正、负根号81”.
( )2=9,
( )2=25,
( )2= ,
( )2=0,
( )2=- ,
( )2=-4.
你有什么发现?
在下列各括号中能填写适当的数使等式成立吗?如果能,请填写;如果不能,请说明理由,并与同学交流.
一个正数有两个平方根,它们互为相反数;
广而告之
求一个数的平方根的运算叫做开平方.
0的平方根是0;
负数没有平方根.
1.A′B′
?=1?+2?=5,那么A′B′
=?
2.一间面积为15m?/20m?的正方形房间,它的边长x是多少?
解决问题
例1
求下列各数的平方根:
(1)25
;
(2)
;
(3)15
;
(4)0.09
(5)81
(6)0.81
例题精讲
例2
求下列各式中的
x.
(1)
x?=196
;
(2)
5x?-10=
0
;
(3)
36(x-3)?-25=0
;
1·今天我们学习了什么内容?
2·开平方运算与平方运算有什么联系?有什么区别?
课
堂
小
结
由于平方与开平方互为逆运算,
因此可以通过平方运算来求
一个数的平方根,
也可以通过平方运算
来检验一个数是不是
另一个数的平方根。
4.1 平方根(1)
拓展提高
2.已知一个正数的平方根是3x-2
和5x+6,则这个数是(
)
1.若x2=16,则5-x的平方根等于(
)
思考:
已知5x-1的平方根是±3,4x+2y+1的平方根是±1,求4x-2y的平方根.
谢
谢!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
