第五章《相交线与平行线》复习+三套能力测试题及答案
文档属性
| 名称 | 第五章《相交线与平行线》复习+三套能力测试题及答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 709.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-08 00:00:00 | ||
图片预览


文档简介
相交线与平行线
一.基本知识:
1.相交线 2.邻补角 对顶角 3.垂线
4.同位角 内错角 同旁内角的定义 6.平行的定义
7.平行线的判定 性质 8.命题与定理的定义 9.平移
(一)..两直线的位置关系:相交(垂直) 平行
(二).各类角的概念及性质
1.同位角 内错角 同旁内角的定义
2.邻补角和对顶角的性质
(1)邻补角互补
(2)对顶角相等
注:“同”指两角位于第三直线的同侧,“错”指两角位于第三直线两侧
“内”指两角位于两被截直线之间
(三).垂线 点到直线的距离
1.垂线的概念:两条直线相交,若其所形成的四个角中有一个角等于90°,
则称这两条直线互相垂直,其中一条直线叫做另一条直线的
垂线,他们的交点叫做垂足
注:(1)垂直是相交的一种特殊情形
(2)两直线垂直必具备两个要点:A.相交 B.有一个角为直角
2.垂线的性质:
(1)在平面门内,过一点有且只有一条直线与已知直线垂直
(2)连接直线外一点与直线上各点的所有县段中,垂线段最短
(四).平行线
1.平行线的概念:在同一平面内,不相交的两条直线叫做平行线
注:平行的前提是两直线在同一平面内
2.平行公理
(1)经过直线外一点,有且只有一条直线与这条直线平行
(2)如果两条直线都与第三条直线平行,那么着两条直线也互相平行,
即如果a∥b,b∥c,那么a∥c
3.平行线的性质
(1)两条平行直线被第三条直线所截,同位角相等
(2)两条平行直线被第三条直线所截,内错角相等
(3)两条平行直线被第三条直线所截,同旁内角互补
4.平行线的距离:同时垂直于两条平行线,并且夹在平行线间的线段的长度,
叫做这两条平行线间的距离
5.平行线的判定
如果两直线被第三条直线所截:
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
二 .典型例题
例1.如图1所示,直线AB.CD相交于点O,∠AOC=40°,求∠COB.∠BOD
∠AOD的度数?
解:由邻补角的定义可得
∠COB=180°—∠AOC=180°—40°=140°
由对顶角相等可得
∠BOD=∠AOC=40°
∠AOD=∠COB=140°
例2.如图2所示,已知∠AOB于∠BOC互为邻补角,OD平分∠AOB,
OE⊥OD,试问:OE是否平分∠COB?为什么?
点拔:在分析∠BOE和∠COE的关系时,可以利用余角的
性质,通过考虑余角,∠BOD和∠AOD的关系,从
而得出结论
解:OE平分∠COB的理由如下:
∵∠AOD+∠BOD+∠BOE+∠ COE=180°,OE⊥OD
∴∠BOE+∠BOD=90°
∵OD平分∠AOB,
∴∠AOD=∠BOD
∴∠AOD+∠BOE=90°
∴∠BOD+∠COE=90° E B
D
∴∠BOE=∠COE,即OE平分∠COB
C O A
图2
例3.如图3所示BE∥DF,AB⊥BE,CD⊥DF,垂足为点B,D,试说明AB∥CD。
点拔:欲说明AB∥CD,只需说明∠ABD=∠CDG,有已知条件可以说明
解:∵BE∥DF(已知)
∴∠DFG=∠DBE(两直线平行,同位角相等)
又∵AB⊥BE,CD⊥DF(已知) A E C F
∴∠ABE=∠CDF=90°(垂直定义)
∴∠ABE+∠DBE=∠CDF+∠DGF(等式性质)
∴∠ABD=∠CDG
B D G
∴AB∥CD(同位角相等,两直线平行)
三.适时训练
一. 选择题:
1. 如果两个角的一边在同一条直线上,另一边互相平行,那么这两个角( )
A. 相等或互补 B. 互补 C. 相等 D. 相等且互与
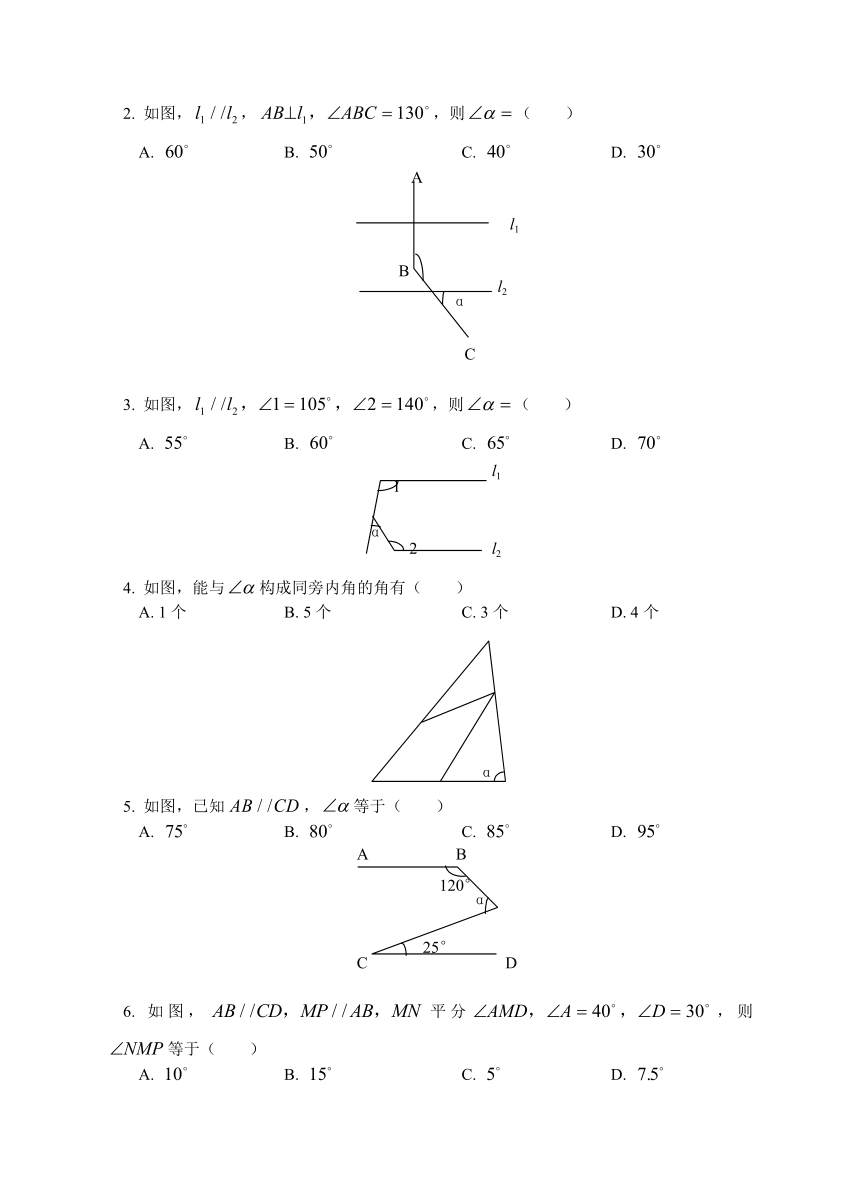
2. 如图,,,则( )
A. B. C. D.
A
l1
B
l2
α
C
3. 如图,,则( )
A. B. C. D.
l1
1
α
2 l2
4. 如图,能与构成同旁内角的角有( )
A. 1个 B. 5个 C. 3个 D. 4个
α
5. 如图,已知,等于( )
A. B. C. D.
A B
120°
α
25°
C D
6. 如图,平分,则等于( )
A. B. C. D.
B M C
A N P D
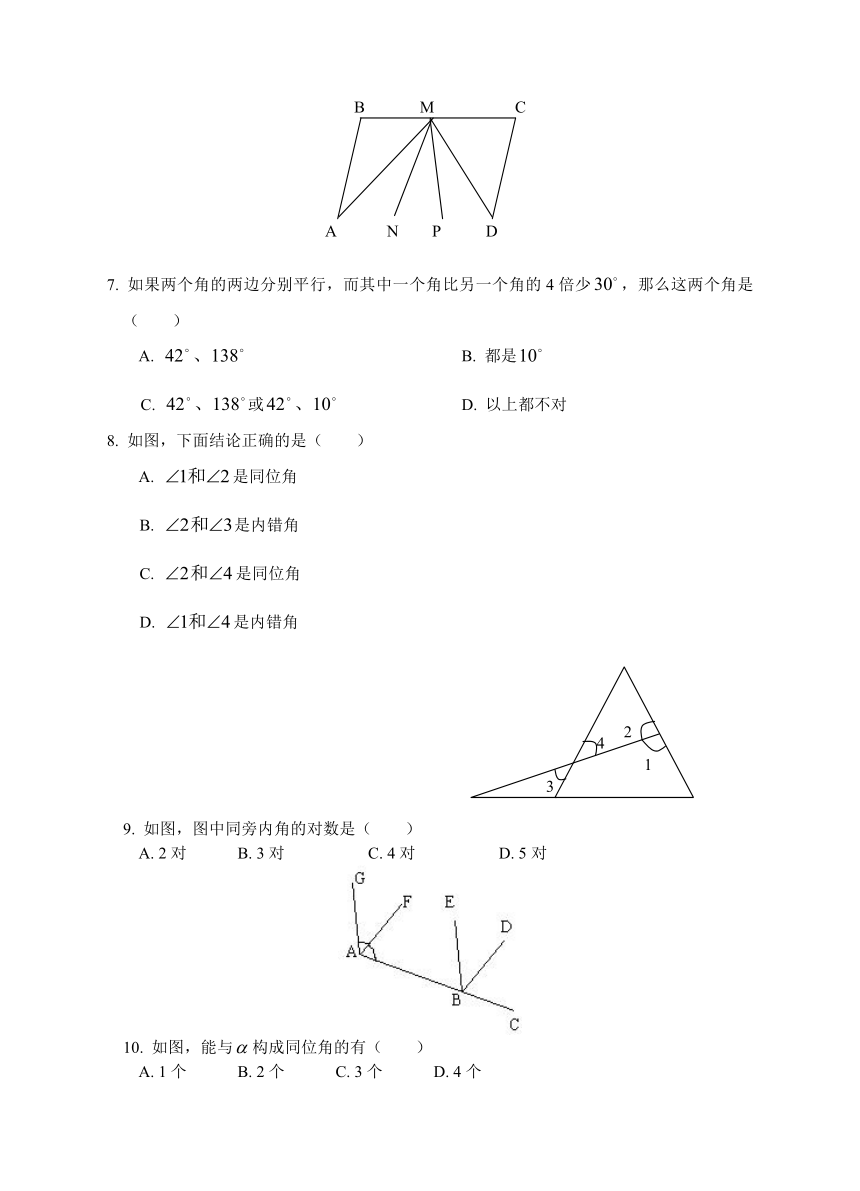
7. 如果两个角的两边分别平行,而其中一个角比另一个角的4倍少,那么这两个角是( )
A. B. 都是
C. 或 D. 以上都不对
8. 如图,下面结论正确的是( )
A. 是同位角
B. 是内错角
C. 是同位角
D. 是内错角
9. 如图,图中同旁内角的对数是( )
A. 2对 B. 3对 C. 4对 D. 5对
10. 如图,能与构成同位角的有( )
A. 1个 B. 2个 C. 3个 D. 4个
α
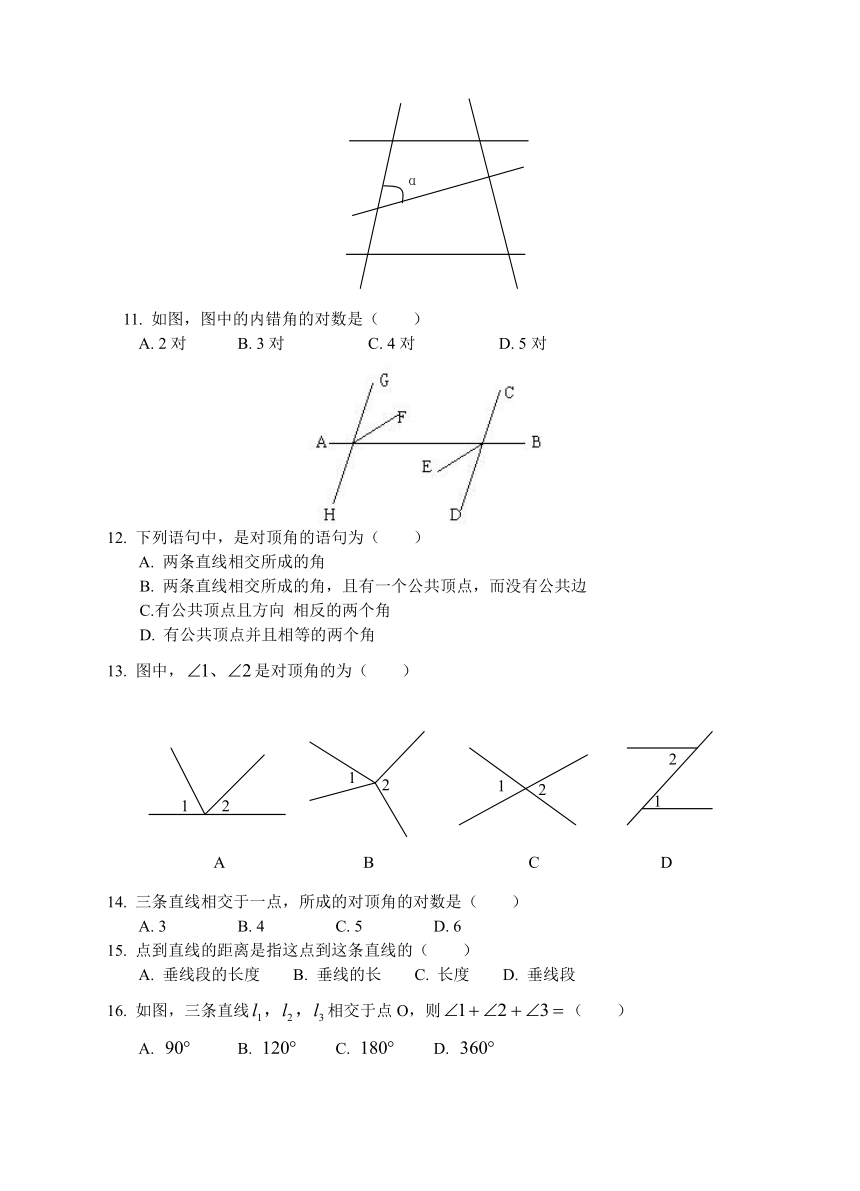
11. 如图,图中的内错角的对数是( )
A. 2对 B. 3对 C. 4对 D. 5对
12. 下列语句中,是对顶角的语句为( )
A. 两条直线相交所成的角
B. 两条直线相交所成的角,且有一个公共顶点,而没有公共边
C.有公共顶点且方向 相反的两个角
D. 有公共顶点并且相等的两个角
13. 图中,是对顶角的为( )
1 2
A B C D
14. 三条直线相交于一点,所成的对顶角的对数是( )
A. 3 B. 4 C. 5 D. 6
15. 点到直线的距离是指这点到这条直线的( )
A. 垂线段的长度 B. 垂线的长 C. 长度 D. 垂线段
16. 如图,三条直线相交于点O,则( )
A. B. C. D.
1 O 3
2 l1
l2
l3
17. 已知:,则的度数为( )
A. B. C. D. 不同于以上答案
二. 填空题:
1. 如图,图中1和E是______和________被_______所截的_______角;
2和3是_________和_________被___________所截的________角;
1和4是_________和________被________所截的_________角;
BCE和E是被_________所截的_______角。
E
A
1 2
4 3
B D C
2. 如图,1的同旁内角是_________,2的内错角是___________,图中共有______对同位角。
M G
A 4 B
E 3 H
2 1
C F D
N
3. 两个互为邻补角的角平分线___________;两个对顶角的角平分线形成___________。
4. 直线AB与CD互相垂直,垂足为O,P是直线CD上一点,则P到AB的距离是__________。
5. 如图1,直线AB、CD、EF都经过O点,并且已知,则__________,_________,________,______。
A F
C O D
E B
图1
6. 如图,直线AB、CD、EF相交于O,且,,则_______,__________。
C
E
A 2 O B
1
F
D
7. 如图:于D,,则__________。
23
A D B
8. 已知:如图,于D,,则________,______,__________。
C
F
1
A D B
E
9. 判断下列图形中,有没有对顶角,若有请写出哪两个角
1.
4
1 3
2.
1 4 8 7
2 3 5 6
9
12 10
11
2.
1 4 8 7
2 3 5 6
9
12 10
11
3.
1 2
3 4 7
5 6
4.
1
2
4.
1
2
EMBED Word.Picture.8 5.
1 4
2 3
三.解答题
1. 如图,直线AB、CD被EF所截,如果互补,且,那么的度数是多少?
C E
2
3 D
4
1 B
A
F
2. 已知:直线AD、BC交于O点,,求:的度数。
A
B O C
D
3. 已知:如图直线AB与CD交于O点,,求:的度数。
A
4 D
2 1
C 3
B
4. 已知:直线AB、EF相交于O点,于O点,,求
C
E
A O B
F
D
5. 如图,直线AB、CD、EF交于点O,是它的余角的2倍,,
且有,求的度数。
A
D
E O F
C
G B
6. 已知:如图,。求证:。
B
C
D
2 3
1
O A
证明:( )
( )
( )
( )
7. 已知:如图,COD是直线,。求证:A、O、B三点在同一条直线上。
A
C
1
2 O
3
D
B
证明:COD是一条直线( )
___________( )
( )
____________________
_______________( )
四. 证明题:
1. 已知:AB//CD,BD平分,DB平分,求证:DA//BC
2. 已知:如图,AB//CE,,求:的度数。
3. 已知:AB//CD,,求证:
4. 已知:如图,AB//CD,MN截AB、CD于E、F,且EG//FH,求证:
5. 已知:AF、BD、CE都为直线,B在直线AC上,E在直线DF上,且,,求证:。
6. 已知:如图,,求证:
7. 已知:如图,,且B、C、D在一条直线上。
求证:
A E
3
1 2
4
B C D
8. 已知:如图,,DE平分,BF平分,且。
求证:
D F C
A E B
9. 已知:如图,。
求证:
A B
1
E
F
2
C P D
10. 已知:如图,。
求证:
F
E
4
A G 1 B
5
3
6 2
C D
11. 如图,已知:CE=DF,AC=BD,1=2。求证:A=B。
12. 已知:如图,E、F分别是AB和CD上的点,DE、AF分别交BC于G、H,A=D,1=2,求证:B=C。
13. 如图,已知:AB//CD,求证:B+D+BED=(至少用三种方法)
【试题答案】
一. 选择题:
1-5 A C C B C 6-10 C .D DCC 11-17 DBCDACD
二. 填空题:
1. AD、EC、BE、同位角;AD、EC、AC、内错角;AB、CD、AD、内错角;EC、同旁内角。
2. 3和GEF;3和GEF;6
3. 互相垂直,一条直线
4. 线段OP的长度
5. 99,145,46。99
6. 63,117
7. =
8. 60,60,120
9. (1). 是对顶角
(2). 是对顶角。
(3). 是对顶角
( 4). 无 (5.) 无
三.解答题
1.
2.
3.
又
4.
又
5.
6. 已知,垂线性质,已知,垂线定义
7. 已知,180,平角定义,已知,,180,A、O、B三点在一条直线上,平角定义
四.证明题
1. ,BD平分,
BD平分,
2.
3.
又
4.
5. ,
6.
7. 证:
8. 证:平分
平分
9. 证:
又
即
10. 证:
11. 证明:
12. 证明:
即AC与BD互相平分。
13. 证明:
又
14. 证明:(1)连结BD。
(2)延长DE交AB延长线于F。
(3)过点E作EF//AB,
能力测试一
(一)判断题(每题2分,共10分)
1.过线段外一点画线段的中垂线……………………………………………………( )
2.如果两个角互为补角,那么它们的角平分线一定互相垂直……………………( )
3.两条直线不平行,同旁内角不互补………………………………………………( )
4.错误地判断一件事情的语句不叫命题……………………………………………( )
5.如图,AB∥CD,那么∠B+∠F+∠D=∠E+∠G………………………… ( )
(5题) (6题) (7题)
(二)填空题(每小题2分,共18分)
6.如图,当∠1=∠ 时,AB∥DC;当∠D+∠ =180°时,AB∥DC;当
∠B=∠ 时,AB∥CD.
7.如图,AB∥CD,AD∥BC,∠B=60°,∠EDA=50°.则∠CDF= .
8.如图,O是△ABC内一点,OD∥AB,OE∥BC,OF∥AC,∠B=45°,∠C=75°,则
∠DOE= ,∠EOF= ,∠FOD= .
(8题) (10题) (11题)
9.两个角的两边分别平行,其中一个角比另一个角的3倍少20°.则这两个角的度数分别是 .
10.如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,
∠B-∠D=24°,则∠GEF= .
11.如图,AD∥BC,点O在AD上,BO、CO分别平分∠ABC、∠DCB,若
∠A+∠D=m°.则∠BOC=______.
12.有一条直的等宽纸带,按图(1)折叠时,纸带重叠部分中的∠ = 度.
13.把命题“在同一平面内垂直于同一直线的两直线互相平行”写成“如果…那么…”的形式是:如果______________,那么_____________.
图(1) (15题) (16题)
(三)选择题(每小题3分,共21分)
15.如图,已知直线AB与CD相交于点O,OE⊥CD.垂足为O,则图中∠AOE和
∠DOB的关系是( )
(A)同位角 (B)对顶角 (C)互为补角 (D)互为余角
16.如图,CD⊥AB,垂足为D,AC⊥BC,垂足为C.图中线段的长能表示点到直线(或线段)距离的线段有…( )
(A)1条 (B)3条 (C)5条 (D)7条
17.若AO⊥BO,垂足为O,∠AOC︰∠AOB=2︰9,则∠BOC的度数等于……( )
(A)20° (B)70° (C)110° (D)70°或110°
18.下列命题中,真命题是……………………………………………………………( )
(A)同位角相等工 (B)同旁内角相等,两直线平行
(C)同旁内角互补 (D)同一平面内,平行于同一直线的两直线平行
20.如图,AD∥EF∥BC,且EG∥AC.那么图中与∠1相等的角(不包括∠1)的个数是( )
(A)2 (B)4 (C)5 (D)6
21.某人从A点出发向北偏东60°方向速到B点,再从B点出发向南偏西15°方向速到C点,则∠ABC等于…( )
(A)75° (B)105° (C)45° (D)135°
(四)解答题(本题5分)
22.根据命题“角平分线上的点到角的两边距离相等”,画出图形,并结合图形写出已知、求证(不证明).
五、计算题(第23、24题,每题5分.第25、26题每题6分,共22分)
23.如图,AB∥CD∥PN,∠ABC=50°,∠CPN=150°.求∠BCP的度数.
24.如图,∠CAB=100°,∠ABF=110°,AC∥PD,BF∥PE,求∠DPE的度数.
25.如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC.
求∠PAG的度数.
26.如图,AB∥CD,∠1=115°,∠2=140°,求∠3的度数.
(五)证明题(每题6分,共24分)
27.已知:如图.AB∥CD,∠B=∠C.求证:∠E=∠F.
28.已知:如图,AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.
29.已知:如图,AB∥CD,∠1=∠B,∠2=∠D.求证:BE⊥DE.
30.已知:如图,AB∥CD,请你观察∠E、∠B、∠D之间有什么关系,并证明你所得的结论.
参考答案
(一)判断题(每题2分,共10分)
1.过线段外一点画线段的中垂线……………………………………………………( )
【提示】线段外一点不一定在线段的中垂线上,所以过线段外一点画线段的垂线,不一定平分这条线段如图PQ⊥AB,垂足为O.但PQ不平分AB.【答案】×.
(1) (2) (3)
2.如果两个角互为补角,那么它们的角平分线一定互相垂直……………………( )
【提示】两个角互为补角时,这两个角可以是邻补角,也可以不是邻补角.当两角互补但不是邻补角时,则它们的角平分线不互相垂直.如图:∠AOB与∠AOC互补,OM平分∠AOC、ON平分∠AOB.显然OM与ON不垂直.【答案】×.
3.两条直线不平行,同旁内角不互补………………………………………………( )
【提示】如图,AB与CD不平行,EF与AB交于点G.与CD交于点H.
过点G作PQ∥CD.
∴ ∠QGF+∠GHD=180°.
∵ ∠BGF<∠QGF,
∴ ∠BGF+∠GHD<180°;
又 ∠PGH+∠GHC=180°,
∵ ∠AGH>∠PGH,
∴ ∠AGH+∠GHC>180°.
即两直线不平行,同旁内角不互补.【答案】√.
4.错误地判断一件事情的语句不叫命题…( )
【提示】判断一件事情的语句叫做命题.错误地判断得到的是假命题.假命题也是命题.
【答案】×.
5.如图,AB∥CD,那么∠B+∠F+∠D=∠E+∠G…………………………( )
【提示】过点E、F、G分别画EP∥AB,PQ∥AB,GM∥AB.
则AB∥EP∥FQ∥GM∥CD.
∴ ∠B=∠1,∠3=∠2,∠4=∠5,∠D=∠6.
∴ ∠B+∠3+∠4+∠D=∠1+∠2+∠5+∠6.
即∠B+∠EFG+∠D=∠BEF+∠FG(D) 【答案】√.
(二)填空题(每小题2分,共18分)
6.如图,当∠1=∠ 时,AB∥DC;当∠D+∠ =180°时,AB∥DC;当∠B=∠ 时,AB∥CD.
(6) (7) (8)
【提示】把题中的“AB∥CD”视作条件去找∠1的内错角、∠D的同旁内角和∠B的同位角.即得要填的角.【答案】4,DAB,5.
7.如图,AB∥CD,AD∥BC,∠B=60°,∠EDA=50°.则∠CDF= .
【提示】由AB∥CD,得∠DCF=∠B=60°,
由AD∥BC得∠ADC=∠DCF=60°,
∴ ∠ADE+∠ADC=50°+60°=110°,
∴ ∠CDF=180°-110°=70°. 【答案】70°.
8.如图,O是△ABC内一点,OD∥AB,OE∥BC,OF∥AC,∠B=45°,∠C=75°,则∠DOE= ,∠EOF= ,∠FOD= .
【提示】由OD∥AB,∠B=45°,得∠ODC=∠B=45°.
由OE∥DC,∠DOE+∠ODC=180°,∴ ∠DOE=180°-45°=135°.
同理可求∠EOF=105°.由周角的定义可求∠FOD=120°.
【答案】135°,105°,120°.
9.两个角的两边分别平行,其中一个角比另一个角的3倍少20°.则这两个角的度数分别是 .
【提示】如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
设一个角为x度.则另一个角为(3x-20)度.
依据上面的性质得,
3x-20=x,或3x-20+x=180°.
∴ x=10,或x=50.
当x=50时,3x-20=3×50-20=130.
【答案】10°、10°或50°、130°.
【点评】通过列方程(或方程组)解题是几何计算常用的方法.
10.如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,
∠B-∠D=24°,则∠GEF= .
(10) (11)
【提示】由AB∥EF∥CD,可知∠BED=∠B+∠D.
已知∠B+∠BED+∠D=192°.
∴ 2∠B+2∠D=192°,∠B+∠D=96°.
又 ∠B-∠D=24°.
于是可得关于∠B、∠D的方程组解得 ∠B=60°.
由AB∥EF知∠BEF=∠B=60°.因为EG平分∠BEF,所以∠GEF=∠BEF=30°.
【答案】30°.
11.如图,AD∥BC,点O在AD上,BO、CO分别平分∠ABC、∠DCB,若
∠A+∠D=m°.则∠BOC=______.
【提示】由AD∥BC,BO平分∠ABC,可知∠AOB=∠CBO=∠ABC.
同理∠DOC=∠BCO=∠DCB.
∵ AD∥BC,∴ ∠A+∠ABC=180°,∠D+∠DCB=180°,
∴ ∠A+∠D+∠ABC+∠DCB=360°.
∵ ∠A+∠D=m°,∴ ∠ABC+∠DCB=360°-m°.
∴ ∠AOB+∠DOC=(∠ABC+∠DCB)=(360°-m°)=180°-m°.
∴ ∠BOC=180°-(∠AOB+∠DOC)=180°-(180°-m°)=m°.
【答案】m°.
12.有一条直的等宽纸带,按图(1)折叠时,纸带重叠部分中的∠ =度.
【提示】裁一张等宽纸带按图示折叠,体会一下题目的含义.将等宽纸带展平,便得图(2).由此图可知∠DAC=30°.AB是∠C′AC的平分线.∴ ∠ =75°.【答案】75°.
图(2) 图(1)
【点评】解类似具有操作性的实际问题时,不妨动手做一做,从中感受一下题目的意义,进而将实际问题转化成数学问题.用数学知识解决实际问题.这样做不仅能培养我们抽象思维和空间想象能力,而且能提高我们解决实际问题的能力.
13.把命题“在同一平面内垂直于同一直线的两直线互相平行”写成“如果…那么…”的形式是:如果______________,那么_____________.
【答案】在同一平面内两条直线垂直于同一条直线,这两条直线互相平行.
14.如图,在长方体中,与面BCC′B′平行的面是面;与面BCC′B′垂直的面是,与棱A′A平行的面有,与棱A′A垂直的面有.
(15)
【答案】面ADD′A;面ABB′A′,面ABCD,面A′B′C′D′,面DCC′D′;
面DCC′D′,面BCC′B′;面ABCD,面A′B′C′D′.
(三)选择题(每小题3分,共21分)
15.如图,已知直线AB与CD相交于点O,OE⊥CD.垂足为O,则图中∠AOE和
∠DOB的关系是( )(A)同位角 (B)对顶角 (C)互为补角 (D)互为余角
【提示】由OE⊥CD,知:∠AOE与∠AOC互余.∠AOC与∠BOD是对顶角.所以∠AOE与∠DOB互为余角.【答案】D.
16.如图,CD⊥AB,垂足为D,AC⊥BC,垂足为C.图中线段的长能表示点到直线(或线段)距离的线段有…( )(A)1条 (B)3条 (C)5条 (D)7条
【提示】CD的长表示点C到AB的距离;AC的长表示点A到BC的距离;BC的长表示点B到AC的距离;AD的长表示点A到CD的距离,BD的长表示点B到CD的距离.共5条.【答案】C.
17.若AO⊥BO,垂足为O,∠AOC︰∠AOB=2︰9,则∠BOC的度数等于……( )
(A)20° (B)70° (C)110° (D)70°或110°
【提示】OC可在∠AOB内部,也可在∠AOB外部,如图可示,故有两解.
设∠AOC=2x°,则∠AOB=9x°.
∵ AO⊥BO, ∴ ∠AOB=90°.
∵ 9x=90°,x=10°,∠AOC=2x=20°.
(1)∠BOC=∠AOB-∠AOC=90°-20°=70°;
(2)∠BOC=∠AOB+∠AOC=90°+20°=110°.
【答案】D.
18.下列命题中,真命题是……………………………………………………………( )
(A)同位角相等工 (B)同旁内角相等,两直线平行
(C)同旁内角互补 (D)同一平面内,平行于同一直线的两直线平行
【提示】两直线不平行,则同位角不相等,同旁内角不互补,所以A、C错误,B也不一定成立.如图所示直线a、b被直线c所截.∠1=∠2,∠3=∠4.显然a与b不平行.
(18) (20) (21)
【答案】D.
19.直线AB∥CD,且与EF、GH相交成如图可示的图形,则共得同旁内角…( )
(A)4对 (B)8对 (C)12对 (D)16对
【提示】该图可分离出四个基本图形,如图所示.
第三条直线截两平行线,此时图形呈“”型,有同旁内角两对;
第三条直线截两相交线,此时图形呈“”型,有同旁内角六对.
故图中共有同旁内角2×2+6×2=16(对). 【答案】D.
20.如图,AD∥EF∥BC,且EG∥AC.那么图中与∠1相等的角(不包括∠1)的个数是……( )(A)2 (B)4 (C)5 (D)6
【提示】由AD∥EF∥BC,且EG∥AC可得:
∠1=∠DAH=∠FHC=∠HCG=∠EGB=∠GEH除∠1共5个.【答案】C.
21.某人从A点出发向北偏东60°方向速到B点,再从B点出发向南偏西15°方向速到C点,则∠ABC等于……………………………………………………………( )
(A)75° (B)105° (C)45° (D)135°
【提示】按要求画出图形再计算
∵ NA∥BS, ∴ ∠NAB=∠SBA=60°.
∵ ∠SBC=15°, ∴ ∠ABC=∠SBA-∠SBC=60°-15°=45°.【答案】C.
(四)解答题(本题5分)
22.根据命题“角平分线上的点到角的两边距离相等”,画出图形,并结合图形写出已知、求证(不证明).
【答案】已知:OC平分∠AOB,P是OC上任意一点.PD⊥OB,PE⊥OA,垂足分别是D、E.求证:PE=PD.
(22) (23) (24)
五、计算题(第23、24题,每题5分.第25、26题每题6分,共22分)
23.如图,AB∥CD∥PN,∠ABC=50°,∠CPN=150°.求∠BCP的度数.
【提示】由AB∥CD,∠ABC=50°可得∠BCD=50°.
由PN∥CD,∠CPN=150°,可得∠PCD=30°.
∴ ∠BCP=∠BCD-∠PCD=50°-30°=20°.【答案】20°.
24.如图,∠CAB=100°,∠ABF=110°,AC∥PD,BF∥PE,求∠DPE的度数.
【提示】由AC∥PD,∠CAB=100°,可得∠APD=80°.
同理可求∠BPE=70°.
∴ ∠DPE=180°-∠APD-∠BPE=180°-80°-70°=30°.【答案】30°.
25.如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC.
求∠PAG的度数.
(25) (26-1) (26-2)
【提示】由DB∥FG∥EC,可得
∠BAC=∠BAG+∠CAG =∠DBA+∠ACE =60°+36°=96°.
由AP平分∠BAC得∠CAP=∠BAC=×96°=48°.
由FG∥EC得∠GAC=ACE=36°.∴ ∠PAG=48°-36°=12°.【答案】12°.
26.如图,AB∥CD,∠1=115°,∠2=140°,求∠3的度数.
【提示】过点E作EG∥AB.∵ AB∥CD由平行公理推论可得EG∥CD.
由此可求得∠AEC的度数.由平角定义可求得∠3的度数.【答案】75°.
(五)证明题(每题6分,共24分)
27.已知:如图.AB∥CD,∠B=∠C.求证:∠E=∠F.
(27) (28) (29-1)
【提示】证明AC∥BD.【答案】证明:∵ AB∥CD(已知),
∴ ∠B=∠CDF(两直线平行,同位角相等).
∵ ∠B=∠C(已知), ∴ ∠CDF=∠C(等量代换).
∴ AC∥BD(内错角相等,两直线平行).
∴ ∠E=∠F(两直线平行,内错角相等).
28.已知:如图,AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.
【提示】由AC∥DE.DC∥EF证∠1=∠3.由DC∥EF证∠2=∠4.再由CD平分∠BCA,即可证得∠3=∠4.
【答案】证明:∵ AC∥DE(已知),∴ ∠1=∠5(两直线平行,内错角相等).
同理∠5=∠3. ∴ ∠1=∠3(等量代换).
∵ DC∥EF(已知), ∴ ∠2=∠4(两直线平行,同位角相等).
∵ CD平分∠ACB, ∴ ∠1=∠2(角平分线定义),
∴ ∠3=∠4(等量代换), ∴ EF平分∠BED(角平分线定义).
29.已知:如图,AB∥CD,∠1=∠B,∠2=∠D.求证:BE⊥DE.
【提示】过点E作EF∥AB,证明∠BED=90°.
【答案】证明:过点E作EF∥AB.
∴ ∠BEF=∠B(两直线平行,内错角相等).
∵ ∠B=∠1, ∴ ∠BEF=∠1(等量代换).
同理可证:∠DEF=∠2.
∵ ∠1+∠BEF+∠DEF+∠2=180°(平角定义),
即2∠BEF+2∠DEF=180°,
∴ ∠BEF+∠DEF=90°(等式性质).
即∠BED=90°. ∴ BE⊥DE(垂直的定义).
30.已知:如图,AB∥CD,请你观察∠E、∠B、∠D之间有什么关系,并证明你所得的结论.
【提示】结论:∠B+∠E=∠D.过点E作EF∥AB.
【答案】结论:∠B+∠E=∠D.
证明:过点E作EF∥AB,
∴ ∠FEB=∠B(两直线平行,内错角相等).
∵ AB∥CD,EF∥AB,
∴ EF∥CD(平行公理推论),
∴ ∠FED=∠D(两直线平行,内错角相等).
∵ ∠FED=∠FEB+∠BED=∠B+∠BED,
∴ ∠B+∠BED=∠D(等量代换).
本题还可添加如图所示的辅助线,请你证明∠B+∠E=∠D.
【点评】这是一道探索结论型的问题.要通过对直观图形仔细观察,大胆猜想,设定结论,再进行推理,验证结论.直观图形是观察思考的依据,准确的直观图形可引发正确的直觉思维.所以作图不可忽视.直觉思维是正确,还必须用相关的理论来验证.这样得到的结论方可靠.
能 力 检 测 二
1.如果两个角的一边在同一直线上,另一边互相平行,那么这两个角的关系是( ).
A.相等 B.互补 C.相等或互补 D.相等且互补
2.已知∠AOB=30°,自∠AOB的顶点O引射线OC,若∠AOC : ∠AOB=4 : 3 ,则∠BOC等于( ).
A.10° B. 40° C.70° D. 10°或70°
3.一个角等于它的补角的5倍,那么这个角的补角的余角是( ).
A.30° B.60° C.45° D.以上答案都不对
4.用一副三角板可以作出大于0°而小于180°的角的个数( ).
A. 5个 B.10个 C. 11个 D.以上都不对
5.已知三条直线a,b,c,下列命题中错误的是( )
A.如果a∥b,b∥c,那么a∥c
B.如果a⊥b,b⊥c,那么a⊥c
C.如果a⊥b,b⊥c,那么a∥c
D.如果a⊥b,a∥c,那么b⊥c
6.如果两条平行线被第三条直线所截得的8个角中,有一个角的度数已知,
则( ).
A.只能求出其余3个角的度数 B.能求出其余5个角的度数
C.只能求出其余6个角的度数 D. 能求出其余7个角的度数
7.若两条平行线被第三条直线所截,则下列说法错误的是( ).
A.一对同位角的平分线互相平行
B.一对内错角的平分线互相平行
C.一对同旁内角的平分线互相垂直
D.一对同旁内角的平分线互相平行
8.下列说法,其中正确的是( ).
A.两条直线被第三条直线所截,内错角相等;
B.不相交的两条直线就是平行线;
C.点到直线的垂线段,叫做点到直线的距离;
D.同位角相等,两直线平行.
9.下列关于对顶角的说法:
(1)相等的角是对顶角 (2)对顶角相等
(3)不相等的角不是对顶角 (4)不是对顶角不相等
其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
10.如果∠α与∠β是邻补角,且∠α> ∠β,那么∠β的余角是( ).
A.(∠α±∠β) B. ∠α
C. (∠α-∠β) D.不能确定
二、填空题(本题共 4 小题,每小题 5 分,满分 20 分)
11.如果两个角的两边分别平行且一个角比另一个角的3倍少30°,则这两个角的度数分别
为_________.
12.如图1,已知∠AOC=∠BOD=78°,∠BOC=30°,则∠AOD的度数是_________.
13.如图2,三条直线两两相交,图中共有_________对对顶角,共有_________对同位角,共有_________对内错角,共有_________对同旁内角.
14.如图3,AB∥CD,直线l平分∠AOE,∠1 = 40°,则∠2 = _________.
图1 图2 图3
三、(本题共2小题,每小题8分,满分 16 分)
15.如图,∠1=∠2,∠1+∠2=162°,求∠3与∠4的度数.
16.如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系,为什么?
四、(本题共2小题,每小题8分,满分16分)
17.已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.求证:∠P= .
18.如图,OM、ON分别是∠BOC和∠AOC的平分线,且∠AOB=84°.
(1)求∠MON的度数
(2)当OC在∠AOB内转动时,∠MON的值是否会变,简单说明理由.
五、(本题共2小题,每小题10分,满分20分)
19.如图,已知DE∥BC,CD是∠ACB的平分线,∠B=70°,∠ACB=50°,求∠EDC和∠BDC的度数.
20.如图,∠1=∠2,能判断AB∥DF吗?若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由.
六、(本题满分12 分)
21.如图,左图是一个三角形,已知∠ACB=90°,小明用三角尺在这个三角形中画了一条高CD(点D是垂足),得到右图 :
(1)请你帮小明画出这条高;
(2)在右图中,小明通过仔细观察、认真思考,找出了三对余角,你能帮小明把它们写出来吗?
(3)∠ACB、∠ADC、∠CDB都是直角,所以∠ACB =∠ADC=∠CDB,小明还发现了另外两对相等的角,请你也仔细地观察、认真地思考分析,试一试,能发现吗?把它们写出来,并请说明理由.
七、(本题满分12分)
22.如图,AB∥CD,求∠BAE+∠AEF+∠EFC+∠FCD的度数.
八、(本题满分14 分)
23.如图, 已知:AF、BD、CE、ABC、DEF均是直线,∠EQF=∠APB,
∠C=∠D.求证:∠A=∠F.
参考答案
一、1、C 2、D 3、B 4、C 5、B 6、D 7、D 8、D
9、B 10、C .
二、11、15°与15°或52 .5°与127.5°; 12、126°; 13、6,12,6;
14、70°.
三、15、54°,72°;16、CD∥AB.提示:∠EFB+∠FBA=180°.
四、17、∵AB∥CD,∴∠BEF+∠DFE=180°
又∵∠BEF的平分线与∠DFE的平分线相交于点P,∴∠PEF=∠BEF,∠PFE=∠DEF
∴∠PEF+∠PFE=(∠BEF+∠DFE)=90°
∵∠PEF+∠PFE+∠P=180° ∴∠P=90°.
18、(1)42°,(2)∠MON=∠AOB;
五、19、25°,85°;
20、不能,添加∠CBD=∠EDB,∵∠1=∠2,∴∠ABD=∠FDB,∴AB∥DF.
六、21、(1)略;(2)∠ACD与∠A,∠DCB与∠B,∠A与∠B;(3)∠ACD=∠B,∠DCB=∠A,同角的余角相等.
所以这个等边圆柱的表面积为2r2+2r·2r=24(cm2).)
七、22、540°提示:过E、F点分别作与AB平行的直线.
八、23、∵∠EQF=∠APB,∠EQF=∠AQC.
∴∠APB=∠AQC.
∴BD∥EC.
∴∠ABD=∠C.
又∵∠C=∠D,∴∠ABD=∠D
∴AC∥DF.
∴∠A=∠F.
典型例题:
例1:(2008辽宁)如图1,直线,分别与相交,如果,那么的度数是( )
A. B. C. D.
例2:(2006河南)两条直线相交所成的四个角中,下列说法正确的是( )
A.一定有一个锐角B.一定有一个钝角 C.一定有一个直角 D.一定有一个不是钝角
例3:(2008资阳)如图,CA⊥BE于A,AD⊥BF于D,下列说法正确的是( )
A.α的余角只有∠B B.α的邻补角是∠DAC
C.∠ACF是α的余角 D.α与∠ACF互补
例4:(2007河池)一副三角板,如图2叠放在一起,∠的度数是 度.
例5:(2008永州)一个角的补角是这个角的余角的3倍,则这个角为度 .
例6:(2007北京)如图,已知△ABC.
(1)请你在BC边上分别取两点D,E(BC的中点除外),连结AD,AE,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;
(2)请你根据使(1)成立的相应条件,证明AB+AC>AD+AE.
实战演练:
1.(2007南宁)如图,直线被直线所截,若,,
则 .
2.(2008永州)如图,直线a、b被直线c所截,若要a∥b,需增加条件 (填一个即可).
3.(2008山西)如右图,直线a∥b,直线AC分别交a、b于点B、C,直线AD交a于点D.若∠1=20 o, ∠2=65 o,则∠3= .
4.(2006南宁)如图,已知相交于点,,,
则 度.
5.(2008仙桃)如图是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(下底挖去一小半圆),刀片上、下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2= 度.
6.(2008资阳)如图,CA⊥BE于A,AD⊥BF于D,下列说法正确的是( )
A.α的余角只有∠B B.α的邻补角是∠DAC
C.∠ACF是α的余角 D.α与∠ACF互补
7.(2008孝感)如图,分别在上,为两平行线间一点,那么( )
A. B. C. D.
8.(2008荆州)将一直角三角板与两边平行的纸条如图
所示放置,下列结论:(1)∠1=∠2;(2)∠3=∠4;
(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确
的个数 是( )
A.1 B.2 C.3 D.4
9.(2007黄冈)下列各图中,∠1大于∠2的是( )
10.(2008杭州)设一个锐角与这个角的补角的差的绝对值为,则( )
A. 0°<<90° B. 0°<≤90°
C. 0°<<90°或90°<<180° D. 0°<<180°
11.(2006河南)如图,线段AB=4,点O是线段AB上的点,点C、D是线段OA、OB的中点,小明很轻松地求得CD=2.他在反思过程中突发奇想:若点O运动到线段AB的延长线上或直线AB外,原有的结论“CD=2”是仍然成立呢?请帮小明画出图形分析,并说明理由.
应用探究:
1.(2008连云港)已知为矩形的对角线,则图中与一定不相等的是( )
A. B. C. D.
2.(2007十堰)一条公路两次转弯后又回到原来的方向(即,
如图).如果第一次转弯时的,那么,应是( )
A. B.
C. D.
3.(2008烟台)如图,小明从A 处出发沿北偏东60°向行走至B处,又沿北偏西20°方向行走至 C 处,此时需把方向调整到与出发时一致,则方向的调整应是( )
A.右转80° B.左传80° C.右转100° D.左传100°
4.(2007绍兴)学行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4) ):
从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等; ②两直线平行,内错角相等;
③同位角相等,两直线平行; ④内错角相等,两直线平行.
A.①② B.②③ C.③④ D.①④
5.(2007福州)如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立(直接回答成立或不成立)?
(3)当动点P落在第③部分时,全面探究∠PAC、∠APB、∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
参考答案
典型例题:
例1:C 例2:D 例3:D 例4:105 例5:45°
例6:解:(1)如图1,;
(2)证法一:如图2,分别过点D,B作CA,EA的平行线,两线交于F点,DF与AB交于G点.
所以,.
在和中,又CE=BD,
可证.
所以AC=FD,AE=FB.
在中,AG+DG>AD,
在中,BG+FG>FB,
所以AG+DG-AD>0,BG+FG-FB>0.
所以AG+DG+BG+FG-AD-FB>0.
即AB+FD>AD+FB.
所以AB+AC>AD+AE.
证法二:如图3,分别过点A,E作CB,CA,的平行线,两线交于F点,EF与AB交于G点,连结BF.
则四边形EFCA是平行四边形.
所以FE=AC,AF=CE.
因为BD=CE,
所以BD=AF.
所以四边形是平行四边形.
所以FB=AD.
在中,AG+EG>AE,
在中,BG+FG>FB,
可推得AG+EG+BG+FG>AE+FB.
所以AB+AC>AD+AE.
证法三:如图4,取DE的中点O,连结AO并延长到F点,使得FO=AO,连结EF,CF.在和中,又,DO=EO.
可证.
所以AD=FE.
因为BD=CE,DO=EO,
所以BO=CO.
同理可证.
所以AB=FC.
延长AE交CF于G点.
在中,AC+CG>AE+EG,
在中,EG+FG>EF.
可推得AC+CG+EG+FG>AE+EG+EF.
即AC+CF>AE+EF.
所以AB+AC>AD+AE.
实战演练:
1. 60 2.或或 3.45 o
4.62 5.90 6.D 7.C 8.D 9.C 10.D
应用探究:
1.D 2.A 3.A 4.D
5. (1)解法一:如图9-1
延长BP交直线AC于点E
∵ AC∥BD , ∴ ∠PEA = ∠PBD .
∵ ∠APB = ∠PAE + ∠PEA ,
∴ ∠APB = ∠PAC + ∠PBD .
解法二:如图9-2
过点P作FP∥AC ,
∴ ∠PAC = ∠APF .
∵ AC∥BD , ∴FP∥BD .
∴ ∠FPB =∠PBD .
∴ ∠APB =∠APF +∠FPB =∠PAC + ∠PBD .
解法三:如图9-3,
∵ AC∥BD , ∴ ∠CAB +∠ABD = 180°
即 ∠PAC +∠PAB +∠PBA +∠PBD = 180°.
又∠APB +∠PBA +∠PAB = 180°,
∴ ∠APB =∠PAC +∠PBD .
(2)不成立.
(3)(a)当动点P在射线BA的右侧时,结论是
∠PBD=∠PAC+∠APB .
(b)当动点P在射线BA上,
结论是∠PBD =∠PAC +∠APB .
或∠PAC =∠PBD +∠APB 或 ∠APB = 0°,
∠PAC =∠PBD(任写一个即可).
(c) 当动点P在射线BA的左侧时,
结论是∠PAC =∠APB +∠PBD .
选择(a) 证明:
如图9-4,连接PA,连接PB交AC于M
∵ AC∥BD ,
∴ ∠PMC =∠PBD .
又∵∠PMC =∠PAM +∠APM ,
∴ ∠PBD =∠PAC +∠APB .
选择(b) 证明:如图9-5
∵ 点P在射线BA上,∴∠APB = 0°.
∵ AC∥BD , ∴∠PBD =∠PAC .
∴ ∠PBD =∠PAC +∠APB
或∠PAC =∠PBD+∠APB
或∠APB = 0°,∠PAC =∠PBD.
选择(c) 证明:
如图9-6,连接PA,连接PB交AC于F
∵ AC∥BD , ∴∠PFA =∠PBD .
∵ ∠PAC =∠APF +∠PFA ,
∴ ∠PAC =∠APB +∠PBD .
能 力 检 测 题 三
一、选择题(每小题4分,共20分)
下面四个图形中,∠1与∠2是对顶角的图形的个数是( )
A.0 B.1 C.2 D.3
一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐50°,第二次左拐130° B.第一次左拐50°,第二次右拐50°
C.第一次左拐50°,第二次左拐130° D.第一次右拐50°,第二次右拐50°
如图,若m∥n,∠1 = 105°,则∠2 =( )
A.55° B.60° C.65° D.75°
同一平面内的四条直线满足,则下列式子成立的是( )
A. B. C. D.
在5×5方格纸中将图(1)中的图形N平移后的位置如图(2)中所示,那么正确的平移方法是( ).
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
二、填空题 (每空3分,共24分)
如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD = 38°,则∠AOC = ,∠COB =
下面生活中的物体的运动情况可以看成平移的是 。(填序号)
动的钟摆 (2)在笔直的公路上行驶的汽车 (3)随风摆动的旗帜 ⑷汽车玻璃上雨刷的运动(5)从楼顶自由落下的球(球不旋转)。
将“对顶角相等”改写成“如果…,那么…”的形式是_______________________________________.
如图,EF∥AD,∠1 =∠2,∠BAC = 70°。将求∠AGD的过程填写完整。因为EF∥AD,所以 ∠2 = 。又因为 ∠1 = ∠2,所以 ∠1 = ∠3。 所以AB∥ 。所以∠BAC + = 180°。又因为∠BAC = 70°,所以∠AGD = 。
三、解答题(共56分)
填空并在括号内加注理由。(每空1分,共10分)
如图4,已知DE∥BC,DF、BE分别平分∠ADE和∠ABC
求证:∠FDE=∠DEB
证明:∵DE∥BC
∴∠ADE= ( )
∵DF、BE平分∠ADE、∠ABC
∴∠ADF=
∴∠ABE= ( )
∴∠ADF=∠ABE
∴ ∥ ( )
∴∠FDE=∠ ( )
如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外。如何测量(运用本章知识)?(本题6分)
(本题10分)在方格中平移△ABC,
使点A移到点M, 使点A移到点N
② 分别画出两次平移后的三角形
(本题10分)已知:如图,AB∥CD,∠B=400,∠E=300,求∠D的度数
(本题10分)如图,已知DE∥BC,∠1=∠2,求证:∠B=∠C.
(本题10分)已知:如图∠1=∠2,∠C=∠D,∠A=∠F相等吗?试说明理由.
答案:
1-5 BBDCC
6.52° 128°
7.⑵⑸
8.如果两个角是对顶角,那么这两个角相等.
9.∠3 DG ∠AGD 110°.
10.∠ABC两直线平行,同位角相等.∠ADE ∠ABC 角平分线的定义. DF、BE同位角相等,两直线平行.DEB两直线平行,内错角相等.
11.反向延长OA到C,测量出BOC的度数为n°则∠AOB的度数为(180-n)°(邻补角互补).
12.略.
13. 70°.
14.∵DE∥BC ∴∠1=∠B ∠2=∠C(两直线平行,同位角相等)又∠1=∠2 ∴∠B=∠C(等量代换).
15.∠A=∠F.∵∠1=∠DGF(对顶角相等)又∠1=∠2 ∴∠DGF=∠2 ∴DB∥EC(同位角相等,两直线平行) ∴∠DBA=∠C(两直线平行,同位角相等) 又∵∠C=∠D ∴∠DBA=∠D ∴DF∥AC(内错角相等,两直线平行)∴∠A=∠F(两直线平行,内错角相等).
A
O
C
B
D
A
B
C
D
E
l
l1
l2
1
2
1
2
c
a
b
E
B
D
A
O
C
a
b
M
P
N
1
2
3
1
2
3
4
5
B
A
1
D
C
2
1
1
2
B
A
D
C
B
A
C
1
2
D
1
2
B
A
D
C
A
B
①
②
③
④
A
B
①
②
③
④
A
B
①
②
③
④
P
(第5题图)
C
D
C
D
C
D
图2
图3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 1 页)
一.基本知识:
1.相交线 2.邻补角 对顶角 3.垂线
4.同位角 内错角 同旁内角的定义 6.平行的定义
7.平行线的判定 性质 8.命题与定理的定义 9.平移
(一)..两直线的位置关系:相交(垂直) 平行
(二).各类角的概念及性质
1.同位角 内错角 同旁内角的定义
2.邻补角和对顶角的性质
(1)邻补角互补
(2)对顶角相等
注:“同”指两角位于第三直线的同侧,“错”指两角位于第三直线两侧
“内”指两角位于两被截直线之间
(三).垂线 点到直线的距离
1.垂线的概念:两条直线相交,若其所形成的四个角中有一个角等于90°,
则称这两条直线互相垂直,其中一条直线叫做另一条直线的
垂线,他们的交点叫做垂足
注:(1)垂直是相交的一种特殊情形
(2)两直线垂直必具备两个要点:A.相交 B.有一个角为直角
2.垂线的性质:
(1)在平面门内,过一点有且只有一条直线与已知直线垂直
(2)连接直线外一点与直线上各点的所有县段中,垂线段最短
(四).平行线
1.平行线的概念:在同一平面内,不相交的两条直线叫做平行线
注:平行的前提是两直线在同一平面内
2.平行公理
(1)经过直线外一点,有且只有一条直线与这条直线平行
(2)如果两条直线都与第三条直线平行,那么着两条直线也互相平行,
即如果a∥b,b∥c,那么a∥c
3.平行线的性质
(1)两条平行直线被第三条直线所截,同位角相等
(2)两条平行直线被第三条直线所截,内错角相等
(3)两条平行直线被第三条直线所截,同旁内角互补
4.平行线的距离:同时垂直于两条平行线,并且夹在平行线间的线段的长度,
叫做这两条平行线间的距离
5.平行线的判定
如果两直线被第三条直线所截:
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
二 .典型例题
例1.如图1所示,直线AB.CD相交于点O,∠AOC=40°,求∠COB.∠BOD
∠AOD的度数?
解:由邻补角的定义可得
∠COB=180°—∠AOC=180°—40°=140°
由对顶角相等可得
∠BOD=∠AOC=40°
∠AOD=∠COB=140°
例2.如图2所示,已知∠AOB于∠BOC互为邻补角,OD平分∠AOB,
OE⊥OD,试问:OE是否平分∠COB?为什么?
点拔:在分析∠BOE和∠COE的关系时,可以利用余角的
性质,通过考虑余角,∠BOD和∠AOD的关系,从
而得出结论
解:OE平分∠COB的理由如下:
∵∠AOD+∠BOD+∠BOE+∠ COE=180°,OE⊥OD
∴∠BOE+∠BOD=90°
∵OD平分∠AOB,
∴∠AOD=∠BOD
∴∠AOD+∠BOE=90°
∴∠BOD+∠COE=90° E B
D
∴∠BOE=∠COE,即OE平分∠COB
C O A
图2
例3.如图3所示BE∥DF,AB⊥BE,CD⊥DF,垂足为点B,D,试说明AB∥CD。
点拔:欲说明AB∥CD,只需说明∠ABD=∠CDG,有已知条件可以说明
解:∵BE∥DF(已知)
∴∠DFG=∠DBE(两直线平行,同位角相等)
又∵AB⊥BE,CD⊥DF(已知) A E C F
∴∠ABE=∠CDF=90°(垂直定义)
∴∠ABE+∠DBE=∠CDF+∠DGF(等式性质)
∴∠ABD=∠CDG
B D G
∴AB∥CD(同位角相等,两直线平行)
三.适时训练
一. 选择题:
1. 如果两个角的一边在同一条直线上,另一边互相平行,那么这两个角( )
A. 相等或互补 B. 互补 C. 相等 D. 相等且互与
2. 如图,,,则( )
A. B. C. D.
A
l1
B
l2
α
C
3. 如图,,则( )
A. B. C. D.
l1
1
α
2 l2
4. 如图,能与构成同旁内角的角有( )
A. 1个 B. 5个 C. 3个 D. 4个
α
5. 如图,已知,等于( )
A. B. C. D.
A B
120°
α
25°
C D
6. 如图,平分,则等于( )
A. B. C. D.
B M C
A N P D
7. 如果两个角的两边分别平行,而其中一个角比另一个角的4倍少,那么这两个角是( )
A. B. 都是
C. 或 D. 以上都不对
8. 如图,下面结论正确的是( )
A. 是同位角
B. 是内错角
C. 是同位角
D. 是内错角
9. 如图,图中同旁内角的对数是( )
A. 2对 B. 3对 C. 4对 D. 5对
10. 如图,能与构成同位角的有( )
A. 1个 B. 2个 C. 3个 D. 4个
α
11. 如图,图中的内错角的对数是( )
A. 2对 B. 3对 C. 4对 D. 5对
12. 下列语句中,是对顶角的语句为( )
A. 两条直线相交所成的角
B. 两条直线相交所成的角,且有一个公共顶点,而没有公共边
C.有公共顶点且方向 相反的两个角
D. 有公共顶点并且相等的两个角
13. 图中,是对顶角的为( )
1 2
A B C D
14. 三条直线相交于一点,所成的对顶角的对数是( )
A. 3 B. 4 C. 5 D. 6
15. 点到直线的距离是指这点到这条直线的( )
A. 垂线段的长度 B. 垂线的长 C. 长度 D. 垂线段
16. 如图,三条直线相交于点O,则( )
A. B. C. D.
1 O 3
2 l1
l2
l3
17. 已知:,则的度数为( )
A. B. C. D. 不同于以上答案
二. 填空题:
1. 如图,图中1和E是______和________被_______所截的_______角;
2和3是_________和_________被___________所截的________角;
1和4是_________和________被________所截的_________角;
BCE和E是被_________所截的_______角。
E
A
1 2
4 3
B D C
2. 如图,1的同旁内角是_________,2的内错角是___________,图中共有______对同位角。
M G
A 4 B
E 3 H
2 1
C F D
N
3. 两个互为邻补角的角平分线___________;两个对顶角的角平分线形成___________。
4. 直线AB与CD互相垂直,垂足为O,P是直线CD上一点,则P到AB的距离是__________。
5. 如图1,直线AB、CD、EF都经过O点,并且已知,则__________,_________,________,______。
A F
C O D
E B
图1
6. 如图,直线AB、CD、EF相交于O,且,,则_______,__________。
C
E
A 2 O B
1
F
D
7. 如图:于D,,则__________。
23
A D B
8. 已知:如图,于D,,则________,______,__________。
C
F
1
A D B
E
9. 判断下列图形中,有没有对顶角,若有请写出哪两个角
1.
4
1 3
2.
1 4 8 7
2 3 5 6
9
12 10
11
2.
1 4 8 7
2 3 5 6
9
12 10
11
3.
1 2
3 4 7
5 6
4.
1
2
4.
1
2
EMBED Word.Picture.8 5.
1 4
2 3
三.解答题
1. 如图,直线AB、CD被EF所截,如果互补,且,那么的度数是多少?
C E
2
3 D
4
1 B
A
F
2. 已知:直线AD、BC交于O点,,求:的度数。
A
B O C
D
3. 已知:如图直线AB与CD交于O点,,求:的度数。
A
4 D
2 1
C 3
B
4. 已知:直线AB、EF相交于O点,于O点,,求
C
E
A O B
F
D
5. 如图,直线AB、CD、EF交于点O,是它的余角的2倍,,
且有,求的度数。
A
D
E O F
C
G B
6. 已知:如图,。求证:。
B
C
D
2 3
1
O A
证明:( )
( )
( )
( )
7. 已知:如图,COD是直线,。求证:A、O、B三点在同一条直线上。
A
C
1
2 O
3
D
B
证明:COD是一条直线( )
___________( )
( )
____________________
_______________( )
四. 证明题:
1. 已知:AB//CD,BD平分,DB平分,求证:DA//BC
2. 已知:如图,AB//CE,,求:的度数。
3. 已知:AB//CD,,求证:
4. 已知:如图,AB//CD,MN截AB、CD于E、F,且EG//FH,求证:
5. 已知:AF、BD、CE都为直线,B在直线AC上,E在直线DF上,且,,求证:。
6. 已知:如图,,求证:
7. 已知:如图,,且B、C、D在一条直线上。
求证:
A E
3
1 2
4
B C D
8. 已知:如图,,DE平分,BF平分,且。
求证:
D F C
A E B
9. 已知:如图,。
求证:
A B
1
E
F
2
C P D
10. 已知:如图,。
求证:
F
E
4
A G 1 B
5
3
6 2
C D
11. 如图,已知:CE=DF,AC=BD,1=2。求证:A=B。
12. 已知:如图,E、F分别是AB和CD上的点,DE、AF分别交BC于G、H,A=D,1=2,求证:B=C。
13. 如图,已知:AB//CD,求证:B+D+BED=(至少用三种方法)
【试题答案】
一. 选择题:
1-5 A C C B C 6-10 C .D DCC 11-17 DBCDACD
二. 填空题:
1. AD、EC、BE、同位角;AD、EC、AC、内错角;AB、CD、AD、内错角;EC、同旁内角。
2. 3和GEF;3和GEF;6
3. 互相垂直,一条直线
4. 线段OP的长度
5. 99,145,46。99
6. 63,117
7. =
8. 60,60,120
9. (1). 是对顶角
(2). 是对顶角。
(3). 是对顶角
( 4). 无 (5.) 无
三.解答题
1.
2.
3.
又
4.
又
5.
6. 已知,垂线性质,已知,垂线定义
7. 已知,180,平角定义,已知,,180,A、O、B三点在一条直线上,平角定义
四.证明题
1. ,BD平分,
BD平分,
2.
3.
又
4.
5. ,
6.
7. 证:
8. 证:平分
平分
9. 证:
又
即
10. 证:
11. 证明:
12. 证明:
即AC与BD互相平分。
13. 证明:
又
14. 证明:(1)连结BD。
(2)延长DE交AB延长线于F。
(3)过点E作EF//AB,
能力测试一
(一)判断题(每题2分,共10分)
1.过线段外一点画线段的中垂线……………………………………………………( )
2.如果两个角互为补角,那么它们的角平分线一定互相垂直……………………( )
3.两条直线不平行,同旁内角不互补………………………………………………( )
4.错误地判断一件事情的语句不叫命题……………………………………………( )
5.如图,AB∥CD,那么∠B+∠F+∠D=∠E+∠G………………………… ( )
(5题) (6题) (7题)
(二)填空题(每小题2分,共18分)
6.如图,当∠1=∠ 时,AB∥DC;当∠D+∠ =180°时,AB∥DC;当
∠B=∠ 时,AB∥CD.
7.如图,AB∥CD,AD∥BC,∠B=60°,∠EDA=50°.则∠CDF= .
8.如图,O是△ABC内一点,OD∥AB,OE∥BC,OF∥AC,∠B=45°,∠C=75°,则
∠DOE= ,∠EOF= ,∠FOD= .
(8题) (10题) (11题)
9.两个角的两边分别平行,其中一个角比另一个角的3倍少20°.则这两个角的度数分别是 .
10.如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,
∠B-∠D=24°,则∠GEF= .
11.如图,AD∥BC,点O在AD上,BO、CO分别平分∠ABC、∠DCB,若
∠A+∠D=m°.则∠BOC=______.
12.有一条直的等宽纸带,按图(1)折叠时,纸带重叠部分中的∠ = 度.
13.把命题“在同一平面内垂直于同一直线的两直线互相平行”写成“如果…那么…”的形式是:如果______________,那么_____________.
图(1) (15题) (16题)
(三)选择题(每小题3分,共21分)
15.如图,已知直线AB与CD相交于点O,OE⊥CD.垂足为O,则图中∠AOE和
∠DOB的关系是( )
(A)同位角 (B)对顶角 (C)互为补角 (D)互为余角
16.如图,CD⊥AB,垂足为D,AC⊥BC,垂足为C.图中线段的长能表示点到直线(或线段)距离的线段有…( )
(A)1条 (B)3条 (C)5条 (D)7条
17.若AO⊥BO,垂足为O,∠AOC︰∠AOB=2︰9,则∠BOC的度数等于……( )
(A)20° (B)70° (C)110° (D)70°或110°
18.下列命题中,真命题是……………………………………………………………( )
(A)同位角相等工 (B)同旁内角相等,两直线平行
(C)同旁内角互补 (D)同一平面内,平行于同一直线的两直线平行
20.如图,AD∥EF∥BC,且EG∥AC.那么图中与∠1相等的角(不包括∠1)的个数是( )
(A)2 (B)4 (C)5 (D)6
21.某人从A点出发向北偏东60°方向速到B点,再从B点出发向南偏西15°方向速到C点,则∠ABC等于…( )
(A)75° (B)105° (C)45° (D)135°
(四)解答题(本题5分)
22.根据命题“角平分线上的点到角的两边距离相等”,画出图形,并结合图形写出已知、求证(不证明).
五、计算题(第23、24题,每题5分.第25、26题每题6分,共22分)
23.如图,AB∥CD∥PN,∠ABC=50°,∠CPN=150°.求∠BCP的度数.
24.如图,∠CAB=100°,∠ABF=110°,AC∥PD,BF∥PE,求∠DPE的度数.
25.如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC.
求∠PAG的度数.
26.如图,AB∥CD,∠1=115°,∠2=140°,求∠3的度数.
(五)证明题(每题6分,共24分)
27.已知:如图.AB∥CD,∠B=∠C.求证:∠E=∠F.
28.已知:如图,AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.
29.已知:如图,AB∥CD,∠1=∠B,∠2=∠D.求证:BE⊥DE.
30.已知:如图,AB∥CD,请你观察∠E、∠B、∠D之间有什么关系,并证明你所得的结论.
参考答案
(一)判断题(每题2分,共10分)
1.过线段外一点画线段的中垂线……………………………………………………( )
【提示】线段外一点不一定在线段的中垂线上,所以过线段外一点画线段的垂线,不一定平分这条线段如图PQ⊥AB,垂足为O.但PQ不平分AB.【答案】×.
(1) (2) (3)
2.如果两个角互为补角,那么它们的角平分线一定互相垂直……………………( )
【提示】两个角互为补角时,这两个角可以是邻补角,也可以不是邻补角.当两角互补但不是邻补角时,则它们的角平分线不互相垂直.如图:∠AOB与∠AOC互补,OM平分∠AOC、ON平分∠AOB.显然OM与ON不垂直.【答案】×.
3.两条直线不平行,同旁内角不互补………………………………………………( )
【提示】如图,AB与CD不平行,EF与AB交于点G.与CD交于点H.
过点G作PQ∥CD.
∴ ∠QGF+∠GHD=180°.
∵ ∠BGF<∠QGF,
∴ ∠BGF+∠GHD<180°;
又 ∠PGH+∠GHC=180°,
∵ ∠AGH>∠PGH,
∴ ∠AGH+∠GHC>180°.
即两直线不平行,同旁内角不互补.【答案】√.
4.错误地判断一件事情的语句不叫命题…( )
【提示】判断一件事情的语句叫做命题.错误地判断得到的是假命题.假命题也是命题.
【答案】×.
5.如图,AB∥CD,那么∠B+∠F+∠D=∠E+∠G…………………………( )
【提示】过点E、F、G分别画EP∥AB,PQ∥AB,GM∥AB.
则AB∥EP∥FQ∥GM∥CD.
∴ ∠B=∠1,∠3=∠2,∠4=∠5,∠D=∠6.
∴ ∠B+∠3+∠4+∠D=∠1+∠2+∠5+∠6.
即∠B+∠EFG+∠D=∠BEF+∠FG(D) 【答案】√.
(二)填空题(每小题2分,共18分)
6.如图,当∠1=∠ 时,AB∥DC;当∠D+∠ =180°时,AB∥DC;当∠B=∠ 时,AB∥CD.
(6) (7) (8)
【提示】把题中的“AB∥CD”视作条件去找∠1的内错角、∠D的同旁内角和∠B的同位角.即得要填的角.【答案】4,DAB,5.
7.如图,AB∥CD,AD∥BC,∠B=60°,∠EDA=50°.则∠CDF= .
【提示】由AB∥CD,得∠DCF=∠B=60°,
由AD∥BC得∠ADC=∠DCF=60°,
∴ ∠ADE+∠ADC=50°+60°=110°,
∴ ∠CDF=180°-110°=70°. 【答案】70°.
8.如图,O是△ABC内一点,OD∥AB,OE∥BC,OF∥AC,∠B=45°,∠C=75°,则∠DOE= ,∠EOF= ,∠FOD= .
【提示】由OD∥AB,∠B=45°,得∠ODC=∠B=45°.
由OE∥DC,∠DOE+∠ODC=180°,∴ ∠DOE=180°-45°=135°.
同理可求∠EOF=105°.由周角的定义可求∠FOD=120°.
【答案】135°,105°,120°.
9.两个角的两边分别平行,其中一个角比另一个角的3倍少20°.则这两个角的度数分别是 .
【提示】如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
设一个角为x度.则另一个角为(3x-20)度.
依据上面的性质得,
3x-20=x,或3x-20+x=180°.
∴ x=10,或x=50.
当x=50时,3x-20=3×50-20=130.
【答案】10°、10°或50°、130°.
【点评】通过列方程(或方程组)解题是几何计算常用的方法.
10.如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,
∠B-∠D=24°,则∠GEF= .
(10) (11)
【提示】由AB∥EF∥CD,可知∠BED=∠B+∠D.
已知∠B+∠BED+∠D=192°.
∴ 2∠B+2∠D=192°,∠B+∠D=96°.
又 ∠B-∠D=24°.
于是可得关于∠B、∠D的方程组解得 ∠B=60°.
由AB∥EF知∠BEF=∠B=60°.因为EG平分∠BEF,所以∠GEF=∠BEF=30°.
【答案】30°.
11.如图,AD∥BC,点O在AD上,BO、CO分别平分∠ABC、∠DCB,若
∠A+∠D=m°.则∠BOC=______.
【提示】由AD∥BC,BO平分∠ABC,可知∠AOB=∠CBO=∠ABC.
同理∠DOC=∠BCO=∠DCB.
∵ AD∥BC,∴ ∠A+∠ABC=180°,∠D+∠DCB=180°,
∴ ∠A+∠D+∠ABC+∠DCB=360°.
∵ ∠A+∠D=m°,∴ ∠ABC+∠DCB=360°-m°.
∴ ∠AOB+∠DOC=(∠ABC+∠DCB)=(360°-m°)=180°-m°.
∴ ∠BOC=180°-(∠AOB+∠DOC)=180°-(180°-m°)=m°.
【答案】m°.
12.有一条直的等宽纸带,按图(1)折叠时,纸带重叠部分中的∠ =度.
【提示】裁一张等宽纸带按图示折叠,体会一下题目的含义.将等宽纸带展平,便得图(2).由此图可知∠DAC=30°.AB是∠C′AC的平分线.∴ ∠ =75°.【答案】75°.
图(2) 图(1)
【点评】解类似具有操作性的实际问题时,不妨动手做一做,从中感受一下题目的意义,进而将实际问题转化成数学问题.用数学知识解决实际问题.这样做不仅能培养我们抽象思维和空间想象能力,而且能提高我们解决实际问题的能力.
13.把命题“在同一平面内垂直于同一直线的两直线互相平行”写成“如果…那么…”的形式是:如果______________,那么_____________.
【答案】在同一平面内两条直线垂直于同一条直线,这两条直线互相平行.
14.如图,在长方体中,与面BCC′B′平行的面是面;与面BCC′B′垂直的面是,与棱A′A平行的面有,与棱A′A垂直的面有.
(15)
【答案】面ADD′A;面ABB′A′,面ABCD,面A′B′C′D′,面DCC′D′;
面DCC′D′,面BCC′B′;面ABCD,面A′B′C′D′.
(三)选择题(每小题3分,共21分)
15.如图,已知直线AB与CD相交于点O,OE⊥CD.垂足为O,则图中∠AOE和
∠DOB的关系是( )(A)同位角 (B)对顶角 (C)互为补角 (D)互为余角
【提示】由OE⊥CD,知:∠AOE与∠AOC互余.∠AOC与∠BOD是对顶角.所以∠AOE与∠DOB互为余角.【答案】D.
16.如图,CD⊥AB,垂足为D,AC⊥BC,垂足为C.图中线段的长能表示点到直线(或线段)距离的线段有…( )(A)1条 (B)3条 (C)5条 (D)7条
【提示】CD的长表示点C到AB的距离;AC的长表示点A到BC的距离;BC的长表示点B到AC的距离;AD的长表示点A到CD的距离,BD的长表示点B到CD的距离.共5条.【答案】C.
17.若AO⊥BO,垂足为O,∠AOC︰∠AOB=2︰9,则∠BOC的度数等于……( )
(A)20° (B)70° (C)110° (D)70°或110°
【提示】OC可在∠AOB内部,也可在∠AOB外部,如图可示,故有两解.
设∠AOC=2x°,则∠AOB=9x°.
∵ AO⊥BO, ∴ ∠AOB=90°.
∵ 9x=90°,x=10°,∠AOC=2x=20°.
(1)∠BOC=∠AOB-∠AOC=90°-20°=70°;
(2)∠BOC=∠AOB+∠AOC=90°+20°=110°.
【答案】D.
18.下列命题中,真命题是……………………………………………………………( )
(A)同位角相等工 (B)同旁内角相等,两直线平行
(C)同旁内角互补 (D)同一平面内,平行于同一直线的两直线平行
【提示】两直线不平行,则同位角不相等,同旁内角不互补,所以A、C错误,B也不一定成立.如图所示直线a、b被直线c所截.∠1=∠2,∠3=∠4.显然a与b不平行.
(18) (20) (21)
【答案】D.
19.直线AB∥CD,且与EF、GH相交成如图可示的图形,则共得同旁内角…( )
(A)4对 (B)8对 (C)12对 (D)16对
【提示】该图可分离出四个基本图形,如图所示.
第三条直线截两平行线,此时图形呈“”型,有同旁内角两对;
第三条直线截两相交线,此时图形呈“”型,有同旁内角六对.
故图中共有同旁内角2×2+6×2=16(对). 【答案】D.
20.如图,AD∥EF∥BC,且EG∥AC.那么图中与∠1相等的角(不包括∠1)的个数是……( )(A)2 (B)4 (C)5 (D)6
【提示】由AD∥EF∥BC,且EG∥AC可得:
∠1=∠DAH=∠FHC=∠HCG=∠EGB=∠GEH除∠1共5个.【答案】C.
21.某人从A点出发向北偏东60°方向速到B点,再从B点出发向南偏西15°方向速到C点,则∠ABC等于……………………………………………………………( )
(A)75° (B)105° (C)45° (D)135°
【提示】按要求画出图形再计算
∵ NA∥BS, ∴ ∠NAB=∠SBA=60°.
∵ ∠SBC=15°, ∴ ∠ABC=∠SBA-∠SBC=60°-15°=45°.【答案】C.
(四)解答题(本题5分)
22.根据命题“角平分线上的点到角的两边距离相等”,画出图形,并结合图形写出已知、求证(不证明).
【答案】已知:OC平分∠AOB,P是OC上任意一点.PD⊥OB,PE⊥OA,垂足分别是D、E.求证:PE=PD.
(22) (23) (24)
五、计算题(第23、24题,每题5分.第25、26题每题6分,共22分)
23.如图,AB∥CD∥PN,∠ABC=50°,∠CPN=150°.求∠BCP的度数.
【提示】由AB∥CD,∠ABC=50°可得∠BCD=50°.
由PN∥CD,∠CPN=150°,可得∠PCD=30°.
∴ ∠BCP=∠BCD-∠PCD=50°-30°=20°.【答案】20°.
24.如图,∠CAB=100°,∠ABF=110°,AC∥PD,BF∥PE,求∠DPE的度数.
【提示】由AC∥PD,∠CAB=100°,可得∠APD=80°.
同理可求∠BPE=70°.
∴ ∠DPE=180°-∠APD-∠BPE=180°-80°-70°=30°.【答案】30°.
25.如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC.
求∠PAG的度数.
(25) (26-1) (26-2)
【提示】由DB∥FG∥EC,可得
∠BAC=∠BAG+∠CAG =∠DBA+∠ACE =60°+36°=96°.
由AP平分∠BAC得∠CAP=∠BAC=×96°=48°.
由FG∥EC得∠GAC=ACE=36°.∴ ∠PAG=48°-36°=12°.【答案】12°.
26.如图,AB∥CD,∠1=115°,∠2=140°,求∠3的度数.
【提示】过点E作EG∥AB.∵ AB∥CD由平行公理推论可得EG∥CD.
由此可求得∠AEC的度数.由平角定义可求得∠3的度数.【答案】75°.
(五)证明题(每题6分,共24分)
27.已知:如图.AB∥CD,∠B=∠C.求证:∠E=∠F.
(27) (28) (29-1)
【提示】证明AC∥BD.【答案】证明:∵ AB∥CD(已知),
∴ ∠B=∠CDF(两直线平行,同位角相等).
∵ ∠B=∠C(已知), ∴ ∠CDF=∠C(等量代换).
∴ AC∥BD(内错角相等,两直线平行).
∴ ∠E=∠F(两直线平行,内错角相等).
28.已知:如图,AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.
【提示】由AC∥DE.DC∥EF证∠1=∠3.由DC∥EF证∠2=∠4.再由CD平分∠BCA,即可证得∠3=∠4.
【答案】证明:∵ AC∥DE(已知),∴ ∠1=∠5(两直线平行,内错角相等).
同理∠5=∠3. ∴ ∠1=∠3(等量代换).
∵ DC∥EF(已知), ∴ ∠2=∠4(两直线平行,同位角相等).
∵ CD平分∠ACB, ∴ ∠1=∠2(角平分线定义),
∴ ∠3=∠4(等量代换), ∴ EF平分∠BED(角平分线定义).
29.已知:如图,AB∥CD,∠1=∠B,∠2=∠D.求证:BE⊥DE.
【提示】过点E作EF∥AB,证明∠BED=90°.
【答案】证明:过点E作EF∥AB.
∴ ∠BEF=∠B(两直线平行,内错角相等).
∵ ∠B=∠1, ∴ ∠BEF=∠1(等量代换).
同理可证:∠DEF=∠2.
∵ ∠1+∠BEF+∠DEF+∠2=180°(平角定义),
即2∠BEF+2∠DEF=180°,
∴ ∠BEF+∠DEF=90°(等式性质).
即∠BED=90°. ∴ BE⊥DE(垂直的定义).
30.已知:如图,AB∥CD,请你观察∠E、∠B、∠D之间有什么关系,并证明你所得的结论.
【提示】结论:∠B+∠E=∠D.过点E作EF∥AB.
【答案】结论:∠B+∠E=∠D.
证明:过点E作EF∥AB,
∴ ∠FEB=∠B(两直线平行,内错角相等).
∵ AB∥CD,EF∥AB,
∴ EF∥CD(平行公理推论),
∴ ∠FED=∠D(两直线平行,内错角相等).
∵ ∠FED=∠FEB+∠BED=∠B+∠BED,
∴ ∠B+∠BED=∠D(等量代换).
本题还可添加如图所示的辅助线,请你证明∠B+∠E=∠D.
【点评】这是一道探索结论型的问题.要通过对直观图形仔细观察,大胆猜想,设定结论,再进行推理,验证结论.直观图形是观察思考的依据,准确的直观图形可引发正确的直觉思维.所以作图不可忽视.直觉思维是正确,还必须用相关的理论来验证.这样得到的结论方可靠.
能 力 检 测 二
1.如果两个角的一边在同一直线上,另一边互相平行,那么这两个角的关系是( ).
A.相等 B.互补 C.相等或互补 D.相等且互补
2.已知∠AOB=30°,自∠AOB的顶点O引射线OC,若∠AOC : ∠AOB=4 : 3 ,则∠BOC等于( ).
A.10° B. 40° C.70° D. 10°或70°
3.一个角等于它的补角的5倍,那么这个角的补角的余角是( ).
A.30° B.60° C.45° D.以上答案都不对
4.用一副三角板可以作出大于0°而小于180°的角的个数( ).
A. 5个 B.10个 C. 11个 D.以上都不对
5.已知三条直线a,b,c,下列命题中错误的是( )
A.如果a∥b,b∥c,那么a∥c
B.如果a⊥b,b⊥c,那么a⊥c
C.如果a⊥b,b⊥c,那么a∥c
D.如果a⊥b,a∥c,那么b⊥c
6.如果两条平行线被第三条直线所截得的8个角中,有一个角的度数已知,
则( ).
A.只能求出其余3个角的度数 B.能求出其余5个角的度数
C.只能求出其余6个角的度数 D. 能求出其余7个角的度数
7.若两条平行线被第三条直线所截,则下列说法错误的是( ).
A.一对同位角的平分线互相平行
B.一对内错角的平分线互相平行
C.一对同旁内角的平分线互相垂直
D.一对同旁内角的平分线互相平行
8.下列说法,其中正确的是( ).
A.两条直线被第三条直线所截,内错角相等;
B.不相交的两条直线就是平行线;
C.点到直线的垂线段,叫做点到直线的距离;
D.同位角相等,两直线平行.
9.下列关于对顶角的说法:
(1)相等的角是对顶角 (2)对顶角相等
(3)不相等的角不是对顶角 (4)不是对顶角不相等
其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
10.如果∠α与∠β是邻补角,且∠α> ∠β,那么∠β的余角是( ).
A.(∠α±∠β) B. ∠α
C. (∠α-∠β) D.不能确定
二、填空题(本题共 4 小题,每小题 5 分,满分 20 分)
11.如果两个角的两边分别平行且一个角比另一个角的3倍少30°,则这两个角的度数分别
为_________.
12.如图1,已知∠AOC=∠BOD=78°,∠BOC=30°,则∠AOD的度数是_________.
13.如图2,三条直线两两相交,图中共有_________对对顶角,共有_________对同位角,共有_________对内错角,共有_________对同旁内角.
14.如图3,AB∥CD,直线l平分∠AOE,∠1 = 40°,则∠2 = _________.
图1 图2 图3
三、(本题共2小题,每小题8分,满分 16 分)
15.如图,∠1=∠2,∠1+∠2=162°,求∠3与∠4的度数.
16.如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系,为什么?
四、(本题共2小题,每小题8分,满分16分)
17.已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.求证:∠P= .
18.如图,OM、ON分别是∠BOC和∠AOC的平分线,且∠AOB=84°.
(1)求∠MON的度数
(2)当OC在∠AOB内转动时,∠MON的值是否会变,简单说明理由.
五、(本题共2小题,每小题10分,满分20分)
19.如图,已知DE∥BC,CD是∠ACB的平分线,∠B=70°,∠ACB=50°,求∠EDC和∠BDC的度数.
20.如图,∠1=∠2,能判断AB∥DF吗?若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由.
六、(本题满分12 分)
21.如图,左图是一个三角形,已知∠ACB=90°,小明用三角尺在这个三角形中画了一条高CD(点D是垂足),得到右图 :
(1)请你帮小明画出这条高;
(2)在右图中,小明通过仔细观察、认真思考,找出了三对余角,你能帮小明把它们写出来吗?
(3)∠ACB、∠ADC、∠CDB都是直角,所以∠ACB =∠ADC=∠CDB,小明还发现了另外两对相等的角,请你也仔细地观察、认真地思考分析,试一试,能发现吗?把它们写出来,并请说明理由.
七、(本题满分12分)
22.如图,AB∥CD,求∠BAE+∠AEF+∠EFC+∠FCD的度数.
八、(本题满分14 分)
23.如图, 已知:AF、BD、CE、ABC、DEF均是直线,∠EQF=∠APB,
∠C=∠D.求证:∠A=∠F.
参考答案
一、1、C 2、D 3、B 4、C 5、B 6、D 7、D 8、D
9、B 10、C .
二、11、15°与15°或52 .5°与127.5°; 12、126°; 13、6,12,6;
14、70°.
三、15、54°,72°;16、CD∥AB.提示:∠EFB+∠FBA=180°.
四、17、∵AB∥CD,∴∠BEF+∠DFE=180°
又∵∠BEF的平分线与∠DFE的平分线相交于点P,∴∠PEF=∠BEF,∠PFE=∠DEF
∴∠PEF+∠PFE=(∠BEF+∠DFE)=90°
∵∠PEF+∠PFE+∠P=180° ∴∠P=90°.
18、(1)42°,(2)∠MON=∠AOB;
五、19、25°,85°;
20、不能,添加∠CBD=∠EDB,∵∠1=∠2,∴∠ABD=∠FDB,∴AB∥DF.
六、21、(1)略;(2)∠ACD与∠A,∠DCB与∠B,∠A与∠B;(3)∠ACD=∠B,∠DCB=∠A,同角的余角相等.
所以这个等边圆柱的表面积为2r2+2r·2r=24(cm2).)
七、22、540°提示:过E、F点分别作与AB平行的直线.
八、23、∵∠EQF=∠APB,∠EQF=∠AQC.
∴∠APB=∠AQC.
∴BD∥EC.
∴∠ABD=∠C.
又∵∠C=∠D,∴∠ABD=∠D
∴AC∥DF.
∴∠A=∠F.
典型例题:
例1:(2008辽宁)如图1,直线,分别与相交,如果,那么的度数是( )
A. B. C. D.
例2:(2006河南)两条直线相交所成的四个角中,下列说法正确的是( )
A.一定有一个锐角B.一定有一个钝角 C.一定有一个直角 D.一定有一个不是钝角
例3:(2008资阳)如图,CA⊥BE于A,AD⊥BF于D,下列说法正确的是( )
A.α的余角只有∠B B.α的邻补角是∠DAC
C.∠ACF是α的余角 D.α与∠ACF互补
例4:(2007河池)一副三角板,如图2叠放在一起,∠的度数是 度.
例5:(2008永州)一个角的补角是这个角的余角的3倍,则这个角为度 .
例6:(2007北京)如图,已知△ABC.
(1)请你在BC边上分别取两点D,E(BC的中点除外),连结AD,AE,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;
(2)请你根据使(1)成立的相应条件,证明AB+AC>AD+AE.
实战演练:
1.(2007南宁)如图,直线被直线所截,若,,
则 .
2.(2008永州)如图,直线a、b被直线c所截,若要a∥b,需增加条件 (填一个即可).
3.(2008山西)如右图,直线a∥b,直线AC分别交a、b于点B、C,直线AD交a于点D.若∠1=20 o, ∠2=65 o,则∠3= .
4.(2006南宁)如图,已知相交于点,,,
则 度.
5.(2008仙桃)如图是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(下底挖去一小半圆),刀片上、下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2= 度.
6.(2008资阳)如图,CA⊥BE于A,AD⊥BF于D,下列说法正确的是( )
A.α的余角只有∠B B.α的邻补角是∠DAC
C.∠ACF是α的余角 D.α与∠ACF互补
7.(2008孝感)如图,分别在上,为两平行线间一点,那么( )
A. B. C. D.
8.(2008荆州)将一直角三角板与两边平行的纸条如图
所示放置,下列结论:(1)∠1=∠2;(2)∠3=∠4;
(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确
的个数 是( )
A.1 B.2 C.3 D.4
9.(2007黄冈)下列各图中,∠1大于∠2的是( )
10.(2008杭州)设一个锐角与这个角的补角的差的绝对值为,则( )
A. 0°<<90° B. 0°<≤90°
C. 0°<<90°或90°<<180° D. 0°<<180°
11.(2006河南)如图,线段AB=4,点O是线段AB上的点,点C、D是线段OA、OB的中点,小明很轻松地求得CD=2.他在反思过程中突发奇想:若点O运动到线段AB的延长线上或直线AB外,原有的结论“CD=2”是仍然成立呢?请帮小明画出图形分析,并说明理由.
应用探究:
1.(2008连云港)已知为矩形的对角线,则图中与一定不相等的是( )
A. B. C. D.
2.(2007十堰)一条公路两次转弯后又回到原来的方向(即,
如图).如果第一次转弯时的,那么,应是( )
A. B.
C. D.
3.(2008烟台)如图,小明从A 处出发沿北偏东60°向行走至B处,又沿北偏西20°方向行走至 C 处,此时需把方向调整到与出发时一致,则方向的调整应是( )
A.右转80° B.左传80° C.右转100° D.左传100°
4.(2007绍兴)学行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4) ):
从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等; ②两直线平行,内错角相等;
③同位角相等,两直线平行; ④内错角相等,两直线平行.
A.①② B.②③ C.③④ D.①④
5.(2007福州)如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立(直接回答成立或不成立)?
(3)当动点P落在第③部分时,全面探究∠PAC、∠APB、∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
参考答案
典型例题:
例1:C 例2:D 例3:D 例4:105 例5:45°
例6:解:(1)如图1,;
(2)证法一:如图2,分别过点D,B作CA,EA的平行线,两线交于F点,DF与AB交于G点.
所以,.
在和中,又CE=BD,
可证.
所以AC=FD,AE=FB.
在中,AG+DG>AD,
在中,BG+FG>FB,
所以AG+DG-AD>0,BG+FG-FB>0.
所以AG+DG+BG+FG-AD-FB>0.
即AB+FD>AD+FB.
所以AB+AC>AD+AE.
证法二:如图3,分别过点A,E作CB,CA,的平行线,两线交于F点,EF与AB交于G点,连结BF.
则四边形EFCA是平行四边形.
所以FE=AC,AF=CE.
因为BD=CE,
所以BD=AF.
所以四边形是平行四边形.
所以FB=AD.
在中,AG+EG>AE,
在中,BG+FG>FB,
可推得AG+EG+BG+FG>AE+FB.
所以AB+AC>AD+AE.
证法三:如图4,取DE的中点O,连结AO并延长到F点,使得FO=AO,连结EF,CF.在和中,又,DO=EO.
可证.
所以AD=FE.
因为BD=CE,DO=EO,
所以BO=CO.
同理可证.
所以AB=FC.
延长AE交CF于G点.
在中,AC+CG>AE+EG,
在中,EG+FG>EF.
可推得AC+CG+EG+FG>AE+EG+EF.
即AC+CF>AE+EF.
所以AB+AC>AD+AE.
实战演练:
1. 60 2.或或 3.45 o
4.62 5.90 6.D 7.C 8.D 9.C 10.D
应用探究:
1.D 2.A 3.A 4.D
5. (1)解法一:如图9-1
延长BP交直线AC于点E
∵ AC∥BD , ∴ ∠PEA = ∠PBD .
∵ ∠APB = ∠PAE + ∠PEA ,
∴ ∠APB = ∠PAC + ∠PBD .
解法二:如图9-2
过点P作FP∥AC ,
∴ ∠PAC = ∠APF .
∵ AC∥BD , ∴FP∥BD .
∴ ∠FPB =∠PBD .
∴ ∠APB =∠APF +∠FPB =∠PAC + ∠PBD .
解法三:如图9-3,
∵ AC∥BD , ∴ ∠CAB +∠ABD = 180°
即 ∠PAC +∠PAB +∠PBA +∠PBD = 180°.
又∠APB +∠PBA +∠PAB = 180°,
∴ ∠APB =∠PAC +∠PBD .
(2)不成立.
(3)(a)当动点P在射线BA的右侧时,结论是
∠PBD=∠PAC+∠APB .
(b)当动点P在射线BA上,
结论是∠PBD =∠PAC +∠APB .
或∠PAC =∠PBD +∠APB 或 ∠APB = 0°,
∠PAC =∠PBD(任写一个即可).
(c) 当动点P在射线BA的左侧时,
结论是∠PAC =∠APB +∠PBD .
选择(a) 证明:
如图9-4,连接PA,连接PB交AC于M
∵ AC∥BD ,
∴ ∠PMC =∠PBD .
又∵∠PMC =∠PAM +∠APM ,
∴ ∠PBD =∠PAC +∠APB .
选择(b) 证明:如图9-5
∵ 点P在射线BA上,∴∠APB = 0°.
∵ AC∥BD , ∴∠PBD =∠PAC .
∴ ∠PBD =∠PAC +∠APB
或∠PAC =∠PBD+∠APB
或∠APB = 0°,∠PAC =∠PBD.
选择(c) 证明:
如图9-6,连接PA,连接PB交AC于F
∵ AC∥BD , ∴∠PFA =∠PBD .
∵ ∠PAC =∠APF +∠PFA ,
∴ ∠PAC =∠APB +∠PBD .
能 力 检 测 题 三
一、选择题(每小题4分,共20分)
下面四个图形中,∠1与∠2是对顶角的图形的个数是( )
A.0 B.1 C.2 D.3
一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐50°,第二次左拐130° B.第一次左拐50°,第二次右拐50°
C.第一次左拐50°,第二次左拐130° D.第一次右拐50°,第二次右拐50°
如图,若m∥n,∠1 = 105°,则∠2 =( )
A.55° B.60° C.65° D.75°
同一平面内的四条直线满足,则下列式子成立的是( )
A. B. C. D.
在5×5方格纸中将图(1)中的图形N平移后的位置如图(2)中所示,那么正确的平移方法是( ).
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
二、填空题 (每空3分,共24分)
如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD = 38°,则∠AOC = ,∠COB =
下面生活中的物体的运动情况可以看成平移的是 。(填序号)
动的钟摆 (2)在笔直的公路上行驶的汽车 (3)随风摆动的旗帜 ⑷汽车玻璃上雨刷的运动(5)从楼顶自由落下的球(球不旋转)。
将“对顶角相等”改写成“如果…,那么…”的形式是_______________________________________.
如图,EF∥AD,∠1 =∠2,∠BAC = 70°。将求∠AGD的过程填写完整。因为EF∥AD,所以 ∠2 = 。又因为 ∠1 = ∠2,所以 ∠1 = ∠3。 所以AB∥ 。所以∠BAC + = 180°。又因为∠BAC = 70°,所以∠AGD = 。
三、解答题(共56分)
填空并在括号内加注理由。(每空1分,共10分)
如图4,已知DE∥BC,DF、BE分别平分∠ADE和∠ABC
求证:∠FDE=∠DEB
证明:∵DE∥BC
∴∠ADE= ( )
∵DF、BE平分∠ADE、∠ABC
∴∠ADF=
∴∠ABE= ( )
∴∠ADF=∠ABE
∴ ∥ ( )
∴∠FDE=∠ ( )
如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外。如何测量(运用本章知识)?(本题6分)
(本题10分)在方格中平移△ABC,
使点A移到点M, 使点A移到点N
② 分别画出两次平移后的三角形
(本题10分)已知:如图,AB∥CD,∠B=400,∠E=300,求∠D的度数
(本题10分)如图,已知DE∥BC,∠1=∠2,求证:∠B=∠C.
(本题10分)已知:如图∠1=∠2,∠C=∠D,∠A=∠F相等吗?试说明理由.
答案:
1-5 BBDCC
6.52° 128°
7.⑵⑸
8.如果两个角是对顶角,那么这两个角相等.
9.∠3 DG ∠AGD 110°.
10.∠ABC两直线平行,同位角相等.∠ADE ∠ABC 角平分线的定义. DF、BE同位角相等,两直线平行.DEB两直线平行,内错角相等.
11.反向延长OA到C,测量出BOC的度数为n°则∠AOB的度数为(180-n)°(邻补角互补).
12.略.
13. 70°.
14.∵DE∥BC ∴∠1=∠B ∠2=∠C(两直线平行,同位角相等)又∠1=∠2 ∴∠B=∠C(等量代换).
15.∠A=∠F.∵∠1=∠DGF(对顶角相等)又∠1=∠2 ∴∠DGF=∠2 ∴DB∥EC(同位角相等,两直线平行) ∴∠DBA=∠C(两直线平行,同位角相等) 又∵∠C=∠D ∴∠DBA=∠D ∴DF∥AC(内错角相等,两直线平行)∴∠A=∠F(两直线平行,内错角相等).
A
O
C
B
D
A
B
C
D
E
l
l1
l2
1
2
1
2
c
a
b
E
B
D
A
O
C
a
b
M
P
N
1
2
3
1
2
3
4
5
B
A
1
D
C
2
1
1
2
B
A
D
C
B
A
C
1
2
D
1
2
B
A
D
C
A
B
①
②
③
④
A
B
①
②
③
④
A
B
①
②
③
④
P
(第5题图)
C
D
C
D
C
D
图2
图3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 1 页)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
