人教版八年级数学上册:12.3 角的平分线的性质 教案
文档属性
| 名称 | 人教版八年级数学上册:12.3 角的平分线的性质 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 59.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 11:47:22 | ||
图片预览

文档简介
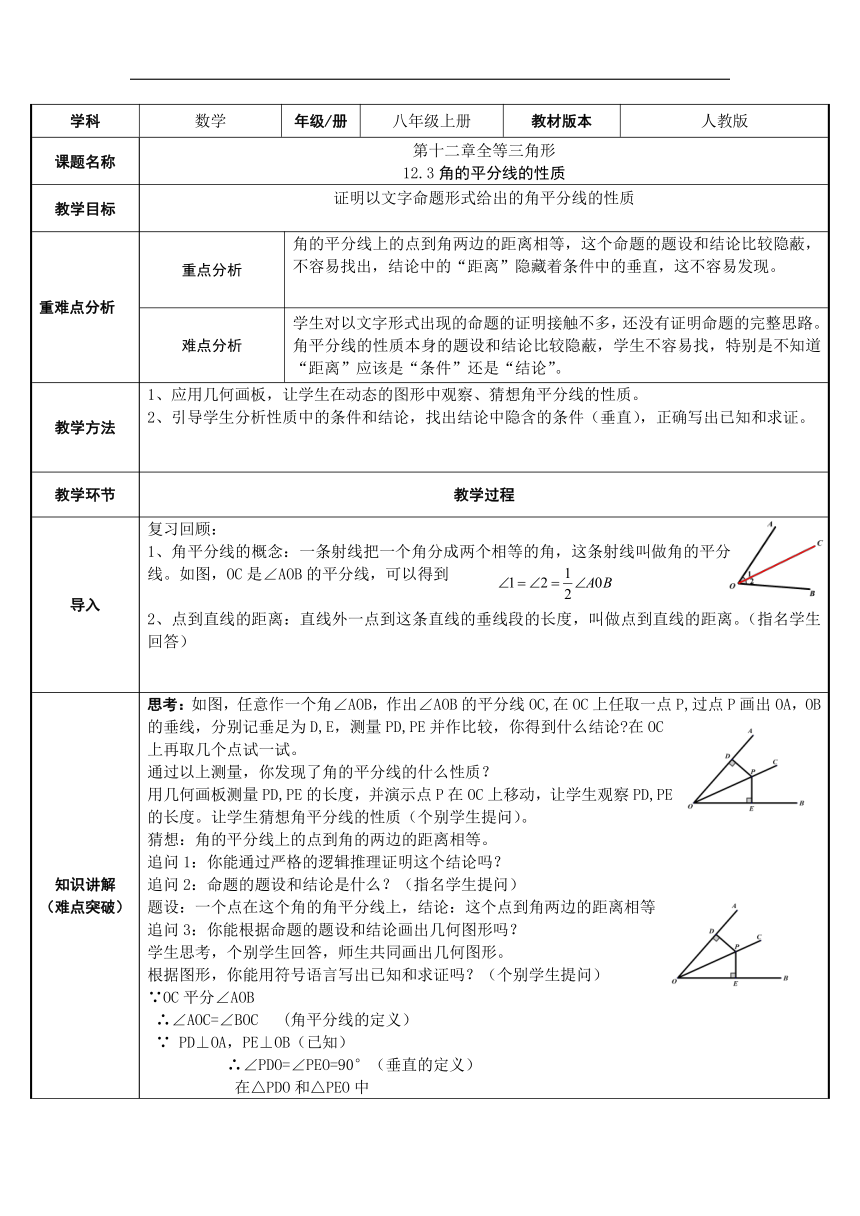
学科
数学
年级/册
八年级上册
教材版本
人教版
课题名称
第十二章全等三角形
12.3角的平分线的性质
教学目标
证明以文字命题形式给出的角平分线的性质
重难点分析
重点分析
角的平分线上的点到角两边的距离相等,这个命题的题设和结论比较隐蔽,不容易找出,结论中的“距离”隐藏着条件中的垂直,这不容易发现。
难点分析
学生对以文字形式出现的命题的证明接触不多,还没有证明命题的完整思路。角平分线的性质本身的题设和结论比较隐蔽,学生不容易找,特别是不知道“距离”应该是“条件”还是“结论”。
教学方法
应用几何画板,让学生在动态的图形中观察、猜想角平分线的性质。
引导学生分析性质中的条件和结论,找出结论中隐含的条件(垂直),正确写出已知和求证。
教学环节
教学过程
导入
复习回顾:
1、角平分线的概念:一条射线把一个角分成两个相等的角,这条射线叫做角的平分线。如图,OC是∠AOB的平分线,可以得到
2、点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。(指名学生回答)
知识讲解
(难点突破)
思考:如图,任意作一个角∠AOB,作出∠AOB的平分线OC,在OC上任取一点P,过点P画出OA,OB的垂线,分别记垂足为D,E,测量PD,PE并作比较,你得到什么结论?在OC上再取几个点试一试。
通过以上测量,你发现了角的平分线的什么性质?
用几何画板测量PD,PE的长度,并演示点P在OC上移动,让学生观察PD,PE的长度。让学生猜想角平分线的性质(个别学生提问)。
猜想:角的平分线上的点到角的两边的距离相等。
追问1:你能通过严格的逻辑推理证明这个结论吗?
追问2:命题的题设和结论是什么?(指名学生提问)
题设:一个点在这个角的角平分线上,结论:这个点到角两边的距离相等
追问3:你能根据命题的题设和结论画出几何图形吗?
学生思考,个别学生回答,师生共同画出几何图形。
根据图形,你能用符号语言写出已知和求证吗?(个别学生提问)
∵OC平分∠AOB
∴∠AOC=∠BOC
(角平分线的定义)
∵
PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90°(垂直的定义)
在△PDO和△PEO中
∠
AOC=
∠
BOC
∠
PDO=
∠
PEO
OP=OP
∴
△
PDO≌
△
PEO(AAS)
∴
PD=PE(全等三角形的对应边相等)
角平分线的性质:角的平分线上的点到角两边的距离相等。
用符号语言表示为:
∵
OC平分∠AOB,
PD
⊥OA
,PE
⊥OB
∴
PD=PE(角的平分线上的点到角的两边的距离相等)
强调:在应用角平分线的性质是,角平分线和垂直两个条件缺一不可。
性质的作用:用于判断和证明两条线段相等。
课堂练习
(难点巩固)
1、判断题
(1)如图1,OC平分∠AOB,点P在OC上,D,E分别为OA,OB上的点,则DP=EP.(
)
(2)如图2,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E,则DP=EP.(
)
(3)图3,OC平分∠AOB,点P在OC上,PD⊥OA,垂足分别为D,若DP=3,则点P到OB的距离是3
.(
)
2、已知:如图,在△ABC中,AD是它的角平分线,且
BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
小结
角平分线的性质:角的平分线上的点到角的两边的距离相等。
符号语言:
∵
OC是∠AOB的平分线,
又
PD⊥OA,PE⊥OB
∴
PD=PE
(角的平分线上的点到角的两边距离相等).
2、性质的作用:用于判断和证明两条线段相等。
数学
年级/册
八年级上册
教材版本
人教版
课题名称
第十二章全等三角形
12.3角的平分线的性质
教学目标
证明以文字命题形式给出的角平分线的性质
重难点分析
重点分析
角的平分线上的点到角两边的距离相等,这个命题的题设和结论比较隐蔽,不容易找出,结论中的“距离”隐藏着条件中的垂直,这不容易发现。
难点分析
学生对以文字形式出现的命题的证明接触不多,还没有证明命题的完整思路。角平分线的性质本身的题设和结论比较隐蔽,学生不容易找,特别是不知道“距离”应该是“条件”还是“结论”。
教学方法
应用几何画板,让学生在动态的图形中观察、猜想角平分线的性质。
引导学生分析性质中的条件和结论,找出结论中隐含的条件(垂直),正确写出已知和求证。
教学环节
教学过程
导入
复习回顾:
1、角平分线的概念:一条射线把一个角分成两个相等的角,这条射线叫做角的平分线。如图,OC是∠AOB的平分线,可以得到
2、点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。(指名学生回答)
知识讲解
(难点突破)
思考:如图,任意作一个角∠AOB,作出∠AOB的平分线OC,在OC上任取一点P,过点P画出OA,OB的垂线,分别记垂足为D,E,测量PD,PE并作比较,你得到什么结论?在OC上再取几个点试一试。
通过以上测量,你发现了角的平分线的什么性质?
用几何画板测量PD,PE的长度,并演示点P在OC上移动,让学生观察PD,PE的长度。让学生猜想角平分线的性质(个别学生提问)。
猜想:角的平分线上的点到角的两边的距离相等。
追问1:你能通过严格的逻辑推理证明这个结论吗?
追问2:命题的题设和结论是什么?(指名学生提问)
题设:一个点在这个角的角平分线上,结论:这个点到角两边的距离相等
追问3:你能根据命题的题设和结论画出几何图形吗?
学生思考,个别学生回答,师生共同画出几何图形。
根据图形,你能用符号语言写出已知和求证吗?(个别学生提问)
∵OC平分∠AOB
∴∠AOC=∠BOC
(角平分线的定义)
∵
PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90°(垂直的定义)
在△PDO和△PEO中
∠
AOC=
∠
BOC
∠
PDO=
∠
PEO
OP=OP
∴
△
PDO≌
△
PEO(AAS)
∴
PD=PE(全等三角形的对应边相等)
角平分线的性质:角的平分线上的点到角两边的距离相等。
用符号语言表示为:
∵
OC平分∠AOB,
PD
⊥OA
,PE
⊥OB
∴
PD=PE(角的平分线上的点到角的两边的距离相等)
强调:在应用角平分线的性质是,角平分线和垂直两个条件缺一不可。
性质的作用:用于判断和证明两条线段相等。
课堂练习
(难点巩固)
1、判断题
(1)如图1,OC平分∠AOB,点P在OC上,D,E分别为OA,OB上的点,则DP=EP.(
)
(2)如图2,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E,则DP=EP.(
)
(3)图3,OC平分∠AOB,点P在OC上,PD⊥OA,垂足分别为D,若DP=3,则点P到OB的距离是3
.(
)
2、已知:如图,在△ABC中,AD是它的角平分线,且
BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
小结
角平分线的性质:角的平分线上的点到角的两边的距离相等。
符号语言:
∵
OC是∠AOB的平分线,
又
PD⊥OA,PE⊥OB
∴
PD=PE
(角的平分线上的点到角的两边距离相等).
2、性质的作用:用于判断和证明两条线段相等。
