2020-2021学年苏科版八年级数学上册3.3 勾股定理的简单应用同步练习(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级数学上册3.3 勾股定理的简单应用同步练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 346.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 09:46:03 | ||
图片预览


文档简介
第3章
勾股定理第4课时
勾股定理的简单应用
一、选择题(共6小题;共36分)
1.
如图,为求出湖两岸
,
两点之间的距离,一个观测者在点
处设桩,使
恰好为直角三角形,且
.若测得
,,则
,
两点之间的距离为
A.
B.
C.
D.
2.
要从电线杆上离地面
处向地面拉一根长
的电缆,则地面上电缆的固定点与电线杆底部的距离应为
A.
B.
C.
D.
3.
小明要用铁杆制作一个直角三角形天线,要求最短边的长为
,最长边的长为
,则小明需要铁杆的总长度为
A.
B.
C.
D.
4.
如图,一个长、宽、高分别为
,,
的长方体盒子能容下的木棒最长为
A.
B.
C.
D.
5.
一架
长的梯子斜靠在一面竖直的墙上,这时梯脚距离墙边
.如果梯子的顶端沿墙面下滑了
,那么梯脚移动的距离是
A.
B.
C.
D.
6.
如图,一艘轮船以
海里/时的速度从港口
出发向东北方向航行,同时另一艘轮船以
海里/时的速度从港口
出发向东南方向航行,离开港口
小时后,两船相距
A.
海里
B.
海里
C.
海里
D.
海里
二、填空题(共7小题;共42分)
7.
从勾股定理的简单应用中可以发现直角三角形与等腰三角形之间的密切联系,有时把研究等腰三角形转化为研究
?
三角形,这是研究问题的一种策略.
8.
从运用勾股定理解决简单实际问题的过程中,我们进一步认识到把直角三角形中三边关系“”看成一个方程,只要根据问题的条件把它转化为我们会解的方程,就把解实际问题转化为解
?
问题.
9.
如图,在一次冰雪灾害中,一棵树在离地面
处被折断,树的顶端落在离树干底部
处,那么这棵树折断之前的高度是
?
.
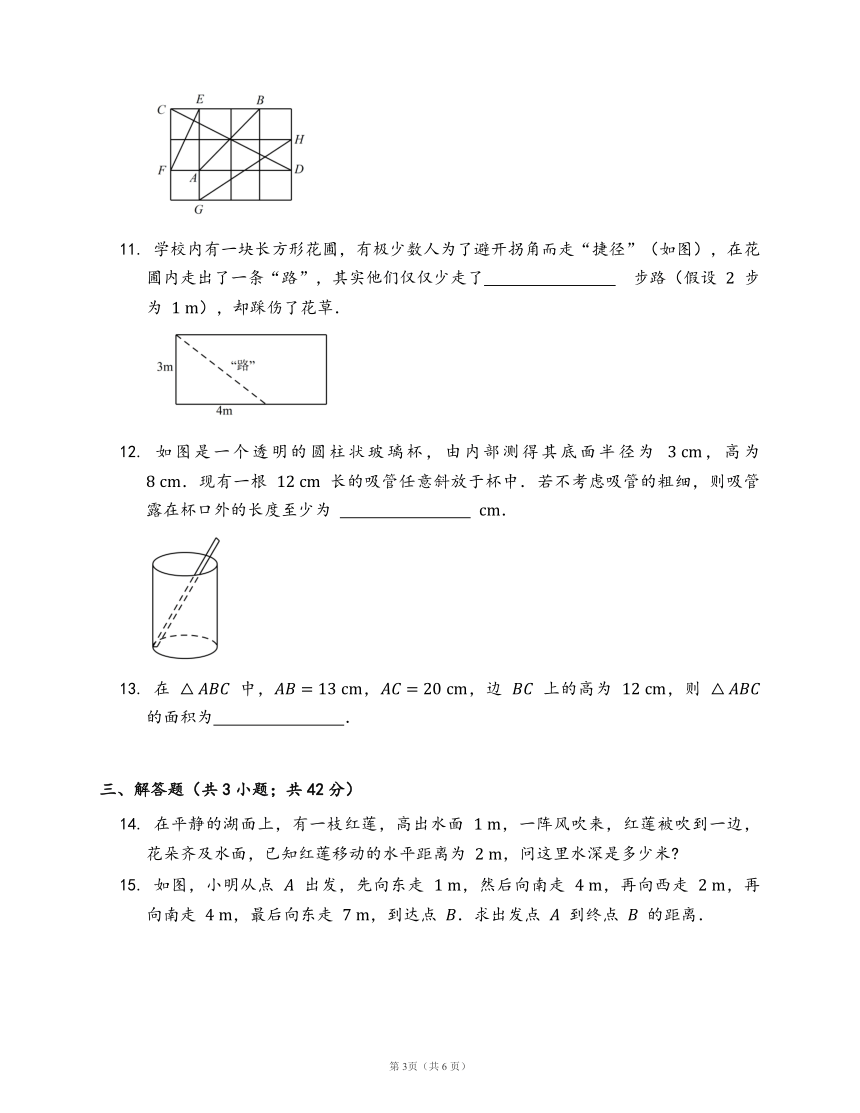
10.
如图,网格中每个小方格的边长均为
,网格中标有
,,,
四条线段,其中,能构成一个直角三角形的三条线段是
?.
11.
学校内有一块长方形花圃,有极少数人为了避开拐角而走“捷径”(如图),在花圃内走出了一条“路”,其实他们仅仅少走了
?
步路(假设
步为
),却踩伤了花草.
12.
如图是一个透明的圆柱状玻璃杯,由内部测得其底面半径为
,高为
.现有一根
长的吸管任意斜放于杯中.若不考虑吸管的粗细,则吸管露在杯口外的长度至少为
?
.
13.
在
中,,,边
上的高为
,则
的面积为
?.
三、解答题(共3小题;共42分)
14.
在平静的湖面上,有一枝红莲,高出水面
,一阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为
,问这里水深是多少米?
15.
如图,小明从点
出发,先向东走
,然后向南走
,再向西走
,再向南走
,最后向东走
,到达点
.求出发点
到终点
的距离.
16.
如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆
处,发现此时绳子末端距离地面
,求旗杆的高度(滑轮上方的绳子忽略不计).
答案
第一部分
1.
D
2.
B
3.
B
4.
C
5.
C
6.
C
第二部分
7.
直角
8.
数学
9.
10.
,,
11.
12.
13.
或
第三部分
14.
如图,
是红莲高出水面的部分,
即
,
是红莲入泥处(根部).
设
,则
,
所以
.
在
中,
根据勾股定理,得
,
即
,
解得
.
所以这里水深是
.
15.
.
点拨:构造直角三角形,由题意,可得两直角边长分别为
,.
由勾股定理得斜边长为
,
即出发点
到终点
的距离.
16.
过点
作
于点
.
设旗杆的高度为
,则
,,,
在
中,
,即
,解得
,
旗杆的高度为
.
第1页(共6
页)
勾股定理第4课时
勾股定理的简单应用
一、选择题(共6小题;共36分)
1.
如图,为求出湖两岸
,
两点之间的距离,一个观测者在点
处设桩,使
恰好为直角三角形,且
.若测得
,,则
,
两点之间的距离为
A.
B.
C.
D.
2.
要从电线杆上离地面
处向地面拉一根长
的电缆,则地面上电缆的固定点与电线杆底部的距离应为
A.
B.
C.
D.
3.
小明要用铁杆制作一个直角三角形天线,要求最短边的长为
,最长边的长为
,则小明需要铁杆的总长度为
A.
B.
C.
D.
4.
如图,一个长、宽、高分别为
,,
的长方体盒子能容下的木棒最长为
A.
B.
C.
D.
5.
一架
长的梯子斜靠在一面竖直的墙上,这时梯脚距离墙边
.如果梯子的顶端沿墙面下滑了
,那么梯脚移动的距离是
A.
B.
C.
D.
6.
如图,一艘轮船以
海里/时的速度从港口
出发向东北方向航行,同时另一艘轮船以
海里/时的速度从港口
出发向东南方向航行,离开港口
小时后,两船相距
A.
海里
B.
海里
C.
海里
D.
海里
二、填空题(共7小题;共42分)
7.
从勾股定理的简单应用中可以发现直角三角形与等腰三角形之间的密切联系,有时把研究等腰三角形转化为研究
?
三角形,这是研究问题的一种策略.
8.
从运用勾股定理解决简单实际问题的过程中,我们进一步认识到把直角三角形中三边关系“”看成一个方程,只要根据问题的条件把它转化为我们会解的方程,就把解实际问题转化为解
?
问题.
9.
如图,在一次冰雪灾害中,一棵树在离地面
处被折断,树的顶端落在离树干底部
处,那么这棵树折断之前的高度是
?
.
10.
如图,网格中每个小方格的边长均为
,网格中标有
,,,
四条线段,其中,能构成一个直角三角形的三条线段是
?.
11.
学校内有一块长方形花圃,有极少数人为了避开拐角而走“捷径”(如图),在花圃内走出了一条“路”,其实他们仅仅少走了
?
步路(假设
步为
),却踩伤了花草.
12.
如图是一个透明的圆柱状玻璃杯,由内部测得其底面半径为
,高为
.现有一根
长的吸管任意斜放于杯中.若不考虑吸管的粗细,则吸管露在杯口外的长度至少为
?
.
13.
在
中,,,边
上的高为
,则
的面积为
?.
三、解答题(共3小题;共42分)
14.
在平静的湖面上,有一枝红莲,高出水面
,一阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为
,问这里水深是多少米?
15.
如图,小明从点
出发,先向东走
,然后向南走
,再向西走
,再向南走
,最后向东走
,到达点
.求出发点
到终点
的距离.
16.
如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆
处,发现此时绳子末端距离地面
,求旗杆的高度(滑轮上方的绳子忽略不计).
答案
第一部分
1.
D
2.
B
3.
B
4.
C
5.
C
6.
C
第二部分
7.
直角
8.
数学
9.
10.
,,
11.
12.
13.
或
第三部分
14.
如图,
是红莲高出水面的部分,
即
,
是红莲入泥处(根部).
设
,则
,
所以
.
在
中,
根据勾股定理,得
,
即
,
解得
.
所以这里水深是
.
15.
.
点拨:构造直角三角形,由题意,可得两直角边长分别为
,.
由勾股定理得斜边长为
,
即出发点
到终点
的距离.
16.
过点
作
于点
.
设旗杆的高度为
,则
,,,
在
中,
,即
,解得
,
旗杆的高度为
.
第1页(共6
页)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
