鲁教版六年级数学上册2.7有理数的乘法课件
文档属性
| 名称 | 鲁教版六年级数学上册2.7有理数的乘法课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 173.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-08 00:00:00 | ||
图片预览








文档简介
(共42张PPT)
第二章 有理数及其运算
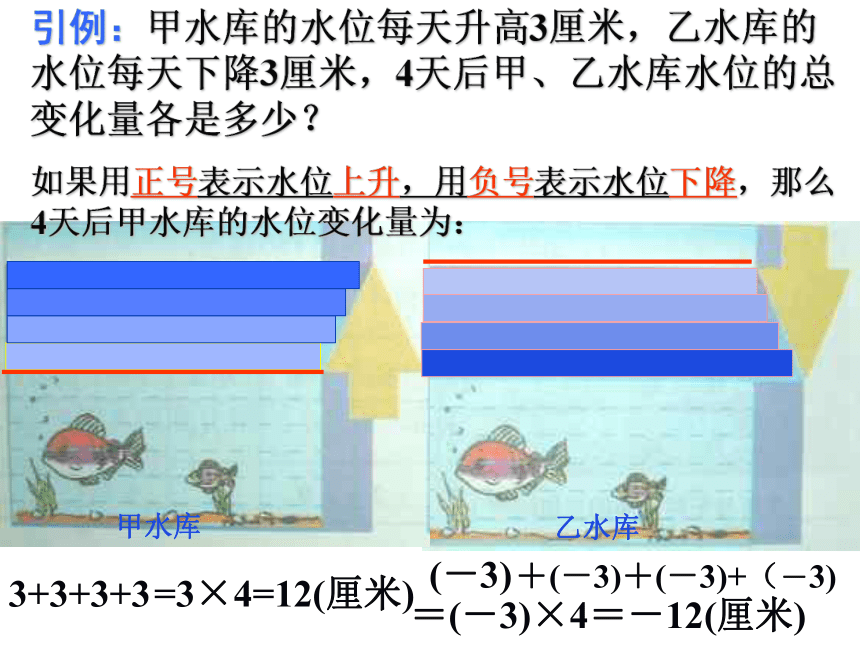
乙水库
甲水库
引例:甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后甲、乙水库水位的总变化量各是多少?
如果用正号表示水位上升,用负号表示水位下降,那么4天后甲水库的水位变化量为:
3+3+3+3
=3×4=12(厘米)
(-3)
+(-3)+(-3)+(-3)
=(-3)×4=-12(厘米)
有理数乘法的类型:
1、正数×正数
2、负数×负数
3、正数×负数
4、负数×正数
5、0 ×正数
6、0 ×负数
议一议
一个因数减小1时,积怎样变化?
-9
-6
-3
0
(-3)× =
(-1)
3
-12
(-3)×(-2)=6
(-3)×(-3)=9
(-3)×(-4)=12
你认为两个有理数相乘有哪些规律?
类似地,我们可以得到:
4×(-4)=
4×(-3)=
4×(-2)=
4×(-1)=
(-4)×0=
(-4)×1=
(-4)×2=
(-4)×(-1)=
(-4)×(-2)=
4×(-4)=_-16____
4×(-3)=_-12____
4×(-2)=_-8____
4×(-1)=_-4____
(-4)×0=__0___
(-4)×1=__-4___
(-4)×2=__-8___
(-4)×(-1)=_4____
(-4)×(-2)=_8____
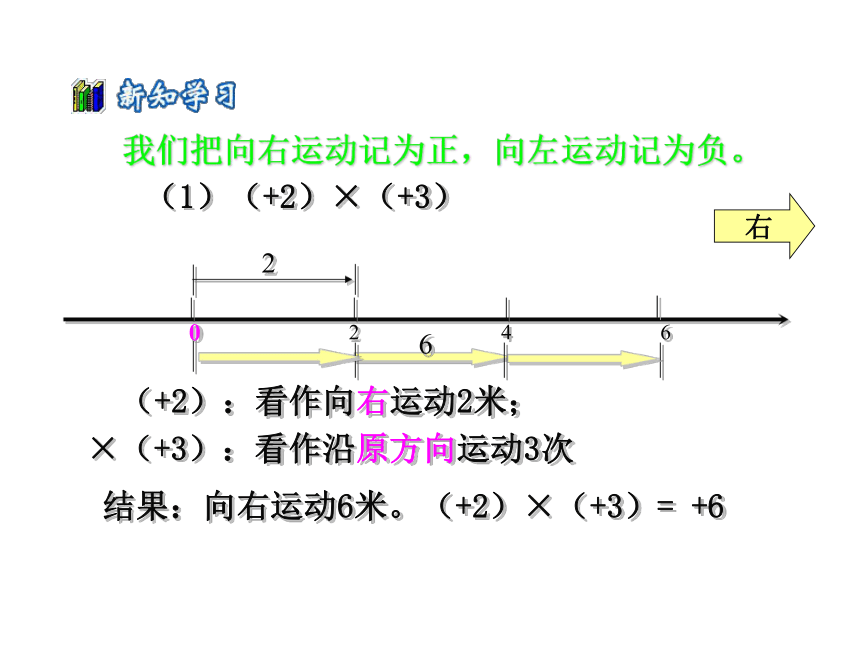
(1)(+2)×(+3)
(+2):看作向右运动2米;
×(+3):看作沿原方向运动3次
结果:向右运动6米。(+2)×(+3)= +6
2
0
2
6
4
6
我们把向右运动记为正,向左运动记为负。
右
-6
-4
0
-2
2
-6
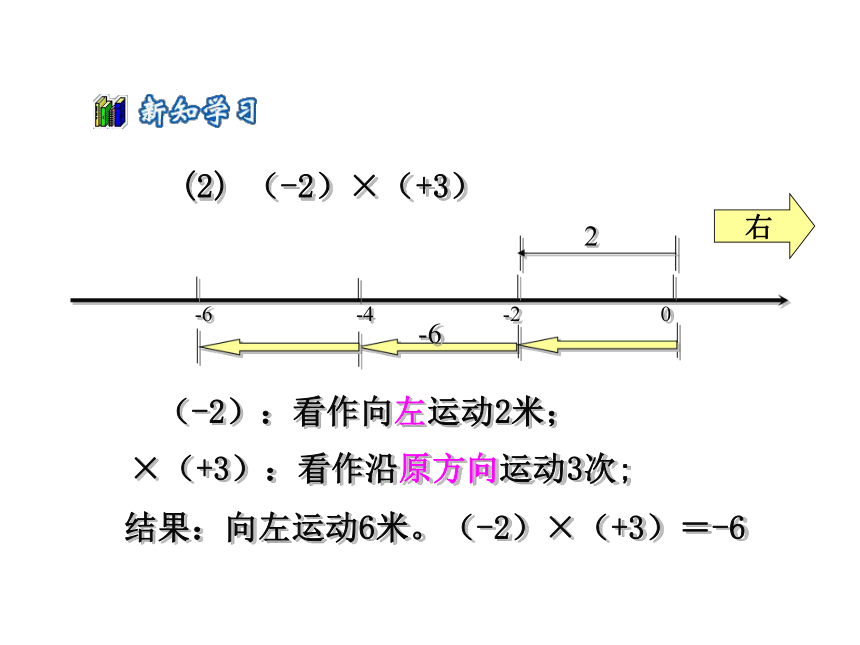
(2) (-2)×(+3)
(-2):看作向左运动2米;
×(+3):看作沿原方向运动3次;
结果:向左运动6米。(-2)×(+3)=-6
右
-6
(3) (+2)×(-3)
(+2):看作向右运动2米;
×(-3):看作沿反方向运动3次。
结果:向左运动6米。(+2)×(-3)= - 6
-6
-4
0
-2
2
右
2
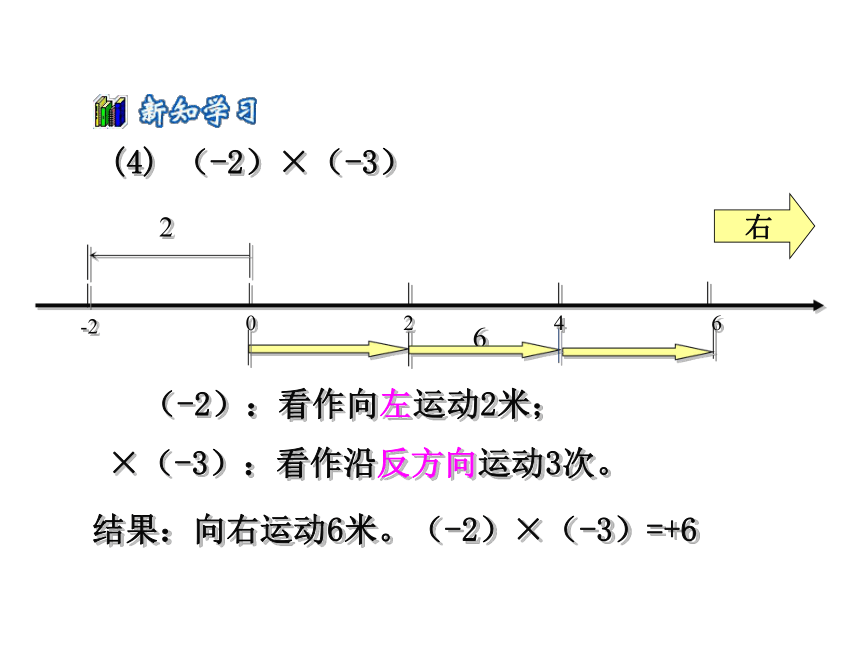
(4) (-2)×(-3)
(-2):看作向左运动2米;
×(-3):看作沿反方向运动3次。
结果:向右运动6米。(-2)×(-3)=+6
2
6
0
2
6
4
-2
右
(5) 0 × 5 = 0
在原地0点运动5次
(-5)× 0 = 0
向原地-5点运动0次
结果:被乘数是0或者乘数是0,结果仍为0。
0 × 0 = 0
(1) 2×3=6
(2)(-2)×(-3)=6
(3)(-2)×3= -6
(4) 2×(-3)= -6
(5)被乘数或乘数为0时,结果是0
5个例子综合如下:
同号相乘 积为正数
异号相乘 积为负数
观察每个式子中的两个因数及积的符号,你能得到什么结论
正乘正得正,
正乘负得负,
负乘正得负,
负乘负得正。
异号得负
同号得正
两数的
符号特征 积的符号 积的绝对值
同 号
异 号
一个数
为0
有理数乘法法则:
+
-
绝对值相乘
绝对值相乘
得 0
先定符号,再定绝对值!
例1: (-7) ×(- 4)
(同号两数乘)
解:(-7)×(- 4)
=
(同号得正)
= + 28
(把绝对值相乘)
例2:(-5)×4×(-0.25)
(从左向右依次运算)
解:原式= 〔(-5)×4〕×(-0.25)
异号得负
绝对值相乘
同号得正
绝对值相乘
=+(20×0.25)
( 7×4 )
+
=〔-(5×4)〕×(-0.25)
=(-20)×(-0.25)
= 5
练习1:先确定下列积的号,然后试计算结果:
(1) 5×(-3)
(2) (-4)×6
(3)(-7)×(-9)
(4) 0.5×0.7
积的符号为负
积的符号为负
积的符号为正
积的符号为正
= -15
= -24
= 63
= 0.35
先确定积的符号,再把绝对值相乘。
练习2、计算(口答):
(1) 6×(-9)=
(2)(-6)×(-9)=
(3)(-6)×9 =
(4) (-6)×1=
(5) ( -6)×(-1) =
(6) 6×(-1) =
-54
54
-54
- 6
6
- 6
练习4、用“<”或“>”号填空:
(1)如果a<0 b>0那么 ab___0
(2)如果a<0 b<0那么 ab___0
练习3、计算:
(1) (-6) ×0.25 (2) (0.5)×(-8)
(- )×(- )
(4) (- )×0
25
6
=-1.5
=-4
=0
>
<
7
10
24
13
=
35
12
练习5、判断下列方程的解是正数、负数还是0:
(1) 4X= -16 (2)-3X=18
(3)-9X=-36 (4)-5X=0
练习6、思考题
(1)当a>0时,a与2a哪个大?
(2)当a<0时,a与2a那个大?
正数
负数
0
负数
2a大
a大
解: (1) (-3) ×(-9) = 27
(2) ( - ) × = -
(3) 7 × (-1) = -7
1
2
1
3
1
6
(-3)×(-9) (2) (- ) ×
7 ×(-1) (4) (-0.8) ×1
⑸(- ) ×(- ) ⑹(-3) ×(- )
1
2
1
3
3
8
8
3
1
3
(-0.8) ×1 = -0.8
⑸(- ) ×(- )=1
3
8
8
3
⑹(-3) ×(- )=1
1
3
观察(3)、(4)两题你有什么发现?能得出什么结论?
观察(5)、(6)两题你有什么发现?能得出什么结论?
练习7、看谁算的又快又对:
注意:
a、一个数同+1相乘,得原数;
一个数同-1相乘,得原数的相反数。
b、乘积为1的两个有理数互为倒数
C、零没有倒数(零作除数无意义)
跟 踪 练 习:
1、说出下列各数的倒数:
(1)-1 (2)-2
2、说出下列各式的结果:
(1) a×(—1)
(2) a× 1
跟 踪 练 习:
1、说出下列各数的倒数:
(1)-1 -1 (2)-2
2、说出下列各式的结果:
(1) a×(—1)
(2) a× 1
1
-
2
-
2
3
5
4
- a
a
3、计算下列各式:
3、计算下列各式:
(1) 5
(2) -1
观察下列各式,它们的积是正的还是负的?
(1) 4×5×0.25=
(2) (-4)×5×0.25=
(3) (-4)×(-5)×0.25=
(4) (-4)×(-5)×(-0.25)=
(5) (-4)×5×(-0.25)×0=
观察下列各式,它们的积是正的 还是负的?
(1) 4×5×0.25= 5
(2) (-4)×5×0.25= -5
(3) (-4)×(-5)×0.25= 5
(4) (-4)×(-5)×(-0.25)= -5
(5) (-4)×5×(-0.25)×0= 0
议一议:
几个有理数相乘,因数都不为0时,积的符号怎样确定?
有一个因数为0时,积是多少?
几个有理数相乘,积的符号由负因数的个数确定:
负因数的个数为偶数个,则积为正数
负因数的个数为奇数个,则积为负数
符号确定后再把绝对值相乘
当有一个因数为零时,积为零。
计算下列各式:
计算下列各式:
-42
7
3
-
5
6
0
1
6
-
4
35
本节课大家学会了什么?
有理数乘法法则如何叙述?
有理数乘法法则的探索采用了什么方法?
小结:
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。
2.如何进行两个有理数的运算:
先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。
注意:
a、一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。
b、乘积为1的两个有理数互为倒数,零没有倒数。
3、乘法法则的探索用到了猜想法和数轴验证法
达 标 检 测
1. 五个有理数的积是负数,则这五个数中负因数的个数是( )
1个 B. 3个 C. 5个 D. 一个或3个或5个
2、 3. 倒数是本身的数有 个,它们是 。
3、 计算(1)(-6) (-2 )=
(2)
(3)
4、下列说法正确的是( )
A、同号两数相乘,取原来的符号 B、两个数相乘,积大于任何一个乘数 C、一个数与0相乘仍得这个数 D、一个数与-1相乘,积为该数的相反数
达 标 检 测
1. 五个有理数的积是负数,则这五个数中负因数的个数是( D )
1个 B. 3个 C. 5个 D. 1个或3个或5个
2、 倒数是本身的数有 2 个,它们是 ±1 。
3、 计算(1)(-6) (-2 )= 14
(2) 5
(3) -1
4、下列说法正确的是(D )
A、同号两数相乘,取原来的符号 B、两个数相乘,积大于任何一个乘数 C、一个数与0相乘仍得这个数 D、一个数与-1相乘,积为该数的相反数
第二章 有理数及其运算
乙水库
甲水库
引例:甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后甲、乙水库水位的总变化量各是多少?
如果用正号表示水位上升,用负号表示水位下降,那么4天后甲水库的水位变化量为:
3+3+3+3
=3×4=12(厘米)
(-3)
+(-3)+(-3)+(-3)
=(-3)×4=-12(厘米)
有理数乘法的类型:
1、正数×正数
2、负数×负数
3、正数×负数
4、负数×正数
5、0 ×正数
6、0 ×负数
议一议
一个因数减小1时,积怎样变化?
-9
-6
-3
0
(-3)× =
(-1)
3
-12
(-3)×(-2)=6
(-3)×(-3)=9
(-3)×(-4)=12
你认为两个有理数相乘有哪些规律?
类似地,我们可以得到:
4×(-4)=
4×(-3)=
4×(-2)=
4×(-1)=
(-4)×0=
(-4)×1=
(-4)×2=
(-4)×(-1)=
(-4)×(-2)=
4×(-4)=_-16____
4×(-3)=_-12____
4×(-2)=_-8____
4×(-1)=_-4____
(-4)×0=__0___
(-4)×1=__-4___
(-4)×2=__-8___
(-4)×(-1)=_4____
(-4)×(-2)=_8____
(1)(+2)×(+3)
(+2):看作向右运动2米;
×(+3):看作沿原方向运动3次
结果:向右运动6米。(+2)×(+3)= +6
2
0
2
6
4
6
我们把向右运动记为正,向左运动记为负。
右
-6
-4
0
-2
2
-6
(2) (-2)×(+3)
(-2):看作向左运动2米;
×(+3):看作沿原方向运动3次;
结果:向左运动6米。(-2)×(+3)=-6
右
-6
(3) (+2)×(-3)
(+2):看作向右运动2米;
×(-3):看作沿反方向运动3次。
结果:向左运动6米。(+2)×(-3)= - 6
-6
-4
0
-2
2
右
2
(4) (-2)×(-3)
(-2):看作向左运动2米;
×(-3):看作沿反方向运动3次。
结果:向右运动6米。(-2)×(-3)=+6
2
6
0
2
6
4
-2
右
(5) 0 × 5 = 0
在原地0点运动5次
(-5)× 0 = 0
向原地-5点运动0次
结果:被乘数是0或者乘数是0,结果仍为0。
0 × 0 = 0
(1) 2×3=6
(2)(-2)×(-3)=6
(3)(-2)×3= -6
(4) 2×(-3)= -6
(5)被乘数或乘数为0时,结果是0
5个例子综合如下:
同号相乘 积为正数
异号相乘 积为负数
观察每个式子中的两个因数及积的符号,你能得到什么结论
正乘正得正,
正乘负得负,
负乘正得负,
负乘负得正。
异号得负
同号得正
两数的
符号特征 积的符号 积的绝对值
同 号
异 号
一个数
为0
有理数乘法法则:
+
-
绝对值相乘
绝对值相乘
得 0
先定符号,再定绝对值!
例1: (-7) ×(- 4)
(同号两数乘)
解:(-7)×(- 4)
=
(同号得正)
= + 28
(把绝对值相乘)
例2:(-5)×4×(-0.25)
(从左向右依次运算)
解:原式= 〔(-5)×4〕×(-0.25)
异号得负
绝对值相乘
同号得正
绝对值相乘
=+(20×0.25)
( 7×4 )
+
=〔-(5×4)〕×(-0.25)
=(-20)×(-0.25)
= 5
练习1:先确定下列积的号,然后试计算结果:
(1) 5×(-3)
(2) (-4)×6
(3)(-7)×(-9)
(4) 0.5×0.7
积的符号为负
积的符号为负
积的符号为正
积的符号为正
= -15
= -24
= 63
= 0.35
先确定积的符号,再把绝对值相乘。
练习2、计算(口答):
(1) 6×(-9)=
(2)(-6)×(-9)=
(3)(-6)×9 =
(4) (-6)×1=
(5) ( -6)×(-1) =
(6) 6×(-1) =
-54
54
-54
- 6
6
- 6
练习4、用“<”或“>”号填空:
(1)如果a<0 b>0那么 ab___0
(2)如果a<0 b<0那么 ab___0
练习3、计算:
(1) (-6) ×0.25 (2) (0.5)×(-8)
(- )×(- )
(4) (- )×0
25
6
=-1.5
=-4
=0
>
<
7
10
24
13
=
35
12
练习5、判断下列方程的解是正数、负数还是0:
(1) 4X= -16 (2)-3X=18
(3)-9X=-36 (4)-5X=0
练习6、思考题
(1)当a>0时,a与2a哪个大?
(2)当a<0时,a与2a那个大?
正数
负数
0
负数
2a大
a大
解: (1) (-3) ×(-9) = 27
(2) ( - ) × = -
(3) 7 × (-1) = -7
1
2
1
3
1
6
(-3)×(-9) (2) (- ) ×
7 ×(-1) (4) (-0.8) ×1
⑸(- ) ×(- ) ⑹(-3) ×(- )
1
2
1
3
3
8
8
3
1
3
(-0.8) ×1 = -0.8
⑸(- ) ×(- )=1
3
8
8
3
⑹(-3) ×(- )=1
1
3
观察(3)、(4)两题你有什么发现?能得出什么结论?
观察(5)、(6)两题你有什么发现?能得出什么结论?
练习7、看谁算的又快又对:
注意:
a、一个数同+1相乘,得原数;
一个数同-1相乘,得原数的相反数。
b、乘积为1的两个有理数互为倒数
C、零没有倒数(零作除数无意义)
跟 踪 练 习:
1、说出下列各数的倒数:
(1)-1 (2)-2
2、说出下列各式的结果:
(1) a×(—1)
(2) a× 1
跟 踪 练 习:
1、说出下列各数的倒数:
(1)-1 -1 (2)-2
2、说出下列各式的结果:
(1) a×(—1)
(2) a× 1
1
-
2
-
2
3
5
4
- a
a
3、计算下列各式:
3、计算下列各式:
(1) 5
(2) -1
观察下列各式,它们的积是正的还是负的?
(1) 4×5×0.25=
(2) (-4)×5×0.25=
(3) (-4)×(-5)×0.25=
(4) (-4)×(-5)×(-0.25)=
(5) (-4)×5×(-0.25)×0=
观察下列各式,它们的积是正的 还是负的?
(1) 4×5×0.25= 5
(2) (-4)×5×0.25= -5
(3) (-4)×(-5)×0.25= 5
(4) (-4)×(-5)×(-0.25)= -5
(5) (-4)×5×(-0.25)×0= 0
议一议:
几个有理数相乘,因数都不为0时,积的符号怎样确定?
有一个因数为0时,积是多少?
几个有理数相乘,积的符号由负因数的个数确定:
负因数的个数为偶数个,则积为正数
负因数的个数为奇数个,则积为负数
符号确定后再把绝对值相乘
当有一个因数为零时,积为零。
计算下列各式:
计算下列各式:
-42
7
3
-
5
6
0
1
6
-
4
35
本节课大家学会了什么?
有理数乘法法则如何叙述?
有理数乘法法则的探索采用了什么方法?
小结:
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。
2.如何进行两个有理数的运算:
先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。
注意:
a、一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。
b、乘积为1的两个有理数互为倒数,零没有倒数。
3、乘法法则的探索用到了猜想法和数轴验证法
达 标 检 测
1. 五个有理数的积是负数,则这五个数中负因数的个数是( )
1个 B. 3个 C. 5个 D. 一个或3个或5个
2、 3. 倒数是本身的数有 个,它们是 。
3、 计算(1)(-6) (-2 )=
(2)
(3)
4、下列说法正确的是( )
A、同号两数相乘,取原来的符号 B、两个数相乘,积大于任何一个乘数 C、一个数与0相乘仍得这个数 D、一个数与-1相乘,积为该数的相反数
达 标 检 测
1. 五个有理数的积是负数,则这五个数中负因数的个数是( D )
1个 B. 3个 C. 5个 D. 1个或3个或5个
2、 倒数是本身的数有 2 个,它们是 ±1 。
3、 计算(1)(-6) (-2 )= 14
(2) 5
(3) -1
4、下列说法正确的是(D )
A、同号两数相乘,取原来的符号 B、两个数相乘,积大于任何一个乘数 C、一个数与0相乘仍得这个数 D、一个数与-1相乘,积为该数的相反数
