24.5 三角形的内切圆 课件(共36张PPT)
文档属性
| 名称 | 24.5 三角形的内切圆 课件(共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 00:00:00 | ||
图片预览






文档简介
(共36张PPT)
第24章
圆
24.5
三角形的内切圆
沪科版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
4
CONTENTS
随堂演练
5
课后作业
6
知识小结
新课目标
1
学习目标
1.
了解有关三角形的内切圆和三角形的内心的概念.
2.
掌握三角形内心的性质并能加以应用.
(重点)
3.
学会利用方程思想解决几何问题,体验数形结合思
想.
(难点)
情景导学
2
小明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
情境引入
新课进行时
3
讲授新课
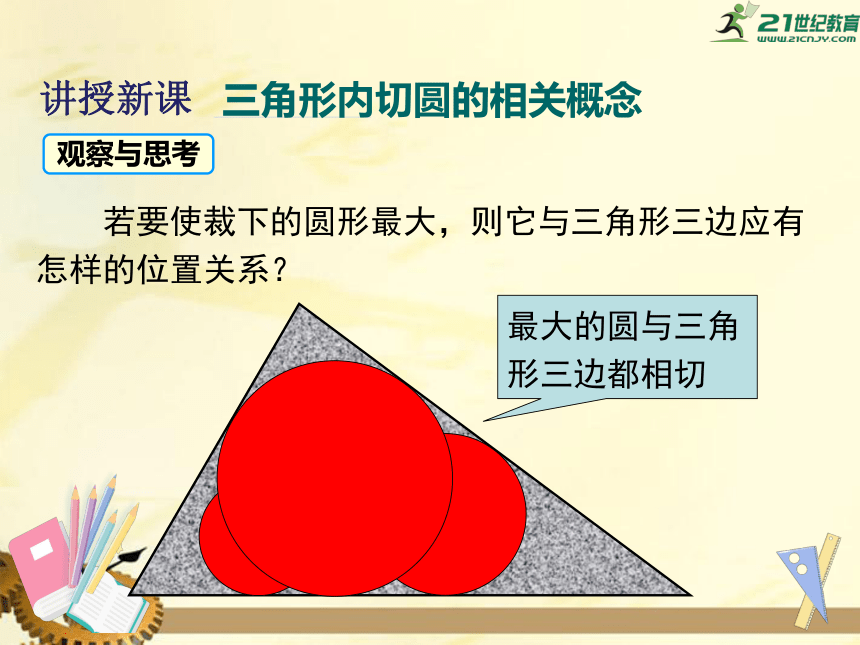
三角形内切圆的相关概念
若要使裁下的圆形最大,则它与三角形三边应有怎样的位置关系?
观察与思考
最大的圆与三角形三边都相切
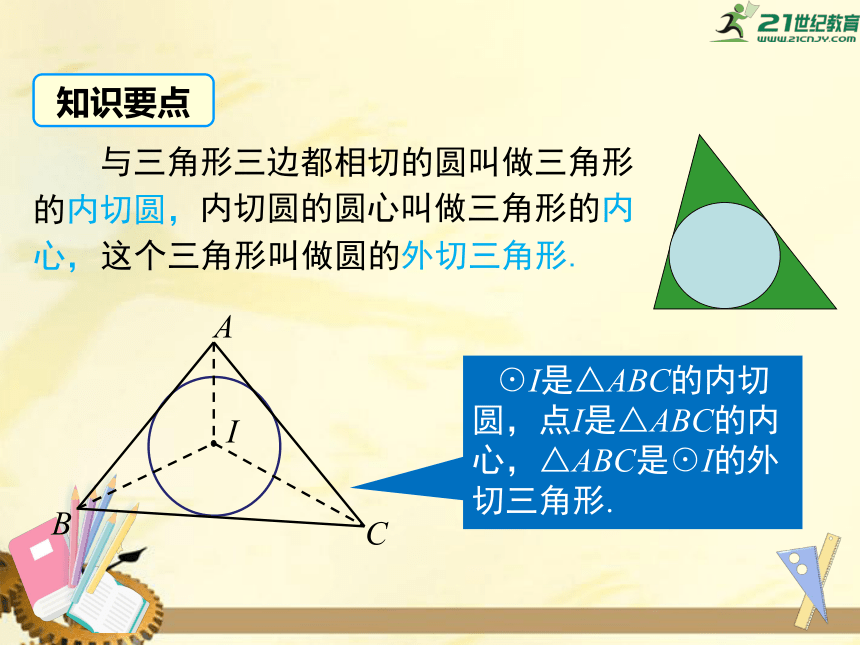
与三角形三边都相切的圆叫做三角形的内切圆,
内切圆的圆心叫做三角形的内
心,
这个三角形叫做圆的外切三角形.
B
A
C
I
☉I是△ABC的内切圆,点I是△ABC的内心,△ABC是☉I的外切三角形.
知识要点
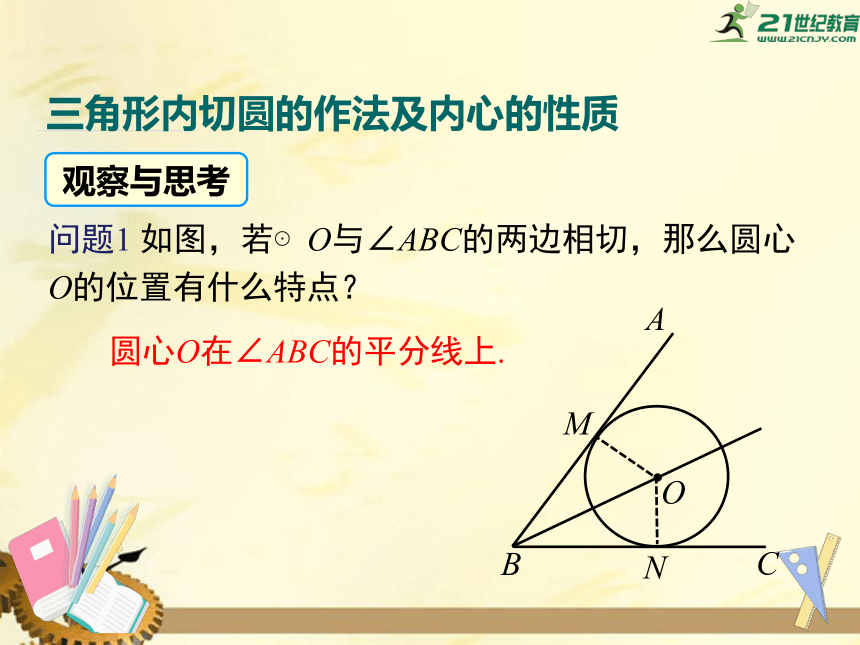
三角形内切圆的作法及内心的性质
观察与思考
问题1
如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?
圆心O在∠ABC的平分线上.
N
C
O
M
A
B
C
O
A
B
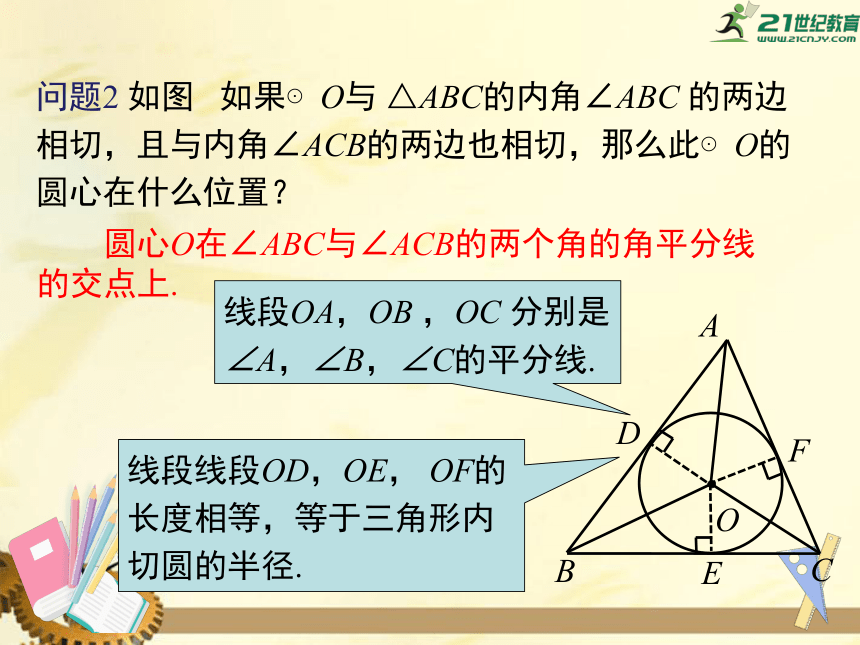
问题2
如图
如果⊙O与
△ABC的内角∠ABC
的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?
圆心O在∠ABC与∠ACB的两个角的角平分线的交点上.
线段OA,OB
,OC
分别是∠A,∠B,∠C的平分线.
F
E
D
线段线段OD,OE,
OF的长度相等,等于三角形内切圆的半径.
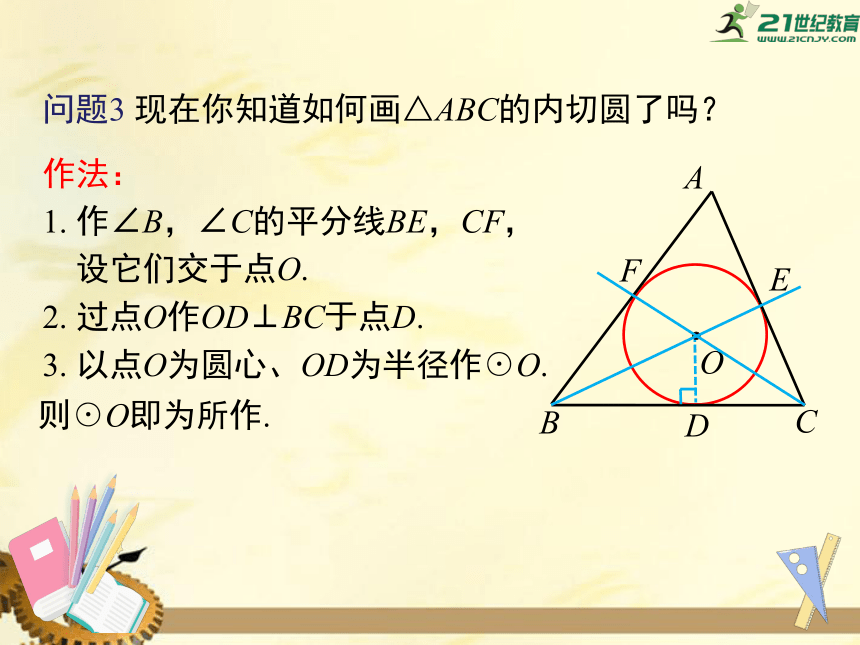
作法:
1.
作∠B,∠C的平分线BE,CF,
设它们交于点O.
2.
过点O作OD⊥BC于点D.
3.
以点O为圆心、OD为半径作☉O.
则☉O即为所作.
问题3
现在你知道如何画△ABC的内切圆了吗?
C
O
A
B
F
E
D
三角形内心的性质:
三角形的内心在三角形的角平分线上.
三角形的内心到三角形的三边距离相等.
知识要点
C
O
A
B
F
E
D
例1
如图,△ABC中,∠
B=43°,∠C=61
°,点
I
是△ABC的内心,求∠
BIC的度数.
解:连接IB,IC.
A
B
C
I
∵点
I
是△ABC的内心,
∴
IB,IC
分别是∠
B,∠C的平分线.
在△IBC中,
典例精析
例2
如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱.
圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为3cm,求圆柱底面圆的半径.
该木模可以抽象为几何如下几何图形.
C
A
B
r
O
D
解:
如图,设圆O切AB于点D,连接OA、OB、OD.
∵圆O是△ABC的内切圆,
∴AO、BO是∠BAC、∠ABC的角平分线
∵
△ABC是等边三角形,
∴
∠OAB=∠OBA=30o
∵OD⊥AB,AB=3cm,
∴AD=BD=
AB=1.5(cm)
∴OD=AD·
tan30o=
(cm)
答:圆柱底面圆的半径为
cm.
例3
△ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
想一想:图中你能找出哪些相等的线段?理由是什么?
B
A
C
E
D
F
O
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=9-x(cm),
BF=BD=AB-AF=13-x(cm).
由
BD+CD=BC,可得
(13-x)+(9-x)=14,
∴
AF=4(cm),BD=9(cm),CE=5(cm).
方法小结:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
解得
x=4.
A
C
E
D
F
O
比一比
名称
确定方法
图形
性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边
中垂线的交
点
1.OA=OB=OC
2.外心不一定在三角形的内部.
三角形三条
角平分线的
交点
1.到三边的距离相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
A
B
O
A
B
C
O
C
A
B
O
D
1.求边长为6
cm的等边三角形的内切圆半径与外接圆半径.
解:如图,由题意可知BC=6cm,
∠ABC=60°,OD⊥BC,OB平分∠ABC.
∴∠OBD=30°,BD=3cm,△OBD为直角三角形.
内切圆半径
外接圆半径
练一练
变式:
求边长为a的等边三角形的内切圆半径r与外接圆半径R的比.
sin∠OBD=sin30=
C
A
B
R
r
O
D
A
B
C
O
D
E
F
A
B
C
D
E
F
O
2.设△ABC的面积为S,周长为L,
△ABC内切圆
的半径为r,则S,L与r之间存在怎样的数量关系?
A
B
C
O
c
D
E
r
3.如图,直角三角形的两直角边分别是a、b,斜边为c,则其内切圆的半径r为___________(以含a、b、c的代数式表示r).
解析:过点O分别作AC,BC,AB的垂线,垂足分别为D,E,F.
F
则AD=AC-DC=b-r,
BF=BC-CE=a-r,
因为AF=AD,BF=BE,AF+BF=c,
所以a-r+b-r=c,
所以
随堂演练
4
(3)若∠BIC=100
°,则∠A
=
度.
当堂练习
(2)若∠A=80
°,则∠BIC
=
度.
130
20
1.如图,在△ABC中,点I是内心,
(1)若∠ABC=50°,
∠ACB=70°,∠BIC=_____.
A
B
C
I
(4)试探索:
∠A与∠BIC之间存在怎样的数量关系?
120°
2.《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步.”该问题的答案是____步.
6
解析:先由勾股定理得出斜边的长,再根据公式
求出该直角三角形内切圆的半径,即可得起至今的长度.
3.如图,⊙O与△ABC的三条边所得的弦长相等,则下列说法正确的是( )
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形
解析:过O作OM⊥AB于M,ON⊥BC于N,OQ⊥AC于Q,连接OK、OD、OF,根据垂径定理和已知求出DM=KQ=FN,根据勾股定理求出OM=ON=OQ,即点O是△ABC的内心.故选A
A
4.如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:DI=DB.
证明:连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴BD=ID.
拓展提升
直角三角形的两直角边分别是3cm
,4cm,试问:
(1)它的外接圆半径是
cm;内切圆半径是
cm?
(2)若移动点O的位置,使☉O保持与△ABC的边AC、BC都相切,求☉O的半径r的取值范围.
·
A
B
C
E
D
F
O
5
1
解:如图所示,设与BC、AC相切的最大圆与BC、AC的切点分别为B、D,连接OB、OD,则四边形BODC为正方形.
·
A
B
O
D
C
∴OB=BC=3,
∴半径r的取值范围为0<r≤3.
知识小结
5
课堂小结
三角形内切圆
运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
有关概念
内心概念及性质
应用
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第24章
圆
24.5
三角形的内切圆
沪科版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
4
CONTENTS
随堂演练
5
课后作业
6
知识小结
新课目标
1
学习目标
1.
了解有关三角形的内切圆和三角形的内心的概念.
2.
掌握三角形内心的性质并能加以应用.
(重点)
3.
学会利用方程思想解决几何问题,体验数形结合思
想.
(难点)
情景导学
2
小明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
情境引入
新课进行时
3
讲授新课
三角形内切圆的相关概念
若要使裁下的圆形最大,则它与三角形三边应有怎样的位置关系?
观察与思考
最大的圆与三角形三边都相切
与三角形三边都相切的圆叫做三角形的内切圆,
内切圆的圆心叫做三角形的内
心,
这个三角形叫做圆的外切三角形.
B
A
C
I
☉I是△ABC的内切圆,点I是△ABC的内心,△ABC是☉I的外切三角形.
知识要点
三角形内切圆的作法及内心的性质
观察与思考
问题1
如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?
圆心O在∠ABC的平分线上.
N
C
O
M
A
B
C
O
A
B
问题2
如图
如果⊙O与
△ABC的内角∠ABC
的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?
圆心O在∠ABC与∠ACB的两个角的角平分线的交点上.
线段OA,OB
,OC
分别是∠A,∠B,∠C的平分线.
F
E
D
线段线段OD,OE,
OF的长度相等,等于三角形内切圆的半径.
作法:
1.
作∠B,∠C的平分线BE,CF,
设它们交于点O.
2.
过点O作OD⊥BC于点D.
3.
以点O为圆心、OD为半径作☉O.
则☉O即为所作.
问题3
现在你知道如何画△ABC的内切圆了吗?
C
O
A
B
F
E
D
三角形内心的性质:
三角形的内心在三角形的角平分线上.
三角形的内心到三角形的三边距离相等.
知识要点
C
O
A
B
F
E
D
例1
如图,△ABC中,∠
B=43°,∠C=61
°,点
I
是△ABC的内心,求∠
BIC的度数.
解:连接IB,IC.
A
B
C
I
∵点
I
是△ABC的内心,
∴
IB,IC
分别是∠
B,∠C的平分线.
在△IBC中,
典例精析
例2
如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱.
圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为3cm,求圆柱底面圆的半径.
该木模可以抽象为几何如下几何图形.
C
A
B
r
O
D
解:
如图,设圆O切AB于点D,连接OA、OB、OD.
∵圆O是△ABC的内切圆,
∴AO、BO是∠BAC、∠ABC的角平分线
∵
△ABC是等边三角形,
∴
∠OAB=∠OBA=30o
∵OD⊥AB,AB=3cm,
∴AD=BD=
AB=1.5(cm)
∴OD=AD·
tan30o=
(cm)
答:圆柱底面圆的半径为
cm.
例3
△ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
想一想:图中你能找出哪些相等的线段?理由是什么?
B
A
C
E
D
F
O
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=9-x(cm),
BF=BD=AB-AF=13-x(cm).
由
BD+CD=BC,可得
(13-x)+(9-x)=14,
∴
AF=4(cm),BD=9(cm),CE=5(cm).
方法小结:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
解得
x=4.
A
C
E
D
F
O
比一比
名称
确定方法
图形
性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边
中垂线的交
点
1.OA=OB=OC
2.外心不一定在三角形的内部.
三角形三条
角平分线的
交点
1.到三边的距离相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
A
B
O
A
B
C
O
C
A
B
O
D
1.求边长为6
cm的等边三角形的内切圆半径与外接圆半径.
解:如图,由题意可知BC=6cm,
∠ABC=60°,OD⊥BC,OB平分∠ABC.
∴∠OBD=30°,BD=3cm,△OBD为直角三角形.
内切圆半径
外接圆半径
练一练
变式:
求边长为a的等边三角形的内切圆半径r与外接圆半径R的比.
sin∠OBD=sin30=
C
A
B
R
r
O
D
A
B
C
O
D
E
F
A
B
C
D
E
F
O
2.设△ABC的面积为S,周长为L,
△ABC内切圆
的半径为r,则S,L与r之间存在怎样的数量关系?
A
B
C
O
c
D
E
r
3.如图,直角三角形的两直角边分别是a、b,斜边为c,则其内切圆的半径r为___________(以含a、b、c的代数式表示r).
解析:过点O分别作AC,BC,AB的垂线,垂足分别为D,E,F.
F
则AD=AC-DC=b-r,
BF=BC-CE=a-r,
因为AF=AD,BF=BE,AF+BF=c,
所以a-r+b-r=c,
所以
随堂演练
4
(3)若∠BIC=100
°,则∠A
=
度.
当堂练习
(2)若∠A=80
°,则∠BIC
=
度.
130
20
1.如图,在△ABC中,点I是内心,
(1)若∠ABC=50°,
∠ACB=70°,∠BIC=_____.
A
B
C
I
(4)试探索:
∠A与∠BIC之间存在怎样的数量关系?
120°
2.《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步.”该问题的答案是____步.
6
解析:先由勾股定理得出斜边的长,再根据公式
求出该直角三角形内切圆的半径,即可得起至今的长度.
3.如图,⊙O与△ABC的三条边所得的弦长相等,则下列说法正确的是( )
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形
解析:过O作OM⊥AB于M,ON⊥BC于N,OQ⊥AC于Q,连接OK、OD、OF,根据垂径定理和已知求出DM=KQ=FN,根据勾股定理求出OM=ON=OQ,即点O是△ABC的内心.故选A
A
4.如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:DI=DB.
证明:连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴BD=ID.
拓展提升
直角三角形的两直角边分别是3cm
,4cm,试问:
(1)它的外接圆半径是
cm;内切圆半径是
cm?
(2)若移动点O的位置,使☉O保持与△ABC的边AC、BC都相切,求☉O的半径r的取值范围.
·
A
B
C
E
D
F
O
5
1
解:如图所示,设与BC、AC相切的最大圆与BC、AC的切点分别为B、D,连接OB、OD,则四边形BODC为正方形.
·
A
B
O
D
C
∴OB=BC=3,
∴半径r的取值范围为0<r≤3.
知识小结
5
课堂小结
三角形内切圆
运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
有关概念
内心概念及性质
应用
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
