勾股定理的应用

(共14张PPT)
苏教版八年级数学上册
B
C
如图,太阳能热水器的支架AB长为90cm,与AB垂直的BC长为120cm.太阳能真空管AC有多长
A
B
C
90cm
120cm

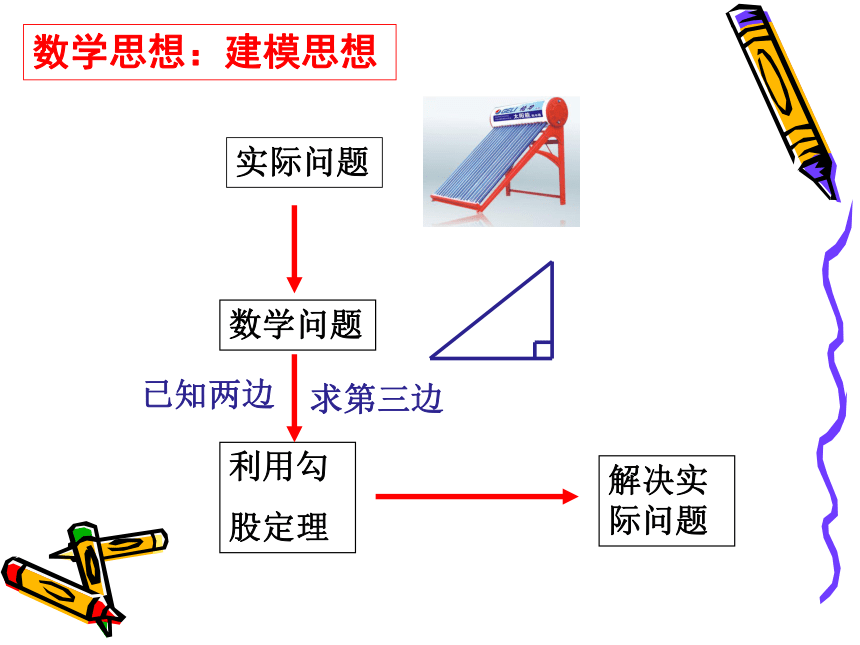
实际问题
数学问题
利用勾
股定理
已知两边
求第三边
数学思想：建模思想
解决实际问题
B
A
C
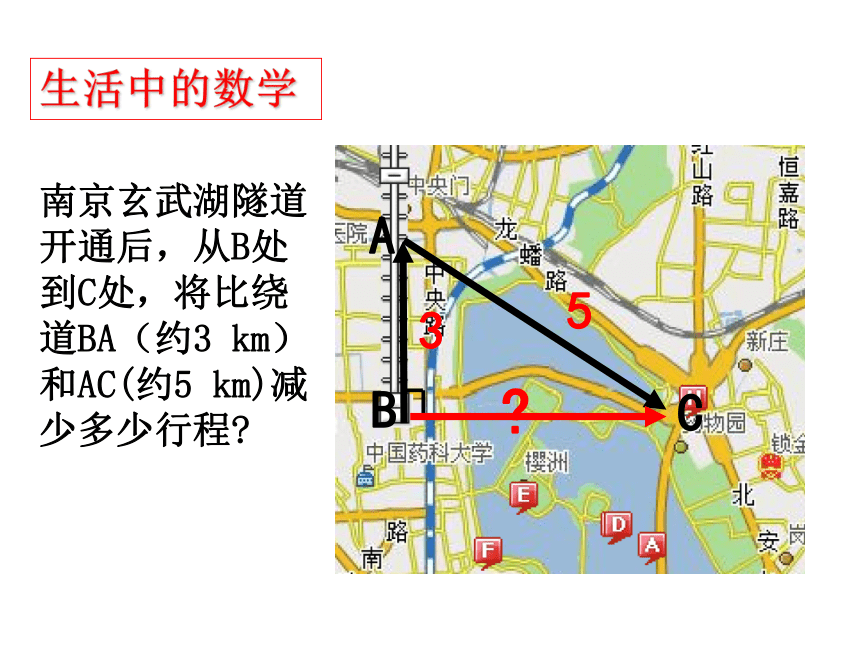
南京玄武湖隧道开通后，从B处到C处，将比绕道BA（约3 km）和AC(约5 km)减少多少行程
3
5

生活中的数学
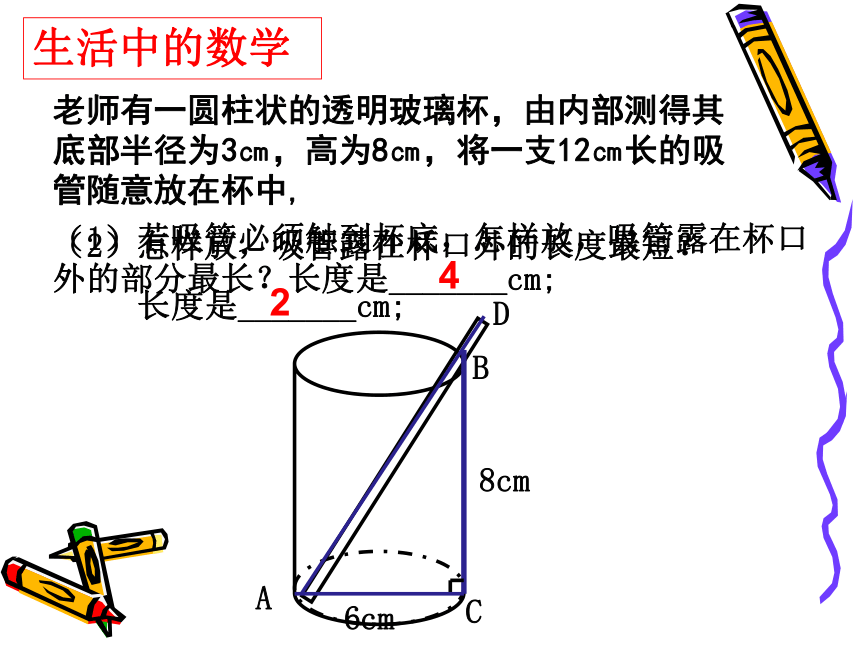
老师有一圆柱状的透明玻璃杯，由内部测得其底部半径为3㎝，高为8㎝，将一支12㎝长的吸管随意放在杯中,
A
C
B
D
6cm
8cm
（1）若吸管必须触到杯底，怎样放，吸管露在杯口外的部分最长？长度是_______cm;
4
（2）怎样放，吸管露在杯口外的长度最短？
长度是_______cm;
2
生活中的数学
生活中的疑问
周一升旗仪式的时候，八（2）班的小王同学看着冉冉升起的五星红旗突发奇想，学校的旗杆到底有多高呢？能用所学的数学知识来计算吗？
图（1）
图（2）
A
B
C
小王通过测量发现：
旗杆上的绳子垂到地面还多1米，如图（1），当他把绳子的下端拉开5米后，发现下端刚好接触地面，如图（2），
你能帮小王把旗杆的高度计算出来吗？
数学思想：方程思想
A
B
C
x
x+1
5
在Rt△ABC中，由勾股定理可得
X +5 =（x+1）
解得x=12
即旗杆的高度为12米。
方法指导：
在直角三角形中，如果已知一边以及另两边之间的数量关系，可以通过设未知数，利用勾股定理建立方程，从而求出三边的长度。
独立完成小练静的湖面上，有一支红莲，高出水面1米，一阵风吹来，红莲吹到一边，花朵齐及水面，已知红莲移动的水平距离为2m，求这里的水深是多少米？
老师提醒：
画图很重要，要找到图中图中已知的
直角三角形。
如图，有两棵树，一棵高8m，另一棵高2m，两树相距8m，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了（ ）
A.7m B.8m C.9m D.10m
8m
2m
8m
A
B
C
两点之间，线段最短
方法指导：构造直角三角形是运用勾股定理的重要途径。
D
数学思想：转化思想
如图,一架长为10m的梯子AB斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么它的底端是否也滑动1 m
A
B
C
10
8
A’
B’
生活中的数学
如果梯子的顶端下滑2米，
那么它的底端是否也滑动2米呢？
小结：
1、回忆本节课所学内容，你学会了用勾股定理解决哪些实际问题？
2、你在运用勾股定理解决实际问题时有哪些心得？哪些方法？
完成课堂检测！