苏科版八年级数学上册 6.3一次函数应用(图像综合)填空题拔高训练(二)(Word版 含解析)
文档属性
| 名称 | 苏科版八年级数学上册 6.3一次函数应用(图像综合)填空题拔高训练(二)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 115.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 17:52:05 | ||
图片预览


文档简介
八年级
第六章
一次函数应用(图像综合)
填空题拔高训练(二)
1.武汉疫情爆发期间,大学生小玲和小丽应聘成为了阳光小区的疫情防控志愿者.一天早晨,小玲从阳光小区出发骑三轮车匀速到距离7500米处的区疾病防控中心领取防疫物资,出发一段时间后,小丽发现小玲忘记带了社区介绍信,立即骑自行车沿小玲行驶的路线匀速行驶去追赶,当小丽追上小玲后,立即将介绍信交给了她,并用2分钟时间与小玲核对了一下防疫物资的清单,然后小玲继续以原速度前往区疾病防控中心,而小丽则按原路以原来速度的一半匀速返回阳光小区.设小丽与小玲之间的距离y(米)与小玲从阳光小区出发后的时间x(分)之间的关系如图所示.当小丽刚好返回到阳光小区时,小玲离区疾病防控中心的距离还有
米.
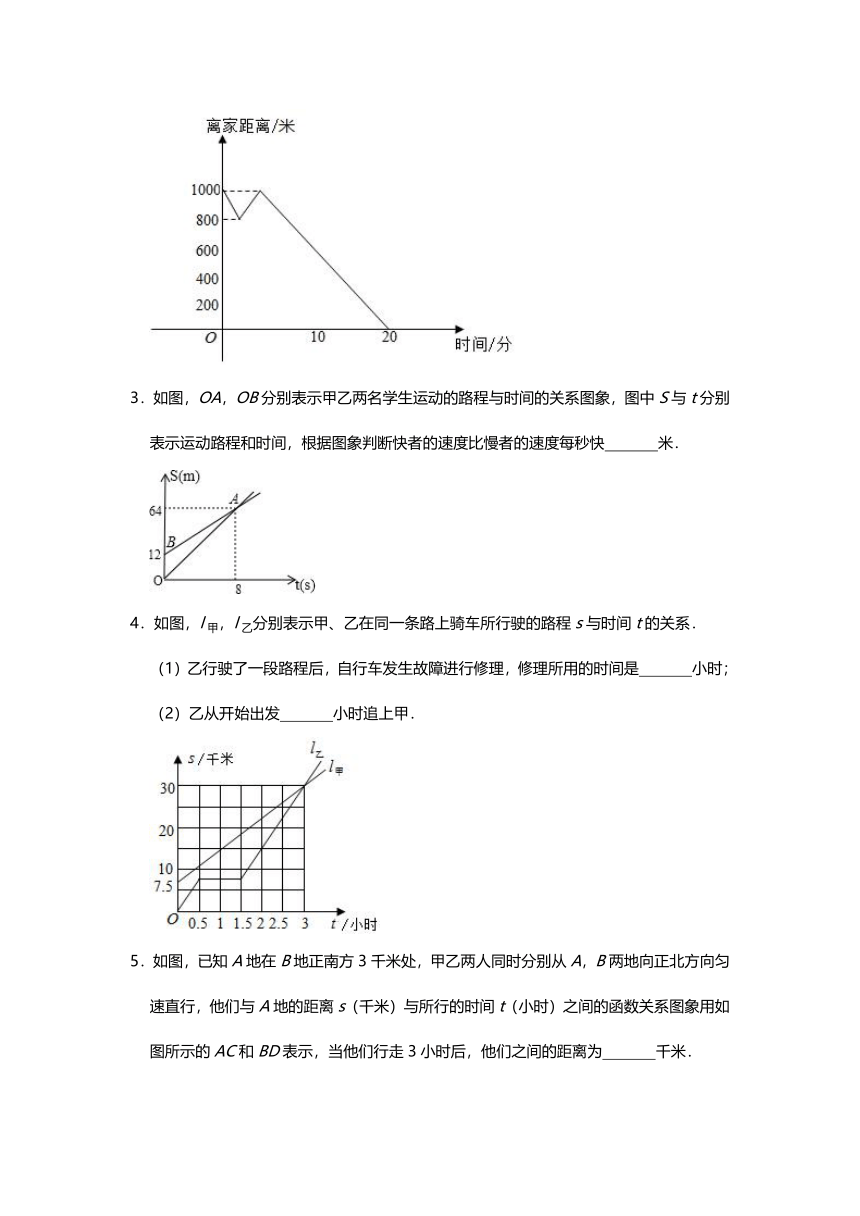
2.小敏从学校步行回家,突然想起忘记带家庭作业,他又返回了学校,拿了家庭作业,然后步行回家.图表显示了不同时间他离家的距离.问他一共走了
米路才到家.
3.如图,OA,OB分别表示甲乙两名学生运动的路程与时间的关系图象,图中S与t分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快
米.
4.如图,l甲,l乙分别表示甲、乙在同一条路上骑车所行驶的路程s与时间t的关系.
(1)乙行驶了一段路程后,自行车发生故障进行修理,修理所用的时间是
小时;
(2)乙从开始出发
小时追上甲.
5.如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A,B两地向正北方向匀速直行,他们与A地的距离s(千米)与所行的时间t(小时)之间的函数关系图象用如图所示的AC和BD表示,当他们行走3小时后,他们之间的距离为
千米.
6.甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.4.其中说法正确的是
(填写序号).
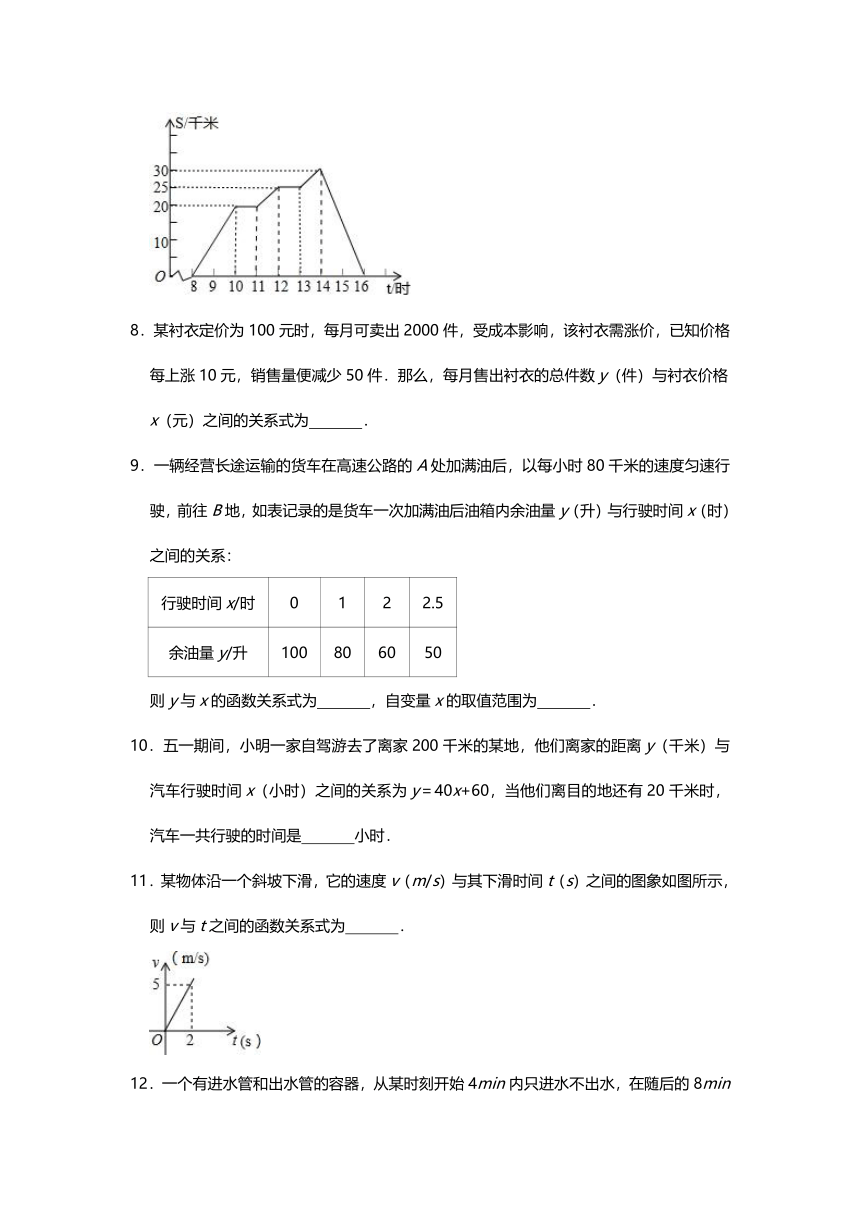
7.周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离家的距离S(千米)与时间t(时)之间的函数关系可以用图中的折线表示.现有如下信息:
(1)小李到达离家最远的地方的时间是14时;
(2)小李第一次休息时间是10时;
(3)11时到12时,小李骑了5千米;
(4)返回时,小李的平均车速是10千米/时.
其中,正确的信息有
(填序号).
8.某衬衣定价为100元时,每月可卖出2000件,受成本影响,该衬衣需涨价,已知价格每上涨10元,销售量便减少50件.那么,每月售出衬衣的总件数y(件)与衬衣价格x(元)之间的关系式为
.
9.一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶,前往B地,如表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x/时
0
1
2
2.5
余油量y/升
100
80
60
50
则y与x的函数关系式为
,自变量x的取值范围为
.
10.五一期间,小明一家自驾游去了离家200千米的某地,他们离家的距离y(千米)与汽车行驶时间x(小时)之间的关系为y=40x+60,当他们离目的地还有20千米时,汽车一共行驶的时间是
小时.
11.某物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)之间的图象如图所示,则v与t之间的函数关系式为
.
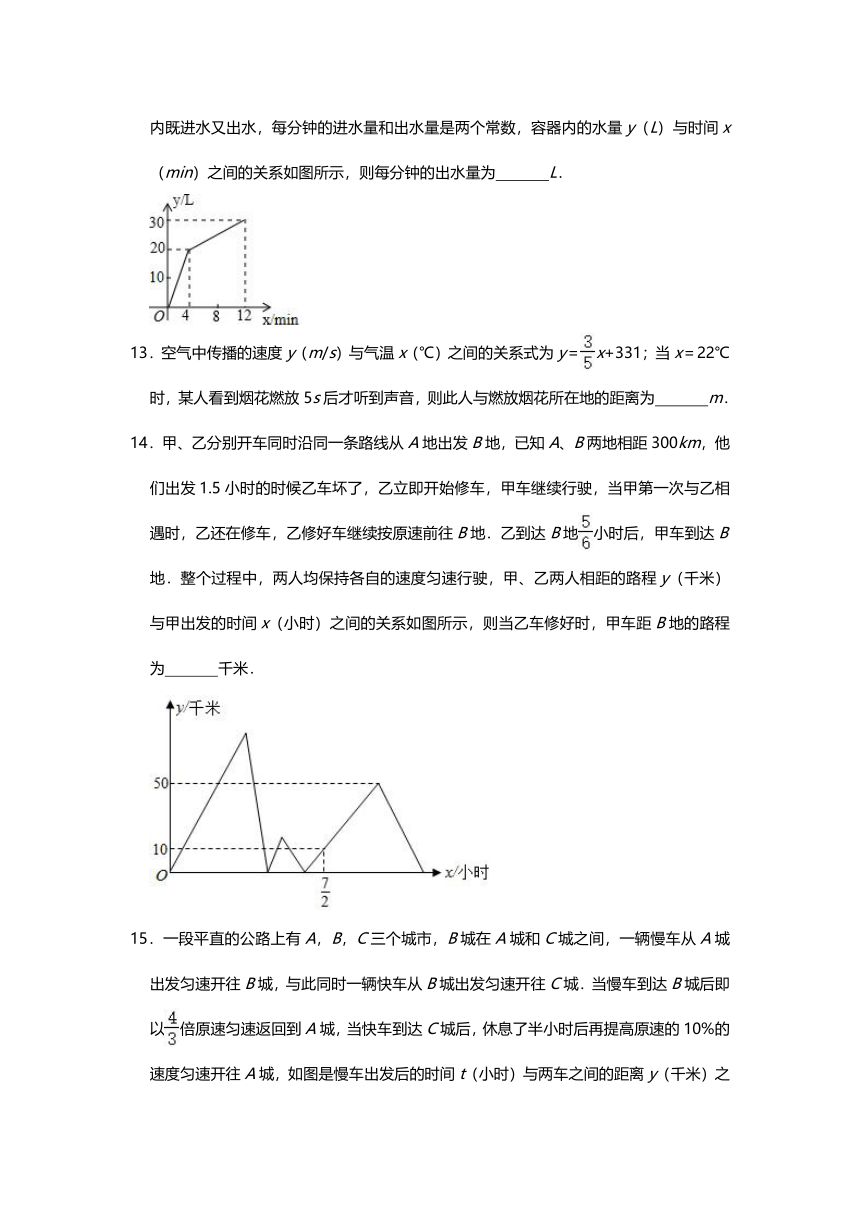
12.一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为
L.
13.空气中传播的速度y(m/s)与气温x(℃)之间的关系式为y=x+331;当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为
m.
14.甲、乙分别开车同时沿同一条路线从A地出发B地,已知A、B两地相距300km,他们出发1.5小时的时候乙车坏了,乙立即开始修车,甲车继续行驶,当甲第一次与乙相遇时,乙还在修车,乙修好车继续按原速前往B地.乙到达B地小时后,甲车到达B地.整个过程中,两人均保持各自的速度匀速行驶,甲、乙两人相距的路程y(千米)与甲出发的时间x(小时)之间的关系如图所示,则当乙车修好时,甲车距B地的路程为
千米.
15.一段平直的公路上有A,B,C三个城市,B城在A城和C城之间,一辆慢车从A城出发匀速开往B城,与此同时一辆快车从B城出发匀速开往C城.当慢车到达B城后即以倍原速匀速返回到A城,当快车到达C城后,休息了半小时后再提高原速的10%的速度匀速开往A城,如图是慢车出发后的时间t(小时)与两车之间的距离y(千米)之间的函数关系图,慢车出发6小时后,两车相距
千米.
16.10月期间,我市庆祝新中国成立70周年“祖国万岁”的主题灯光秀展示了两江四岸流光溢彩的壮美之景.周末,小明和小华相约一起乘轻轨去看灯光秀.已知小明家、轻轨站和小华家顺次分布在同一条笔直的公路上.小明、小华打算以各自的速度步行到轻轨站,小明出发3分钟后,小华从家里出发,走了两分钟,小华想起没带相机,立即掉头以原速的返回家中取相机,并在家中取停留5分钟,发现时间来不及便立即打车前住轻轨站,最终比小明早到2分钟.如图是两人之间的距离与小华出发时间之间的关系,则小明家离轻轨站的距离比小华家离轻轨站的距离少
米.
17.重庆某著名景区依托天然河道新开发了一款乘船体验项目.小明乘船由甲地顺流而下到乙地,然后由乙地逆流而上到丙地,然后靠岸乘车离开景点.若水流速度为2km/小时,船在静水中的速度为8km/小时.在整个乘船过程中,轮船与甲地相距的路程S(千米)与轮船出发的时间t(小时)之间的关系如图所示,甲乙两地间的距离为
千米.
18.一辆汽车开始行驶时,油箱内有油45升,如果每小时耗油6.5升,则这辆汽车油箱内剩余油量Q(升)与行驶时间t(小时)之间的关系式为
,且当t=4时,Q=
升.
19.为庆中国华诞70周年,国庆期间电影院推出了一系列爱国大片,其中《我和我的祖国》票房最高,学校为了对学生进行爱国主义教育,给每位学生发了张此片的电影票.明明在电影院门口发现忘记带电影票,遂边打电话给父亲边往家走,希望父亲能帮忙送来.1分钟后,父亲在家找到票开始往电影院走,再过8分钟两人相遇,父亲立即将票给明明,明明马上把速度提高到原来的倍跑向电影院,30秒后两人相距60米时,父亲才以不变的速度返家.两人的距离y(米)与明明出发的时间x(分)之间的关系如图所示,则当明明回到电影院门口时,父亲离家还有
米.
20.一条笔直的公路上顺次有A、B、C三地,小明驾车从B地出发匀速行驶前往A地,到达A地后停止,在小明出发的同时,小李驾车从B地出发匀速行驶前往A地,到达A地停留2小时后,调头按原速向C地行驶,若AB两地相距200千米,在行驶的过程中,两人之间的距离y(千米)与小李驾驶时间x(小时)之间的函数图象如图所示,则在他们出发后经过
小时相遇.
参考答案
1.解:由图象得:小玲骑车速度:7500÷30=250(米/分),
由函数图象得出,小丽在小玲5分后出发,12.5分时追上小玲,
设小丽去时的速度为v米/分,
(12.5﹣5)v=12.5×250,
v=,
则小丽回家的时间:=15(分钟),
当小丽刚好返回到阳光小区时,小玲离区疾病防控中心的距离为:250×(32﹣15﹣14.5)=625(米).
故答案为:625.
2.解:小敏一共走了:(1000﹣800)×2+1000=1400(米).
故答案为:1400.
3.解:观察图象知:甲跑64米用时8秒,速度为8m/s,
乙行驶52米用时8秒,速度为6.5m/s,
速度差为8﹣6.5=1.5m/s,
故答案为1.5.
4.解:(1)1.5﹣0.5=1(小时),
即修理所用的时间是1小时;
(2)由题意可知,乙从开始出发3小时追上甲.
故答案为:(1)1;(2)3.
5.解:由题,图可知甲走的是C路线,乙走的是D路线,
设s=kt+b①,
因为C过(0,0),(2,4)点,
所以代入①得:k=2,b=0,
所以sC=2t.
因为D过(2,4),(0,3)点,
代入①中得:k=,b=3,
所以sD=t+3,
当t=3时,sC﹣sD=6﹣=.
故答案为:
6.解:由图象可知,乙出发时,甲乙相距80km,2小时后,乙车追上甲.则说明乙每小时比甲快40km,则乙的速度为120km/h.①正确;
由图象第2﹣6小时,乙由相遇点到达B,用时4小时,每小时比甲快40km,则此时甲乙距离4×40=160km,则m=160,②正确;
当乙在B休息1h时,甲前进80km,则H点坐标为(7,80),③正确;
乙返回时,甲乙相距80km,到两车相遇用时80÷(120+80)=0.4小时,则n=6+1+0.4=7.4,④正确,
故答案为:①②③④.
7.解:由图象可得,
小李到达离家最远的地方的时间是14时,故(1)正确;
小李第一次休息时间是10时,故(2)正确;
11时到12时,小李骑了25﹣20=5(千米),故(3)正确;
返回时,小李的平均车速是30÷(16﹣14)=15(千米/小时),故(4)错误;
故答案为:(1)(2)(3).
8.解:由题意可得,
y=2000﹣×50=﹣5x+2500,
故答案为:y=﹣5x+2500.
9.解:设y与x之间的关系为一次函数,其函数表达式为y=kx+b,
将(0,100),(1,80)代入上式得,
,解得,
∴y=﹣20x+100;
100÷20=5,
∴0≤x≤5.
故答案为:y=﹣20x+100;0≤x≤5.
10.解:由题意可得,
当他们离目的地还有20千米时,则y=180,
当y=180时,180=40x+60,
解得,x=3,
即当他们离目的地还有20千米时,汽车一共行驶的时间是3小时,
故答案为:3.
11.解:设函数解析式为v=kt,
将点(2,5)代入得:5=2k,解得:k=,
∴v与t之间的函数解析式为v=(t≥0).
故答案为:v=(t≥0).
12.解:由图象可得,
每分钟的进水量为:20÷4=5(L),
每分钟的出水量为:5﹣(30﹣20)÷(12﹣4)=5﹣10÷8=5﹣1.25=3.75(L),
故答案为:3.75.
13.解:当x=22时,y=×22+331=344.2,
则当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为:344.2×5=1721(m),
故答案为:1721.
14.解:∵甲车速度==60千米/时,
∴甲车走完全程时间==5小时,
∴乙车速度=60+=120千米/时,
设乙车修了x小时,
由题意可得:120(﹣x)﹣60×=10,
∴x=,
∴当乙车修好时,甲车距B地的路程=300﹣60×(+)=110千米,
故答案为:110.
15.解:由题意可知A,B两地的距离为240千米;慢车用了4小时到达B地;
故慢车原速为:240÷4=60千米/时;
∴快车原速为:60+(320﹣240)÷2=100千米/时;
B,C两地的距离为:100×2=200千米,
∴慢车出发6小时后,两车相距为:(6﹣2﹣0.5)×100×(1+10%)﹣200﹣(6﹣4)×60×=25千米.
故答案为:25
16.解:由图象可得:小华到轻轨站时,小明家轻轨站的距离为240米,
∴小明的速度==120米/分,
∴小明家离轻轨站的距离=120×(12.5+3)=1860米,
设小华速度为x米/分,
∵小华家离轻轨站的距离=3120﹣[1860﹣120×(2+3+5+)]=2640米,
∵2640﹣1860=780米
∴小明家离轻轨站的距离比小华家离轻轨站的距离少780米,
故答案为:780.
17.解:根据图形可知甲、丙两地间的距离为2km.
(1)丙在甲地和乙地之间,设甲乙两地距离为x,
则,
解得:x=12.5.
(2)丙不在甲地和乙地之间,设甲乙两地距离为x,
则,
解得:x=10.
∴甲乙两地间的距离为12.5km或10km.
故答案为:12.5或10
18.解:依题意,得:Q=﹣6.5t+45.
当t=4时,Q=﹣6.5t+45=19.
故答案为:Q=﹣6.5t+45;19.
19.解:由题意可得,
返回时明明的速度为:(米/分),
∴返回前明明的速度为:120×=90(米/分),
设爸爸的速度为x米/分钟,根据题意得,
8(90+x)=1450﹣90×1,
解得x=80,
∴爸爸的速度为80米/分钟,
明明从电影院到相遇所走路程为:90×9=810(米),
爸爸从家到相遇所走路程为:80×8=640(米),
明明返回时所用时间为:,
此时爸爸走了:80×()=500(米),
∴当明明回到电影院门口时,父亲与家的距离为:640﹣500=140(米).
故答案为:140
20.解:∵最终两车相距400千米,
∴A、C两地相距400千米.
小李的速度为(200+400)÷(8﹣2)=100(千米/小时),
小李从B到达A地的时间为200÷100=2(小时),
小明的速度为(200﹣120)÷3=40(千米/小时),
小李从A地返回时,两车的间距为200﹣40×4=40(千米),
两车相遇的时间为4+=4(小时)
故答案为:4.
第六章
一次函数应用(图像综合)
填空题拔高训练(二)
1.武汉疫情爆发期间,大学生小玲和小丽应聘成为了阳光小区的疫情防控志愿者.一天早晨,小玲从阳光小区出发骑三轮车匀速到距离7500米处的区疾病防控中心领取防疫物资,出发一段时间后,小丽发现小玲忘记带了社区介绍信,立即骑自行车沿小玲行驶的路线匀速行驶去追赶,当小丽追上小玲后,立即将介绍信交给了她,并用2分钟时间与小玲核对了一下防疫物资的清单,然后小玲继续以原速度前往区疾病防控中心,而小丽则按原路以原来速度的一半匀速返回阳光小区.设小丽与小玲之间的距离y(米)与小玲从阳光小区出发后的时间x(分)之间的关系如图所示.当小丽刚好返回到阳光小区时,小玲离区疾病防控中心的距离还有
米.
2.小敏从学校步行回家,突然想起忘记带家庭作业,他又返回了学校,拿了家庭作业,然后步行回家.图表显示了不同时间他离家的距离.问他一共走了
米路才到家.
3.如图,OA,OB分别表示甲乙两名学生运动的路程与时间的关系图象,图中S与t分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快
米.
4.如图,l甲,l乙分别表示甲、乙在同一条路上骑车所行驶的路程s与时间t的关系.
(1)乙行驶了一段路程后,自行车发生故障进行修理,修理所用的时间是
小时;
(2)乙从开始出发
小时追上甲.
5.如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A,B两地向正北方向匀速直行,他们与A地的距离s(千米)与所行的时间t(小时)之间的函数关系图象用如图所示的AC和BD表示,当他们行走3小时后,他们之间的距离为
千米.
6.甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.4.其中说法正确的是
(填写序号).
7.周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离家的距离S(千米)与时间t(时)之间的函数关系可以用图中的折线表示.现有如下信息:
(1)小李到达离家最远的地方的时间是14时;
(2)小李第一次休息时间是10时;
(3)11时到12时,小李骑了5千米;
(4)返回时,小李的平均车速是10千米/时.
其中,正确的信息有
(填序号).
8.某衬衣定价为100元时,每月可卖出2000件,受成本影响,该衬衣需涨价,已知价格每上涨10元,销售量便减少50件.那么,每月售出衬衣的总件数y(件)与衬衣价格x(元)之间的关系式为
.
9.一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶,前往B地,如表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x/时
0
1
2
2.5
余油量y/升
100
80
60
50
则y与x的函数关系式为
,自变量x的取值范围为
.
10.五一期间,小明一家自驾游去了离家200千米的某地,他们离家的距离y(千米)与汽车行驶时间x(小时)之间的关系为y=40x+60,当他们离目的地还有20千米时,汽车一共行驶的时间是
小时.
11.某物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)之间的图象如图所示,则v与t之间的函数关系式为
.
12.一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为
L.
13.空气中传播的速度y(m/s)与气温x(℃)之间的关系式为y=x+331;当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为
m.
14.甲、乙分别开车同时沿同一条路线从A地出发B地,已知A、B两地相距300km,他们出发1.5小时的时候乙车坏了,乙立即开始修车,甲车继续行驶,当甲第一次与乙相遇时,乙还在修车,乙修好车继续按原速前往B地.乙到达B地小时后,甲车到达B地.整个过程中,两人均保持各自的速度匀速行驶,甲、乙两人相距的路程y(千米)与甲出发的时间x(小时)之间的关系如图所示,则当乙车修好时,甲车距B地的路程为
千米.
15.一段平直的公路上有A,B,C三个城市,B城在A城和C城之间,一辆慢车从A城出发匀速开往B城,与此同时一辆快车从B城出发匀速开往C城.当慢车到达B城后即以倍原速匀速返回到A城,当快车到达C城后,休息了半小时后再提高原速的10%的速度匀速开往A城,如图是慢车出发后的时间t(小时)与两车之间的距离y(千米)之间的函数关系图,慢车出发6小时后,两车相距
千米.
16.10月期间,我市庆祝新中国成立70周年“祖国万岁”的主题灯光秀展示了两江四岸流光溢彩的壮美之景.周末,小明和小华相约一起乘轻轨去看灯光秀.已知小明家、轻轨站和小华家顺次分布在同一条笔直的公路上.小明、小华打算以各自的速度步行到轻轨站,小明出发3分钟后,小华从家里出发,走了两分钟,小华想起没带相机,立即掉头以原速的返回家中取相机,并在家中取停留5分钟,发现时间来不及便立即打车前住轻轨站,最终比小明早到2分钟.如图是两人之间的距离与小华出发时间之间的关系,则小明家离轻轨站的距离比小华家离轻轨站的距离少
米.
17.重庆某著名景区依托天然河道新开发了一款乘船体验项目.小明乘船由甲地顺流而下到乙地,然后由乙地逆流而上到丙地,然后靠岸乘车离开景点.若水流速度为2km/小时,船在静水中的速度为8km/小时.在整个乘船过程中,轮船与甲地相距的路程S(千米)与轮船出发的时间t(小时)之间的关系如图所示,甲乙两地间的距离为
千米.
18.一辆汽车开始行驶时,油箱内有油45升,如果每小时耗油6.5升,则这辆汽车油箱内剩余油量Q(升)与行驶时间t(小时)之间的关系式为
,且当t=4时,Q=
升.
19.为庆中国华诞70周年,国庆期间电影院推出了一系列爱国大片,其中《我和我的祖国》票房最高,学校为了对学生进行爱国主义教育,给每位学生发了张此片的电影票.明明在电影院门口发现忘记带电影票,遂边打电话给父亲边往家走,希望父亲能帮忙送来.1分钟后,父亲在家找到票开始往电影院走,再过8分钟两人相遇,父亲立即将票给明明,明明马上把速度提高到原来的倍跑向电影院,30秒后两人相距60米时,父亲才以不变的速度返家.两人的距离y(米)与明明出发的时间x(分)之间的关系如图所示,则当明明回到电影院门口时,父亲离家还有
米.
20.一条笔直的公路上顺次有A、B、C三地,小明驾车从B地出发匀速行驶前往A地,到达A地后停止,在小明出发的同时,小李驾车从B地出发匀速行驶前往A地,到达A地停留2小时后,调头按原速向C地行驶,若AB两地相距200千米,在行驶的过程中,两人之间的距离y(千米)与小李驾驶时间x(小时)之间的函数图象如图所示,则在他们出发后经过
小时相遇.
参考答案
1.解:由图象得:小玲骑车速度:7500÷30=250(米/分),
由函数图象得出,小丽在小玲5分后出发,12.5分时追上小玲,
设小丽去时的速度为v米/分,
(12.5﹣5)v=12.5×250,
v=,
则小丽回家的时间:=15(分钟),
当小丽刚好返回到阳光小区时,小玲离区疾病防控中心的距离为:250×(32﹣15﹣14.5)=625(米).
故答案为:625.
2.解:小敏一共走了:(1000﹣800)×2+1000=1400(米).
故答案为:1400.
3.解:观察图象知:甲跑64米用时8秒,速度为8m/s,
乙行驶52米用时8秒,速度为6.5m/s,
速度差为8﹣6.5=1.5m/s,
故答案为1.5.
4.解:(1)1.5﹣0.5=1(小时),
即修理所用的时间是1小时;
(2)由题意可知,乙从开始出发3小时追上甲.
故答案为:(1)1;(2)3.
5.解:由题,图可知甲走的是C路线,乙走的是D路线,
设s=kt+b①,
因为C过(0,0),(2,4)点,
所以代入①得:k=2,b=0,
所以sC=2t.
因为D过(2,4),(0,3)点,
代入①中得:k=,b=3,
所以sD=t+3,
当t=3时,sC﹣sD=6﹣=.
故答案为:
6.解:由图象可知,乙出发时,甲乙相距80km,2小时后,乙车追上甲.则说明乙每小时比甲快40km,则乙的速度为120km/h.①正确;
由图象第2﹣6小时,乙由相遇点到达B,用时4小时,每小时比甲快40km,则此时甲乙距离4×40=160km,则m=160,②正确;
当乙在B休息1h时,甲前进80km,则H点坐标为(7,80),③正确;
乙返回时,甲乙相距80km,到两车相遇用时80÷(120+80)=0.4小时,则n=6+1+0.4=7.4,④正确,
故答案为:①②③④.
7.解:由图象可得,
小李到达离家最远的地方的时间是14时,故(1)正确;
小李第一次休息时间是10时,故(2)正确;
11时到12时,小李骑了25﹣20=5(千米),故(3)正确;
返回时,小李的平均车速是30÷(16﹣14)=15(千米/小时),故(4)错误;
故答案为:(1)(2)(3).
8.解:由题意可得,
y=2000﹣×50=﹣5x+2500,
故答案为:y=﹣5x+2500.
9.解:设y与x之间的关系为一次函数,其函数表达式为y=kx+b,
将(0,100),(1,80)代入上式得,
,解得,
∴y=﹣20x+100;
100÷20=5,
∴0≤x≤5.
故答案为:y=﹣20x+100;0≤x≤5.
10.解:由题意可得,
当他们离目的地还有20千米时,则y=180,
当y=180时,180=40x+60,
解得,x=3,
即当他们离目的地还有20千米时,汽车一共行驶的时间是3小时,
故答案为:3.
11.解:设函数解析式为v=kt,
将点(2,5)代入得:5=2k,解得:k=,
∴v与t之间的函数解析式为v=(t≥0).
故答案为:v=(t≥0).
12.解:由图象可得,
每分钟的进水量为:20÷4=5(L),
每分钟的出水量为:5﹣(30﹣20)÷(12﹣4)=5﹣10÷8=5﹣1.25=3.75(L),
故答案为:3.75.
13.解:当x=22时,y=×22+331=344.2,
则当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为:344.2×5=1721(m),
故答案为:1721.
14.解:∵甲车速度==60千米/时,
∴甲车走完全程时间==5小时,
∴乙车速度=60+=120千米/时,
设乙车修了x小时,
由题意可得:120(﹣x)﹣60×=10,
∴x=,
∴当乙车修好时,甲车距B地的路程=300﹣60×(+)=110千米,
故答案为:110.
15.解:由题意可知A,B两地的距离为240千米;慢车用了4小时到达B地;
故慢车原速为:240÷4=60千米/时;
∴快车原速为:60+(320﹣240)÷2=100千米/时;
B,C两地的距离为:100×2=200千米,
∴慢车出发6小时后,两车相距为:(6﹣2﹣0.5)×100×(1+10%)﹣200﹣(6﹣4)×60×=25千米.
故答案为:25
16.解:由图象可得:小华到轻轨站时,小明家轻轨站的距离为240米,
∴小明的速度==120米/分,
∴小明家离轻轨站的距离=120×(12.5+3)=1860米,
设小华速度为x米/分,
∵小华家离轻轨站的距离=3120﹣[1860﹣120×(2+3+5+)]=2640米,
∵2640﹣1860=780米
∴小明家离轻轨站的距离比小华家离轻轨站的距离少780米,
故答案为:780.
17.解:根据图形可知甲、丙两地间的距离为2km.
(1)丙在甲地和乙地之间,设甲乙两地距离为x,
则,
解得:x=12.5.
(2)丙不在甲地和乙地之间,设甲乙两地距离为x,
则,
解得:x=10.
∴甲乙两地间的距离为12.5km或10km.
故答案为:12.5或10
18.解:依题意,得:Q=﹣6.5t+45.
当t=4时,Q=﹣6.5t+45=19.
故答案为:Q=﹣6.5t+45;19.
19.解:由题意可得,
返回时明明的速度为:(米/分),
∴返回前明明的速度为:120×=90(米/分),
设爸爸的速度为x米/分钟,根据题意得,
8(90+x)=1450﹣90×1,
解得x=80,
∴爸爸的速度为80米/分钟,
明明从电影院到相遇所走路程为:90×9=810(米),
爸爸从家到相遇所走路程为:80×8=640(米),
明明返回时所用时间为:,
此时爸爸走了:80×()=500(米),
∴当明明回到电影院门口时,父亲与家的距离为:640﹣500=140(米).
故答案为:140
20.解:∵最终两车相距400千米,
∴A、C两地相距400千米.
小李的速度为(200+400)÷(8﹣2)=100(千米/小时),
小李从B到达A地的时间为200÷100=2(小时),
小明的速度为(200﹣120)÷3=40(千米/小时),
小李从A地返回时,两车的间距为200﹣40×4=40(千米),
两车相遇的时间为4+=4(小时)
故答案为:4.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
