苏科版七年级数学上册6章 平面图形的认识(一)6.1-6.3 阶段 培优训练卷(Word版 有答案)
文档属性
| 名称 | 苏科版七年级数学上册6章 平面图形的认识(一)6.1-6.3 阶段 培优训练卷(Word版 有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 194.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览



文档简介
2020-2021苏科版七年级数学上册6章平面图形的认识(一)6.1-6.3阶段
培优训练卷
一、选择题
1、图中给出的直线、射线、线段,根据各自的性质,能相交的是
(
)
2、下列说法:①一根拉的很紧的细线就是直线;②直线的一半是射线;
③一直线上的任意一点把这条直线分成两条射线;④经过两点只有一条线段;
⑤在所有连接两点的线中,线段最短,其中正确的个数是
(
)
A.1个
B.2个
C.3个
D.4个
3、图中共有线段( )
A.4条
B.6条
C.8条
D.10条
4、如果点C在AB上,下列表达式:①AC=AB;②AB=2BC;③AC=BC;④AC+BC=AB中,能表示C是AB中点的有
(
)
A.1个
B.2个
C.3个
D.4个
5、如图,直线AB,CD相交于点O,已知∠AOC=80°,∠BOE:∠EOD=3:2,则∠AOE的度数是( )
A.100°
B.116°
C.120°
D.132°
6、如图,C为线段AD上一点,点B为CD的中点,且AD=9,BD=2.若点E在直线AD上,且EA=1,则BE的长为( )
A.4
B.6或8
C.6
D.8
7、如图,下列表示角的方法错误的是(
)
A.∠1与∠AOB表示同一个角
B.∠AOC可用么O来表示
C.图中共有三个角∠AOB、∠AOC、∠BOC
D.∠β表示的是∠BOC
8、已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是( )
A.20°或50°
B.20°或60°
C.30°或50°
D.30°或60°
9、已知∠A=115°,∠B是∠A的补角,则∠B的余角的度数是( )
A.65°
B.115°
C.15°
D.25°
10、下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,②
B.①,②,③
C.③,④,②
D.③,④
11、下列说法中,正确的是( ).
①射线AB和射线BA是同一条射线;
②若AB=BC,则点B为线段AC的中点;
③同角的补角相等;
④点C在线段AB上,M,N分别是线段AC,CB的中点.
若MN=5,则线段AB=10.
A.①②?????
B.②③??????
C.②④??????
D.③④
12、下列说法:①一个角的补角大于这个角;②小于平角的角是钝角;③同角或等角的余角相等;
④若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为补角,其中正确的说法有( )
A.4个
B.3个
C.2个
D.1个
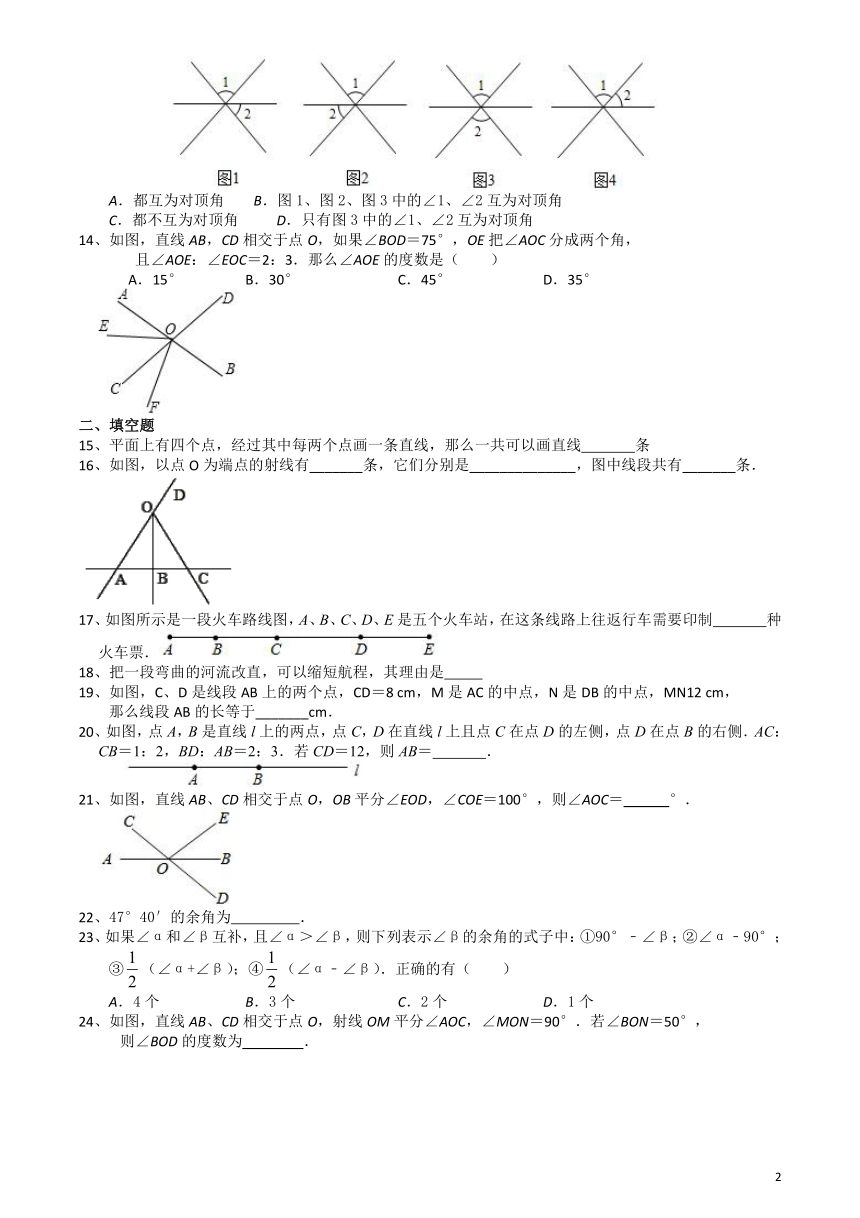
13、下面四个图形中∠1与∠2为互为对顶角的说法正确的是( )
A.都互为对顶角
B.图1、图2、图3中的∠1、∠2互为对顶角
C.都不互为对顶角
D.只有图3中的∠1、∠2互为对顶角
14、如图,直线AB,CD相交于点O,如果∠BOD=75°,OE把∠AOC分成两个角,
且∠AOE:∠EOC=2:3.那么∠AOE的度数是( )
A.15°
B.30°
C.45°
D.35°
二、填空题
15、平面上有四个点,经过其中每两个点画一条直线,那么一共可以画直线
条
16、如图,以点O为端点的射线有_______条,它们分别是______________,图中线段共有_______条.
17、如图所示是一段火车路线图,A、B、C、D、E是五个火车站,在这条线路上往返行车需要印制
种火车票.
18、把一段弯曲的河流改直,可以缩短航程,其理由是
19、如图,C、D是线段AB上的两个点,CD=8
cm,M是AC的中点,N是DB的中点,MN12
cm,
那么线段AB的长等于_______cm.
20、如图,点A,B是直线l上的两点,点C,D在直线l上且点C在点D的左侧,点D在点B的右侧.AC:CB=1:2,BD:AB=2:3.若CD=12,则AB=
.
21、如图,直线AB、CD相交于点O,OB平分∠EOD,∠COE=100°,则∠AOC=
°.
22、47°40′的余角为
.
23、如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有( )
A.4个
B.3个
C.2个
D.1个
24、如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠BON=50°,
则∠BOD的度数为
.
三、解答题
25、已知道四点A、B、C、D,按要求画图.
(1)画直线AB、CD交于E点;
(2)画线段AC、BD交于点F;
(3)作射线BC.
26、如图,线段AB=8
cm,C是线段AB上一点,AC=3.2
cm,M是AB的中点,N是AC的中点,
求线段MN的长.
27、如图:A、B、C、D四点在同一直线上.
(1)若AB=CD.
①比较线段的大小:AC
BD(填“>”、“=”或“<”);
②若BC=AC,且AC=12cm,则AD的长为
cm;
(2)若线段AD被点B、C分成了3:4:5三部分,且AB的中点M和CD的中点N之间的距离是16cm,求AD的长.
28、如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.
(1)若∠AOE=15°,求∠FOC的度数;
(2)若∠AOB=86°,求∠DOE的度数.
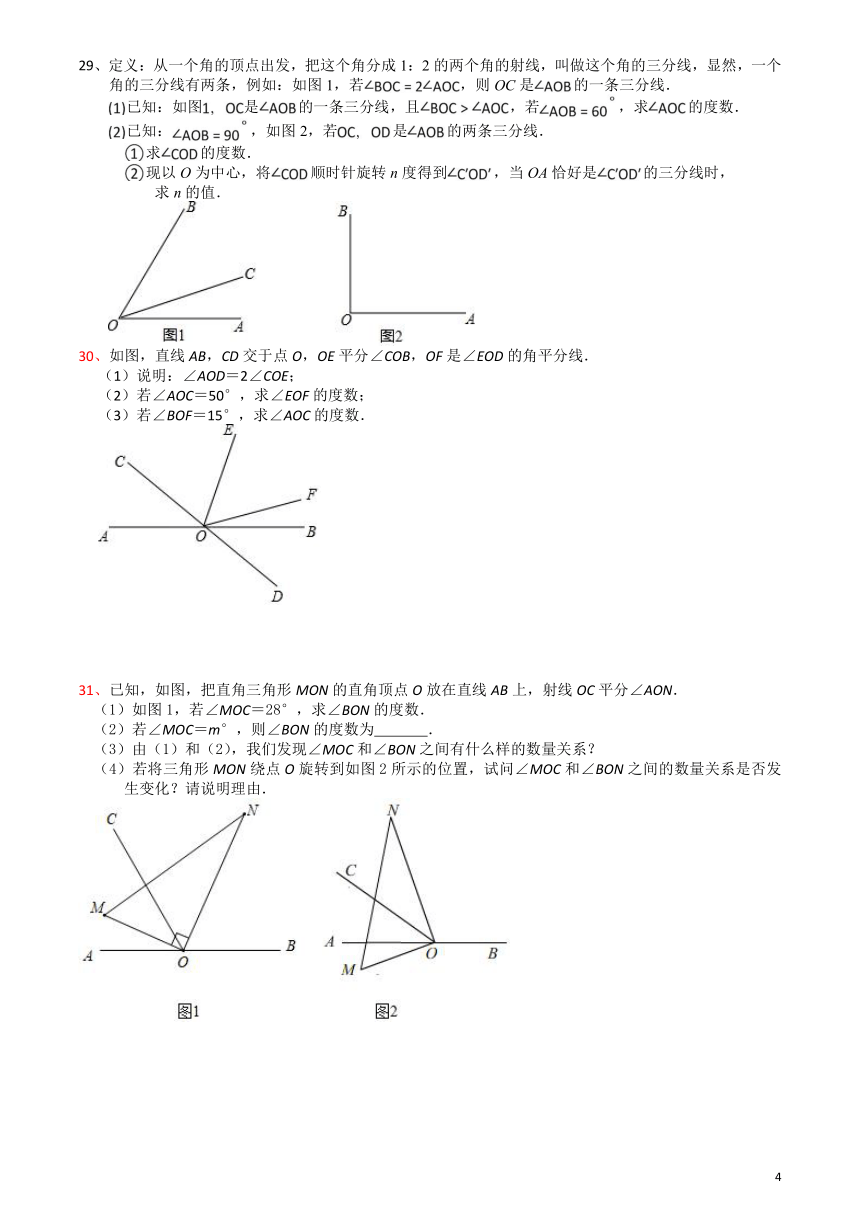
29、定义:从一个角的顶点出发,把这个角分成1:2的两个角的射线,叫做这个角的三分线,显然,一个角的三分线有两条,例如:如图1,若,则OC是的一条三分线.
已知:如图是的一条三分线,且,若,求的度数.
已知:,如图2,若是的两条三分线.
求的度数.
现以O为中心,将顺时针旋转n度得到,当OA恰好是的三分线时,
求n的值.
30、如图,直线AB,CD交于点O,OE平分∠COB,OF是∠EOD的角平分线.
(1)说明:∠AOD=2∠COE;
(2)若∠AOC=50°,求∠EOF的度数;
(3)若∠BOF=15°,求∠AOC的度数.
31、已知,如图,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数.
(2)若∠MOC=m°,则∠BON的度数为
.
(3)由(1)和(2),我们发现∠MOC和∠BON之间有什么样的数量关系?
(4)若将三角形MON绕点O旋转到如图2所示的位置,试问∠MOC和∠BON之间的数量关系是否发生变化?请说明理由.
2020-2021苏科版七年级数学上册6章平面图形的认识(一)6.1-6.3阶段
培优训练卷(答案)
一、选择题
1、图中给出的直线、射线、线段,根据各自的性质,能相交的是
(
)
【解析】A.射线延伸后两直线不能相交,故本选项错误;
B.直线延伸后两直线不能相交,故本选项错误;
C.射线和直线延伸后两直线不能相交,故本选项错误;
D.射线延伸后两直线能相交,故本选项正确;
故选D
2、下列说法:①一根拉的很紧的细线就是直线;②直线的一半是射线;
③一直线上的任意一点把这条直线分成两条射线;④经过两点只有一条线段;
⑤在所有连接两点的线中,线段最短,其中正确的个数是
(
)
A.1个
B.2个
C.3个
D.4个
【解析】①错误,细线始终有端点,所以它是线段.实际生活中除了光、声音之类的,不存在射线,更不用说直线;
②错误,直线可以无限延长,所以没有一半;
③正确,射线定义:只有一个端点,另一端无限延长,任意的一点可看作两条射线分别的端点;
④正确,过两点作一条直线;
⑤正确,两点之间线段最短.
故选C
3、图中共有线段( )
A.4条
B.6条
C.8条
D.10条
解:图中的线段有AC、AD、AE、AB;CD、CE、CB;DE、DB;EB;共10条,
故选:D.
4、如果点C在AB上,下列表达式:①AC=AB;②AB=2BC;③AC=BC;④AC+BC=AB中,能表示C是AB中点的有
(
)
A.1个
B.2个
C.3个
D.4个
【解析】如图,能表示点C是线段AB的中点的是AB=BC,AC=BC,
而AC=AB和AC+BC=AB都不能表示C是线段AB的中点,即正确的有②③两个.
故选B.
5、如图,直线AB,CD相交于点O,已知∠AOC=80°,∠BOE:∠EOD=3:2,则∠AOE的度数是( )
A.100°
B.116°
C.120°
D.132°
【解析】∵∠AOC=80°,∴∠DOB=80°,∠AOD=100°,
∵∠BOE:∠EOD=3:2,∴∠DOE=80°×=32°,
∴∠AOE=100°+32°=132°,故选:D.
6、如图,C为线段AD上一点,点B为CD的中点,且AD=9,BD=2.若点E在直线AD上,且EA=1,则BE的长为( )
A.4
B.6或8
C.6
D.8
解:若E在线段DA的延长线,如图1,
∵EA=1,AD=9,∴ED=EA+AD=1+9=10,
∵BD=2,∴BE=ED﹣BD=10﹣2=8,
若E线段AD上,如图2,EA=1,AD=9,∴ED=AD﹣EA=9﹣1=8,
∵BD=2,∴BE=ED﹣BD=8﹣2=6,
综上所述,BE的长为8或6.
故选:B.
7、如图,下列表示角的方法错误的是(
)
A.∠1与∠AOB表示同一个角
B.∠AOC可用么O来表示
C.图中共有三个角∠AOB、∠AOC、∠BOC
D.∠β表示的是∠BOC
【解析】以点O为顶点的角有3个,因此不能用单独的顶点字母表示一个角,所以B项错误.
8、已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是( C )
A.20°或50°
B.20°或60°
C.30°或50°
D.30°或60°
9、已知∠A=115°,∠B是∠A的补角,则∠B的余角的度数是( )
A.65°
B.115°
C.15°
D.25°
【解答】解:∠A的补角∠B的度数是:180°﹣115°=65°,
则余角是90°﹣65°=25°.
故选:D.
10、下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,②
B.①,②,③
C.③,④,②
D.③,④
【解析】①已知∠A=40°,则∠A的余角是50°,原说法正确;
②若∠1+∠2=90°,则∠1和∠2互为余角,原说法正确;
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3不能互为补角,原说法错误;
④一个角的补角不一定是钝角,原说法错误.
说法正确的是①②,
故选A.
11、下列说法中,正确的是(D ).
①射线AB和射线BA是同一条射线;
②若AB=BC,则点B为线段AC的中点;
③同角的补角相等;
④点C在线段AB上,M,N分别是线段AC,CB的中点.
若MN=5,则线段AB=10.
A.①②?????
B.②③??????
C.②④??????
D.③④
12、下列说法:①一个角的补角大于这个角;②小于平角的角是钝角;③同角或等角的余角相等;
④若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为补角,其中正确的说法有( )
A.4个
B.3个
C.2个
D.1个
【解答】解:①已知∠A=140°,则∠A的补角=40°,原来的说法错误;
②大于直角小于平角的角是钝角,原来的说法错误;
③同角或等角的余角相等是正确的;
④和为180度的两个角互为补角,原来的说法错误.
故其中正确的说法有1个.
故选:D.
13、下面四个图形中∠1与∠2为互为对顶角的说法正确的是( )
A.都互为对顶角
B.图1、图2、图3中的∠1、∠2互为对顶角
C.都不互为对顶角
D.只有图3中的∠1、∠2互为对顶角
【解析】根据对顶角的定义可知:只有图3中的∠1、∠2互为对顶角,
故选D.
14、如图,直线AB,CD相交于点O,如果∠BOD=75°,OE把∠AOC分成两个角,
且∠AOE:∠EOC=2:3.那么∠AOE的度数是( )
A.15°
B.30°
C.45°
D.35°
【解析】∵∠BOD=75°,∴∠AOC=75°,
∵∠AOE:∠EOC=2:3,∴设∠AOE=2x°,∠EOC=3x°,则2x+3x=75,
解得:x=15,∴∠AOE=30°,故选:B.
二、填空题
15、平面上有四个点,经过其中每两个点画一条直线,那么一共可以画直线
条
解:①当四点共线时,则经过每两个点画一条直线,那么共可以画直线1条;
②当只有三点共线时,则经过每两个点画一条直线,那么共可以画直线4条;
③当每三点不共线时,则经过每两个点画一条直线,那么共可以画直线6条.
故答案为:1或4或6.
16、如图,以点O为端点的射线有_______条,它们分别是______________,图中线段共有_______条.
【解析】以O为端点的射线有
OA、OB、OC、OD,共四条;
一共有八条线段,分别是
OD、OA、OB、OC、AD、AB、AC、BC.
答案:
4;
射线OA、射线OB,、射线OC,、射线OD;
8.
17、如图所示是一段火车路线图,A、B、C、D、E是五个火车站,在这条线路上往返行车需要印制
种火车票.
解:图中线段有:AB、AC、AD、AE,BC、BD、BE,CD、CE、DE,
共10条,
∵每条线段应印2种车票,∴共需印10×2=20种车票.
故答案为:20.
18、把一段弯曲的河流改直,可以缩短航程,其理由是
解:把一段弯曲的河流改直,可以缩短航程,其理由是两点之间,线段最短,
故答案为:两点之间,线段最短.
19、如图,C、D是线段AB上的两个点,CD=8
cm,M是AC的中点,N是DB的中点,MN12
cm,
那么线段AB的长等于_______cm.
【解析】∵M是AC的中点,N是DB的中点,∴AM=MC,BN=DN,
∴AM+BN=MC+DN=MN-CD=4cm,∴AB=AM+BN+CD=12cm.
20、如图,点A,B是直线l上的两点,点C,D在直线l上且点C在点D的左侧,点D在点B的右侧.AC:CB=1:2,BD:AB=2:3.若CD=12,则AB=
.
解:对C点的位置分情况讨论如下:
①C点在A点的左边,∵AC:CB=1:2,BD:AB=2:3,
假设AC=3k,则AB=3k,BD=2k,∴CD=3k+3k+2k=8k,
∵CD=12,∴k=1.5,∴AB=4.5;
②C点在线段AB上,∵AC:CB=1:2,BD:AB=2:3,
假设AC=k,则CB=2k,BD=2k,∴CD=CB+BD=4k,
∵CD=12,∴k=3,∴AB=AC+CB=3k=9;
③C点在B点后,不符合题意,舍去;∴综上所述,AB=4.5或9.
21、如图,直线AB、CD相交于点O,OB平分∠EOD,∠COE=100°,则∠AOC=
°.
【解析】∵∠COE=100°,∴∠DOE=80°,
∵OB平分∠EOD,∴∠BOD=40°,∴∠AOC=40°,故答案为:40.
22、47°40′的余角为
.
【解析】47°40′的余角的度数为:
90°﹣47°40′=42°20′.
故答案为42°20′.
23、如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有( )
A.4个
B.3个
C.2个
D.1个
【解析】∵∠α和∠β互补,∴∠α+∠β=180°.因为90°﹣∠β+∠β=90°,所以①正确;
又∠α﹣90°+∠β=∠α+∠β﹣90°=180°﹣90°=90°,②也正确;
(∠α+∠β)+∠β=×180°+∠β=90°+∠β≠90°,所以③错误;
(∠α﹣∠β)+∠β=(∠α+∠β)=×180°=90°,所以④正确.
综上可知,①②④均正确.
24、如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠BON=50°,
则∠BOD的度数为
.
【解析】∵∠MON=90°.∠BON=50°,∴∠AOM=90°﹣50°′=40°,
∵射线OM平分∠AOC,∴∠AOC=40°×2=80°,∴∠BOD=∠AOC=80°.
故答案为:80°.
三、解答题
25、已知道四点A、B、C、D,按要求画图.
(1)画直线AB、CD交于E点;
(2)画线段AC、BD交于点F;
(3)作射线BC.
解:(1)
(2)
(3)
26、如图,线段AB=8
cm,C是线段AB上一点,AC=3.2
cm,M是AB的中点,N是AC的中点,
求线段MN的长.
解:由AB=8,M是AB的中点,所以AM=4,
又AC=3.2,所以CM=0.8cm;
因为N是AC的中点,所以NC=1.6,
所以MN=NC+CM=2.4cm.
27、如图:A、B、C、D四点在同一直线上.
(1)若AB=CD.
①比较线段的大小:AC
BD(填“>”、“=”或“<”);
②若BC=AC,且AC=12cm,则AD的长为
cm;
(2)若线段AD被点B、C分成了3:4:5三部分,且AB的中点M和CD的中点N之间的距离是16cm,求AD的长.
解:(1)①∵AB=CD,∴AB+BC=CD+BC,即,AC=BD,故答案为:=;
②∵BC=AC,且AC=12cm,∴BC=×12=9(cm),
∴AB=CD=AC﹣BC=12﹣9=3(cm),∴AD=AC+CD=12+3=15(cm),故答案为:15;
(2)如图,
设每份为x,则AB=3x,BC=4x,CD=5x,AD=12x,
∵M是AB的中点,点N是CD的中点N,∴AM=BM=x,CN=DN=x,
又∵MN=16,
∴x+4x+x=16,
解得,x=2,
∴AD=12x=24(cm),
答:AD的长为24cm.
28、如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.
(1)若∠AOE=15°,求∠FOC的度数;
(2)若∠AOB=86°,求∠DOE的度数.
解:(1)∵∠AOE=15°,OE平分∠AOC,∴∠AOC=2×15°=30°,
∵点O是直线FA上一点,∴∠FOC=180°﹣30°=150°.
(2)∵OE平分∠AOC,OD平分∠BOC,∴∠EOC=∠AOC,∠DOC=∠BOC,
∴∠DOE=∠AOC+∠BOC=∠AOB=×86°=43°.
29、定义:从一个角的顶点出发,把这个角分成1:2的两个角的射线,叫做这个角的三分线,显然,一个角的三分线有两条,例如:如图1,若,则OC是的一条三分线.
已知:如图是的一条三分线,且,若,求的度数.
已知:,如图2,若是的两条三分线.
求的度数.
现以O为中心,将顺时针旋转n度得到,当OA恰好是的三分线时,
求n的值.
解:如图是的一条三分线,且,,
又,;
如图是的两条三分线,;
分两种情况:
当OA是的三分线,且
∠AOC{{'}}'/>时,,
,;
当OA是的三分线,且时,,
,;
综上所述,或.??
30、如图,直线AB,CD交于点O,OE平分∠COB,OF是∠EOD的角平分线.
(1)说明:∠AOD=2∠COE;
(2)若∠AOC=50°,求∠EOF的度数;
(3)若∠BOF=15°,求∠AOC的度数.
【解析】(1)∵OE平分∠COB,∴∠COE∠COB,
∵∠AOD=∠COB,∴∠AOD=2∠COE;
(2)∵∠AOC=50°,∴∠BOC=180°﹣50°=130°,∴∠EOC∠BOC=65°,
∴∠DOE=180°﹣∠EOC=180°﹣65°=115°,
∵OF平分∠DOE,∴∠EOF∠DOC=57.5°;
(3)设∠AOC=∠BOD=α,则∠DOF=α+15°,∴∠EOF=∠DOF=α+15°,
∴∠EOB=∠EOF+∠BOF=α+30°,∴∠COB=2∠EOB=2α+60°,
而∠COB+∠BOD=180°,即,3α+60°=180°,解得,α=40°,即,∠AOC=40°.
31、已知,如图,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数.
(2)若∠MOC=m°,则∠BON的度数为
.
(3)由(1)和(2),我们发现∠MOC和∠BON之间有什么样的数量关系?
(4)若将三角形MON绕点O旋转到如图2所示的位置,试问∠MOC和∠BON之间的数量关系是否发生变化?请说明理由.
【解析】(1)如图1,∵∠MOC=28°,∠MON=90°,∴∠NOC=90°﹣28°=62°,
又∵OC平分∠AON,∴∠AOC=∠NOC=62°,
∴∠BON=180°﹣2∠NOC=180°﹣62°×2=56°,
(2)如图1,∵∠MOC=m°,∠MON=90°,∴∠NOC=90°﹣m°=(90﹣m)°,
又∵OC平分∠AON,∴∠AOC=∠NOC=(90﹣m)°,
∴∠BON=180°﹣2∠NOC=180°﹣(90﹣m)°×2=2m°,
故答案为2m°;
(3)由(1)和(2)可得:∠BON=2∠MOC;
(4)∠MOC和∠BON之间的数量关系不发生变化,
如图2,∵OC平分∠AON,∴∠AOC=∠NOC,
∵∠MON=90°,∴∠AOC=∠NOC=90°﹣∠MOC,
∴∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC,
即:∴∠BON=2∠MOC.
培优训练卷
一、选择题
1、图中给出的直线、射线、线段,根据各自的性质,能相交的是
(
)
2、下列说法:①一根拉的很紧的细线就是直线;②直线的一半是射线;
③一直线上的任意一点把这条直线分成两条射线;④经过两点只有一条线段;
⑤在所有连接两点的线中,线段最短,其中正确的个数是
(
)
A.1个
B.2个
C.3个
D.4个
3、图中共有线段( )
A.4条
B.6条
C.8条
D.10条
4、如果点C在AB上,下列表达式:①AC=AB;②AB=2BC;③AC=BC;④AC+BC=AB中,能表示C是AB中点的有
(
)
A.1个
B.2个
C.3个
D.4个
5、如图,直线AB,CD相交于点O,已知∠AOC=80°,∠BOE:∠EOD=3:2,则∠AOE的度数是( )
A.100°
B.116°
C.120°
D.132°
6、如图,C为线段AD上一点,点B为CD的中点,且AD=9,BD=2.若点E在直线AD上,且EA=1,则BE的长为( )
A.4
B.6或8
C.6
D.8
7、如图,下列表示角的方法错误的是(
)
A.∠1与∠AOB表示同一个角
B.∠AOC可用么O来表示
C.图中共有三个角∠AOB、∠AOC、∠BOC
D.∠β表示的是∠BOC
8、已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是( )
A.20°或50°
B.20°或60°
C.30°或50°
D.30°或60°
9、已知∠A=115°,∠B是∠A的补角,则∠B的余角的度数是( )
A.65°
B.115°
C.15°
D.25°
10、下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,②
B.①,②,③
C.③,④,②
D.③,④
11、下列说法中,正确的是( ).
①射线AB和射线BA是同一条射线;
②若AB=BC,则点B为线段AC的中点;
③同角的补角相等;
④点C在线段AB上,M,N分别是线段AC,CB的中点.
若MN=5,则线段AB=10.
A.①②?????
B.②③??????
C.②④??????
D.③④
12、下列说法:①一个角的补角大于这个角;②小于平角的角是钝角;③同角或等角的余角相等;
④若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为补角,其中正确的说法有( )
A.4个
B.3个
C.2个
D.1个
13、下面四个图形中∠1与∠2为互为对顶角的说法正确的是( )
A.都互为对顶角
B.图1、图2、图3中的∠1、∠2互为对顶角
C.都不互为对顶角
D.只有图3中的∠1、∠2互为对顶角
14、如图,直线AB,CD相交于点O,如果∠BOD=75°,OE把∠AOC分成两个角,
且∠AOE:∠EOC=2:3.那么∠AOE的度数是( )
A.15°
B.30°
C.45°
D.35°
二、填空题
15、平面上有四个点,经过其中每两个点画一条直线,那么一共可以画直线
条
16、如图,以点O为端点的射线有_______条,它们分别是______________,图中线段共有_______条.
17、如图所示是一段火车路线图,A、B、C、D、E是五个火车站,在这条线路上往返行车需要印制
种火车票.
18、把一段弯曲的河流改直,可以缩短航程,其理由是
19、如图,C、D是线段AB上的两个点,CD=8
cm,M是AC的中点,N是DB的中点,MN12
cm,
那么线段AB的长等于_______cm.
20、如图,点A,B是直线l上的两点,点C,D在直线l上且点C在点D的左侧,点D在点B的右侧.AC:CB=1:2,BD:AB=2:3.若CD=12,则AB=
.
21、如图,直线AB、CD相交于点O,OB平分∠EOD,∠COE=100°,则∠AOC=
°.
22、47°40′的余角为
.
23、如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有( )
A.4个
B.3个
C.2个
D.1个
24、如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠BON=50°,
则∠BOD的度数为
.
三、解答题
25、已知道四点A、B、C、D,按要求画图.
(1)画直线AB、CD交于E点;
(2)画线段AC、BD交于点F;
(3)作射线BC.
26、如图,线段AB=8
cm,C是线段AB上一点,AC=3.2
cm,M是AB的中点,N是AC的中点,
求线段MN的长.
27、如图:A、B、C、D四点在同一直线上.
(1)若AB=CD.
①比较线段的大小:AC
BD(填“>”、“=”或“<”);
②若BC=AC,且AC=12cm,则AD的长为
cm;
(2)若线段AD被点B、C分成了3:4:5三部分,且AB的中点M和CD的中点N之间的距离是16cm,求AD的长.
28、如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.
(1)若∠AOE=15°,求∠FOC的度数;
(2)若∠AOB=86°,求∠DOE的度数.
29、定义:从一个角的顶点出发,把这个角分成1:2的两个角的射线,叫做这个角的三分线,显然,一个角的三分线有两条,例如:如图1,若,则OC是的一条三分线.
已知:如图是的一条三分线,且,若,求的度数.
已知:,如图2,若是的两条三分线.
求的度数.
现以O为中心,将顺时针旋转n度得到,当OA恰好是的三分线时,
求n的值.
30、如图,直线AB,CD交于点O,OE平分∠COB,OF是∠EOD的角平分线.
(1)说明:∠AOD=2∠COE;
(2)若∠AOC=50°,求∠EOF的度数;
(3)若∠BOF=15°,求∠AOC的度数.
31、已知,如图,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数.
(2)若∠MOC=m°,则∠BON的度数为
.
(3)由(1)和(2),我们发现∠MOC和∠BON之间有什么样的数量关系?
(4)若将三角形MON绕点O旋转到如图2所示的位置,试问∠MOC和∠BON之间的数量关系是否发生变化?请说明理由.
2020-2021苏科版七年级数学上册6章平面图形的认识(一)6.1-6.3阶段
培优训练卷(答案)
一、选择题
1、图中给出的直线、射线、线段,根据各自的性质,能相交的是
(
)
【解析】A.射线延伸后两直线不能相交,故本选项错误;
B.直线延伸后两直线不能相交,故本选项错误;
C.射线和直线延伸后两直线不能相交,故本选项错误;
D.射线延伸后两直线能相交,故本选项正确;
故选D
2、下列说法:①一根拉的很紧的细线就是直线;②直线的一半是射线;
③一直线上的任意一点把这条直线分成两条射线;④经过两点只有一条线段;
⑤在所有连接两点的线中,线段最短,其中正确的个数是
(
)
A.1个
B.2个
C.3个
D.4个
【解析】①错误,细线始终有端点,所以它是线段.实际生活中除了光、声音之类的,不存在射线,更不用说直线;
②错误,直线可以无限延长,所以没有一半;
③正确,射线定义:只有一个端点,另一端无限延长,任意的一点可看作两条射线分别的端点;
④正确,过两点作一条直线;
⑤正确,两点之间线段最短.
故选C
3、图中共有线段( )
A.4条
B.6条
C.8条
D.10条
解:图中的线段有AC、AD、AE、AB;CD、CE、CB;DE、DB;EB;共10条,
故选:D.
4、如果点C在AB上,下列表达式:①AC=AB;②AB=2BC;③AC=BC;④AC+BC=AB中,能表示C是AB中点的有
(
)
A.1个
B.2个
C.3个
D.4个
【解析】如图,能表示点C是线段AB的中点的是AB=BC,AC=BC,
而AC=AB和AC+BC=AB都不能表示C是线段AB的中点,即正确的有②③两个.
故选B.
5、如图,直线AB,CD相交于点O,已知∠AOC=80°,∠BOE:∠EOD=3:2,则∠AOE的度数是( )
A.100°
B.116°
C.120°
D.132°
【解析】∵∠AOC=80°,∴∠DOB=80°,∠AOD=100°,
∵∠BOE:∠EOD=3:2,∴∠DOE=80°×=32°,
∴∠AOE=100°+32°=132°,故选:D.
6、如图,C为线段AD上一点,点B为CD的中点,且AD=9,BD=2.若点E在直线AD上,且EA=1,则BE的长为( )
A.4
B.6或8
C.6
D.8
解:若E在线段DA的延长线,如图1,
∵EA=1,AD=9,∴ED=EA+AD=1+9=10,
∵BD=2,∴BE=ED﹣BD=10﹣2=8,
若E线段AD上,如图2,EA=1,AD=9,∴ED=AD﹣EA=9﹣1=8,
∵BD=2,∴BE=ED﹣BD=8﹣2=6,
综上所述,BE的长为8或6.
故选:B.
7、如图,下列表示角的方法错误的是(
)
A.∠1与∠AOB表示同一个角
B.∠AOC可用么O来表示
C.图中共有三个角∠AOB、∠AOC、∠BOC
D.∠β表示的是∠BOC
【解析】以点O为顶点的角有3个,因此不能用单独的顶点字母表示一个角,所以B项错误.
8、已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是( C )
A.20°或50°
B.20°或60°
C.30°或50°
D.30°或60°
9、已知∠A=115°,∠B是∠A的补角,则∠B的余角的度数是( )
A.65°
B.115°
C.15°
D.25°
【解答】解:∠A的补角∠B的度数是:180°﹣115°=65°,
则余角是90°﹣65°=25°.
故选:D.
10、下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,②
B.①,②,③
C.③,④,②
D.③,④
【解析】①已知∠A=40°,则∠A的余角是50°,原说法正确;
②若∠1+∠2=90°,则∠1和∠2互为余角,原说法正确;
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3不能互为补角,原说法错误;
④一个角的补角不一定是钝角,原说法错误.
说法正确的是①②,
故选A.
11、下列说法中,正确的是(D ).
①射线AB和射线BA是同一条射线;
②若AB=BC,则点B为线段AC的中点;
③同角的补角相等;
④点C在线段AB上,M,N分别是线段AC,CB的中点.
若MN=5,则线段AB=10.
A.①②?????
B.②③??????
C.②④??????
D.③④
12、下列说法:①一个角的补角大于这个角;②小于平角的角是钝角;③同角或等角的余角相等;
④若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为补角,其中正确的说法有( )
A.4个
B.3个
C.2个
D.1个
【解答】解:①已知∠A=140°,则∠A的补角=40°,原来的说法错误;
②大于直角小于平角的角是钝角,原来的说法错误;
③同角或等角的余角相等是正确的;
④和为180度的两个角互为补角,原来的说法错误.
故其中正确的说法有1个.
故选:D.
13、下面四个图形中∠1与∠2为互为对顶角的说法正确的是( )
A.都互为对顶角
B.图1、图2、图3中的∠1、∠2互为对顶角
C.都不互为对顶角
D.只有图3中的∠1、∠2互为对顶角
【解析】根据对顶角的定义可知:只有图3中的∠1、∠2互为对顶角,
故选D.
14、如图,直线AB,CD相交于点O,如果∠BOD=75°,OE把∠AOC分成两个角,
且∠AOE:∠EOC=2:3.那么∠AOE的度数是( )
A.15°
B.30°
C.45°
D.35°
【解析】∵∠BOD=75°,∴∠AOC=75°,
∵∠AOE:∠EOC=2:3,∴设∠AOE=2x°,∠EOC=3x°,则2x+3x=75,
解得:x=15,∴∠AOE=30°,故选:B.
二、填空题
15、平面上有四个点,经过其中每两个点画一条直线,那么一共可以画直线
条
解:①当四点共线时,则经过每两个点画一条直线,那么共可以画直线1条;
②当只有三点共线时,则经过每两个点画一条直线,那么共可以画直线4条;
③当每三点不共线时,则经过每两个点画一条直线,那么共可以画直线6条.
故答案为:1或4或6.
16、如图,以点O为端点的射线有_______条,它们分别是______________,图中线段共有_______条.
【解析】以O为端点的射线有
OA、OB、OC、OD,共四条;
一共有八条线段,分别是
OD、OA、OB、OC、AD、AB、AC、BC.
答案:
4;
射线OA、射线OB,、射线OC,、射线OD;
8.
17、如图所示是一段火车路线图,A、B、C、D、E是五个火车站,在这条线路上往返行车需要印制
种火车票.
解:图中线段有:AB、AC、AD、AE,BC、BD、BE,CD、CE、DE,
共10条,
∵每条线段应印2种车票,∴共需印10×2=20种车票.
故答案为:20.
18、把一段弯曲的河流改直,可以缩短航程,其理由是
解:把一段弯曲的河流改直,可以缩短航程,其理由是两点之间,线段最短,
故答案为:两点之间,线段最短.
19、如图,C、D是线段AB上的两个点,CD=8
cm,M是AC的中点,N是DB的中点,MN12
cm,
那么线段AB的长等于_______cm.
【解析】∵M是AC的中点,N是DB的中点,∴AM=MC,BN=DN,
∴AM+BN=MC+DN=MN-CD=4cm,∴AB=AM+BN+CD=12cm.
20、如图,点A,B是直线l上的两点,点C,D在直线l上且点C在点D的左侧,点D在点B的右侧.AC:CB=1:2,BD:AB=2:3.若CD=12,则AB=
.
解:对C点的位置分情况讨论如下:
①C点在A点的左边,∵AC:CB=1:2,BD:AB=2:3,
假设AC=3k,则AB=3k,BD=2k,∴CD=3k+3k+2k=8k,
∵CD=12,∴k=1.5,∴AB=4.5;
②C点在线段AB上,∵AC:CB=1:2,BD:AB=2:3,
假设AC=k,则CB=2k,BD=2k,∴CD=CB+BD=4k,
∵CD=12,∴k=3,∴AB=AC+CB=3k=9;
③C点在B点后,不符合题意,舍去;∴综上所述,AB=4.5或9.
21、如图,直线AB、CD相交于点O,OB平分∠EOD,∠COE=100°,则∠AOC=
°.
【解析】∵∠COE=100°,∴∠DOE=80°,
∵OB平分∠EOD,∴∠BOD=40°,∴∠AOC=40°,故答案为:40.
22、47°40′的余角为
.
【解析】47°40′的余角的度数为:
90°﹣47°40′=42°20′.
故答案为42°20′.
23、如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有( )
A.4个
B.3个
C.2个
D.1个
【解析】∵∠α和∠β互补,∴∠α+∠β=180°.因为90°﹣∠β+∠β=90°,所以①正确;
又∠α﹣90°+∠β=∠α+∠β﹣90°=180°﹣90°=90°,②也正确;
(∠α+∠β)+∠β=×180°+∠β=90°+∠β≠90°,所以③错误;
(∠α﹣∠β)+∠β=(∠α+∠β)=×180°=90°,所以④正确.
综上可知,①②④均正确.
24、如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠BON=50°,
则∠BOD的度数为
.
【解析】∵∠MON=90°.∠BON=50°,∴∠AOM=90°﹣50°′=40°,
∵射线OM平分∠AOC,∴∠AOC=40°×2=80°,∴∠BOD=∠AOC=80°.
故答案为:80°.
三、解答题
25、已知道四点A、B、C、D,按要求画图.
(1)画直线AB、CD交于E点;
(2)画线段AC、BD交于点F;
(3)作射线BC.
解:(1)
(2)
(3)
26、如图,线段AB=8
cm,C是线段AB上一点,AC=3.2
cm,M是AB的中点,N是AC的中点,
求线段MN的长.
解:由AB=8,M是AB的中点,所以AM=4,
又AC=3.2,所以CM=0.8cm;
因为N是AC的中点,所以NC=1.6,
所以MN=NC+CM=2.4cm.
27、如图:A、B、C、D四点在同一直线上.
(1)若AB=CD.
①比较线段的大小:AC
BD(填“>”、“=”或“<”);
②若BC=AC,且AC=12cm,则AD的长为
cm;
(2)若线段AD被点B、C分成了3:4:5三部分,且AB的中点M和CD的中点N之间的距离是16cm,求AD的长.
解:(1)①∵AB=CD,∴AB+BC=CD+BC,即,AC=BD,故答案为:=;
②∵BC=AC,且AC=12cm,∴BC=×12=9(cm),
∴AB=CD=AC﹣BC=12﹣9=3(cm),∴AD=AC+CD=12+3=15(cm),故答案为:15;
(2)如图,
设每份为x,则AB=3x,BC=4x,CD=5x,AD=12x,
∵M是AB的中点,点N是CD的中点N,∴AM=BM=x,CN=DN=x,
又∵MN=16,
∴x+4x+x=16,
解得,x=2,
∴AD=12x=24(cm),
答:AD的长为24cm.
28、如图,点O是直线FA上一点,OB,OD,OC,OE是射线,OE平分∠AOC,OD平分∠BOC.
(1)若∠AOE=15°,求∠FOC的度数;
(2)若∠AOB=86°,求∠DOE的度数.
解:(1)∵∠AOE=15°,OE平分∠AOC,∴∠AOC=2×15°=30°,
∵点O是直线FA上一点,∴∠FOC=180°﹣30°=150°.
(2)∵OE平分∠AOC,OD平分∠BOC,∴∠EOC=∠AOC,∠DOC=∠BOC,
∴∠DOE=∠AOC+∠BOC=∠AOB=×86°=43°.
29、定义:从一个角的顶点出发,把这个角分成1:2的两个角的射线,叫做这个角的三分线,显然,一个角的三分线有两条,例如:如图1,若,则OC是的一条三分线.
已知:如图是的一条三分线,且,若,求的度数.
已知:,如图2,若是的两条三分线.
求的度数.
现以O为中心,将顺时针旋转n度得到,当OA恰好是的三分线时,
求n的值.
解:如图是的一条三分线,且,,
又,;
如图是的两条三分线,;
分两种情况:
当OA是的三分线,且
∠AOC{{'}}'/>时,,
,;
当OA是的三分线,且时,,
,;
综上所述,或.??
30、如图,直线AB,CD交于点O,OE平分∠COB,OF是∠EOD的角平分线.
(1)说明:∠AOD=2∠COE;
(2)若∠AOC=50°,求∠EOF的度数;
(3)若∠BOF=15°,求∠AOC的度数.
【解析】(1)∵OE平分∠COB,∴∠COE∠COB,
∵∠AOD=∠COB,∴∠AOD=2∠COE;
(2)∵∠AOC=50°,∴∠BOC=180°﹣50°=130°,∴∠EOC∠BOC=65°,
∴∠DOE=180°﹣∠EOC=180°﹣65°=115°,
∵OF平分∠DOE,∴∠EOF∠DOC=57.5°;
(3)设∠AOC=∠BOD=α,则∠DOF=α+15°,∴∠EOF=∠DOF=α+15°,
∴∠EOB=∠EOF+∠BOF=α+30°,∴∠COB=2∠EOB=2α+60°,
而∠COB+∠BOD=180°,即,3α+60°=180°,解得,α=40°,即,∠AOC=40°.
31、已知,如图,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数.
(2)若∠MOC=m°,则∠BON的度数为
.
(3)由(1)和(2),我们发现∠MOC和∠BON之间有什么样的数量关系?
(4)若将三角形MON绕点O旋转到如图2所示的位置,试问∠MOC和∠BON之间的数量关系是否发生变化?请说明理由.
【解析】(1)如图1,∵∠MOC=28°,∠MON=90°,∴∠NOC=90°﹣28°=62°,
又∵OC平分∠AON,∴∠AOC=∠NOC=62°,
∴∠BON=180°﹣2∠NOC=180°﹣62°×2=56°,
(2)如图1,∵∠MOC=m°,∠MON=90°,∴∠NOC=90°﹣m°=(90﹣m)°,
又∵OC平分∠AON,∴∠AOC=∠NOC=(90﹣m)°,
∴∠BON=180°﹣2∠NOC=180°﹣(90﹣m)°×2=2m°,
故答案为2m°;
(3)由(1)和(2)可得:∠BON=2∠MOC;
(4)∠MOC和∠BON之间的数量关系不发生变化,
如图2,∵OC平分∠AON,∴∠AOC=∠NOC,
∵∠MON=90°,∴∠AOC=∠NOC=90°﹣∠MOC,
∴∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC,
即:∴∠BON=2∠MOC.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
