江苏省常州市“教学研究合作联盟”2020-2021学年高二上学期期中考试 数学 Word版含答案
文档属性
| 名称 | 江苏省常州市“教学研究合作联盟”2020-2021学年高二上学期期中考试 数学 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览




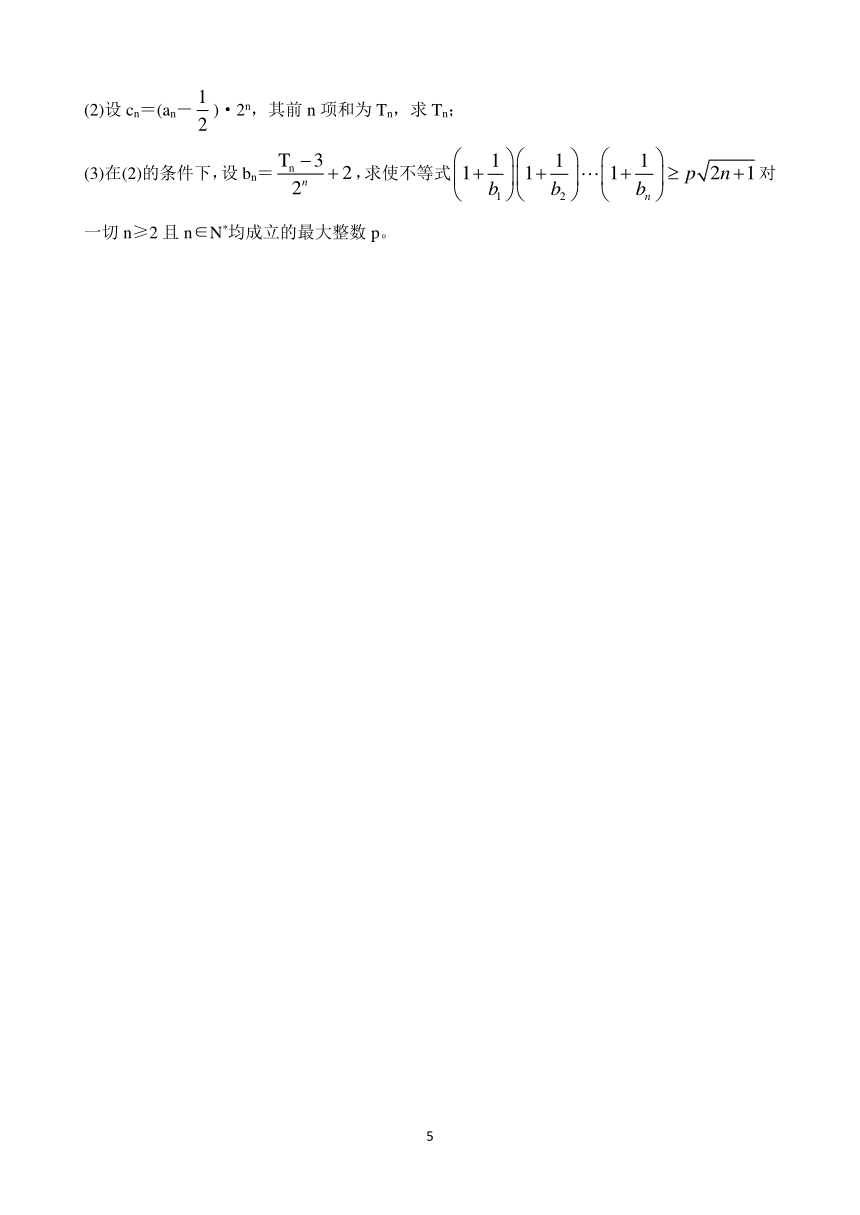
文档简介
常州市“教学研究合作联盟”
2020学年度第一学期期中质量调研
高二年级 数学试题
2020年11月
一、单项选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中只有一项符合题目要求。
1.“x>0,2x>sinx”的否定是
A.x>0,2x0,2x≤sinx
C.x0≤0,2x≤sinx0 D.x0>0,2x0≤sinx0
2.不等式≥0的解集为
A.(-∞,-3]∪[5,+∞) B.[-3,5] C.(-∞,-3)∪[5,+∞) D.(-3,5]
3.设a∈R,则“a<1”是“a2<1”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要
4.观察数列1,ln2,sin3,4,ln5,sin6,7,ln8,sin9……则该数列的第23项等于
A.sin21 B.ln20 C.sin24 D.ln23
5.《算法统宗》是中国古代数学名著,由明代数学家程大位编著,它对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著,在这部著作中,许多数学问题都是以歌诀形式呈现的.“九儿问甲歌”就是其中一首:一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百一十六,借问大儿多少岁,各儿岁数要谁推。这位公公年龄最大的儿子年龄为
A.9岁 B.12岁 C.21岁 D.36岁
6.不等式(a2-9)x2+(a+3)x-1≥0的解集是空集,则实数a的范围为
A.(-3,) B.[-3,) C.[-3,] D.[-3,)∪{3}
7.己知实数a,b满足ab>0,则的最大值为
A. B. C. D.
8.已知函数f(x)=x-+ln,若 ,其中b>0,则的最小值为
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分。在每小题给出的选项中有多项符合要求。全部选对的得5分,部分选对的得3分,有选错的得0分。
9.如果aA. B.ac2ab>b2
10.已知a∈Z,关于x的一元二次不等式x2-2x+a≤0的解集中有且仅有3个整数,则a的值可以是
A.-3 B.-2 C.-1 D.0
11.已知数列{an}为等差数列,其前n项和为Sn,且2a1+4a3=S7,则以下结论正确的有
A.a14=0 B.S14最小 C.S11=S16 D.S27=0
12.将n2(n≥3)个数排成n行n列的一个数阵,如下图:
该数阵第一列的n个数从上到下构成以m为公差的等差数列,每一行的n个数从左到右构成以m为公比的等比数列(其中m>0)。已知a11=3,a61=a13+1,记这n2个数的和为S。下列结论正确的有
A.m=2 B.a67=13×27 C.aij=(2i+1)×2j-1 D.S=n(n+2)(2n-1)
三、填空题:本大题共4小题,每小题5分,共20分,第16题第一空2分,第二空3分。
13.已知不等式x2-5ax+b>0的解集为{x|x<1或x>4},则a-b= 。
14.已知数列{an}为等差数列,Sn为{an}的前n项和,若1≤a2≤3,2≤a3≤4,则S4的取值范围是 。
15.已知x>0,y>0且xy-x+2y=6,若x+y>m2-m+1恒成立,则非零整数m的取值集合是 。
16.对于数列{an},若任意m,n∈N*(m≠n),都有≥t(t为常数)成立,则称数列{an}具有性质p(t)。
(1)若数列{an}的通项公式为an=3n,且具有性质p(t),则t的最大值为 ;
(2)若数列{an}的通项公式为an=n-,且具有性质p(9),则实数a的取值范围是 。
四、解答题:本大题共6小题共70分。解答时应写出必要的文字说明、证明过程或演算步骤。
17.(本小题满分10分)
已知集合A={x|x2-8ax+12a2>0},其中a>0;集合B={x|(x-1)(2-x)≥0}。
(1)若a=1,求A∩B;
(2)若p:x∈A,q:x∈B,且p是q的必要不充分条件,求实数a的取值范围。
18.(本小题满分10分)
已知等差数列{an}的前n项和为Sn,{bn}是各项均为正数的等比数列,a1=b4, ,b2=8,b1-3b3=4,是否存在正整数k,使得数列{}的前k项和Tk>,若存在,求出k的最小值;若不存在,说明理由。
从①S4=20,②S3=2a3,③3a3-a4=b2这三个条件中任选一个补充到上面问题中并作答。
(注:如果选择多个条件分别解答,按第一个解答计分。)
19.(本小题满分12分)
已知函数f(x)=(a,b为常数)。
(1)若b=1,解关于x的不等式f(x-2)<0;
(2)若a=2,当x∈[-1,2]时,f(x)>,恒成立,求b的取值范围。
20.(本小题满分12分)
已知数列{an}的前n项和为Sn,2Sn=an+1-3n+1+2,n∈N*,且a1,a2+6,29成等差数列。
(1)求a1的值;
(2)证明:数列{}为等差数列,并求数列{an}的通项公式;
(3)设bn=log3()+1,若对任意的n∈N*,不等式bn(1+n)-λn(bn+2)-6<0恒成立,试求实数λ的取值范围。
21.(本小题满分12分)
党中央、国务院对节能减排高度重视,各地区、各部门认真贯彻党中央、国务院关于“十三五”节能减排的决策部署,把节能减排作为转换发展方式,经济提质增效,建设生态文明的重要抓手,取得重要进展。新能源汽车环保、节能、以电代油,减少排放,既符合我国国情,也代表了汽车产业发展的方向。为了响应国家节能减排的号召,2020年常州某企业计划引进新能源汽车生产设备,通过市场分析:全年需投入固定成本2500万元。每生产x(百辆)新能源汽车,需另投入成本C(x)万元,且C(x)=。由市场调研知,每辆车售价9万元,且生产的车辆当年能全部销售完。
(1)请写出2020年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=销售-成本)
(2)当2020年产量为多少百辆时,企业所获利润最大?并求出最大利润。
22.(本小题满分14分)
已知各项均为正数的数列{an}的前n项和为Sn,且满足a13+a23+…+an3=(a1+a2+…+an)2,n∈N*。
(1)求证:an2=2Sn-an;
(2)设cn=(an-)·2n,其前n项和为Tn,求Tn;
(3)在(2)的条件下,设bn=,求使不等式对一切n≥2且n∈N*均成立的最大整数p。
11
2020学年度第一学期期中质量调研
高二年级 数学试题
2020年11月
一、单项选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中只有一项符合题目要求。
1.“x>0,2x>sinx”的否定是
A.x>0,2x
C.x0≤0,2x≤sinx0 D.x0>0,2x0≤sinx0
2.不等式≥0的解集为
A.(-∞,-3]∪[5,+∞) B.[-3,5] C.(-∞,-3)∪[5,+∞) D.(-3,5]
3.设a∈R,则“a<1”是“a2<1”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要
4.观察数列1,ln2,sin3,4,ln5,sin6,7,ln8,sin9……则该数列的第23项等于
A.sin21 B.ln20 C.sin24 D.ln23
5.《算法统宗》是中国古代数学名著,由明代数学家程大位编著,它对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著,在这部著作中,许多数学问题都是以歌诀形式呈现的.“九儿问甲歌”就是其中一首:一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百一十六,借问大儿多少岁,各儿岁数要谁推。这位公公年龄最大的儿子年龄为
A.9岁 B.12岁 C.21岁 D.36岁
6.不等式(a2-9)x2+(a+3)x-1≥0的解集是空集,则实数a的范围为
A.(-3,) B.[-3,) C.[-3,] D.[-3,)∪{3}
7.己知实数a,b满足ab>0,则的最大值为
A. B. C. D.
8.已知函数f(x)=x-+ln,若 ,其中b>0,则的最小值为
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分。在每小题给出的选项中有多项符合要求。全部选对的得5分,部分选对的得3分,有选错的得0分。
9.如果a
10.已知a∈Z,关于x的一元二次不等式x2-2x+a≤0的解集中有且仅有3个整数,则a的值可以是
A.-3 B.-2 C.-1 D.0
11.已知数列{an}为等差数列,其前n项和为Sn,且2a1+4a3=S7,则以下结论正确的有
A.a14=0 B.S14最小 C.S11=S16 D.S27=0
12.将n2(n≥3)个数排成n行n列的一个数阵,如下图:
该数阵第一列的n个数从上到下构成以m为公差的等差数列,每一行的n个数从左到右构成以m为公比的等比数列(其中m>0)。已知a11=3,a61=a13+1,记这n2个数的和为S。下列结论正确的有
A.m=2 B.a67=13×27 C.aij=(2i+1)×2j-1 D.S=n(n+2)(2n-1)
三、填空题:本大题共4小题,每小题5分,共20分,第16题第一空2分,第二空3分。
13.已知不等式x2-5ax+b>0的解集为{x|x<1或x>4},则a-b= 。
14.已知数列{an}为等差数列,Sn为{an}的前n项和,若1≤a2≤3,2≤a3≤4,则S4的取值范围是 。
15.已知x>0,y>0且xy-x+2y=6,若x+y>m2-m+1恒成立,则非零整数m的取值集合是 。
16.对于数列{an},若任意m,n∈N*(m≠n),都有≥t(t为常数)成立,则称数列{an}具有性质p(t)。
(1)若数列{an}的通项公式为an=3n,且具有性质p(t),则t的最大值为 ;
(2)若数列{an}的通项公式为an=n-,且具有性质p(9),则实数a的取值范围是 。
四、解答题:本大题共6小题共70分。解答时应写出必要的文字说明、证明过程或演算步骤。
17.(本小题满分10分)
已知集合A={x|x2-8ax+12a2>0},其中a>0;集合B={x|(x-1)(2-x)≥0}。
(1)若a=1,求A∩B;
(2)若p:x∈A,q:x∈B,且p是q的必要不充分条件,求实数a的取值范围。
18.(本小题满分10分)
已知等差数列{an}的前n项和为Sn,{bn}是各项均为正数的等比数列,a1=b4, ,b2=8,b1-3b3=4,是否存在正整数k,使得数列{}的前k项和Tk>,若存在,求出k的最小值;若不存在,说明理由。
从①S4=20,②S3=2a3,③3a3-a4=b2这三个条件中任选一个补充到上面问题中并作答。
(注:如果选择多个条件分别解答,按第一个解答计分。)
19.(本小题满分12分)
已知函数f(x)=(a,b为常数)。
(1)若b=1,解关于x的不等式f(x-2)<0;
(2)若a=2,当x∈[-1,2]时,f(x)>,恒成立,求b的取值范围。
20.(本小题满分12分)
已知数列{an}的前n项和为Sn,2Sn=an+1-3n+1+2,n∈N*,且a1,a2+6,29成等差数列。
(1)求a1的值;
(2)证明:数列{}为等差数列,并求数列{an}的通项公式;
(3)设bn=log3()+1,若对任意的n∈N*,不等式bn(1+n)-λn(bn+2)-6<0恒成立,试求实数λ的取值范围。
21.(本小题满分12分)
党中央、国务院对节能减排高度重视,各地区、各部门认真贯彻党中央、国务院关于“十三五”节能减排的决策部署,把节能减排作为转换发展方式,经济提质增效,建设生态文明的重要抓手,取得重要进展。新能源汽车环保、节能、以电代油,减少排放,既符合我国国情,也代表了汽车产业发展的方向。为了响应国家节能减排的号召,2020年常州某企业计划引进新能源汽车生产设备,通过市场分析:全年需投入固定成本2500万元。每生产x(百辆)新能源汽车,需另投入成本C(x)万元,且C(x)=。由市场调研知,每辆车售价9万元,且生产的车辆当年能全部销售完。
(1)请写出2020年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=销售-成本)
(2)当2020年产量为多少百辆时,企业所获利润最大?并求出最大利润。
22.(本小题满分14分)
已知各项均为正数的数列{an}的前n项和为Sn,且满足a13+a23+…+an3=(a1+a2+…+an)2,n∈N*。
(1)求证:an2=2Sn-an;
(2)设cn=(an-)·2n,其前n项和为Tn,求Tn;
(3)在(2)的条件下,设bn=,求使不等式对一切n≥2且n∈N*均成立的最大整数p。
11
同课章节目录
