12.1 轴对称——线段垂直平分线的性质
文档属性
| 名称 | 12.1 轴对称——线段垂直平分线的性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-08 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
12.1 轴对称(二)
——线段垂直平分线的性质
人教版初中数学
八年级上册十二章第一节
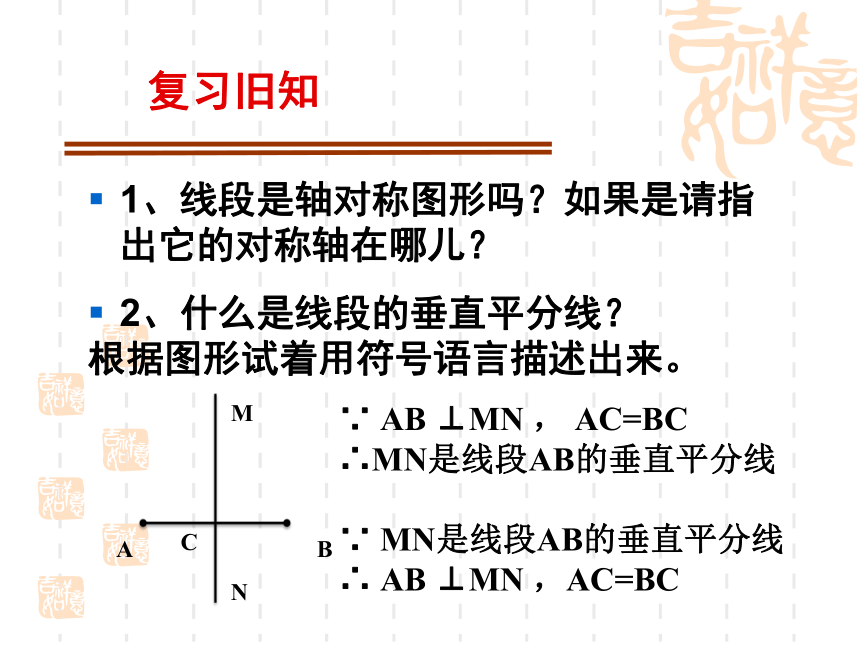
复习旧知
1、线段是轴对称图形吗?如果是请指 出它的对称轴在哪儿?
2、什么是线段的垂直平分线?
根据图形试着用符号语言描述出来。
A
B
M
N
C
∵ AB ⊥MN , AC=BC
∴MN是线段AB的垂直平分线
∵ MN是线段AB的垂直平分线
∴ AB ⊥MN ,AC=BC
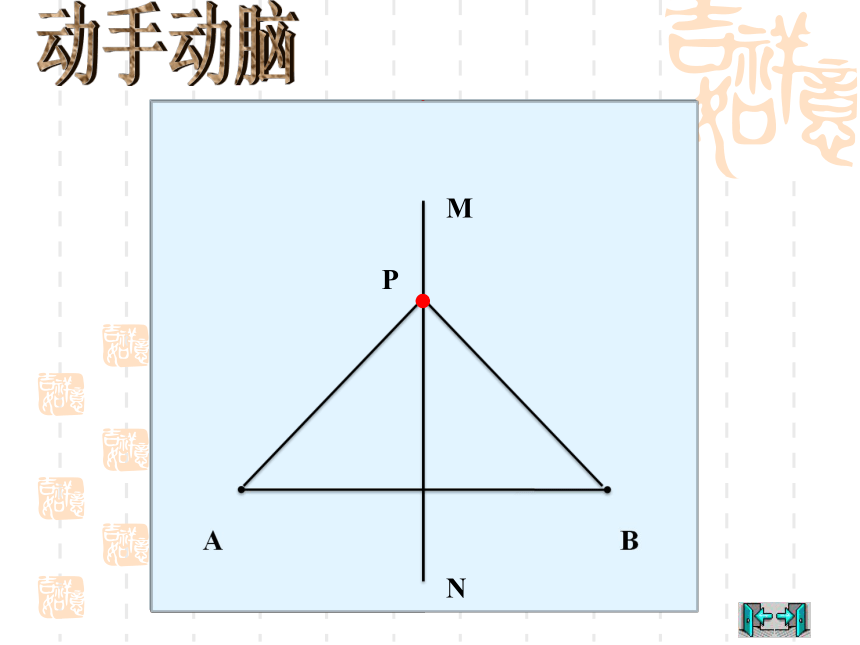
在一张纸上任意画一条线段AB
将纸对折,使线段端点A,B重合
把纸展开,并画出折痕所在直线MN
在MN上任取一点P,分别连接PA,PB
将纸沿着MN对折,观察PA和PB,有什么现象?
(B)
A
B
N
M
P
在一张纸上任意画一条线段AB
将纸对折,使线段端点A,B重合
把纸展开,并画出折痕所在直线MN
在MN上任取一点P,分别连接PA,PB
将纸沿着MN对折,观察PA和PB,有什么现象?
结论:线段垂直平分线上的点与这条线段两个端点的距离相等.
我们已经利用折纸的方法得到:
线段垂直平分线上的点与这条线段两个端点的距离相等.
你能证明这一结论吗
回顾 思考
题设:
一个点在线段的垂直平分线上
结论:
这个点与这条线段两个端点距离相等
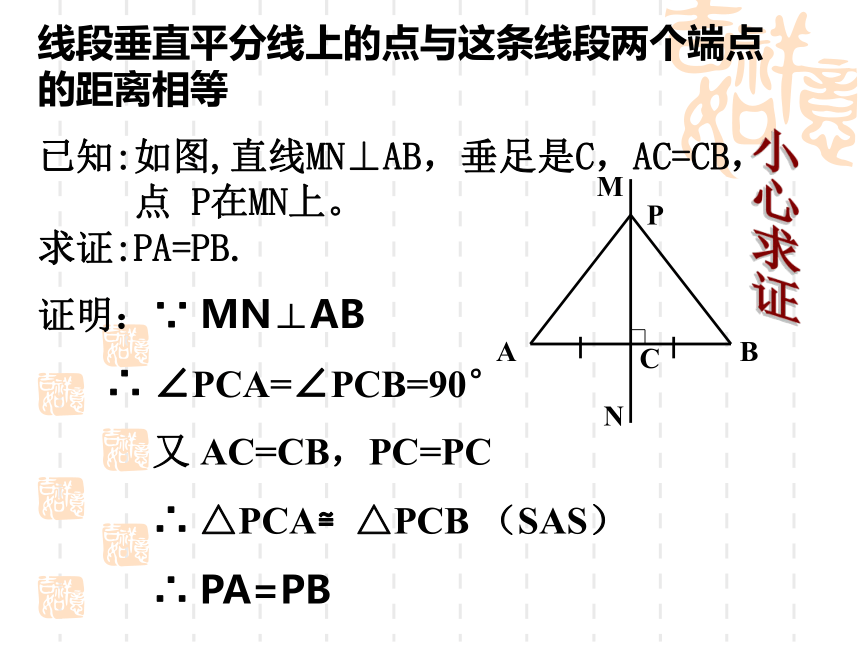
已知:如图,直线MN⊥AB,垂足是C,AC=CB,
点 P在MN上。
求证:PA=PB.
证明:∵ MN⊥AB
∴ ∠PCA=∠PCB=90°
又 AC=CB,PC=PC
∴ △PCA≌△PCB (SAS)
∴ PA=PB
A
C
B
P
M
N
线段垂直平分线上的点与这条线段两个端点的距离相等
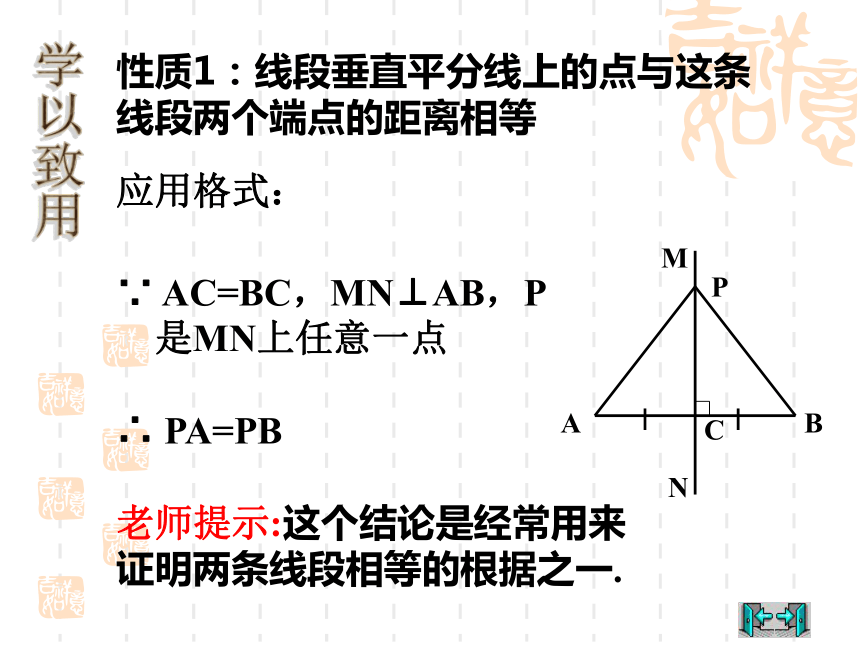
性质1:线段垂直平分线上的点与这条线段两个端点的距离相等
应用格式:
∵ AC=BC,MN⊥AB,P
是MN上任意一点
∴ PA=PB
老师提示:这个结论是经常用来证明两条线段相等的根据之一.
A
C
B
P
M
N
′
驶向胜利的彼岸
思考分析
请将命题:“线段垂直平分线上的点到这条线段两个端点距离相等”的题设、结论互换位置,并试着用语言描述出来
命题 :与一条线段两个端点距离相等的点在这条线段的垂直平分线上.
它是真命题吗 如果是,请试着证明它。
已知: 如图, PA=PB
求证: 点P在线段AB的垂直平分线上。
证明:如图,做PC⊥AB,垂足是C
∴ ∠PCA=∠PCB=90°
又 PA=PB,PC=PC
∴ Rt△PCA≌Rt△PCB (HL)
∴ AC=BC
∴ PC是线段AB的垂直平分线
即,点P在线段AB的垂直平分线上
C
B
A
P
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
性质2:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
应用格式:
∵ PA=PB
∴ 点P在AB的垂直平分线
上
老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
A
C
B
P
智勇大闯关
判断下列说法是否正确:
①若直线PE是线段AB的垂直平分线,垂足为E,则EA=EB,PA=PB;
②若PA=PB,EA=EB,则PE是线段AB的垂直平分线;
③若PA=PB,则点P必在线段AB的垂直平分线上;
④若PA=PB,则过点P的直线是线段AB的垂直平分线.
B
A
E
P
√
√
√
×
关卡一:
驶向胜利的彼岸
如图,已知AB是线段CD的垂直平分线,E是垂足,F是AB上的一点,如果EC=3cm,FC=7cm,那么ED= cm,FD= cm。
老师期望:
你能说出填空结果的根据.
7
F
D
A
B
C
E
3
关卡二:
已知:如图,AB=AC=12 cm,
AB的垂直平分线分别交AC、AB
于D、E,△ABD的周长等于29
cm,求DC的长.
A
B
C
D
E
1、 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC 、CE 的长度有什么关系?AB+BD 与DE有什么关系?
2、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
(第1题图)
(第2题图)
必做: 1. 课本 P37 习题12.1 5题
2. 同步学习 P25基础自测
3. 预习课本 P34-35
选作: 1. 课本 P38 习题12.1 12题
2.同步学习 P25拓展提高
12.1 轴对称(二)
——线段垂直平分线的性质
人教版初中数学
八年级上册十二章第一节
复习旧知
1、线段是轴对称图形吗?如果是请指 出它的对称轴在哪儿?
2、什么是线段的垂直平分线?
根据图形试着用符号语言描述出来。
A
B
M
N
C
∵ AB ⊥MN , AC=BC
∴MN是线段AB的垂直平分线
∵ MN是线段AB的垂直平分线
∴ AB ⊥MN ,AC=BC
在一张纸上任意画一条线段AB
将纸对折,使线段端点A,B重合
把纸展开,并画出折痕所在直线MN
在MN上任取一点P,分别连接PA,PB
将纸沿着MN对折,观察PA和PB,有什么现象?
(B)
A
B
N
M
P
在一张纸上任意画一条线段AB
将纸对折,使线段端点A,B重合
把纸展开,并画出折痕所在直线MN
在MN上任取一点P,分别连接PA,PB
将纸沿着MN对折,观察PA和PB,有什么现象?
结论:线段垂直平分线上的点与这条线段两个端点的距离相等.
我们已经利用折纸的方法得到:
线段垂直平分线上的点与这条线段两个端点的距离相等.
你能证明这一结论吗
回顾 思考
题设:
一个点在线段的垂直平分线上
结论:
这个点与这条线段两个端点距离相等
已知:如图,直线MN⊥AB,垂足是C,AC=CB,
点 P在MN上。
求证:PA=PB.
证明:∵ MN⊥AB
∴ ∠PCA=∠PCB=90°
又 AC=CB,PC=PC
∴ △PCA≌△PCB (SAS)
∴ PA=PB
A
C
B
P
M
N
线段垂直平分线上的点与这条线段两个端点的距离相等
性质1:线段垂直平分线上的点与这条线段两个端点的距离相等
应用格式:
∵ AC=BC,MN⊥AB,P
是MN上任意一点
∴ PA=PB
老师提示:这个结论是经常用来证明两条线段相等的根据之一.
A
C
B
P
M
N
′
驶向胜利的彼岸
思考分析
请将命题:“线段垂直平分线上的点到这条线段两个端点距离相等”的题设、结论互换位置,并试着用语言描述出来
命题 :与一条线段两个端点距离相等的点在这条线段的垂直平分线上.
它是真命题吗 如果是,请试着证明它。
已知: 如图, PA=PB
求证: 点P在线段AB的垂直平分线上。
证明:如图,做PC⊥AB,垂足是C
∴ ∠PCA=∠PCB=90°
又 PA=PB,PC=PC
∴ Rt△PCA≌Rt△PCB (HL)
∴ AC=BC
∴ PC是线段AB的垂直平分线
即,点P在线段AB的垂直平分线上
C
B
A
P
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
性质2:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
应用格式:
∵ PA=PB
∴ 点P在AB的垂直平分线
上
老师提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
A
C
B
P
智勇大闯关
判断下列说法是否正确:
①若直线PE是线段AB的垂直平分线,垂足为E,则EA=EB,PA=PB;
②若PA=PB,EA=EB,则PE是线段AB的垂直平分线;
③若PA=PB,则点P必在线段AB的垂直平分线上;
④若PA=PB,则过点P的直线是线段AB的垂直平分线.
B
A
E
P
√
√
√
×
关卡一:
驶向胜利的彼岸
如图,已知AB是线段CD的垂直平分线,E是垂足,F是AB上的一点,如果EC=3cm,FC=7cm,那么ED= cm,FD= cm。
老师期望:
你能说出填空结果的根据.
7
F
D
A
B
C
E
3
关卡二:
已知:如图,AB=AC=12 cm,
AB的垂直平分线分别交AC、AB
于D、E,△ABD的周长等于29
cm,求DC的长.
A
B
C
D
E
1、 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC 、CE 的长度有什么关系?AB+BD 与DE有什么关系?
2、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
(第1题图)
(第2题图)
必做: 1. 课本 P37 习题12.1 5题
2. 同步学习 P25基础自测
3. 预习课本 P34-35
选作: 1. 课本 P38 习题12.1 12题
2.同步学习 P25拓展提高
